石油化工厂为什么要用专业防爆手机?
防爆手机之所以必须使用专业设计的产品,主要是出于安全考虑,以防止在易燃易爆环境中因手机使用不当引发爆炸事故。以下几点详细解释了使用专业化工防爆手机的必要性:

本质安全设计:顶坚专业防爆手机采用了本质安全(本安型)技术,这意味着手机的电路设计和组件能够限制能量释放,确保即使在故障状态下也不会产生足以点燃周围爆炸性气体或粉尘的火花、热能或电弧。
防止点火源产生:在化工等危险环境中,普通手机的电路短路、电火花、电池故障、高温、静电释放等因素都可能成为有效点火源。防爆手机通过特殊设计避免了这些风险,比如使用防爆锂电池,配备专门的保护电路,以及增强的机械强度来防止跌落或撞击导致的内部损坏。
通过严格认证:顶坚防爆手机需经过国家或国际相关安全机构的严格测试和认证,确保其能够在特定的爆炸性气体环境等级(如IIC级)下安全使用,持有化工防爆合格证。
耐用性和稳定性:考虑到化工环境的严苛性,防爆手机还具备高度的耐用性和稳定性,能够承受极端温度、湿度和压力变化,确保在危险环境中持续稳定工作。
特殊材料与构造:从外壳到内部零件,防爆手机均采用抗爆、防火、耐腐蚀等特殊材料,进一步降低在危险环境中的安全隐患。
功能适应性:尽管有着严格的防爆要求,现代智能化工防爆手机仍保持了强大的通信和数据处理能力,满足行业特殊需求,如一键紧急呼叫、环境监测等,确保工作人员在紧急情况下能够迅速反应。
那么普通手机是否能起到防爆作用?
普通手机并不能起到防爆作用。市面上大多数手机并非设计用于易燃易爆环境,它们没有经过特殊的防爆处理,也没有获得相应的防爆认证。在化工、煤矿、石油、天然气等存在爆炸性气体或粉尘的危险环境中使用普通手机,存在很大的安全隐患,因为手机电池、电路或机械部件可能产生的火花、静电放电或过热等情况都可能成为点燃爆炸性混合物的点火源。
为了确保安全,这些特殊环境下必须使用专为防爆设计的手机。防爆手机通过采用防爆材料、特殊电路设计、低功耗元件、加强的密封和散热结构等方法,并且经过严格的检测认证,以达到在特定爆炸危险环境中使用而不引发爆炸的目的。所以如果工作或生活环境有防爆要求,应当选择并使用经过认证的专业防爆手机。
相关文章:

石油化工厂为什么要用专业防爆手机?
防爆手机之所以必须使用专业设计的产品,主要是出于安全考虑,以防止在易燃易爆环境中因手机使用不当引发爆炸事故。以下几点详细解释了使用专业化工防爆手机的必要性: 本质安全设计:顶坚专业防爆手机采用了本质安全(本安…...

文本生成sql模型(PipableAI/pip-sql-1.3b)
安装环境 pip3 install torch torchvision torchaudio --index-url https://download.pytorch.org/whl/cu118 pip install transformers 代码 question "What are the email address, town and county of the customers who are of the least common gender?"sc…...

机器学习中的数学底蕴与设计模式
在说机器学习设计模式之前,想多说几句,在进入软件行业最初的10年,那时候耳熟能详的基本就是多线程编程,互斥同步锁,设计模式,OOA,OOP,常规数组,tree,图的数据…...

【Android面试八股文】性能优化相关面试题:如何查找CPU占用?
文章目录 一、 如何查找CPU的占用问题二、TraceView的使用关于TraceView和Android Studio的Profiler第一步、通过Android studio 打开`Android profiler`第二步、使用步骤第三步、技术说明第四步、CPU占用相关指标说明扩展阅读一、 如何查找CPU的占用问题 在Android开发中,如…...
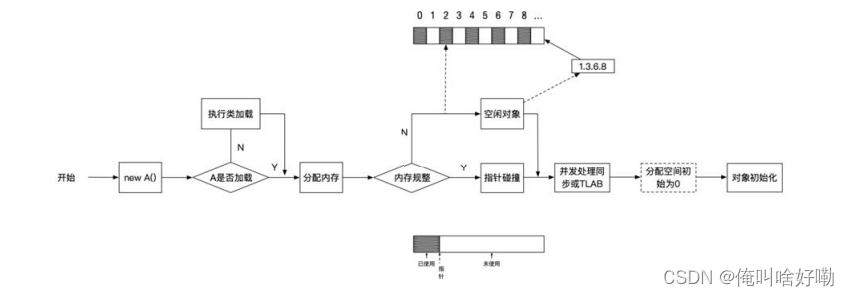
面试框架一些小结
springcloud的⼯作原理 springcloud由以下⼏个核⼼组件构成: Eureka:各个服务启动时,Eureka Client都会将服务注册到Eureka Server,并且Eureka Client还可以反过来从Eureka Server拉取注册表, 从⽽知道其他服务在哪⾥ …...

c# 往window注册表写入数据后,未写入指定的路径
c# 往window注册表写入数据后,未写入指定的路径 最近在用c#开发一个往注册表写入数据的一个项目,发现将输入写入 HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\Windows\CurrentVersion\Explorer\CommandStore\shell这个路径时,数据并没写入到这个…...
树莓派4B_OpenCv学习笔记13:OpenCv颜色追踪_程序手动调试HSV色彩空间_检测圆
今日继续学习树莓派4B 4G:(Raspberry Pi,简称RPi或RasPi) 本人所用树莓派4B 装载的系统与版本如下: 版本可用命令 (lsb_release -a) 查询: Opencv 版本是4.5.1: OpenCv颜色追踪_程序手动调试HSV色彩空间_检测灰度图中的…...

Golang | Leetcode Golang题解之第198题打家劫舍
题目: 题解: func rob(nums []int) int {if len(nums) 0 {return 0}if len(nums) 1 {return nums[0]}first : nums[0]second : max(nums[0], nums[1])for i : 2; i < len(nums); i {first, second second, max(first nums[i], second)}return se…...
)
基于ruoyi-app的手机短信登录(uniapp)
本篇用于记录h5的框架搭建 组件地址:短信验证码登陆,手机号,验证码倒计时 - DCloud 插件市场 调整后的表单组件代码: <template><view class"login-view"><!-- <input type"tel" confirm-type"确认"…...

机器学习环境搭建
前言 个人笔记,记录框架和小问题,没有太详细记载。。 1、Anaconda安装 下载地址: Free Download | Anaconda (慢) 国内镜像:https://link.csdn.net/?targethttp%3A%2F%2Fitcxy.xyz%2F241.html 下载…...
2095.删除链表的中间节点
给你一个链表的头节点 head 。删除链表的中间节点 ,并返回修改后的链表的头节点 head。 长度为 n 链表的中间节点是从头数起第 ⌊n / 2⌋ 个节点(下标从 0 开始),其中 ⌊x⌋ 表示小于或等于 x 的最大整数。 对于 n 1、2、3、4 和…...

Qt QML 坑
Qt QML 坑 QML Listview 1、不定高item 导致item重叠 ListView {id: _cityListViewproperty var _cityArray: [{ type:"A",cityArray:[]},{ type:"B",cityArray:[]},{ type:"C",cityArray:[]},{ type:"D",cityArray:[]}]model: List…...
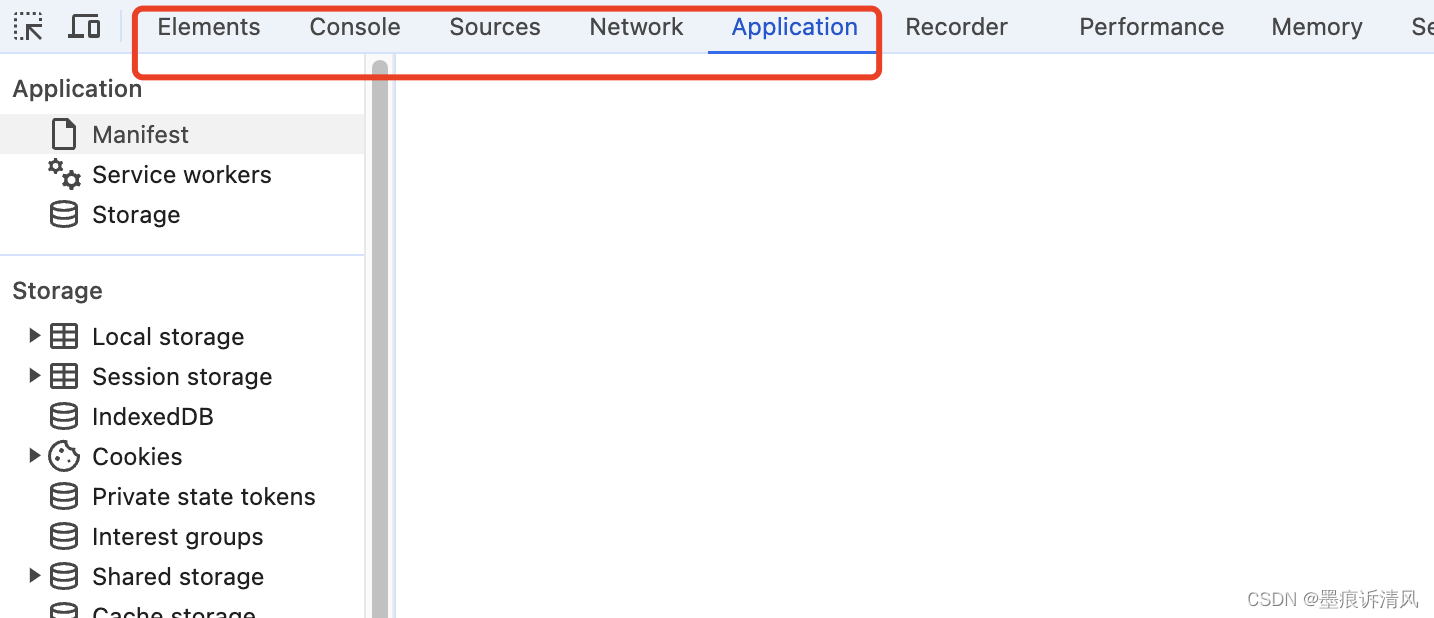
Chrome浏览器web调试(js调试、css调试、篡改前置)
目录 1. 打开开发者工具(Dev Tool) 2. 打开命令菜单 截图 3. 面板介绍 4. CSS调试 右键检查快速到达元素处 查找DOM数 利用面板Console查找DOM节点 内置函数查找上一个选择点击的元素 5. 调试JS代码(Javascript调试) 日志调试 选择查看日志等级 眼睛观测变量 …...

【Java】Logbook优化接口调用日志输出,优雅!
logbook 简介 很多人可能没有接触过 logbook,但它的确是一个很好用的日志框架。引用官网的介绍 Logbook 是一个可扩展的 Java 库,可以为不同的客户端和服务器端技术启用完整的请求和响应日志记录。它通过以下方式满足了特殊需求: 允许 Web 应…...

LabVIEW电压电流实时监测系统
开发了一种基于LabVIEW和研华(Advantech)数据采集卡的电压电流实时监测系统,通过高效的数据采集和处理,为工业和科研用户提供高精度、实时的电压电流监测解决方案。系统采用研华USB-4711A数据采集卡,结合LabVIEW编程环…...
骁龙相机拍照流程分析
和你一起终身学习,这里是程序员Android 经典好文推荐,通过阅读本文,您将收获以下知识点: 1.deliverInputEvent 拍照点击事件处理 2.submitRequestList Camera 提交拍照请求 3.createCaptureRequest 拍照请求帧数 骁龙相机通过binder 数据传输…...
sql-语句
文章目录 SQL语句的学习sql是什么sql的内置命令sql的种类sql mode库,表属性介绍:字符集,存储引擎列的数据类型:数字,字符串,时间列的约束DDL: 数据定义语言库表 Online DDL(ALGORITHM) *DML :数据操纵语言资…...

解决Vue3项目中跨域问题的步骤
决Vue3项目中跨域问题的步骤可以按照以下方式清晰地分点表示和归纳: 1. 使用代理服务器(Proxy) 步骤: 在Vue项目的根目录下找到或创建vue.config.js文件。在vue.config.js中配置devServer的proxy选项。设定需要代理的接口前缀&a…...

macos scroll direction
If there is no Trackpad option, we can change it in the Mouse option. How to Change the Scroll Direction on a Mac: 2 Ways...

Websocket实现方式二——注解方式
添加Websocket依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dependency>根据ServerEndpoint注解注册Websocket Configuration public class AgentWsConfig …...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...
