python实现符文加、解密
在历史悠久的加密技术中,恺撒密码以其简单却有效的原理闻名。通过固定的字母位移,明文可以被转换成密文,而解密则是逆向操作。这种技术不仅适用于英文字母,还可以扩展到其他语言的字符体系,如日语的平假名或汉语的拼音。本文探讨了恺撒密码的基本原理及其在实际应用中的使用案例,并用python来实现该方法。
工作中经常性会需要对一些信息进行解密,人们普遍使用一些较为简单的加密方式。加密技术不仅令人着迷,还在信息安全领域发挥着重要作用。通过深入理解这些方法,我们能更好地保护数据安全,同时也能理解历史上许多重要文献背后隐藏的秘密。恺撒密码作为加密技术的先驱,不仅启发了现代密码学的发展,也提醒我们保持对数据安全和隐私的关注。
在这篇文章中,我们将探索恺撒密码和相关字符加解密的基本原理及其在现代应用中的价值。通过python分析其加密和解密过程,我们可以更好地理解数据保护的重要性,以及加密技术如何在信息交流和安全中发挥作用。
目录
一、凯撒密码加、解密
1.1 通过位移的python实现
1.2 通过建立映射的python实现
二、函数映射加、解密
一、凯撒密码加、解密
我们首先学习通过凯撒密码进行解密。恺撒密码是一种通过将明文字母表按照固定数目进行位移来加密的方法。此加密技术不仅适用于英文字母,也可以应用于其他字符体系,如日语中的平假名或汉语拼音。
如下图所示我们用小写的英文字母表示明文,用大写英文字母表示密文,并对字母表平移三位字母方式进行加密。此处我们需要对KHOORLDPDSROLFHRIILFHUSOHDVHVKRZPHBRXULGHQWLILFDWLRQGRFXPHQWV 这段密文进行解密,并将解密后的信息写入同目录caesar.txt文件中。

1.1 通过位移的python实现
# 定义一个名为 decrypt 的函数,该函数接收两个参数:ciphertext(密文)和 shift(位移量)
def decrypt(ciphertext, shift):# 初始化一个空字符串 plaintext,用于存储解密后的明文plaintext = ""# 遍历密文中的每个字符for char in ciphertext:# 判断字符是否为大写英文字母if 'A' <= char <= 'Z':# 对大写英文字母进行解密操作,ord(char) 获取字符的 ASCII 码值,ord('A') 是字母 A 的 ASCII 码值# (ord(char) - ord('A') - shift) 计算字符在字母表中的相对位置并减去位移量# % 26 确保结果仍在 26 个英文字母的范围内# chr(...) 将计算后的 ASCII 码值转换回字符decrypted_char = chr((ord(char) - ord('A') - shift) % 26 + ord('A'))# .lower() 将解密后的大写字母转换为小写plaintext += decrypted_char.lower() # 转换为小写else:# 如果字符不是大写英文字母,则直接添加到 plaintext 字符串中plaintext += charreturn plaintext# 给定的密文
ciphertext = "KHOORLDPDSROLFHRIILFHUSOHDVHVKRZPHBRXULGHQWLILFDWLRQGRFXPHQWV"# 解密密文,假设密文是通过向后平移3位加密的
shift = 3
decrypted_text = decrypt(ciphertext, shift)
print("明文信息为:", decrypted_text)# 将解密后的文本写入文件
file_path = './caesar.txt'with open(file_path, 'w') as file:file.write(decrypted_text)1.2 通过建立映射的python实现
list_c = {'A':'x','B':'y','C':'z','D':'a','E':'b','F':'c','G':'d','H':'e','I':'f','J':'g','K':'h','L':'i','M':'j','N':'k','O':'l','P':'m','Q':'n','R':'o','S':'p','T':'q','U':'r','V':'s','W':'t','X':'u','Y':'v','Z':'w'}# 给定的密文
ciphertext = "KHOORLDPDSROLFHRIILFHUSOHDVHVKRZPHBRXULGHQWLILFDWLRQGRFXPHQWV"# 解密密文
print("明文信息为:",ciphertext)
plaintext = ""
for char in list(ciphertext):print(list_c[char])plaintext += str(list_c[char])# plaintext += list_c[char]
print("加密信息为:",plaintext)
# 将解密后的文本写入文件
file_path = './caesar.txt'with open(file_path, 'w') as file:
file.write(plaintext)打印结果:
明文信息为: KHOORLDPDSROLFHRIILFHUSOHDVHVKRZPHBRXULGHQWLILFDWLRQGRFXPHQWV
加密信息为: helloiamapoliceofficerpleaseshowmeyouridentificationdocuments
二、函数映射加、解密
这张图片展示了两个加密和解密的字符串,分别使用了不同的字母替换方法。第一个字符串使用了一种特定的字母排列方式来隐藏信息,而第二个字符串则显示了如何通过相同的排列方式来解密。
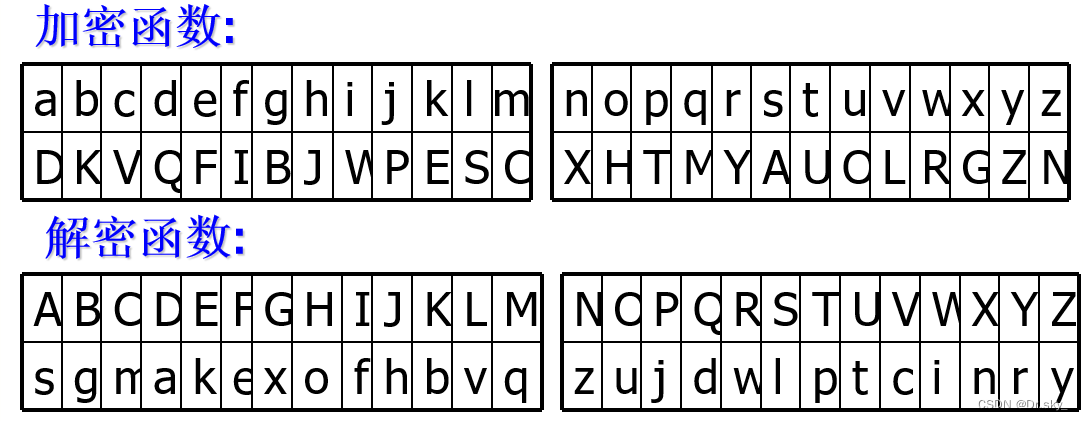
使用python实现映射关系
list_c = {'a':'D','b':'K','c':'V','d':'Q','e':'F','f':'I','g':'B','h':'J','i':'W','j':'P','k':'E','l':'S','m':'C','n':'X','o':'H','p':'T','q':'M','r':'Y','s':'A','t':'U','u':'O','v':'L','w':'R','x':'G','y':'Z','z':'N'}# 给定的密文
ciphertext = "this is the police please stay calm"# 解密密文
print("明文信息为:",ciphertext)
plaintext = ""
for char in list(ciphertext):if char == " ":plaintext += char# print(list_c[char])else: plaintext += str(list_c[char])# plaintext += list_c[char]
print("加密信息为:",plaintext)
# 将解密后的文本写入文件
file_path = '/home/qingjiao/数据安全应用/plaintext.txt'with open(file_path, 'w') as file:
file.write(plaintext)打印结果:
明文信息为: this is the police please stay calm
加密信息为: UJWA WA UJF THSWVF TSFDAF AUDZ VDSC
相关文章:

python实现符文加、解密
在历史悠久的加密技术中,恺撒密码以其简单却有效的原理闻名。通过固定的字母位移,明文可以被转换成密文,而解密则是逆向操作。这种技术不仅适用于英文字母,还可以扩展到其他语言的字符体系,如日语的平假名或汉语的拼音…...

【解释】i.MX6ULL_IO_电气属性说明
【解释】i.MX6ULL_IO_电气属性说明 文章目录 1 Hyst1.1 迟滞(Hysteresis)是什么?1.2 GPIO的Hyst. Enable Field 参数1.3 应用场景 2 Pull / Keep Select Field2.1 PUE_0_Keeper — Keeper2.2 PUE_1_Pull — Pull2.3 选择Keeper还是Pull 3 Dr…...

02-《石莲》
石 莲 石莲(学名:Sinocrassula indica A.Berger),别名因地卡,为二年生草本植物,全株无毛,具须根。花茎高15-60厘米,直立,常被微乳头状突起。茎生叶互生,宽倒披…...
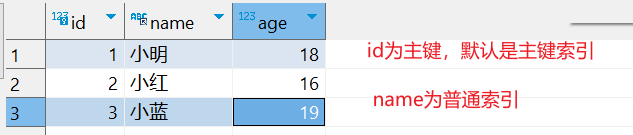
MySQL之聚簇索引和非聚簇索引
1、什么是聚簇索引和非聚簇索引? 聚簇索引,通常也叫聚集索引。 非聚簇索引,指的是二级索引。 下面看一下它们的含义: 1.1、聚集索引选取规则 如果存在主键,主键索引就是聚集索引。如果不存在主键,将使…...
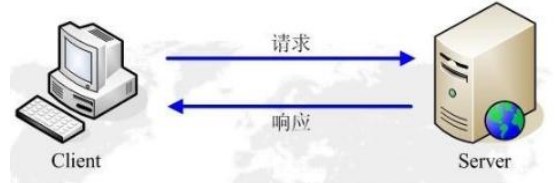
Web后端开发之前后端交互
http协议 http ● 超文本传输协议 (HyperText Transfer Protocol)服务器传输超文本到本地浏览器的传送协议 是互联网上应用最为流行的一种网络协议,用于定义客户端浏览器和服务器之间交换数据的过程。 HTTP是一个基于TCP/IP通信协议来传递数据. HTT…...

520. 检测大写字母 Easy
我们定义,在以下情况时,单词的大写用法是正确的: 全部字母都是大写,比如 "USA" 。 单词中所有字母都不是大写,比如 "leetcode" 。 如果单词不只含有一个字母,只有首字母大写࿰…...

vue的跳转传参
1、接收参数使用route,route包含路由信息,接收参数有两种方式,params和query path跳转只能使用query传参,name跳转都可以 params:获取来自动态路由的参数 query:获取来自search部分的参数 写法 path跳,query传 传参数 import { useRout…...

docker配置镜像源
1)打开 docker配置文件 sudo nano /etc/docker/daemon.json 2)添加 国内镜像源 {"registry-mirrors": ["https://akchsmlh.mirror.aliyuncs.com","https://registry.docker-cn.com","https://docker.mirrors.ustc…...
MySQL高级-SQL优化-insert优化-批量插入-手动提交事务-主键顺序插入
文章目录 1、批量插入1.1、大批量插入数据1.2、启动Linux中的mysql服务1.3、客户端连接到mysql数据库,加上参数 --local-infile1.4、查询当前会话中 local_infile 系统变量的值。1.5、开启从本地文件加载数据到服务器的功能1.6、创建表 tb_user 结构1.7、上传文件到…...
认识100种电路之振荡电路
在电子电路领域,振荡是一项至关重要的功能。那么,为什么电路中需要振荡?其背后的原理是什么?让我们一同深入探究。 【为什么需要振荡电路】 简单来说,振荡电路的存在是为了产生周期性的信号。在众多电子设备中&#…...
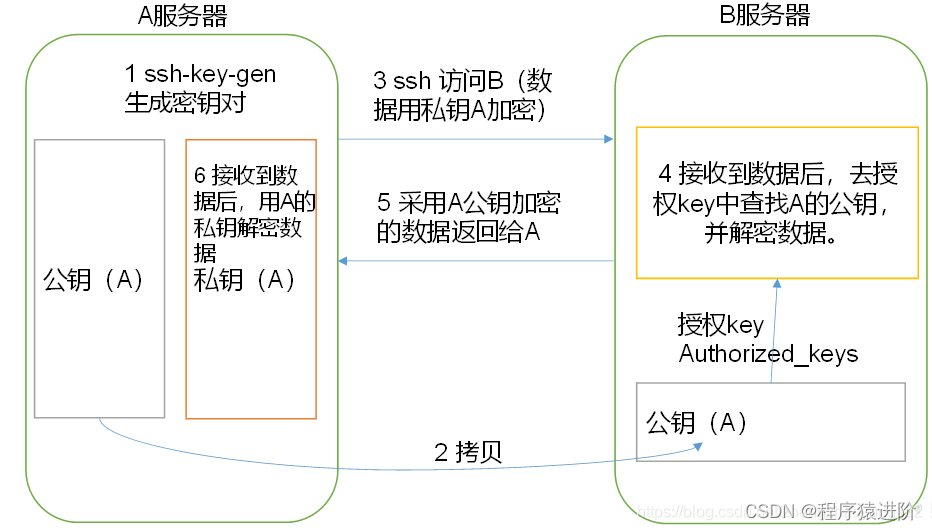
SSH 无密登录配置流程
一、免密登录原理 非对称加密: 由于对称加密的存在弊端,就产生了非对称加密,非对称加密中有两个密钥:公钥和私钥。公钥由私钥产生,但却无法推算出私钥;公钥加密后的密文,只能通过对应的私钥来解…...

Python自动化运维 系统基础信息模块
1.系统信息的收集 系统信息的收集,对于服务质量的把控,服务的监控等来说是非常重要的组成部分,甚至是核心的基础支撑部分。我们可以通过大量的核心指标数据,结合对应的检测体系,快速的发现异常现象的苗头,进…...

如何安装和配置Monit
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 关于 Monit Monit 是一个有用的程序,可以自动监控和管理服务器程序,以确保它们不仅保持在线,而且文…...

【redis】redis分片集群基础知识
1、基本概念 1.1定义 分片:数据按照某种规则(比如哈希)被分割成多个片段(或分片),每个片段被称为一个槽(slot)。槽是Redis分片集群中数据的基本单元。节点:Redis分片集…...

Python 面试【★★★★】
欢迎莅临我的博客 💝💝💝,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「stormsha的主页」…...

Knife4j 2.2.X 版本 swagger彻底禁用
官方文档配置权限:https://doc.xiaominfo.com/v2/documentation/accessControl.html#_3-5-1-%E7%94%9F%E4%BA%A7%E7%8E%AF%E5%A2%83%E5%B1%8F%E8%94%BD%E8%B5%84%E6%BA%90 通常有时候我们碰到的问题如下: 在开发Knife4j功能时,同很多开发者经常讨论的问…...

linux下mysql的定时备份
备份是容灾的基础,是指为了防止系统出现操作或系统故障导致数据丢失,而将全部或部分数据集合从应用主机的硬盘或阵列复制到其他的存储介质的过程为什么备份 硬件故障软件故障误操作病毒入侵保留历史记录灾难性事件 存储介质 光盘磁带硬盘磁盘阵列DAS:直接…...

【13】地址-比特币区块链的地址
1. 比特币区块链的地址 这就是一个真实的比特币地址:1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa。这是史上第一个比特币地址,据说属于中本聪。 比特币地址是完全公开的,如果你想要给某个人发送币,只需要知道他的地址就可以了。实际上,所谓的地址,只不过是将公钥表示成人类可读…...

【数据结构】数据结构前置知识
这里写目录标题 基本概念与术语数据数据元素数据项数据对象数据结构 逻辑结构和物理结构物理结构顺序存储结构链式存储结构 逻辑结构集合结构线性结构树形结构图形结构 算法时间复杂度和空间复杂度大O的渐进表示法时间复杂度常数阶线性阶对数阶平方阶常见时间复杂度 空间复杂度…...
企业数据挖掘平台产品特色及合作案例介绍
泰迪企业数据挖掘平台是一款通用的、企业级、智能化的数据分析模型构建与数据应用场景设计工具,能够一体化地完成数据集成、模型构建、模型发布,为数据分析、探索、服务流程提供支撑,提供完整的数据探索、多数据源接入、特征处理、模型搭建、…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
