【征服数据结构】:期末通关秘籍
【征服数据结构】:期末通关秘籍
- 💘 数据结构的基本概念
- 😈 数据结构的基本概念
- 😈 逻辑结构和存储结构的区别和联系
- 😈 算法及其特性
- 😈 简答题
- 💘 线性表(链表、单链表)
- 😈 大题1
- ❄️ 题目解析
- ❄️ 算法思想和时间复杂度
- ❄️ 代码实现
- ❄️ 某搜题软件上的答案
- 😈 大题2
- ❄️ 答案解析
- 💘 栈和队列
- 😈 大题1
- ❄️ 题目分析
- ❄️ 答案解析
- ❄️ 标准答案(取自某搜题软件)
- 😈 简答题1
- 😈 简答题2
- 💘 树
- 😈 二叉树的定义、性质和应用
- 😈 二叉树的先序、中序遍历和后序遍历
- 😈 已知遍历序列构造二叉树
- ❄️ 大题1
- 💑 二叉树如何转换成森林
- 🐸 二叉树如何转换成树
- 🐸 将二叉树如何转换成森林
- 💑 标准答案(出自某搜题软件)
- ❄️ 大题2
- 💑 答案解析
- 💑 标准答案
- ❄️ 大题3
- 💑 答案
- 💑 标准答案
- ❄️ 简答题1
- 💑 标准答案
- ❄️ 简答题2
- 💑 标准答案
- ❄️ 简答题3
- 💑 答案解析
- 💑 标准答案
- 😈 森林的先序遍历和中序遍历(可能出选择题)
- 😈 树转化为二叉树以及森林转化成二叉树
- 😈 哈夫曼树和哈弗曼编码(这里肯定会出大题)
- 😈 大题1
- ❄️ 答案解析
- 😈 线索二叉树
- 💘 图
- 😈 图的连通性问题
- 😈 出度和入度
- 😈 带权无向图的最小生成树Prim、KrusKal算法
- 😈 有向无环图、拓扑排序
- 😈 大题1
- ❄️ 答案解析
- 😈 大题2
- ❄️ 标准答案
- 😈 关键路径和关键活动
- ❄️ 大题2
- 💑 答案解析
- 💑 标准答案
- 😈 图的遍历(广度优先和深度优先)
- 😈 最短路径
- ❄️ 大题3
- 💑 答案解析
- 💑 标准答案
- 💘 查找
- 😈 静态查找表:顺序查找、折半查找
- ❄️ 大题1
- 💑 答案解析
- 💑 标准答案
- 😈 动态查找表: 二叉排序树、二叉平衡树、m阶B树
- ❄️ 二叉排序树
- ❄️ 二叉平衡树
- ❄️ 大题1
- 💑 答案解析
- 💑 标准答案
- 😈 B树
- ❄️ 大题2
- 💑 答案解析
- 😈 哈希表
- ❄️ 哈希表的长度、哈希表的装填因子等
- ❄️ 常用的构造哈希函数的方法
- ❄️ 处理冲突的方法
- ❄️ 大题3
- 💑 答案解析
前言:本篇博客只做博主复习使用,不做其它,若有问题,也欢迎大家留言反馈。所有例题均为ZZULI往年期末题,正当途径获得。最后一章排序章节较简单,博主没有单独列出。
参考&鸣谢
AVL树的插入操作(旋转)图解 MaxBruce
解决Hash(哈希表)冲突的四种方案 FrozenPenguin
图——关键路径 傅华涛Fu
拓扑排序详解 Dream of maid
生成树(基础) 莫忘、莫念
图的连通性问题 _Tham
数据结构】树、二叉树和森林的相互转换 Jacky_Feng
【专题】树和森林的遍历 ᝰꫛꪮꪮꫜ hm
💘 数据结构的基本概念
😈 数据结构的基本概念
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。—选自百度百科
😈 逻辑结构和存储结构的区别和联系


😈 算法及其特性

😈 简答题


2)

3)

💘 线性表(链表、单链表)
顺序存储结构及其基本操作:请看博主这篇博客。
链式存储结构及其基本操作:请看博主这篇博客
😈 大题1

❄️ 题目解析

❄️ 算法思想和时间复杂度
- 题目说了,需要我们释放结点的空间。
首先创建两个结点指针变量
pre,cur,让pre初始化为Head,cur初始化为Head->next,开始遍历带头单链表,分为两种情况:
- 如果
pre指针的数据域和cur指针的数据域相等,那我们就删除掉cur指针指向的结点(释放结点空间后,完成链接即可),删除cur之前,保存cur->next给变量next_,删除完之后更新cur为next_,pre不用更新,因为当前的值还可能和pre的数据域相等。- 如果
pre指针的数据域和cur指针的数据域不相等,更新这两个指针,pre更新为cur,cur更新为cur->next。最后
cur结点指针指向NULL,循环结束。
时间复杂度是 O ( l o g N ) O(logN) O(logN)。
❄️ 代码实现
void remove(LinkList Head)
{LinkList pre = Head;//前一个结点指针LinkList cur = Head->next;//后一个结点指针while (cur != NULL){if (pre->data != cur->data)//如果pre和cur的data不相等{pre = cur;cur = cur->next;}else//如果pre和cur的data相等{//先删除掉cur结点LinkList node = cur->next;//保存cur->next指针结点free(cur);//释放结点空间pre->next = node;//链接cur = node;//更新cur指针}}
}
❄️ 某搜题软件上的答案

😈 大题2

❄️ 答案解析
在写代码前,我们还是画图来分析以下,删除链表结点是如何删除的:
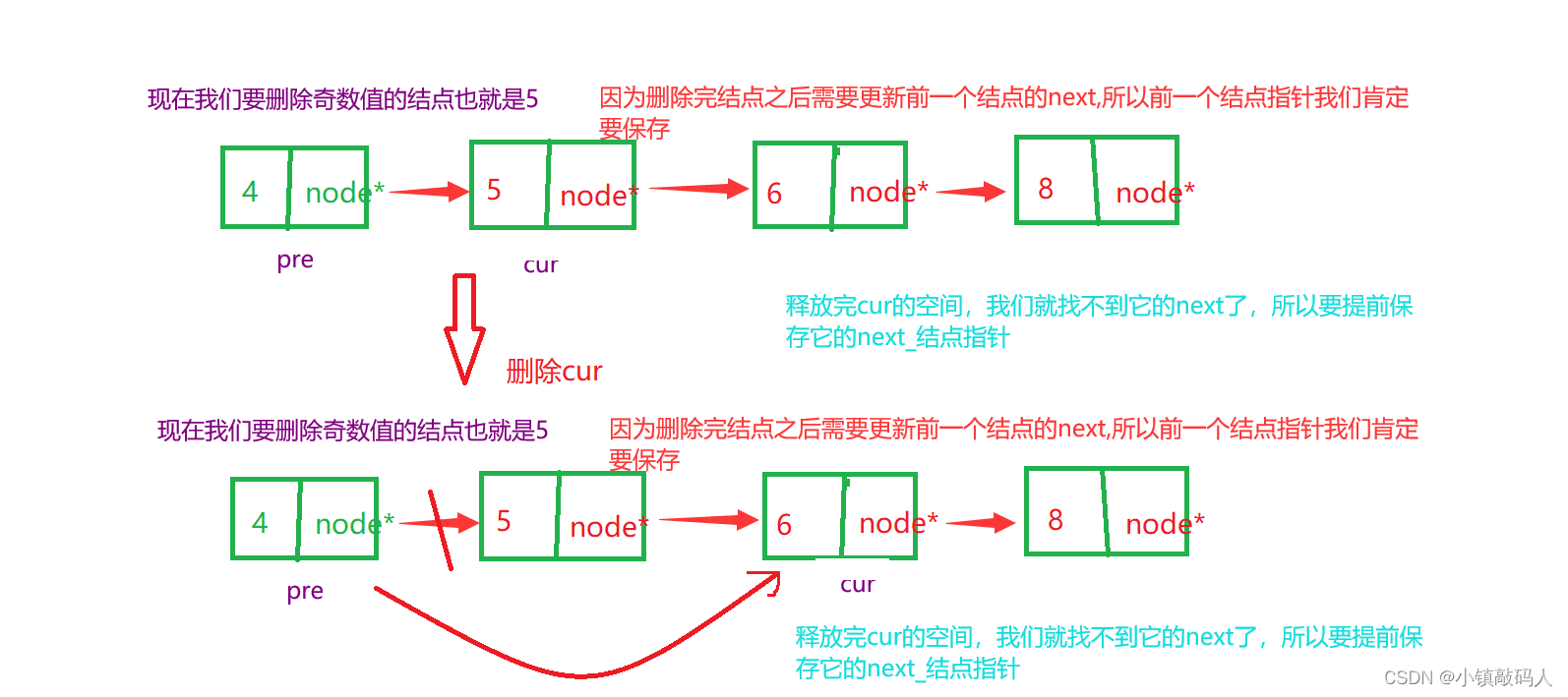
代码示例(C语言实现):
LinkList deleteodd(LinkList L)
{LinkList pre = L;//pre是当前遍历位置的前一个结点指针LinkList cur = L->next;//cur变量是当前遍历位置的结点指针while (cur != NULL)//cur为空就停止循环{if (cur->data % 2 == 0)//如果当前结点指针指向的结点的数据域是偶数,正常更新{pre = cur;cur = cur->next;}else//否则,就删除当前结点{//先保存当前结点的下一个结点指针,防止将当前结点释放后无法找到下一个结点的指针LinkList next_ = cur->next;free(cur);pre->next = next_;//更新pre的nextcur = next_;//更新cur}}return L;//返回头节点
}
💘 栈和队列
栈和队列的基本特征:栈里面的数据后进先出。队列里的数据先进先出。
它们的逻辑结构都是线性结构。可以用线性表或者单链表来实现。详细请看博主这篇博客
栈和队列作为线性结构中比较典型的两个结构(应用多),是很可能出一道大题的,下面我们来看一道大题(ZZULI往年期末题):
😈 大题1

❄️ 题目分析

上图忘记说明一点了,终态不为空也不叫满足要求,需要返回false。
❄️ 答案解析

2. 代码实现:
bool is_valid(char* s)
{int cnt_i = 0;//统计入栈的次数int cnt_o = 0;//统计出栈的次数int i = 0;while (s[i] != '\0'){if (s[i] == 'O')cnt_o++;elsecnt_i++;if (cnt_i < cnt_o){std::cout << "序列非法“ << std::endl;//用printf打印也可以return false; }i++;}if (cnt_i > cnt_o){std::cout << "序列非法“ << std::endl;//用printf打印也可以return false;}std::cout << "序列合法" << std::endl;return true;
}
上述代码应该是C++语言实现,因为C语言中没有bool这个类型。打印处使用printf也可以,因为c++语言兼容C语言。
❄️ 标准答案(取自某搜题软件)



😈 简答题1

题目让我们描述栈和队列的逻辑结构和特性,并分别举出两个应用实例。
栈和队列的逻辑结构都是线性结构,栈具有后进先出的特性,意思是后面入栈的元素,在进行出栈操作时会先出去。
队列具有先进先出的特性,意思是先入队列的元素,在进行出队列操作时,会先出去。
应用示例:栈:递归、后缀表达式求值。队列:二叉树的层次遍历、图的广度优先搜索。
😈 简答题2

- 首先来回答第一个问题
什么是循环队列?
循环队列是队列的一种,普通的队列如果采用数组的方式存储的话,为了不挪动数据,删除队列元素时,我们可能会直接将队列首元素的下标后移,这样就会造成一个问题,就是队列的空间在减少,继续入队列(尾插)如果数组的空间满了,这个时候如果进行过出队列,就会造成队列的元素小于数组实际的大小的情况。循环队列就是为了解决这种问题,让空间的利用大大提高。我们只需要把一个数组逻辑上想象成首尾相接即可。
用文字描述可能很抽象,我们画图来解释:

- 其次就是循环队列的判空和判满问题。
先说结论: front = rear时为空
(rear+1)%n = front时为满,n为数组的大小。我们画图来分析一下为什么是这样:

贴一个 标准答案:
- 在顺序队列中由于数组空间不够而产生的溢出叫真溢出;顺序队列因多次入队列和出队列操作后出现的有存储空间但不能进入队列操作的溢出称为假溢出。 假溢出是由于队尾rear的值和队头front的值不能由所定义数组下界值自动转为数组上界值而产生的。其解决办法有二一是将队列元素向前“平移”(占用0至rear-front-1);二是将队列看成首尾相连即循环队列[0…m-1]。
- 在循环队列下仍定义。front=rear时为队空而判断队满则用两种办法: 一是用“牺牲一个单元”即rear+1=front(准确记是(rear+1)%m=frontm是队列容量)时为队满。
另一种解法是“设标记”方法如设标记tag,tag等于0的情况下若删除时导致front=tear为队空;tag=1的情况下若因插入导致front=rear则为队满。
💘 树
如果你对二叉树什么都不了解,可以看博主,这篇博客
😈 二叉树的定义、性质和应用
- 定义
二叉树是一种特殊的树,它的每个结点至多有两个子树,它的子树是有顺序的,即使一个结点只有一个子树,你也要指明是左子树还是右子树。
2)性质

3)应用

😈 二叉树的先序、中序遍历和后序遍历
这里在上述博客链接里面的文章里我们也有详细的叙述,这里我们在简单的画图叙述一下:

😈 已知遍历序列构造二叉树
一般都是给一个中序遍历序列、后序和前序遍历序列给一个,让你构造二叉树。
中序遍历序列的作用是划分某个结点的左子树和右子树。
后序或者前序遍历序列的作用是确定当前根结点。
❄️ 大题1
我们通过题目来讲解
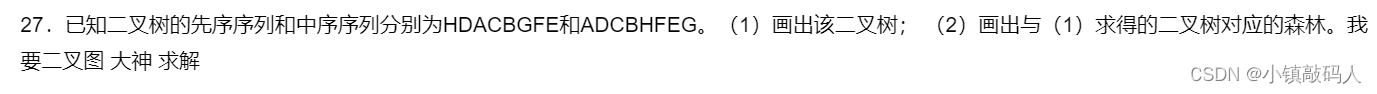
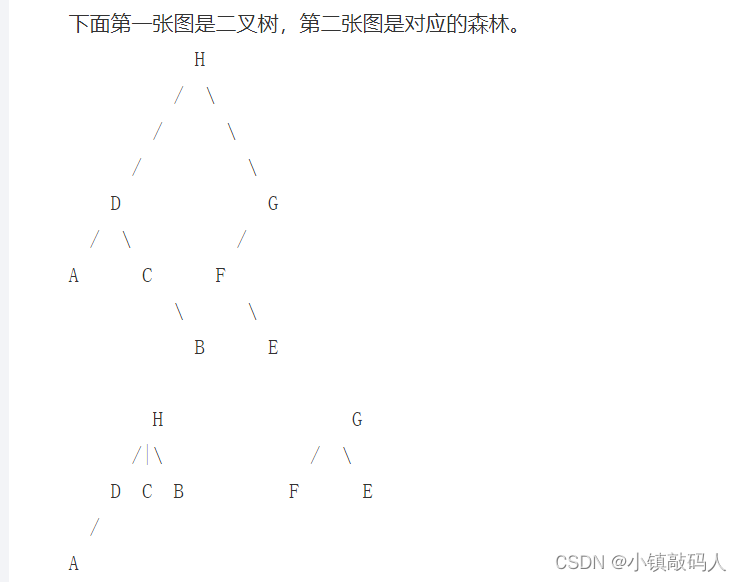
💑 二叉树如何转换成森林
🐸 二叉树如何转换成树
要学会二叉树转换成森林,我们首先要学会将一棵二叉树转化成树。
我们画图来详细说明其步骤:
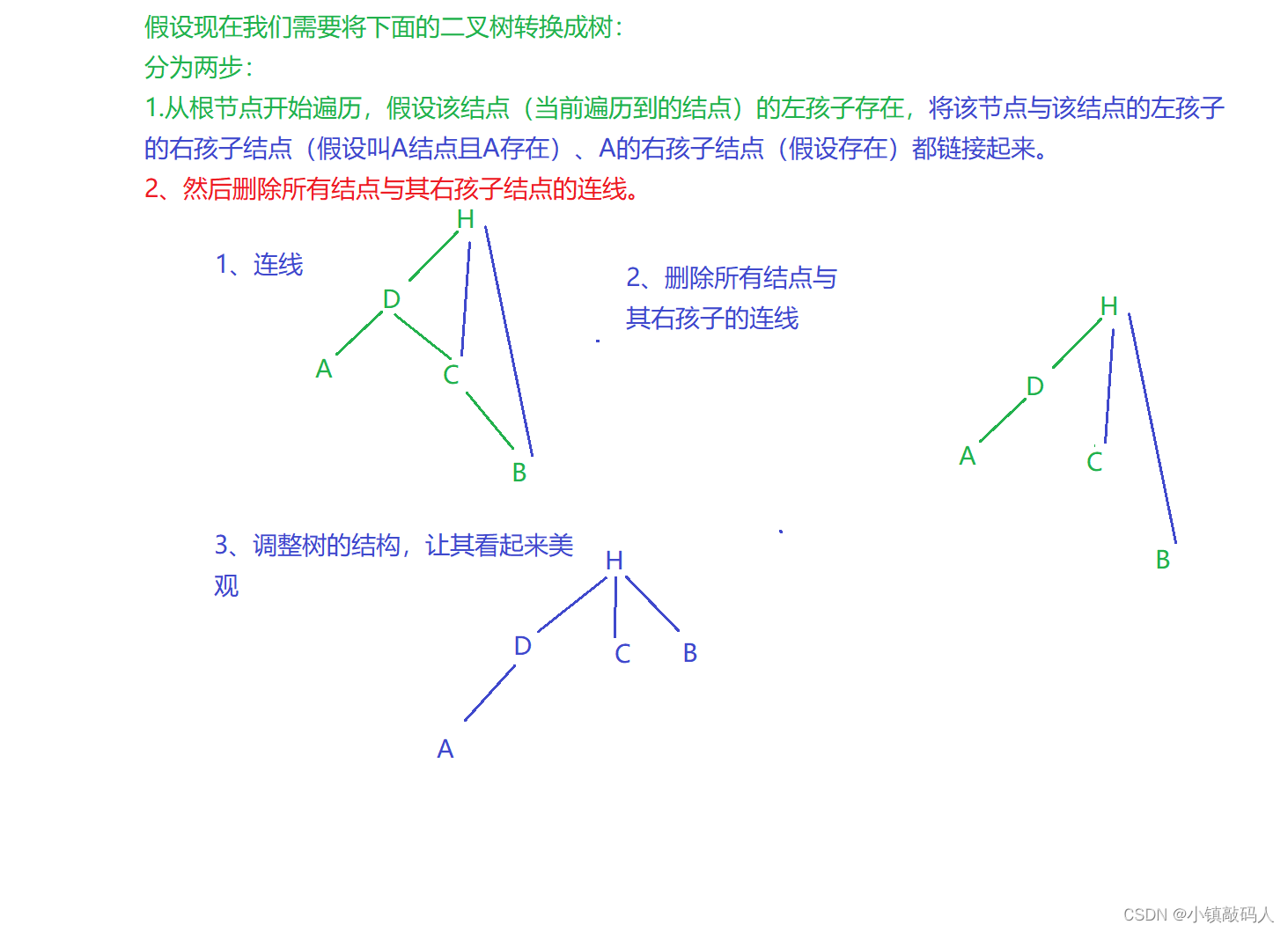
🐸 将二叉树如何转换成森林
很简单,一共有两步:
- 删除当前二叉树根节点与其右孩子结点的连线(使其独立成一个新的二叉树),然后看这个新的二叉树有没有右孩子结点,如果有继续删除连线。
- 将上述独立出来的所有二叉树都转化为树。
下面我们演示一下我们本题二叉树转化为森林的过程:
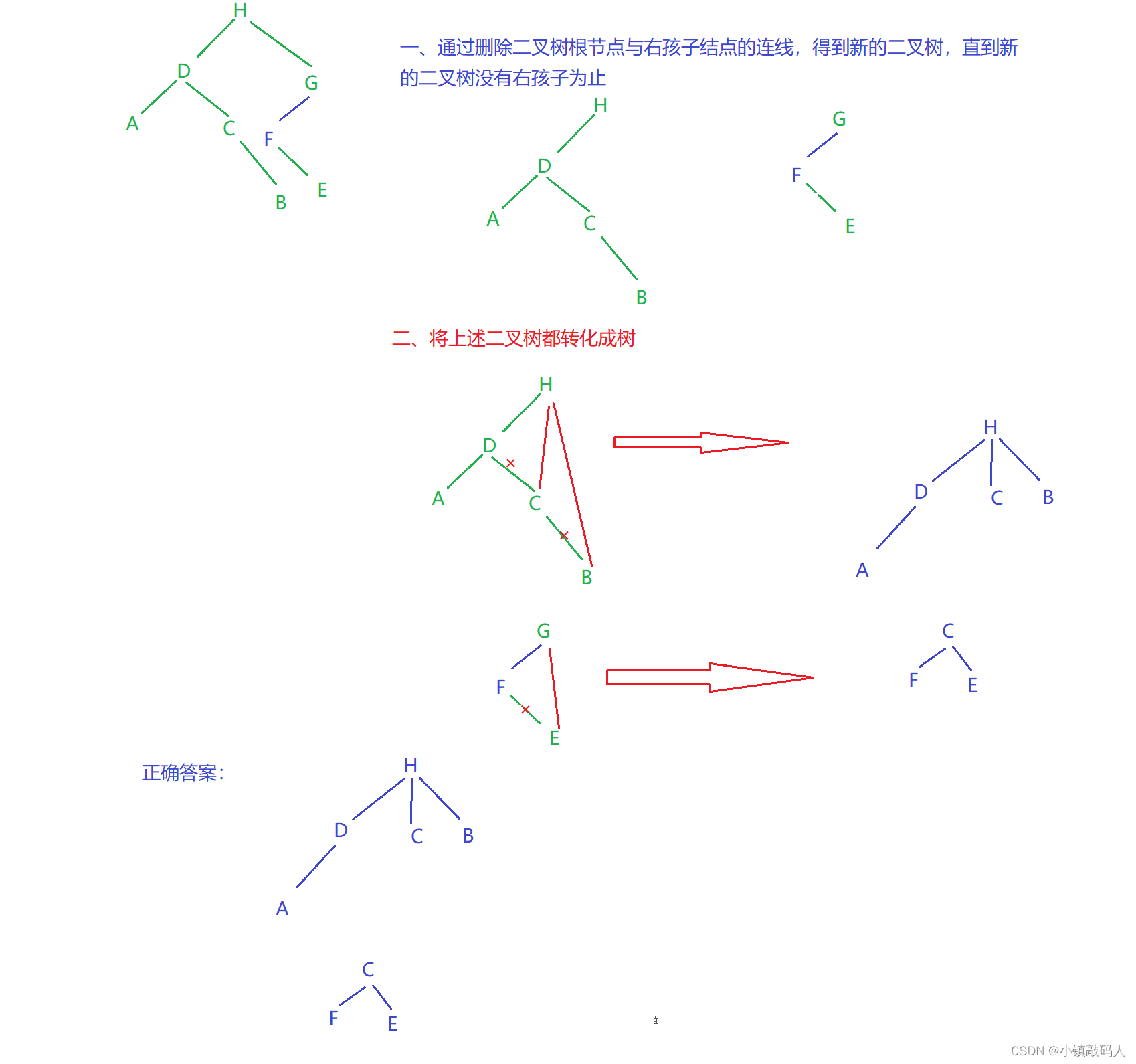
💑 标准答案(出自某搜题软件)
❄️ 大题2

💑 答案解析
本题看着没有什么头绪,只要让根结点存运算符,然后得到它的左子树和右子树求得的值(后序遍历),然后做运算,即可得到整个表达式的值。
代码:
typedef int DataType;typedef struct node
{DataType data;//存储数据char op;//存储运算符(可能有些结点只有运算符或者只有数据)struct node* left;struct node* right;
}*Pnode;float PostOrder(Pnode root)//假设对于是值的结点其运算符是一个特殊符号
{if (!root)//如果root为空return 0;float left_val, right_val = 0;//创建两个临时变量用来保存左边子树和右边子树的值float val = root->data;//返回值,如果当前结点没有左子树和右子树就证明其应该是一个值,而不是运算符left_val = PostOrder(root->left);//先去得到左边子树的值right_val = PostOrder(root->right);//再得到右边子树的值switch (root->op){case '+':val = left_val + right_val;break;case '-':val = left_val - right_val;break;case '*':val = left_val * right_val;break;case '/': val = left_val / right_val;break;default: break;//如果这个}return val;//返回结果
}
💑 标准答案

❄️ 大题3

💑 答案
此题和上面一道有重复,我们熟练之后可
以不用那么详细,照着先序遍历序列和中序遍历序列直接画出二叉树即可,就是要注意不要看错了。
💑 标准答案

❄️ 简答题1

💑 标准答案

❄️ 简答题2

答案:
链域就是指针域,每个结点有四个指针域。

💑 标准答案

❄️ 简答题3

💑 答案解析
💑 标准答案

标准答案的边界值对应下图两种情况:

😈 森林的先序遍历和中序遍历(可能出选择题)
考的不多,不需要作为重点,重点应该放在二叉树的遍历上。

😈 树转化为二叉树以及森林转化成二叉树
我们前面以及介绍过了将二叉树转化成树和将二叉树转化成森林,现在我们来介绍一下将树转化成二叉树以及将森林转化成二叉树:
- 将树转化成二叉树:
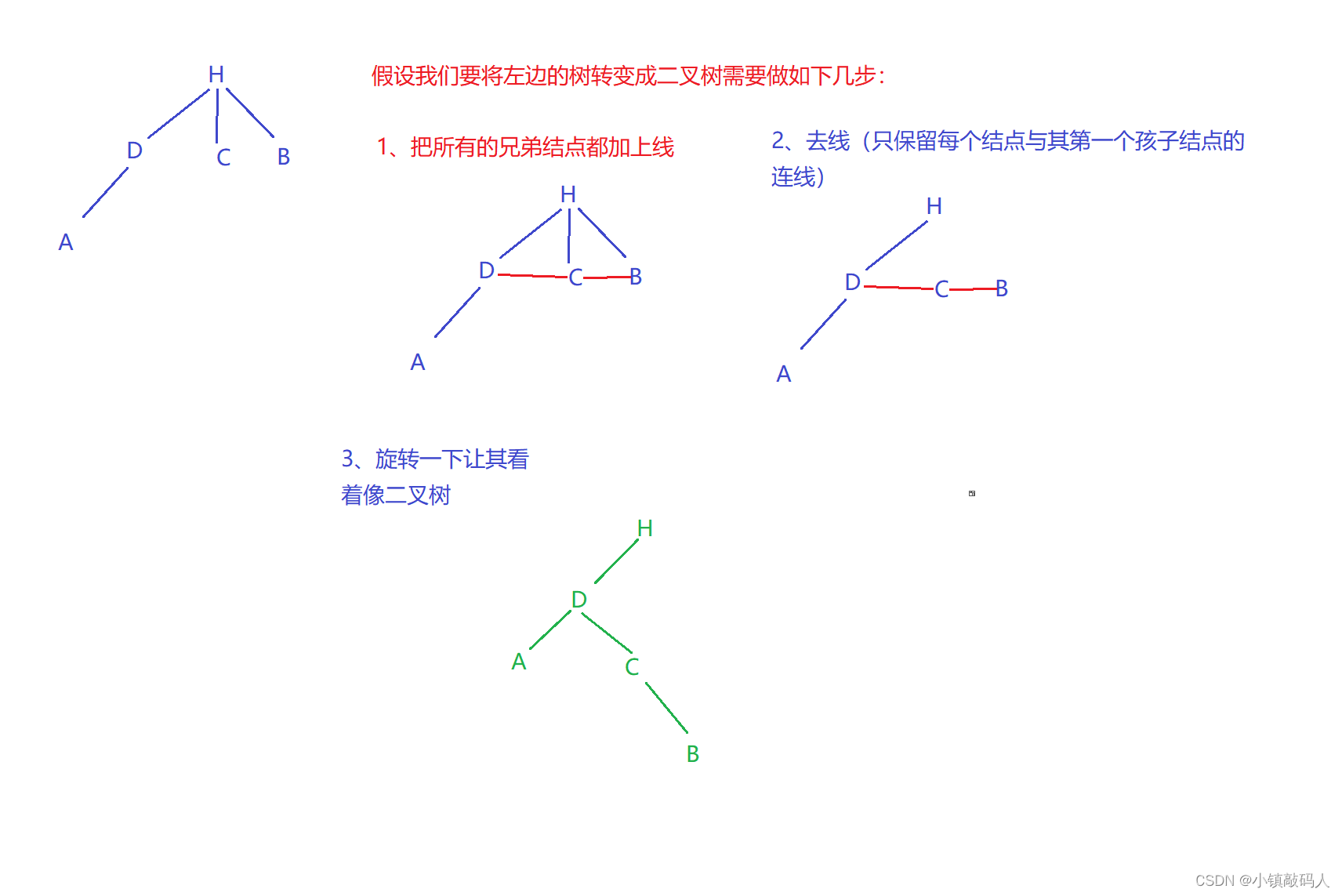
2. 将一棵森林转变成二叉树:

😈 哈夫曼树和哈弗曼编码(这里肯定会出大题)
知识点:

😈 大题1
这种题比较简单,基本上掌握一下基本套路就完事了。

❄️ 答案解析

😈 线索二叉树
线索二叉树就是将一个二叉树线索化的过程。
二叉树中有些左指针和右指针是空的,我们线索化的时候可以把它们利用起来。
- 无论是前序遍历,中序遍历还是后序遍历,如果一个节点没有左子树就让他的左指针指向他的前驱节点(前面一个要访问的结点),如果一个节点没有右子树,就让他的右指针指向他的后继节点(后面一个要访问的结点)。比较简单我们不再举例子。
💘 图
😈 图的连通性问题


😈 出度和入度
出度:某个顶点指向的顶点有几个,它的出度就是几。
入度:某个顶点被多少个顶点指向,它的入度就是几。
😈 带权无向图的最小生成树Prim、KrusKal算法
这两个算法都可以求最小生成树,我们只介绍Prim算法。
生成树:首先只有连通图才有生成树。生成树是所有顶点都连接在一起,但不存在回路的图。因为树就是不存在回路的。
最小生成树:所有生成树中使得各边权值总和最小的那棵生成树叫做最小生成树。
Prim算法的原理:从某一个顶点开始构建生成树,每次将代价最小(到原先的生成树权值
最小)的顶点加入这个生成树中构成新的生成树。(后面我们会用具体的题目来演示)
KrusKal算法的原理:Prime算法更倾向于点之间的关系,所以又叫做加点法。而KrusKal算法更倾向于边,它先将所有边按照权值的大小升序排列,然后依次按照边权值的大小开始建立最小生成树,如果加入当前权值最小的边时会导致出现回路,就舍弃,知道我们加入了n-1条边为止。
😈 有向无环图、拓扑排序
在图论中,如果一个有向图无法从某个顶点出发经过若干条边回到该点,则这个图是一个有向无环图(DAG图)。
拓扑排序的定义:
在有向无环图中,我们将全部活动(顶点和边的关系)排列成一个线性序列,使得这个图中中有弧<i,j>存在 则在这个序列中,i 一定排在j的前面 具有这种线性序列称为拓扑有序序列,相应的拓扑有序排序的算法称为拓扑排序。
拓扑排序的方法:

😈 大题1
下面题目涉及拓扑序列和最小生成树的构建比较重要,一定得掌握:

❄️ 答案解析

😈 大题2

(1)G1最多有n-1+n-2+n-3+…+1 = n ( n − 1 ) / 2 n(n-1)/2 n(n−1)/2。G1最少有n-1条边(不成环,但是连通)。

(2)和(3):

❄️ 标准答案

😈 关键路径和关键活动
关键路径这块的概念比较多。
AOE网:在一个表示工程的带权有向图中,顶点表示事件,用边来表示活动,边上的权值叫做活动持续的时间,这个有向图就是活动的网。
源点:在这个AOE网中,入度为0的点叫做源点。
终点:在这个AOE网,出度为0的点叫做终点。
AOE网的两个性质:
- 只有这个顶点的入度的活动都已经结束,这个顶点表示的事件才会开始。
- 只有这个顶点的事件开始后,从这个顶点出发的活动才会开始。
由于到达终点前,所有指向这个终点边上的活动都必须结束,所以完成整个工程的最短时间必须是那个源点到终点的最大长度,这个最大长度叫做关键路径。关键路径上的活动叫做关键活动。
事件的最早发生时间(ve(i)): 从源点出发(假设开始是0),该顶点的入度的各个活动中的最长时间(只有这个活动完成了,这个事件才能发生)。
事件的最晚发生时间(vl(i)):从终点出发,要在保证不耽误工期的情况下(关键路径,也就是最短顶点对应的事件完成的时间),在终点的最晚发生时间一定的条件下,倒推其它点的最晚发生时间。如果一个点有两个出度,推出了两个最晚发生时间,要取最小的那个(取更大的那个就有一个事件就不能完成了,工程最晚完成时间就要推迟)。
终点的事件最晚发生时间 = 最早发生时间。
活动的最早发生时间(ee(i)):某个活动开始的前提是那个顶点表示的时间开始了,所以这个值和这个活动所在边的起点的事件最早发生事件相等。
活动的最晚发生时间(el(i)):只有这个顶点的入度的活动都已经结束,这个顶点表示的事件才会开始,所以我们知道这个顶点的最晚发生时间,减去入度的活动的权值,就是对应的该活动的最晚发生时间。
el(i) = ee(i)的活动叫做关键活动,关键活动所连成的源点到终点路径叫做关键路径(可能有多条)。证明省略。
下面我们通过题来演示一下:
❄️ 大题2

💑 答案解析
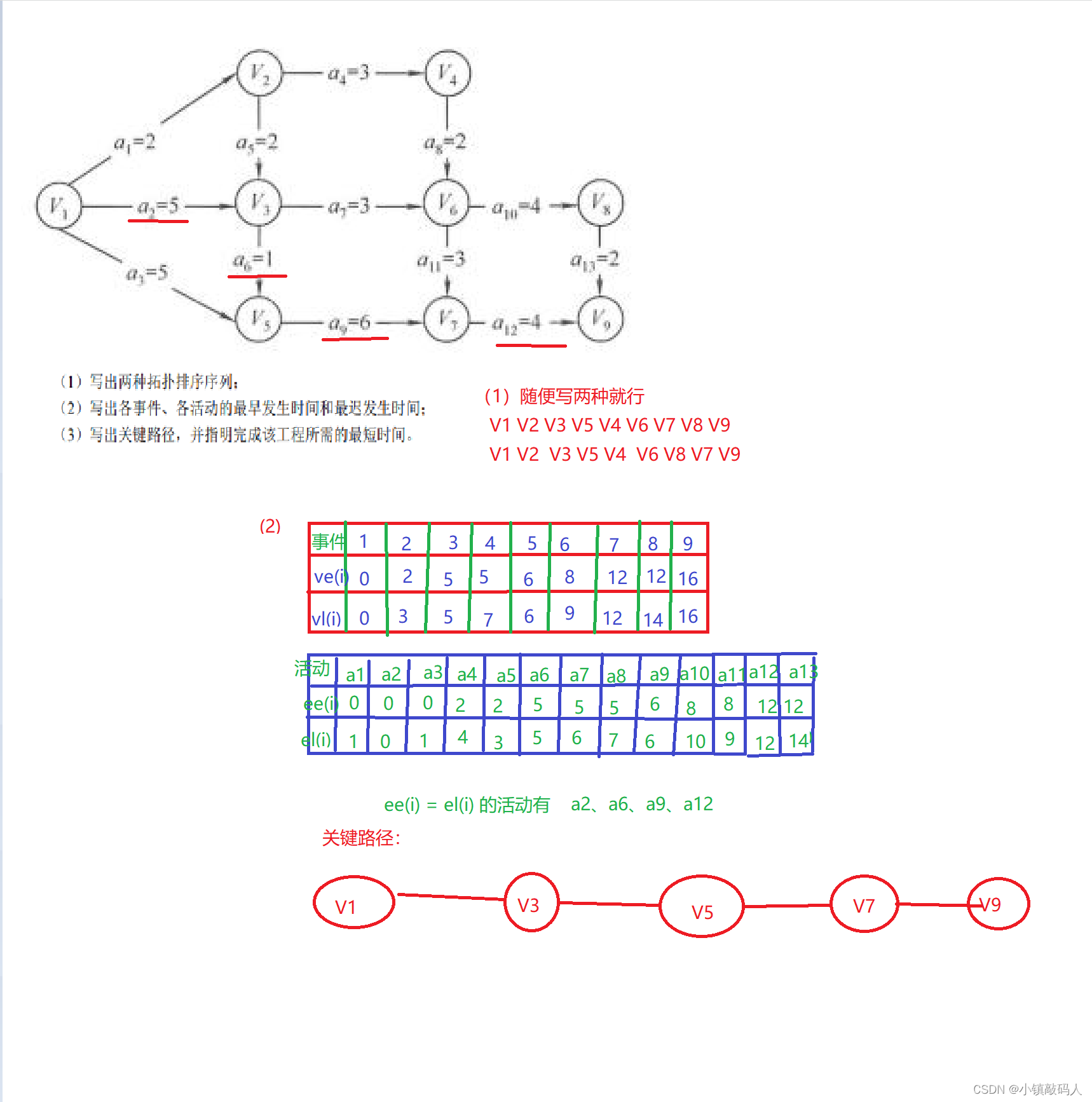
画两个表格,照着带权有向图直接写时间即可,只要了解了这四个概念所代表的意思,及其如何来求。
💑 标准答案


😈 图的遍历(广度优先和深度优先)
我们先介绍思想,大题三会有具体的题目来演示操作:
广度优先遍历(类似于树的广度优先遍历,也就是层序遍历):它的基本思想是这样的:
- 先任选一个顶点开始遍历。
- 依次遍历这个顶点的邻接顶点。
- 按照刚刚遍历的顺序去遍历邻接顶点的邻接点。
- 如果图中还有顶点没有访问完,任选一个没有被访问的顶点,按照上面的步骤,直到所有顶点被访问完。
深度优先遍历(类似于树的先序遍历,是其在图上的推广):它的基本思想如下:
- 先选一个顶点开始遍历。
- 再从这个刚刚访问的顶点
vi出发去访问它的第一个邻接点,重复本步骤,直到当前顶点没有邻接点。 - 返回刚刚访问过的且还有未被访问邻接点的顶点,找出并访问该顶点未被访问的邻接点,执行步骤2。
- 重复执行以上步骤,直到所有顶点被访问完。
😈 最短路径
最短路径有四种算法可以求,详细原理可以看博主这篇博客。
❄️ 大题3
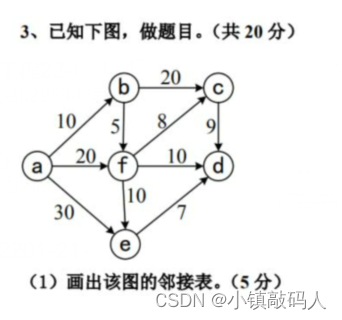

💑 答案解析

💑 标准答案

答案的深度优先遍历序列是错误的。
💘 查找
😈 静态查找表:顺序查找、折半查找
顺序查找:按照顺序在表(一般是数组)中依次查找,时间复杂度是 O ( N ) O(N) O(N)。一般不用。
折半查找:即我们所说的二分查找算法。这个算法的前提是表已经有序。时间复杂度是 O ( l o g N ) O(logN) O(logN)。
❄️ 大题1


💑 答案解析

💑 标准答案

.
😈 动态查找表: 二叉排序树、二叉平衡树、m阶B树
❄️ 二叉排序树
请看博主这篇博客
这个很简单考的不多,重点看二叉平衡树和m阶B树。
❄️ 二叉平衡树
二叉树平衡树上课只介绍了AVL树。
AVL树是平衡搜索二叉树的一种,它是为了解决普通二叉搜索树不平衡的问题,它通过保持每个结点的左右两棵子树的高度差不超过1来维持查找效率。
AVL树有以下性质,满足以下性质的二叉树也叫做高度平衡:
- 左右子树的高度差不超过1(-1,0,1)。
- 左右子树也为
AVL树
- 我们这里的左右子树的高度均为左右子树的最长路径的结点个数。
如果一棵二叉树是高度平衡的,那么它就是平衡二叉树,它的高度是 O ( l o g N ) O(logN) O(logN),搜索的效率也在 O ( l o g N ) O(logN) O(logN)量级。
我们重点来看一下AVL树的插入调整:
-
左单旋
在当前高度较高的某节点的右子树的右边插入了一个新结点引发了不平衡,需要右单旋。 -
右单旋
在当前高度较高的某节点的左子树的左边插入了一个新结点引发的不平衡,需要左单旋。 -
左右双旋
当前高度较高的某节点的左子树的右子树插入了一个结点,引发了不平衡,需要先左单旋,再右单旋转。 -
右左双旋
当前高度较高的某节点的右子树的左子树插入了一个结点,引发了不平衡,需要先右单旋,再左单旋转。
我们用具体的题目来演示如何旋转:
❄️ 大题1

💑 答案解析

💑 标准答案

这个答案有点问题,最后一个数据65插入的它没写,命名的话博主是按照旋转的方向命名,这个答案是按照插入的方向命名。
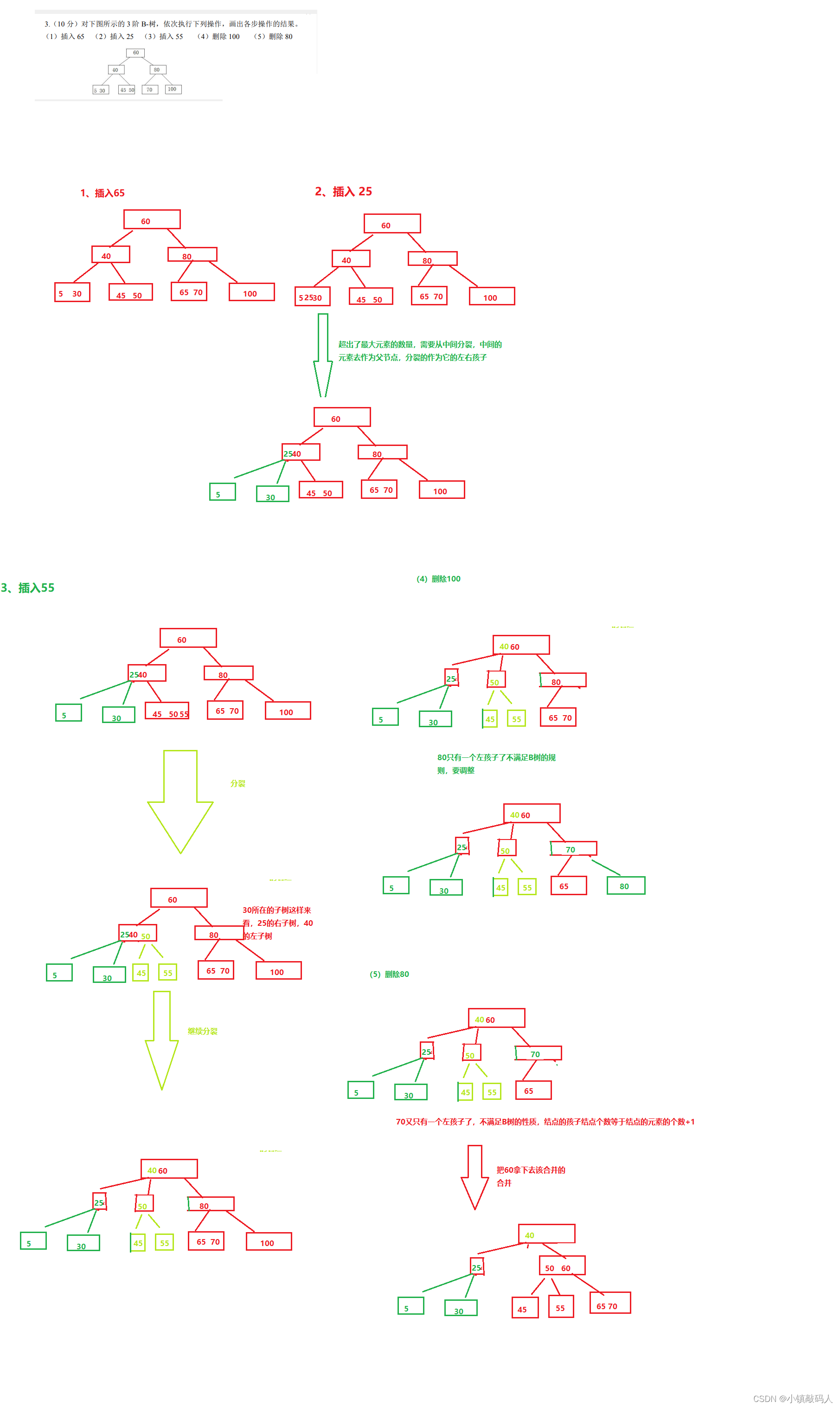
😈 B树
B树是多路平衡二叉树。
- B树的性质

2. B树的插入和删除
我们用下面的题目来演示,如果你没有搞懂,请自行去B站上学习。
❄️ 大题2

💑 答案解析
😈 哈希表
❄️ 哈希表的长度、哈希表的装填因子等
哈希表的长度是指的是哈希表可以存储的最大元素数量。
哈希表的装填因子是指的是当前已经存储的元素的数量(桶的数量)/ 哈希表的长度
❄️ 常用的构造哈希函数的方法
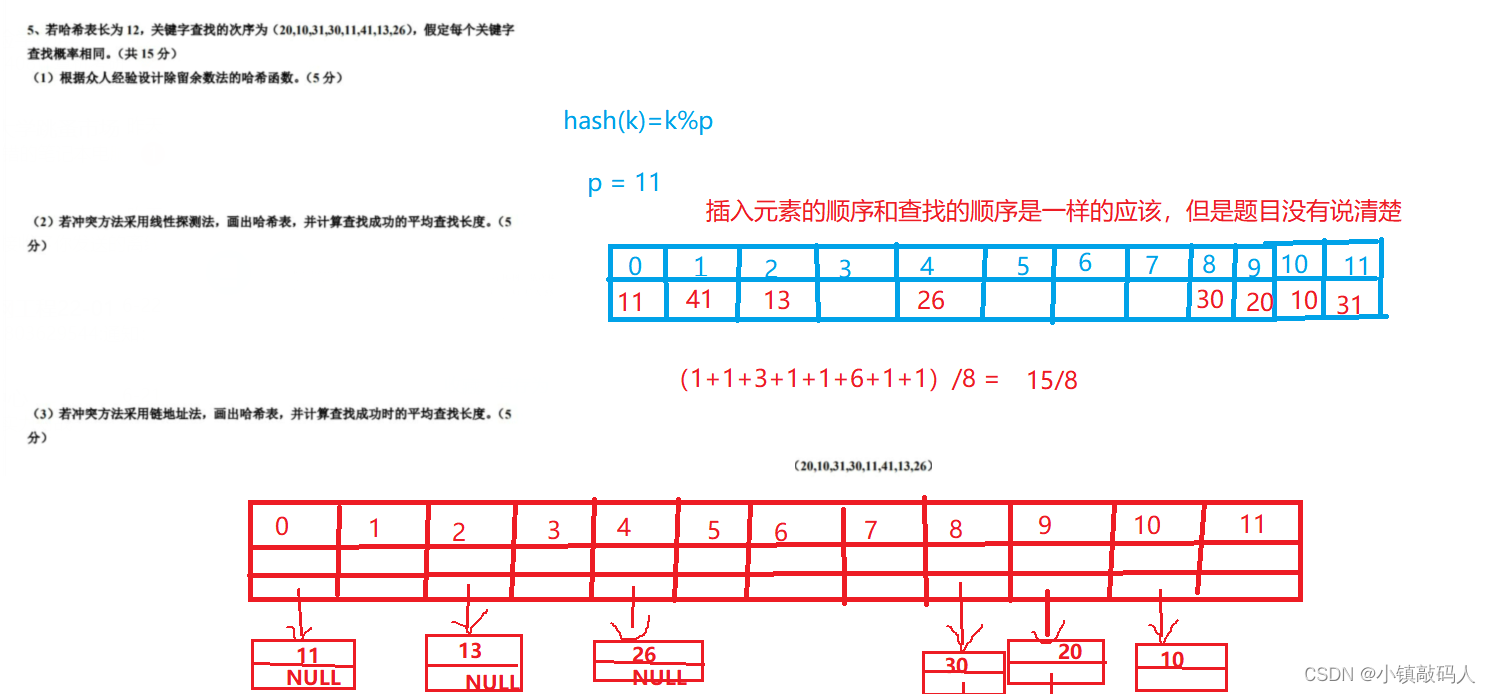
- 除留余数法
除留取余法是将关键字除以一个不大于哈希表长度的正整数p(一般是小于哈希表长度的最大质数),并将所得余数作为地址。
具体而言,除留取余法的步骤如下:
1、选择一个不大于哈希表长度的正整数p(一般是小于哈希表长度的最大质数)作为模。
2、将关键字对p取模作为哈希表的索引地址。
- 直接定址法
直接定址法就是将关键字作为索引地址,关键字就是下标,要求关键字范围小且连续,否则会造成空间浪费。
❄️ 处理冲突的方法
- 开放寻址法
原理是当发生冲突时,是以当前地址为基准,去通过寻址找到下一个地址。
常用的寻址方法:- 线性探测:发生冲突时,从当前地址开始往后面去找空地址,如果到达表尾,就回到表头继续找,直到找到或者已经遍历全表。
- 二次探测(平方探测):发生冲突时,从当前地址开始,左右跳跃,di = 1 2 , − 1 2 , 2 2 , − 2 2 , 3 2 , − 3 2 . . . . . . 1^2,-1^2,2^2,-2^2,3^2,-3^2...... 12,−12,22,−22,32,−32......直到找到为止。
2.链地址法
又叫做拉链法,这个方法是把哈希表的每个位置看成一个桶,每个桶里面都是一个链表,然后如果发生冲突了,就把新的结点,尾插到这个位置桶的尾部。
我们通过下面的题目来演示:
❄️ 大题3

💑 答案解析
相关文章:

【征服数据结构】:期末通关秘籍
【征服数据结构】:期末通关秘籍 💘 数据结构的基本概念😈 数据结构的基本概念😈 逻辑结构和存储结构的区别和联系😈 算法及其特性😈 简答题 💘 线性表(链表、单链表)&…...

GIT 基于master分支创建hotfix分支的操作
基于master分支创建hotfix分支的操作通常遵循以下步骤: 切换到master分支: 首先,确保你的工作区是最新的,并且你在master分支上。如果不在master分支,你需要先切换过去。 Bash git checkout master 拉取最新的master…...
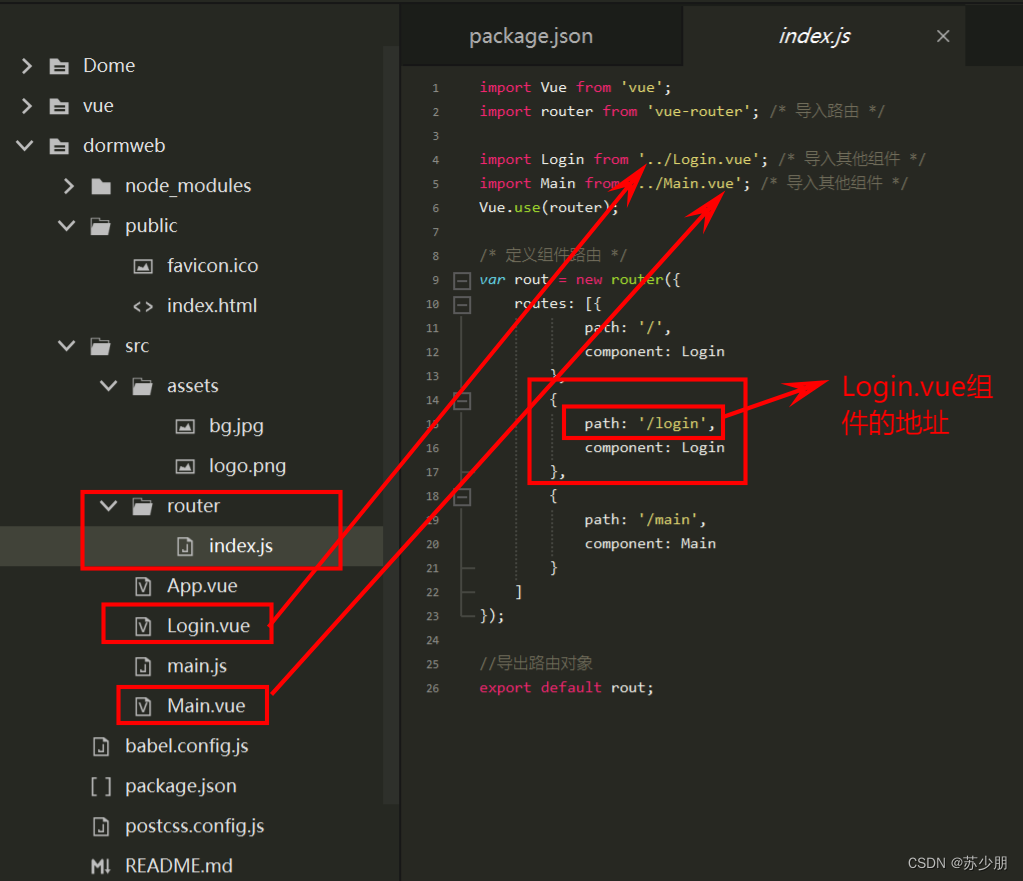
Vue-CLI脚手架与node.js安装
前言: Vue-CLI 是一个基于 Vue.js 快速开发单页应用的官方脚手架工具,能够帮助开发者快速搭建前端项目的基础结构。在开始使用 Vue-CLI 前,首先需要安装 Node.js,因为 Vue-CLI 是基于 Node.js 构建的。 Node.js 是一个基于 Chrom…...
自适应站长跑路单页网站源码
跑路单页HTML源码自行修改文字就行了,上传到服务器里面运行即可,本地运行的话音乐会加载不出来,涉及到跨域问题 自适应站长跑路单页网站源码...

Java基础(判断和循环)
一、流程控制语句-顺序结构 顺序结构语句是Java程序默认的执行流程,按照代码的先后顺序,从上到下依次执行。 二、流程控制语句-分支结构(分支结构包括if、switch) if语句:在程序中用来进行判断 1、If语句的第一种格式…...

51单片机第12步_使用stdio.h库函数仿真串口通讯
本章介绍如何使用stdio.h库函数仿真串口通讯,学会使用view下面的“serial window #1”,实现模拟串口通讯。 Keil C51中有一些关键字,需要牢记: interrupt0:指定当前函数为外部中断0; interrupt1:指定当前函数为定时器0中断&…...

simulink-esp32开发foc电机
1. ESP32 和 STM32 都是流行的微控制器,但它们的刷写方式有所不同。 ESP32 ESP32 可以通过以下几种方式刷写: USB 下载模式:这是最常见的一种刷写方式。将 ESP32 连接到计算机的 USB 端口,然后将 ESP32 置于下载模式。可以使用…...

Python教程--基本技能
】TOC 5.1 解析命令行参数 在Python中,解析命令行参数是一项常见的任务,尤其是在开发命令行工具或脚本时。Python标准库提供了argparse模块,它可以帮助你轻松地编写用户友好的命令行接口。下面是使用argparse模块解析命令行参数的基本步骤&…...
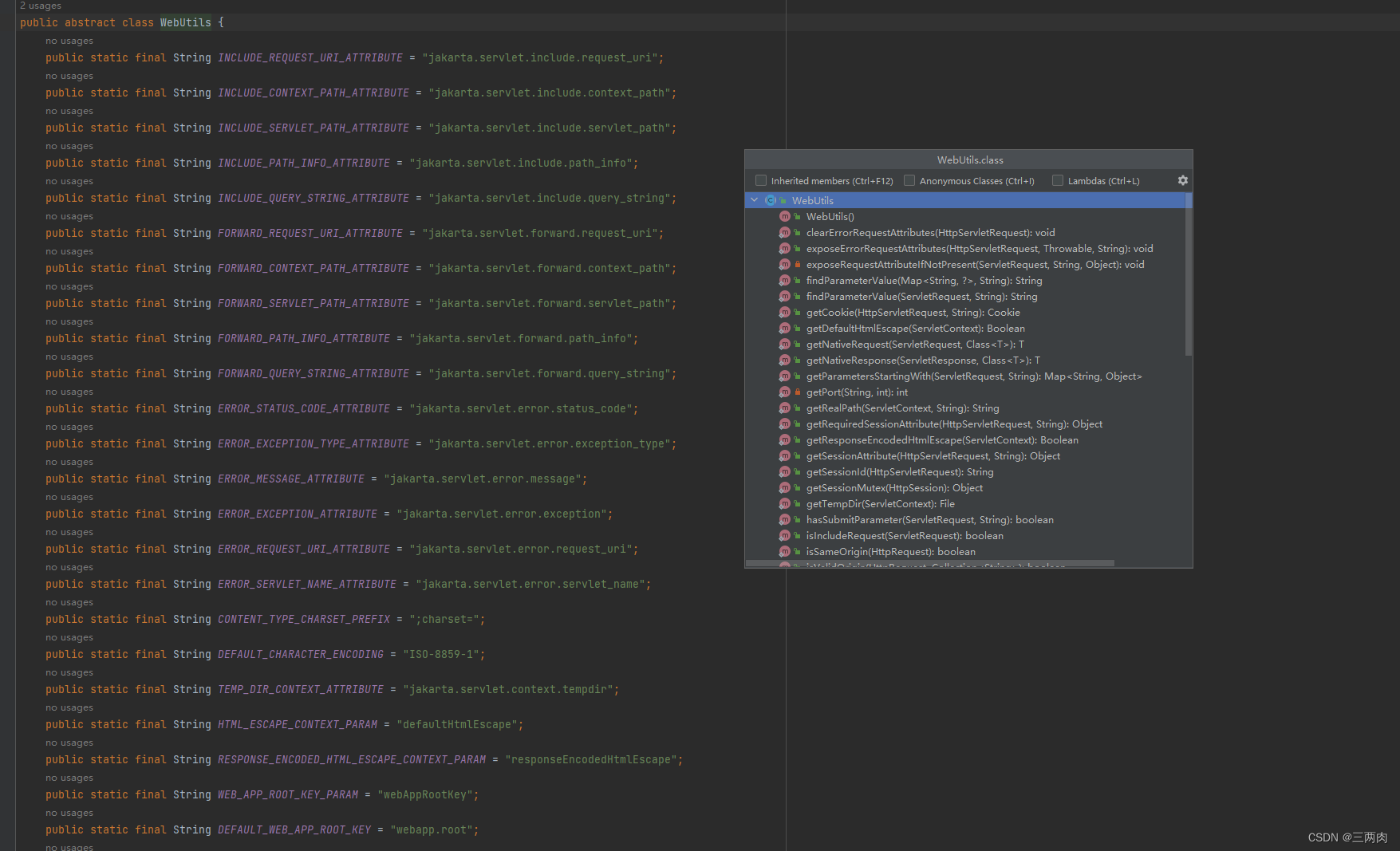
干货分享:Spring中经常使用的工具类(提示开发效率)
环境:Spring5.3…30 1、资源工具类 ResourceUtils将资源位置解析为文件系统中的文件的实用方法。 读取classpath下文件 File file ResourceUtils.getFile(ResourceUtils.CLASSPATH_URL_PREFIX "logback.xml") ; // ...读取文件系统文件 file Resou…...
一文讲懂npm link
前言 在本地开发npm模块的时候,我们可以使用npm link命令,将npm 模块链接到对应的运行项目中去,方便地对模块进行调试和测试 用法 包链接是一个两步过程: 1.为依赖项创建全局软链npm link。一个符号链接,简称软链&a…...
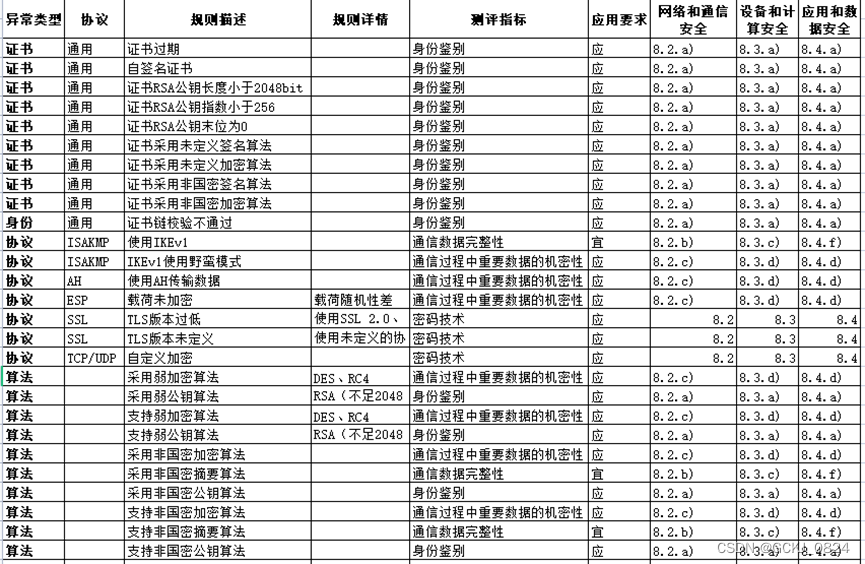
观成科技:证券行业加密业务安全风险监测与防御技术研究
摘要:解决证券⾏业加密流量威胁问题、加密流量中的应⽤⻛险问题,对若⼲证券⾏业的实际流量内容进⾏调研分析, 分析了证券⾏业加密流量⾯临的合规性⻛险和加密协议及证书本⾝存在的⻛险、以及可能存在的外部加密流量威 胁,并提出防…...

使用Swoole开发高性能的Web爬虫
使用swoole开发高性能的web爬虫 Web爬虫是一种自动化获取网络数据的工具,它可以在互联网上收集数据,并且可以被应用于各种不同的领域,如搜索引擎、数据分析、竞争对手分析等。随着互联网规模和数据量的快速增长,如何开发一个高性…...

【Elasticsearch】Elasticsearch索引创建与管理详解
文章目录 📑引言一、Elasticsearch 索引的基础概念二、创建索引2.1 使用默认设置创建索引2.2 自定义设置创建索引2.3 创建索引并设置映射 三、索引模板3.1 创建索引模板3.2 使用索引模板创建索引 四、管理索引4.1 查看索引4.2 更新索引设置4.3 删除索引 五、索引别名…...

[数据集][目标检测]棉花检测数据集VOC+YOLO格式389张1类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):389 标注数量(xml文件个数):389 标注数量(txt文件个数):389 标注类别…...

使用Java实现实时数据处理系统
使用Java实现实时数据处理系统 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 引言 在当今信息爆炸的时代,实时数据处理系统变得越来越重要。无论…...

整合web-socket的常见bug
整合文章连接 此文是记录我上网查找整合方案时候踩的坑,特别是注册失败的问题,比如还有什么去掉Compoent就可以,但是这样这个端点就失效了 特别是报错: at org.springframework.web.socket.server.standard.ServerEndpointExporter.registerEndpoint(ServerEndpointExporter.…...

Python 中字符串的常用操作都有哪些?
在 Python 中字符串的表达方式有四种 一对单引号 一对双引号 一对三个单引号 一对三个双引号 a ‘abc’ b “abc” c ‘’‘abc’’’ d “”“abc”"" print(type(a)) # <class ‘str’> print(type(b)) # <class ‘str’> print(type©) # <…...

FFmpeg 硬件编码加速文档介绍
介绍 硬件访问:许多平台提供了对专用硬件的访问,这些硬件可以用于执行解码、编码或过滤等视频相关操作。 性能与资源使用:使用硬件可以加快某些操作的速度或减少其他资源(特别是CPU)的使用,但可能会产生不同的结果或质量较低,或带来在使用纯软件时不存在的额外限制。 硬…...

【Matlab函数分析】imread从图形文件读取图像
🔗 运行环境:Matlab 🚩 撰写作者:左手の明天 🥇 精选专栏:《python》 🔥 推荐专栏:《算法研究》 #### 防伪水印——左手の明天 #### 💗 大家好🤗ᾑ…...

零基础光速入门AI绘画,SD保姆攻略
前言 大家好,我是AI绘画咪酱。一名AIGC狂热爱好者,目前正在AI绘画领域进行深入的探索。 我花了一个月时间把SD研究了一遍,秉持着用有趣、易懂的文字让小白也可以零基础光速使用SD(stable diffusion)入门AI绘画&#…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
