ubuntu安装QT
以QT5.15.14为例
下载地址:Index of /archive/qt
安装步骤:
- 解压qt-everywhere-src-5.15.14
- 运行:
cd qt-everywhere-src-5.15.14 mkdir build cd build ../configure -prefix /opt/qt5.15.14 -opensource -confirm-license make -j16 sudo make install
问题解答:
1. 若出现如下错误:
ERROR: The OpenGL functionality tests failed!
You might need to modify the include and library search paths by editing QMAKE_INCDIR_OPENGL[_ES2],
QMAKE_LIBDIR_OPENGL[_ES2] and QMAKE_LIBS_OPENGL[_ES2] in the mkspec for your platform.解决方式:
sudo apt-get install libgl1-mesa-devsudo apt-get install libglu1-mesa-dev freeglut3-dev mesa-common-dev
2. 若出现如下问题 :
/usr/include/c++/11/type_traits:38:10: fatal error: bits/c++config.h: No such file or directory解决方式:安装gcc-9版本,由于系统内存在多个版本gcc,可以使用update-manager进行管理
sudo apt install update-manager
sudo apt install gcc-9 g++-9 gcc-9-multilib g++-9-multilib
sudo update-alternatives --install /usr/bin/gcc gcc /usr/bin/gcc-9 1
sudo update-alternatives --install /usr/bin/g++ g++ /usr/bin/g++-9 13. 若出现一下错误:
./configure -prefix $PWD/qtbase -opensource -nomake tests bash: ./configure:/bin/sh^M:解释器错误: 没有那个文件或目录 解决方案:
#你可以使用dos2unix工具将文件的换行符从Windows风格转换为Unix/Linux风格sudo apt-get install dos2unix
find . -type f -exec dos2unix {} \;
相关文章:

ubuntu安装QT
以QT5.15.14为例 下载地址:Index of /archive/qt 安装步骤: 解压qt-everywhere-src-5.15.14运行: cd qt-everywhere-src-5.15.14 mkdir build cd build ../configure -prefix /opt/qt5.15.14 -opensource -confirm-license make -j16 sudo…...
DataGrip 2024 po for Mac 数据库管理工具解
Mac分享吧 文章目录 效果一、下载软件二、开始安装1、双击运行软件(适合自己的M芯片版或Intel芯片版),将其从左侧拖入右侧文件夹中,等待安装完毕2、应用程序显示软件图标,表示安装成功3、打开访达,点击【文…...

《C++ Primer》导学系列:第 13 章 - 拷贝控制
13.1 拷贝、赋值与析构函数 拷贝控制是C++中类设计的重要组成部分,用于管理对象的复制、赋值和销毁过程。理解并正确实现拷贝控制函数(拷贝构造函数、拷贝赋值运算符和析构函数)对于编写健壮和高效的C++程序至关重要。 13.1.1 拷贝构造函数 拷贝构造函数用于创建对象的副…...

c++ 图论2 深度优先算法和广度优先算法
修改一下深度优先算法和广度优先算法,标出每一个节点相对于遍历起始位置的层级,遍历起始起点为第一层,和第一层相连的节点为第二层,以此类推 定义一个新的结构 struct NodeWithLevel {TreeNode* node;int level;NodeWithLevel(T…...
【Qt】初识QtQt Creator
一.简述Qt 1.什么是Qt Qt 是⼀个 跨平台的 C 图形⽤⼾界⾯应⽤程序框架 。它为应⽤程序开发者提供了建⽴艺术级图形界⾯所需的所有功能。它是完全⾯向对象的,很容易扩展。Qt 为开发者提供了⼀种基于组件的开发模式,开发者可以通过简单的拖拽和组合来实现…...
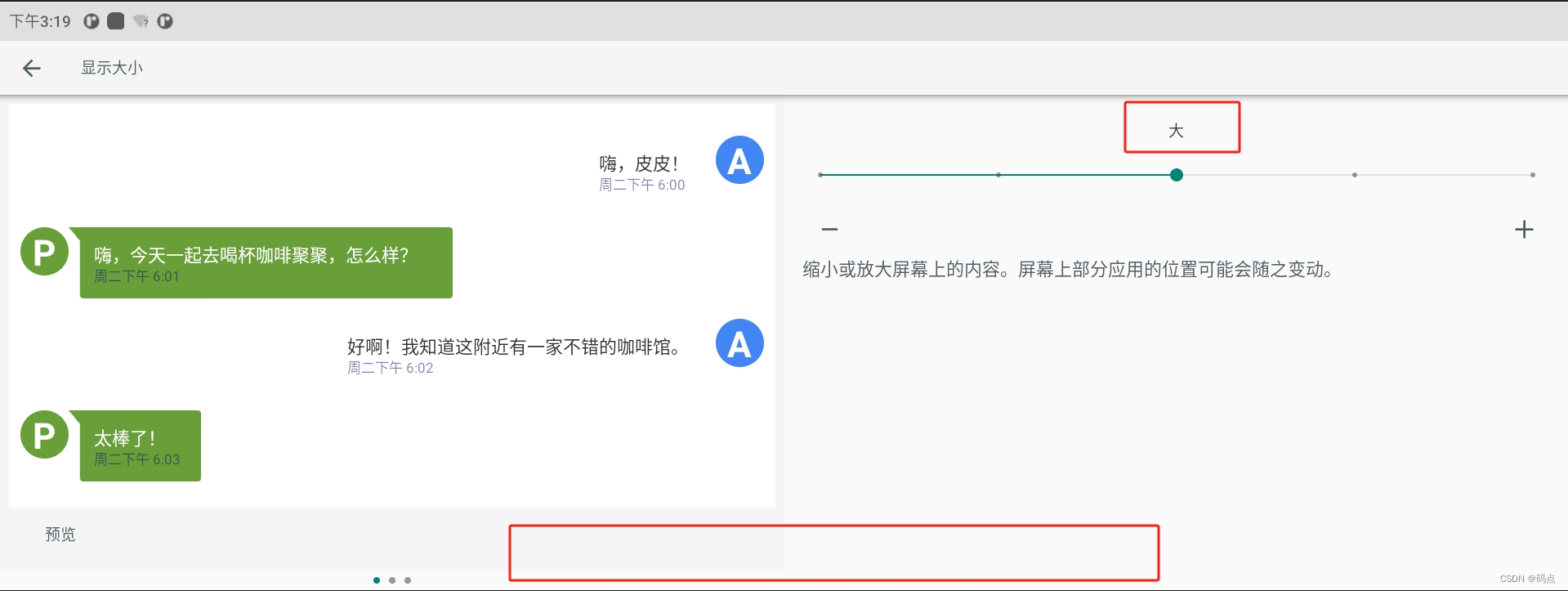
Android 11.0 修改系统显示大小导航栏消失
Android 11.0 修改系统显示大小导航栏消失 1.显示大小设置为大时,导航栏图标不显示。 设置为大,较大,最大时,导航栏图标不显示。 2.开始怀疑是导航栏被隐藏了,各种折腾无效。 3.发现: frameworks/base/pa…...

RocketMQ源码学习笔记:Producer启动流程
这是本人学习的总结,主要学习资料如下 马士兵教育rocketMq官方文档 目录 1、Overview1.1、创建MQClientInstance1.1.1、检查1.1.1、MQClientInstance的ID 1.2、MQClientInstance.start() 1、Overview 这是发送信息的代码样例, DefaultMQProducer produ…...

Node.js 和浏览器环境中都使用 WebSocket
使用WebSocket为什么不适配双端 浏览器环境本身就支持 WebSocket,直接使用 JavaScript 内置的 WebSocket 对象来建立连接。 Node中本身并没有内置 WebSocket 协议的支持,所以需要使用第三方库 ws来实现 WebSocket 功能。 一. 使用跨平台 WebSocket 库 …...

css美化滚动条样式
效果展示 实现 滚动条宽,高度 /* 整体滚动条 */ ::-webkit-scrollbar {width: 10px; }/* 滚动条轨道 */ ::-webkit-scrollbar-track {background-color: #ffffff;border-radius: 6px; }/* 滚动条滑块 */ ::-webkit-scrollbar-thumb {background-color: #888;borde…...
)
由浅入深,走进深度学习(补充篇:转置卷积和FCN)
本期内容是针对神经网络层结构的一个补充,主要内容是:转置卷积和全连接卷积网络 相关内容: 由浅入深,走进深度学习(2)_卷积层-CSDN博客 由浅入深,走进深度学习(补充篇:…...

Linux基础篇——目录结构
基本介绍 Linux的文件系统是采用级层式的树状目录结构,在此结构中的最上层是根目录"/",然后在根目录下再创建其他的目录 在Linux中,有一句经典的话:在Linux世界里,一切皆文件 Linux中根目录下的目录 具体的…...

星际编码:Swifter.Json,.NET宇宙中的数据处理新星
概述 在数字化的星辰大海中,数据是宇宙的通用语言。在.NET这一广袤的星系中,JSON作为信息交换的媒介,扮演着至关重要的角色。今天,我们要探索的是一颗新星——Swifter.Json,一个功能全面且性能卓越的JSON序列化和反序列…...

python 压缩数据
requests 是 Python 中一个非常流行的 HTTP 库,用于发送各种 HTTP 请求。下面是一个使用 requests 库发送简单 GET 请求和 POST 请求的示例: 首先,确保你已经安装了 requests 库。如果还没有安装,可以使用 pip 进行安装ÿ…...

nacos在k8s上的集群安装实践
目录 概述实践nfs安装使用 k8s持久化nacos安装创建角色部署数据库执行数据库初始化语句部署nacos ingress效果展示问题修复 结束 概述 本文主要对 nacos 在k8s上的集群安装 进行说明与实践。主要版本信息,k8s: 1.27.x,nacos: 2.0.3。运行环境为 centos 7…...

数据结构—判断题
1.数据的逻辑结构说明数据元素之间的顺序关系,它依赖于计算机的存储结构。 答案:错误 2.(neuDS)在顺序表中逻辑上相邻的元素,其对应的物理位置也是相邻的。 答案:正确 3.若一个栈的输入序列为{1, 2, 3, 4, 5},则不…...

树莓派挂载的移动硬盘badblocks坏道屏蔽,以这个为准
!!!use 这里要设置块大小和磁盘相同 badblocks -b 4096 -s -c 512 -v -o /a/2/bads4.txt /dev/sda5 检测完重新检测跳过之前的记录 badblocks -i /a/2/bads4.txt -b 4096 -s -c 512 -v -o /a/2/bads5.txt /dev/sda5 可以查看磁盘具体block总数和大小 sudo dumpe2fs /dev/sda5 …...
Unity开箱即用的UGUI面板的拖拽移动功能
文章目录 👉一、背景👉二、效果图👉三、原理👉四、核心代码👉五,总结 👉一、背景 之前做PC项目时常常有面板拖拽移动的需求,今天总结封装一下,做成一个随时随地可复用的…...
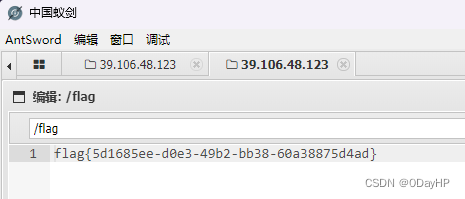
春秋云境:CVE-2022-25411[漏洞复现]
根据题目提示和CNNVD优先寻找后台管理地址 靶机启动后,使用AWVS进行扫描查看网站结构 在这里可以看到后台管理的登录地址:/admin/,根据题目提示可知是弱口令 尝试admin、123456、admin666、admin123、admin888...等等常见弱口令 正确的账户…...
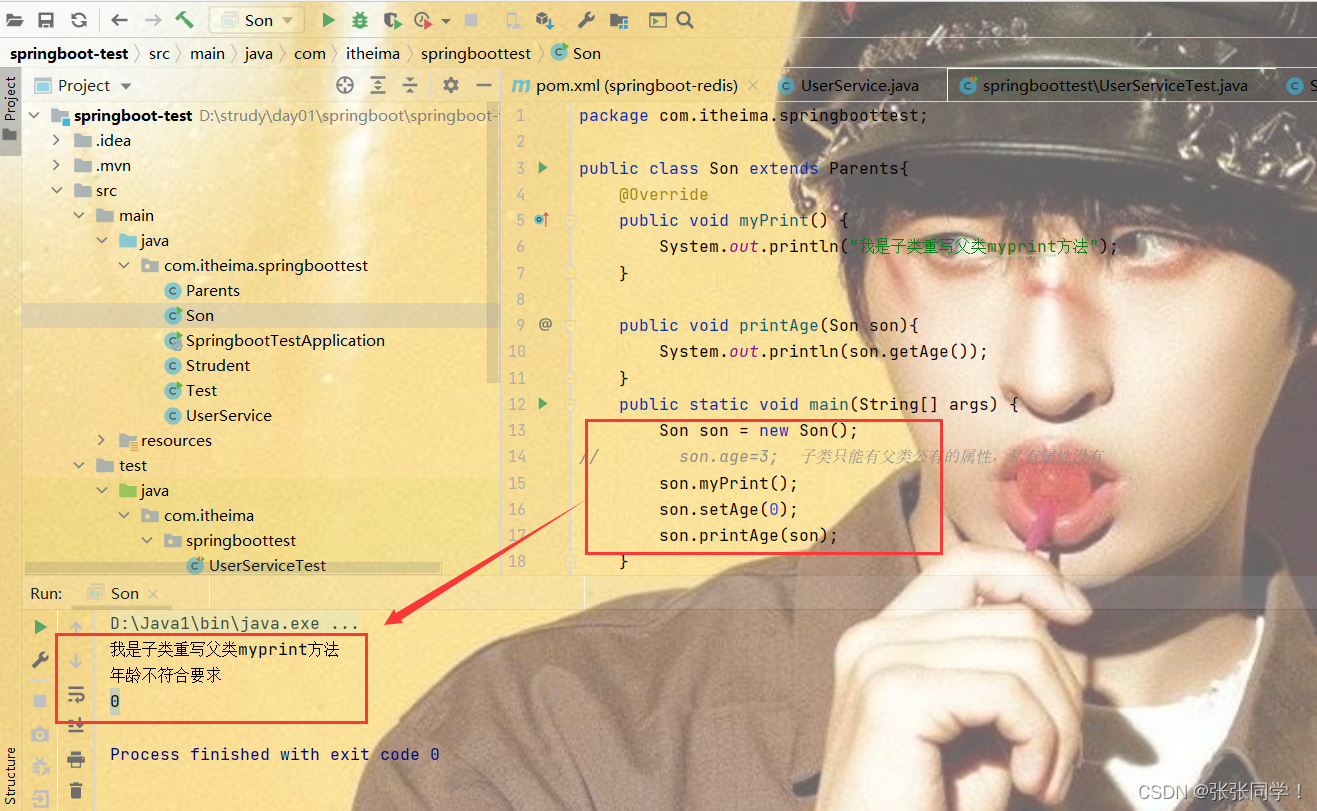
java基础知识点全集
JAVA的所有知识点 一、基础的数组、数据类型、输入输出二、类与对象1. 三大特征(1) 封装(2)继承(3)多态 2. 类的实例化(1) 类通过NEW来创建(2) 类的继承&…...
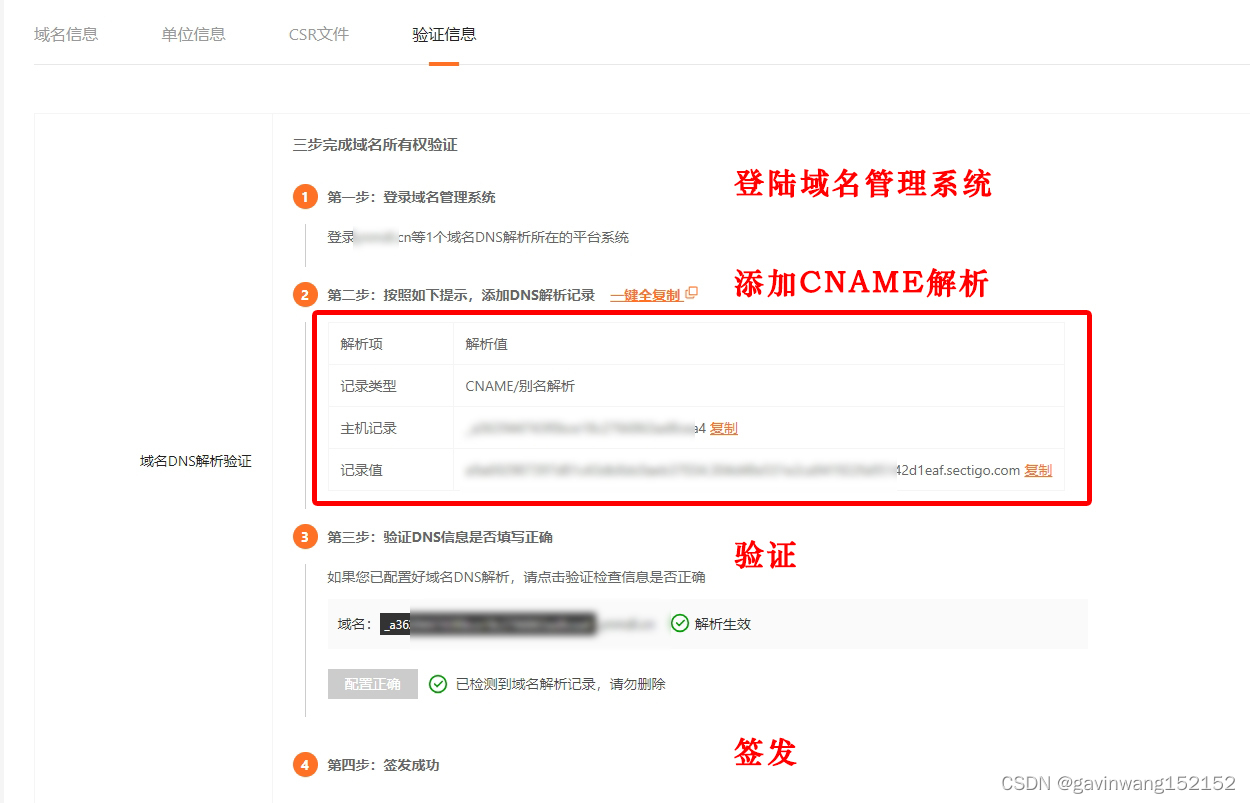
如何完成域名解析验证
一:什么是DNS解析: DNS解析是互联网上将人类可读的域名(如www.example.com)转换为计算机可识别的IP地址(如192.0.2.1)的过程,大致遵循以下步骤: 查询本地缓存:当用户尝…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
