深度学习之激活函数
激活函数的公式根据不同的函数类型而有所不同。以下是一些常见的激活函数及其数学公式:
- Sigmoid函数:
- 公式:f(x)=

- 特性:输出范围在0到1之间,常用于二分类问题,将输出转换为概率值。但存在梯度消失问题,尤其在输入值较大或较小时。
- 公式:f(x)=
- Tanh函数(双曲正切函数):
- 公式:f(x)=
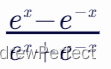
- 特性:输出范围在-1到1之间,具有更广的取值范围,且均值为0,可以中心化输入信号。但也存在梯度消失问题。
- 公式:f(x)=
- ReLU(Rectified Linear Unit)函数:
- 公式:f(x)=max(0,x)
- 特性:当x<0时,输出为0;当x>0时,输出为x。ReLU函数计算简单,速度快,且解决了梯度消失问题(在x>0的区域)。但存在“死区”问题,即当x<0时,梯度为0。
- Leaky ReLU函数:
- 公式:f(x)=max(αx,x)(其中α是一个很小的正数,如0.1)
- 特性:Leaky ReLU函数试图解决ReLU的“死区”问题,当x<0时,输出为αx而不是0。
- Softmax函数:
- 公式:softmax(xi)=
 (其中xi是输入向量中的第i个元素,N是输入向量的维度)
(其中xi是输入向量中的第i个元素,N是输入向量的维度) - 特性:Softmax函数是多分类任务中常用的激活函数,它将每个类别的输出转换为概率分布。
- 公式:softmax(xi)=
以上这些激活函数在神经网络中起着至关重要的作用,它们通过添加非线性因素,使得神经网络能够学习和拟合复杂的真实世界系统。
相关文章:

深度学习之激活函数
激活函数的公式根据不同的函数类型而有所不同。以下是一些常见的激活函数及其数学公式: Sigmoid函数: 公式:f(x)特性:输出范围在0到1之间,常用于二分类问题,将输出转换为概率值。但存在梯度消失问题&#…...

OpenStack开源虚拟化平台(一)
目录 一、OpenStack背景介绍(一)OpenStack是什么(二)OpenStack的主要服务 二、计算服务Nova(一)Nova组件介绍(二)Libvirt简介(三)Nova中的RabbitMQ解析 OpenS…...

C++ | Leetcode C++题解之第207题课程表
题目: 题解: class Solution { private:vector<vector<int>> edges;vector<int> indeg;public:bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {edges.resize(numCourses);indeg.resize(numCo…...

vue3中的自定义指令
全局自定义指令 假设我们要创建一个全局指令v-highlight,用于高亮显示元素。这个指令将接受一个颜色参数,并有一个可选的修饰符bold来决定是否加粗文本。 首先,在创建Vue应用时定义这个指令:(这里可以将指令抽离成单…...
)
Postman接口测试工具的原理及应用详解(一)
本系列文章简介: 在当今软件开发的世界中,接口测试作为保证软件质量的重要一环,其重要性不言而喻。随着前后端分离开发模式的普及,接口测试已成为连接前后端开发的桥梁,确保前后端之间的数据交互准确无误。在这样的背景…...

C++ initializer_list类型推导
目录 initializer_list C自动类型推断 auto typeid decltype initializer_list<T> C支持统一初始化{ },出现了一个新的类型initializer_list<T>,一切类型都可以用列表初始化。提供了一种更加灵活、安全和明确的方式来初始化对象。 class…...

造一个交互式3D火山数据可视化
本文由ScriptEcho平台提供技术支持 项目地址:传送门 使用 Plotly.js 创建交互式 3D 火山数据可视化 应用场景 本代码用于将火山数据库中的数据可视化,展示火山的高度、类型和状态。可用于地质学研究、教育和数据探索。 基本功能 该代码使用 Plotly…...

【网络安全】一文带你了解什么是【CSRF攻击】
CSRF(Cross-Site Request Forgery,跨站请求伪造)是一种网络攻击方式,它利用已认证用户在受信任网站上的身份,诱使用户在不知情的情况下执行恶意操作。具体来说,攻击者通过各种方式(如发送恶意链…...

短视频电商源码如何选择
在数字时代的浪潮下,短视频电商以其直观、生动、互动性强的特点,迅速崛起成为电商行业的一股新势力。对于有志于进军短视频电商领域的创业者来说,选择一款合适的短视频电商源码至关重要。本文将从多个角度探讨如何选择短视频电商源码…...

444444
356前期...

初识LangChain的快速入门指南
个人名片 🎓作者简介:java领域优质创作者 🌐个人主页:码农阿豪 📞工作室:新空间代码工作室(提供各种软件服务) 💌个人邮箱:[2435024119qq.com] 📱…...

OpenBayes 教程上新 | CVPR 获奖项目,BioCLlP 快速识别生物种类,再也不会弄混小浣熊和小熊猫了!
市面上有很多植物识别的 App,通过对植物的叶片、花朵、果实等特征进行准确的识别,从而确定植物的种类、名称。但动物识别的 App 却十分有限,这使我们很难区分一些外形相似的动物,例如小浣熊和小熊猫。 左侧为小浣熊,右…...
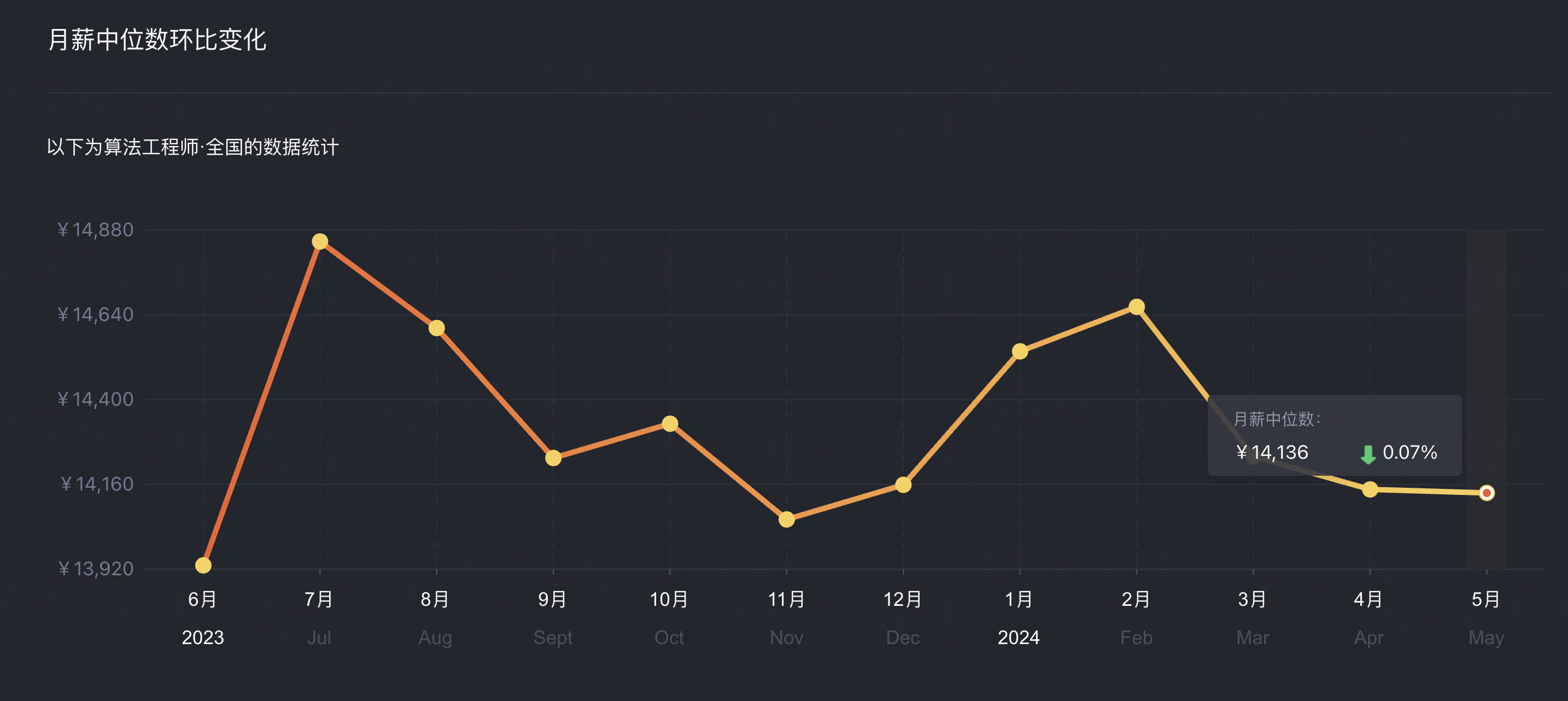
24 年程序员各岗位薪资待遇汇总(最新)
大家好,我是程序员鱼皮。今天分享 24 年 6 月最新的程序员各岗位薪资待遇汇总。 数据是从哪儿来的呢?其实很简单,BOSS 直聘上有一个免费的薪酬查询工具,只要认证成为招聘者就能直接看,便于招聘者了解市场,…...
)
Android SurfaceFlinger——系统动画服务启动(十四)
在了解了 SurfaceFlinger、HWC、OpenGL ES 和 EGL 等相关概念和基础信息后,我们通过系统动画的调用流程引入更多的内容。 一、解析init.rc 开机就启动进程,肯定就要从 rc 文件开始。负责开机动画的进程是 bootanimation。 1、bootanim.rc 源码位置:/frameworks/base/cmds…...

VaRest插件常用节点以及Http请求数据
1.解析json (1)Construct Json Object:构建json对象 (2)Decode Json:解析json 将string转换为json (3)Encode json:将json转换为string (4)Get S…...

【Linux】线程id与互斥(线程三)
上一期我们进行了线程控制的了解与相关操作,但是仍旧有一些问题没有解决 本章第一阶段就是解决tid的问题,第二阶段是进行模拟一个简易线程库(为了加深对于C库封装linux原生线程的理解),第三阶段就是互斥。 目录 线程id…...

JavaEE—什么是服务器?以及Tomcat安装到如何集成到IDEA中?
目录 ▐ 前言 ▐ JavaEE是指什么? ▐ 什么是服务器? ▐ Tomcat安装教程 * 修改服务端口号 ▐ 将Tomcat集成到IDEA中 ▐ 测试 ▐ 结语 ▐ 前言 至此,这半年来我已经完成了JavaSE,Mysql数据库,以及Web前端知识的学习了&am…...

主流分布式消息中间件RabbitMQ、RocketMQ
分布式消息中间件在现代分布式系统中起着至关重要的作用。以下是一些主流的分布式消息中间件: 1. Apache Kafka - 特点:高吞吐量、低延迟、持久化、水平可扩展、分布式日志系统。 - 使用场景:日志收集与处理、实时流处理、事件驱动架构、大数…...
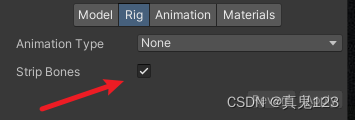
【Unity Linux】模型导致的Unity项目崩溃
模型需勾选Strip Bones。如不勾选,则开启项目崩溃。 也可以删除有问题模型的.meta文件。 (Unity默认会自动勾选,所以不会崩溃) 或打开.meta文件,将optimizeBones的值,由0改为1。(对应面板上的…...

22222
12212...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
