数据结构递归(01)汉诺塔经典问题
说明:使用递归时,必须要遵守两个限制条件:
- 递归存在限制条件,满⾜这个限制条件时,递归不再继续;
- 每次递归调⽤之后越来越接近这个限制条件;
1 汉诺塔(Hanoi Tower)经典问题
1.1 汉诺塔问题描述
汉诺塔(Hanoi Tower)问题是一个经典的递归问题,起源于一个关于印度的传说。问题描述如下:
有一个三脚架,上面有三个从下到上依次递减的圆盘,总共有n个圆盘,这些圆盘最初都放在第一个柱子上,并且每个圆盘上都有不同的大小,使得较大的圆盘不能放在较小的圆盘上面。任务是将所有圆盘从第一个柱子移动到第三个柱子,同时满足以下规则:
- 每次只能移动一个圆盘。
- 每次移动的圆盘必须放在另一个柱子的顶部。
- 任何时候,较大的圆盘不能放在较小的圆盘上面。
1.2 汉诺塔问题分析
汉诺塔问题的分析可以通过递归的方式来理解。下面是针对n=1, n=2, n=3时的步骤说明(其中ABC分别对应第一二三个柱子):
#n=1时:
初始状态 第一步(完成)
A B C A B C
1 0 0 0 0 1 #n=2时:
初始状态 第一步 第二步 第三步(完成)
A B C A B C A B C A B C
1 0 0 0 1 0 0 1 0 0 0 1
2 0 0 2 0 0 0 0 2 0 0 2#n=3时:
说明:由n=2时的状态可知,2个盘从A移动到B或C均是可行的,那么这里我们就将1和2堪称整体。
初始状态 第一步 第二步 第三步(完成)
A B C A B C A B C A B C
1 0 0 0 1 0 0 1 0 0 0 1
2 0 0 0 2 0 0 2 0 0 0 2
3 0 0 3 0 0 0 0 3 0 0 3可以看到,这里的第一步和第三步实际上是使用了n=2时的结论。接下来我们把2 3换成出n-1 n之间的关系。
初始状态 第一步 第二步 第三步(完成)
A B C A B C A B C A B C
1 0 0 0 1 0 0 1 0 0 0 1
2 0 0 0 2 0 0 2 0 0 0 2
3 0 0 0 3 0 0 3 0 0 0 3
... ... ... ...
n 0 0 n 0 0 0 0 n 0 0 n可以看出来,实际上和2与3 的关系是一致的。因此我们使用递归公式的分析进阶思考:
- 对于n个圆盘,将前n-1个圆盘从A柱移动到B柱,使用辅助柱C。
- 将第n个圆盘从A柱移动到C柱。
- 将n-1个圆盘从B柱移动到C柱,使用辅助柱A。
这个递归过程会不断重复,直到所有的圆盘都按照规则成功地移动到目标柱子上。递归的深度是n-1,因为每次移动n-1个圆盘,然后是第n个圆盘,再是n-1个圆盘。总共需要进行2^n - 1次移动才能完成n个圆盘的汉诺塔问题。
1.3 汉诺塔问题 逻辑解决方案
解决汉诺塔问题的方法是递归。对于n个圆盘,解决步骤可以概括为:
- 将上面的n-1个圆盘从起始柱子移动到辅助柱子(不违反规则)。
- 将最大的圆盘(第n个圆盘)从起始柱子移动到目标柱子。
- 将n-1个圆盘从辅助柱子移动到目标柱子(现在最大的圆盘已经在目标柱子上,不违反规则)。
这个过程可以继续递归地应用到n-1个圆盘上,直到n为1,这时问题就变得非常简单,只需将圆盘直接移动到目标柱子上。
2 代码实现
2.1 python代码实现
#!/usr/bin/python3
# -*- coding: UTF-8 -*-def hanoi(n, source, target, auxiliary):if n > 0:# 将n-1个圆盘从source移动到auxiliary,以target作为辅助hanoi(n-1, source, auxiliary, target)# 将第n个圆盘从source移动到targetprint(f"Move disk {n} from {source} to {target}")# 将n-1个圆盘从auxiliary移动到target,以source作为辅助hanoi(n-1, auxiliary, target, source)# 调用函数,将3个圆盘从A柱移动到C柱,B柱作为辅助
hanoi(3, 'A', 'C', 'B')
2.2 C++代码实现
#include <iostream>// 函数声明
void hanoi(int n, char source, char target, char auxiliary);int main() {int numDisks = 3; // 圆盘的数量hanoi(numDisks, 'A', 'C', 'B'); // 将3个圆盘从A柱移动到C柱,B柱作为辅助return 0;
}// 函数定义
void hanoi(int n, char source, char target, char auxiliary) {if (n <= 0) return; // 递归的基本情况// 将n-1个圆盘从source移动到auxiliary,以target作为辅助hanoi(n - 1, source, auxiliary, target);// 将第n个圆盘从source移动到targetstd::cout << "Move disk " << n << " from " << source << " to " << target << std::endl;// 将n-1个圆盘从auxiliary移动到target,以source作为辅助hanoi(n - 1, auxiliary, target, source);
}相关文章:
汉诺塔经典问题)
数据结构递归(01)汉诺塔经典问题
说明:使用递归时,必须要遵守两个限制条件: 递归存在限制条件,满⾜这个限制条件时,递归不再继续; 每次递归调⽤之后越来越接近这个限制条件; 1 汉诺塔(Hanoi Tower)经典…...

计算机专业课面试常见问题-计算机网络篇
目录 1. 计算机网络分为哪 5 层? 2. TCP 协议简述? 3. TCP 和 UDP 的区别?->不同的应用场景? 4. 从浏览器输入网址到显示页…...

HarmonyOS ArkUi ArkWeb加载不出网页问题踩坑
使用 使用还是比较简单的,直接贴代码了 别忘了配置网络权限 Entry Component struct WebPage {State isAttachController: boolean falseState url: string State title: string Prop controller: web_webview.WebviewController new web_webview.WebviewCont…...
微信换手机号了怎么绑定新手机号?
微信换手机号了怎么绑定新手机号? 1、在手机上找到并打开微信; 2、打开微信后,点击底部我的,并进入微信设置; 3、在微信设置账号与安全内,找到手机号并点击进入; 4、选择更换手机号,…...

64.WEB渗透测试-信息收集- WAF、框架组件识别(4)
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 内容参考于: 易锦网校会员专享课 上一个内容:63.WEB渗透测试-信息收集- WAF、框架组件识别(3)-CSDN博客 我们在…...

java.lang.LinkageError: 链接错误的正确解决方法,亲测有效,嘿嘿,有效
文章目录 问题分析报错原因解决思路解决方法(含代码示例)1. 检查类加载器2. 避免在运行时修改类定义3. 更新或修复 JVM4. 检查应用程序的依赖使用 Maven 检查依赖项使用 Gradle 检查依赖项 java.lang.LinkageError 是 Java 虚拟机在尝试链接类定义时发生…...

python最基础
基本的类 python最基础、最常用的类主要有int整形,float浮点型,str字符串,list列表,dict字典,set集合,tuple元组等等。int整形、float浮点型一般用于给变量赋值,tuple元组属于不可变对象&#…...

Python学习路线图(2024最新版)
这是我最开始学Python时的一套学习路线,从入门到上手。(不敢说精通,哈哈~) 一、Python基础知识、变量、数据类型 二、Python条件结构、循环结构 三、Python函数 四、字符串 五、列表与元组 六、字典与集合 最后再送给大家一套免费…...
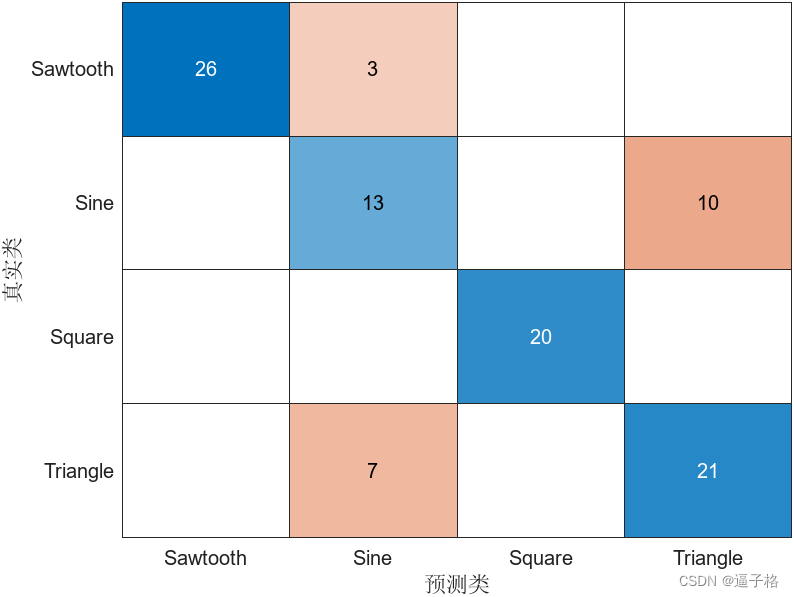
66、基于长短期记忆 (LSTM) 网络对序列数据进行分类
1、基于长短期记忆 (LSTM) 网络对序列数据进行分类的原理及流程 基于长短期记忆(LSTM)网络对序列数据进行分类是一种常见的深度学习任务,适用于处理具有时间或序列关系的数据。下面是在Matlab中使用LSTM网络对序列数据进行分类的基本原理和流…...

RabbitMQ消息可靠性等机制详解(精细版三)
目录 七 RabbitMQ的其他操作 7.1 消息的可靠性(发送可靠) 7.1.1 confim机制(保证发送可靠) 7.1.2 Return机制(保证发送可靠) 7.1.3 编写配置文件 7.1.4 开启Confirm和Return 7.2 手动Ack(保证接收可靠) 7.2.1 添加配置文件 7.2.2 手动ack 7.3 避免消息重复消费 7.3.…...

88888
49615...

深度学习之激活函数
激活函数的公式根据不同的函数类型而有所不同。以下是一些常见的激活函数及其数学公式: Sigmoid函数: 公式:f(x)特性:输出范围在0到1之间,常用于二分类问题,将输出转换为概率值。但存在梯度消失问题&#…...

OpenStack开源虚拟化平台(一)
目录 一、OpenStack背景介绍(一)OpenStack是什么(二)OpenStack的主要服务 二、计算服务Nova(一)Nova组件介绍(二)Libvirt简介(三)Nova中的RabbitMQ解析 OpenS…...

C++ | Leetcode C++题解之第207题课程表
题目: 题解: class Solution { private:vector<vector<int>> edges;vector<int> indeg;public:bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {edges.resize(numCourses);indeg.resize(numCo…...

vue3中的自定义指令
全局自定义指令 假设我们要创建一个全局指令v-highlight,用于高亮显示元素。这个指令将接受一个颜色参数,并有一个可选的修饰符bold来决定是否加粗文本。 首先,在创建Vue应用时定义这个指令:(这里可以将指令抽离成单…...
)
Postman接口测试工具的原理及应用详解(一)
本系列文章简介: 在当今软件开发的世界中,接口测试作为保证软件质量的重要一环,其重要性不言而喻。随着前后端分离开发模式的普及,接口测试已成为连接前后端开发的桥梁,确保前后端之间的数据交互准确无误。在这样的背景…...

C++ initializer_list类型推导
目录 initializer_list C自动类型推断 auto typeid decltype initializer_list<T> C支持统一初始化{ },出现了一个新的类型initializer_list<T>,一切类型都可以用列表初始化。提供了一种更加灵活、安全和明确的方式来初始化对象。 class…...

造一个交互式3D火山数据可视化
本文由ScriptEcho平台提供技术支持 项目地址:传送门 使用 Plotly.js 创建交互式 3D 火山数据可视化 应用场景 本代码用于将火山数据库中的数据可视化,展示火山的高度、类型和状态。可用于地质学研究、教育和数据探索。 基本功能 该代码使用 Plotly…...

【网络安全】一文带你了解什么是【CSRF攻击】
CSRF(Cross-Site Request Forgery,跨站请求伪造)是一种网络攻击方式,它利用已认证用户在受信任网站上的身份,诱使用户在不知情的情况下执行恶意操作。具体来说,攻击者通过各种方式(如发送恶意链…...

短视频电商源码如何选择
在数字时代的浪潮下,短视频电商以其直观、生动、互动性强的特点,迅速崛起成为电商行业的一股新势力。对于有志于进军短视频电商领域的创业者来说,选择一款合适的短视频电商源码至关重要。本文将从多个角度探讨如何选择短视频电商源码…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...
