排序题目:多数元素 II
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 进阶
- 前言
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
- 解法三
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:多数元素 II
出处:229. 多数元素 II
难度
3 级
题目描述
要求
给定大小为 n \texttt{n} n 的数组 nums \texttt{nums} nums,找出其中所有出现超过 ⌊ n 3 ⌋ \Big\lfloor \dfrac{\texttt{n}}{\texttt{3}} \Big\rfloor ⌊3n⌋ 次的元素。
示例
示例 1:
输入: nums = [3,2,3] \texttt{nums = [3,2,3]} nums = [3,2,3]
输出: [3] \texttt{[3]} [3]
示例 2:
输入: nums = [1] \texttt{nums = [1]} nums = [1]
输出: [1] \texttt{[1]} [1]
示例 3:
输入: nums = [1,2] \texttt{nums = [1,2]} nums = [1,2]
输出: [1,2] \texttt{[1,2]} [1,2]
数据范围
- n = nums.length \texttt{n} = \texttt{nums.length} n=nums.length
- 1 ≤ n ≤ 5 × 10 4 \texttt{1} \le \texttt{n} \le \texttt{5} \times \texttt{10}^\texttt{4} 1≤n≤5×104
- -10 9 ≤ nums[i] ≤ 10 9 \texttt{-10}^\texttt{9} \le \texttt{nums[i]} \le \texttt{10}^\texttt{9} -109≤nums[i]≤109
进阶
你可以使用线性时间复杂度和 O(1) \texttt{O(1)} O(1) 空间复杂度解决此问题吗?
前言
这道题是「多数元素」的进阶,要求找出数组中所有出现次数大于 ⌊ n 3 ⌋ \Big\lfloor \dfrac{n}{3} \Big\rfloor ⌊3n⌋ 的元素。这道题也可以使用哈希表计数、排序和摩尔投票三种解法得到答案。
长度是 n n n 的数组中,最多有 2 2 2 个出现次数大于 ⌊ n 3 ⌋ \Big\lfloor \dfrac{n}{3} \Big\rfloor ⌊3n⌋ 的元素。可以使用反证法证明。
假设有 3 3 3 个出现次数大于 ⌊ n 3 ⌋ \Big\lfloor \dfrac{n}{3} \Big\rfloor ⌊3n⌋ 的元素,这 3 3 3 个元素的出现次数都不小于 ⌊ n 3 ⌋ + 1 \Big\lfloor \dfrac{n}{3} \Big\rfloor + 1 ⌊3n⌋+1,因此这 3 3 3 个元素的总出现次数至少为 3 × ⌊ n 3 ⌋ + 3 3 \times \Big\lfloor \dfrac{n}{3} \Big\rfloor + 3 3×⌊3n⌋+3。由于 ⌊ n 3 ⌋ > n 3 − 1 \Big\lfloor \dfrac{n}{3} \Big\rfloor > \dfrac{n}{3} - 1 ⌊3n⌋>3n−1,因此 3 × ⌊ n 3 ⌋ + 3 > 3 × ( n 3 − 1 ) + 3 = 3 × n 3 − 3 + 3 = n 3 \times \Big\lfloor \dfrac{n}{3} \Big\rfloor + 3 > 3 \times (\dfrac{n}{3} - 1) + 3 = 3 \times \dfrac{n}{3} - 3 + 3 = n 3×⌊3n⌋+3>3×(3n−1)+3=3×3n−3+3=n,即这 3 3 3 个元素的总出现次数一定超过 n n n,和数组长度是 n n n 矛盾。因此数组中不可能有 3 3 3 个出现次数大于 ⌊ n 3 ⌋ \Big\lfloor \dfrac{n}{3} \Big\rfloor ⌊3n⌋ 的元素,最多有 2 2 2 个出现次数大于 ⌊ n 3 ⌋ \Big\lfloor \dfrac{n}{3} \Big\rfloor ⌊3n⌋ 的元素。
解法一
思路和算法
最直观的解法是统计数组中每个元素的出现次数,然后寻找出现次数大于 ⌊ n 3 ⌋ \Big\lfloor \dfrac{n}{3} \Big\rfloor ⌊3n⌋ 的元素。
遍历数组,使用哈希表记录每个元素的出现次数,遍历结束之后即可得到数组中每个元素的出现次数。然后遍历哈希表,对于哈希表中的每个元素得到出现次数,将出现次数大于 ⌊ n 3 ⌋ \Big\lfloor \dfrac{n}{3} \Big\rfloor ⌊3n⌋ 的元素添加到结果中。
代码
class Solution {public List<Integer> majorityElement(int[] nums) {Map<Integer, Integer> counts = new HashMap<Integer, Integer>();for (int num : nums) {counts.put(num, counts.getOrDefault(num, 0) + 1);}List<Integer> majorities = new ArrayList<Integer>();int n = nums.length;Set<Integer> set = counts.keySet();for (int num : set) {if (counts.get(num) > n / 3) {majorities.add(num);}}return majorities;}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是数组 nums \textit{nums} nums 的长度。遍历数组统计每个元素的出现次数需要 O ( n ) O(n) O(n) 的时间,遍历哈希表得到多数元素也需要 O ( n ) O(n) O(n) 的时间。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是数组 nums \textit{nums} nums 的长度。需要创建哈希表记录每个元素的出现次数,哈希表中的元素个数不超过 n n n。
解法二
思路和算法
首先将数组排序,排序后的数组满足相等的元素一定出现在数组中的相邻位置。如果一个元素在数组中的出现次数大于 ⌊ n 3 ⌋ \Big\lfloor \dfrac{n}{3} \Big\rfloor ⌊3n⌋,则排序后的数组中存在至少 ⌊ n 3 ⌋ + 1 \Big\lfloor \dfrac{n}{3} \Big\rfloor + 1 ⌊3n⌋+1 个连续的元素都等于该元素,即一定存在两个差为 ⌊ n 3 ⌋ \Big\lfloor \dfrac{n}{3} \Big\rfloor ⌊3n⌋ 的下标处的元素都等于该元素。
将数组 nums \textit{nums} nums 排序之后遍历数组 nums \textit{nums} nums,对于下标 i i i,当 i ≥ ⌊ n 3 ⌋ i \ge \Big\lfloor \dfrac{n}{3} \Big\rfloor i≥⌊3n⌋ 时,如果 nums [ i ] = nums [ i − ⌊ n 3 ⌋ ] \textit{nums}[i] = \textit{nums}[i - \Big\lfloor \dfrac{n}{3} \Big\rfloor] nums[i]=nums[i−⌊3n⌋],则 nums [ i ] \textit{nums}[i] nums[i] 是出现次数大于 ⌊ n 3 ⌋ \Big\lfloor \dfrac{n}{3} \Big\rfloor ⌊3n⌋ 的元素。
为了避免重复计算,当 i < n − 1 i < n - 1 i<n−1 且 nums [ i ] = nums [ i + 1 ] \textit{nums}[i] = \textit{nums}[i + 1] nums[i]=nums[i+1] 时跳过下标 i i i,只有当下标 i i i 的右侧没有与 nums [ i ] \textit{nums}[i] nums[i] 相等的元素时才判断 nums [ i ] = nums [ i − ⌊ n 3 ⌋ ] \textit{nums}[i] = \textit{nums}[i - \Big\lfloor \dfrac{n}{3} \Big\rfloor] nums[i]=nums[i−⌊3n⌋] 是否成立,如果成立则将 nums [ i ] \textit{nums}[i] nums[i] 添加到结果中。
代码
class Solution {public List<Integer> majorityElement(int[] nums) {Arrays.sort(nums);List<Integer> majorities = new ArrayList<Integer>();int n = nums.length;for (int i = n / 3; i < n; i++) {int num = nums[i];if (i < n - 1 && num == nums[i + 1]) {continue;}if (num == nums[i - n / 3]) {majorities.add(num);}}return majorities;}
}
复杂度分析
-
时间复杂度: O ( n log n ) O(n \log n) O(nlogn),其中 n n n 是数组 nums \textit{nums} nums 的长度。排序需要 O ( n log n ) O(n \log n) O(nlogn) 的时间。
-
空间复杂度: O ( log n ) O(\log n) O(logn),其中 n n n 是数组 nums \textit{nums} nums 的长度。排序需要 O ( log n ) O(\log n) O(logn) 的递归调用栈空间。
解法三
思路和算法
原始的摩尔投票算法用于找到出现次数大于一半的元素,其时间复杂度是 O ( n ) O(n) O(n),空间复杂度是 O ( 1 ) O(1) O(1)。摩尔投票算法可以推广到寻找出现次数大于 ⌊ n k ⌋ \Big\lfloor \dfrac{n}{k} \Big\rfloor ⌊kn⌋ 的元素,其中 k k k 是大于 1 1 1 的正整数。
由于出现次数大于 ⌊ n 3 ⌋ \Big\lfloor \dfrac{n}{3} \Big\rfloor ⌊3n⌋ 的元素不可能超过 2 2 2 个,因此维护 2 2 2 个候选元素 majority 1 \textit{majority}_1 majority1 和 majority 2 \textit{majority}_2 majority2,以及两个候选元素的出现次数 count 1 \textit{count}_1 count1 和 count 2 \textit{count}_2 count2,初始时候选元素和出现次数都是 0 0 0。
遍历数组,当遍历到元素 num \textit{num} num 时,执行如下操作。
-
比较 num \textit{num} num 是否和候选元素相等,如果相等则将相应的出现次数加 1 1 1。
-
如果 num = majority 1 \textit{num} = \textit{majority}_1 num=majority1,则将 count 1 \textit{count}_1 count1 加 1 1 1。
-
否则,如果 num = majority 2 \textit{num} = \textit{majority}_2 num=majority2,则将 count 2 \textit{count}_2 count2 加 1 1 1。
-
-
如果 num \textit{num} num 和两个候选元素都不相等,则判断两个候选元素的出现次数是否为 0 0 0,如果为 0 0 0 则更新候选元素和出现次数。
-
如果 count 1 = 0 \textit{count}_1 = 0 count1=0,则将 majority 1 \textit{majority}_1 majority1 更新为 num \textit{num} num,并将 count 1 \textit{count}_1 count1 加 1 1 1。
-
否则,如果 count 2 = 0 \textit{count}_2 = 0 count2=0,则将 majority 2 \textit{majority}_2 majority2 更新为 num \textit{num} num,并将 count 2 \textit{count}_2 count2 加 1 1 1。
-
-
如果 num \textit{num} num 和两个候选元素都不相等且两个候选元素的出现次数都大于 0 0 0,则 num \textit{num} num 和两个候选元素抵消,将 count 1 \textit{count}_1 count1 和 count 2 \textit{count}_2 count2 都减 1 1 1。
遍历结束之后,得到两个候选元素。再次遍历数组,统计两个候选元素在数组中的出现次数,当出现次数大于 ⌊ n 3 ⌋ \Big\lfloor \dfrac{n}{3} \Big\rfloor ⌊3n⌋ 时将候选元素添加到结果中。
代码
class Solution {public List<Integer> majorityElement(int[] nums) {int majority1 = 0, majority2 = 0;int count1 = 0, count2 = 0;for (int num : nums) {if (num == majority1) {count1++;} else if (num == majority2) {count2++;} else if (count1 == 0) {majority1 = num;count1++;} else if (count2 == 0) {majority2 = num;count2++;} else {count1--;count2--;}}count1 = 0;count2 = 0;for (int num : nums) {if (num == majority1) {count1++;} else if (num == majority2) {count2++;}}List<Integer> majorities = new ArrayList<Integer>();int n = nums.length;if (count1 > n / 3) {majorities.add(majority1);}if (count2 > n / 3) {majorities.add(majority2);}return majorities;}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是数组 nums \textit{nums} nums 的长度。需要遍历数组 nums \textit{nums} nums 两次。
-
空间复杂度: O ( 1 ) O(1) O(1)。
相关文章:

排序题目:多数元素 II
文章目录 题目标题和出处难度题目描述要求示例数据范围进阶 前言解法一思路和算法代码复杂度分析 解法二思路和算法代码复杂度分析 解法三思路和算法代码复杂度分析 题目 标题和出处 标题:多数元素 II 出处:229. 多数元素 II 难度 3 级 题目描述 …...

<电力行业> - 《第1课:电力行业的五大四小》
1 什么是电力行业的五大四小? 我们常说的电力行业的五大四小,指的是电力行业有实力的公司,分为:较强梯队的五大集团、较弱梯队的四小豪门。 五个实力雄厚的集团,分别是: 中国华能集团公司中国大唐集团公…...

数据库定义语言(DDL)
数据库定义语言(DDL) 一、数据库操作 1、 查询所有的数据库 SHOW DATABASES;效果截图: 2、使用指定的数据库 use 2403 2403javaee;效果截图: 3、创建数据库 CREATE DATABASE 2404javaee;效果截图: 4、删除数据…...

mybatis实现多表查询
mybatis高级查询【掌握】 1、准备工作 【1】包结构 创建java项目,导入jar包和log4j日志配置文件以及连接数据库的配置文件; 【2】导入SQL脚本 运行资料中的sql脚本:mybatis.sql 【3】创建实体来包,导入资料中的pojo 【4】User…...

数据结构:队列详解 c++信息学奥赛基础知识讲解
目录 一、队列概念 二、队列容器 三、队列操作 四、代码实操 五、队列遍历 六、案例实操 题目描述: 输入格式: 输出格式: 输入样例: 输出样例: 详细代码: 一、队列概念 队列是一种特殊的线性…...
硬件开发笔记(二十三):贴片电阻的类别、封装介绍,AD21导入贴片电阻原理图封装库3D模型
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/140110514 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...
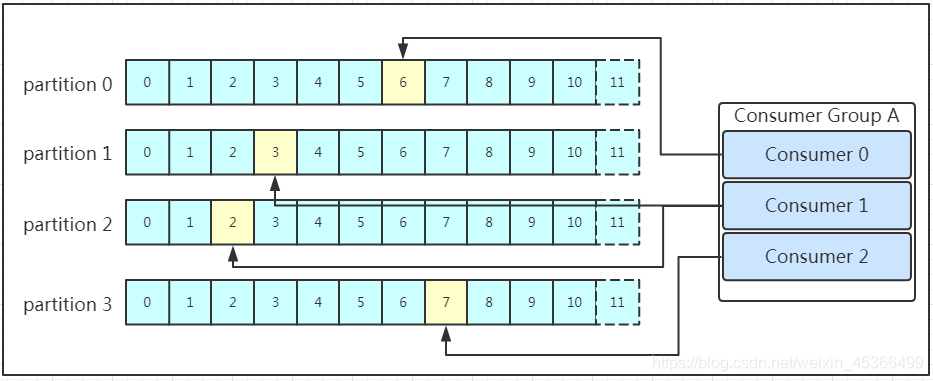
Kafka基本原理详解
(一)概念理解 Apache Kafka是一种开源的分布式流处理平台,专为高性能、高吞吐量的实时数据处理而设计。它最初由LinkedIn公司开发,旨在解决其网站活动中产生的大量实时数据处理和传输问题,后来于2011年开源࿰…...
关卡编辑器之剧情编辑)
【Unity】RPG2D龙城纷争(七)关卡编辑器之剧情编辑
更新日期:2024年7月1日。 项目源码:第五章发布(正式开始游戏逻辑的章节) 索引 简介一、剧情编辑1.对话数据集2.对话触发方式3.选择对话角色4.设置对话到关卡5.通关条件简介 严格来说,剧情编辑不在关卡编辑器界面中完成,只不过它仍然属于关卡编辑的范畴。 在我们的设想中…...

uniapp启动页面鉴权页面闪烁问题
在使用uni-app开发app 打包完成后如果没有token,那么就在onLaunch生命周期里面判断用户是否登录并跳转至登录页。 但是在app中页面会先进入首页然后再跳转至登录页,十分影响体验。 处理方法: 使用plus.navigator.closeSplashscreen() 官网…...

全志H616交叉编译工具链的安装与使用
交叉编译的概念 1. 什么是交叉编译? 交叉编译是指在一个平台上生成可以在另一个平台上运行的可执行代码。例如,在Ubuntu Linux上编写代码,并编译生成可在Orange Pi Zero2上运行的可执行文件。这个过程是通过使用一个专门的交叉编译工具链来…...
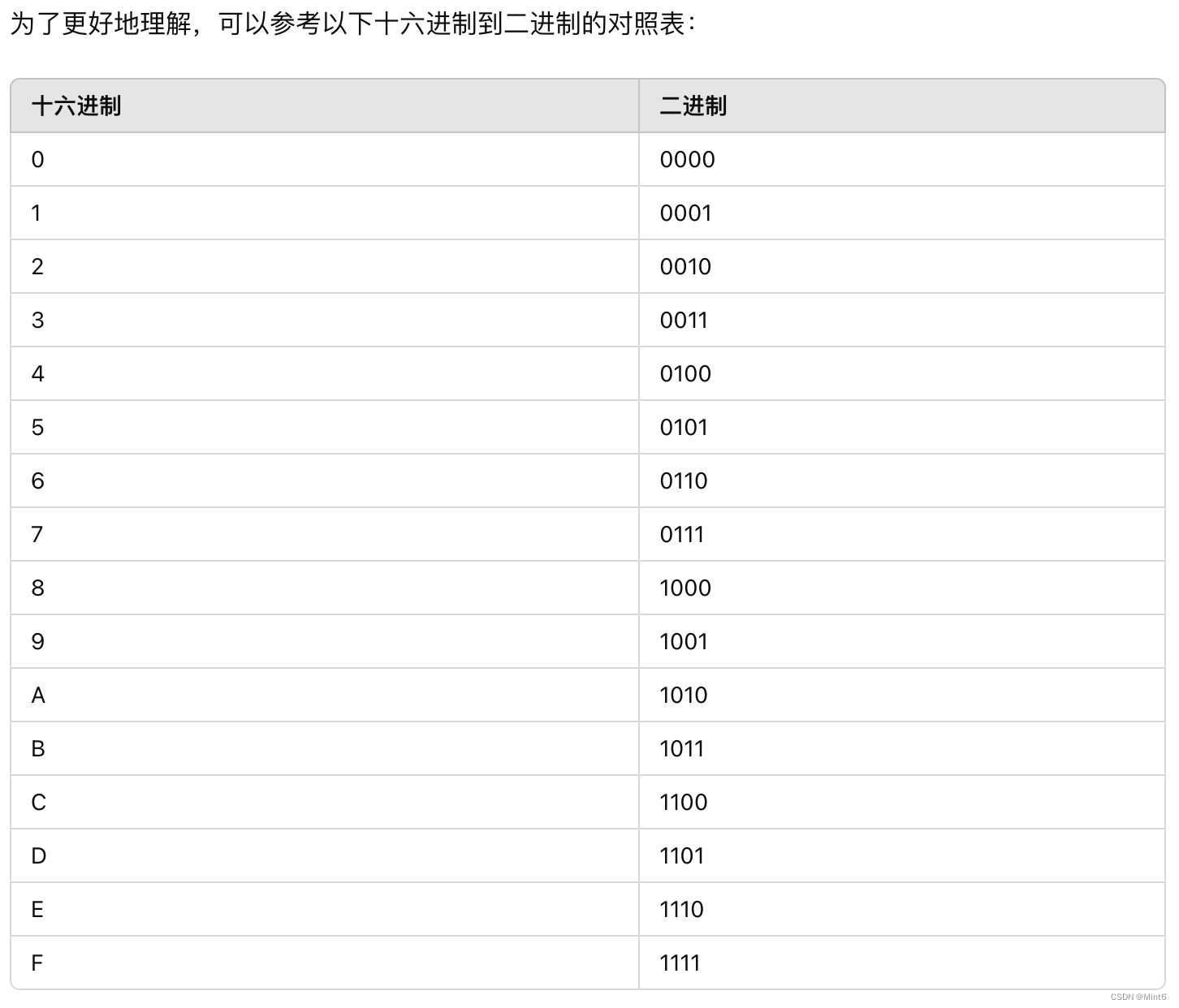
深入解析Java和Go语言中String与byte数组的转换原理
1.Java String与byte[]互相转换存在的问题 java中,按照byte[] 》string 》byte[]的流程转换后,byte数据与最初的byte不一致。 多说无益,上代码,本地macos机器执行,统一使用的UTF-8编码。 import java.nio.charset.S…...

什么是strcmp函数
目录 开头1.什么是strcmp函数2.strcmp函数里的内部结构3.strcmp函数的实际运用(这里只列举其一)脑筋急转弯 结尾 开头 大家好,我叫这是我58。今天,我们要来认识一下C语言中的strcmp函数。 1.什么是strcmp函数 strcmp函数来自于C语言中的头文件<str…...

Follow Carl To Grow|【LeetCode】491.递增子序列,46.全排列,47.全排列 II
【LeetCode】491.递增子序列 题意:给你一个整数数组 nums ,找出并返回所有该数组中不同的递增子序列,递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。 数组中可能含有重复元素,如出现两个整数相等,也可以…...

pytorch nn.Embedding 用法和原理
nn.Embedding 是 PyTorch 中的一个模块,用于将离散的输入(通常是词或子词的索引)映射到连续的向量空间。它在自然语言处理和其他需要处理离散输入的任务中非常常用。以下是 nn.Embedding 的用法和原理。 用法 初始化 nn.Embedding nn.Embed…...

Python中常用的有7种值(数据)的类型及type()语句的用法
目录 0.Python中常用的有7种值(数据)的类型Python中的数据类型主要有:Number(数字)、Boolean(布尔)、String(字符串)、List(列表)、Tuple…...
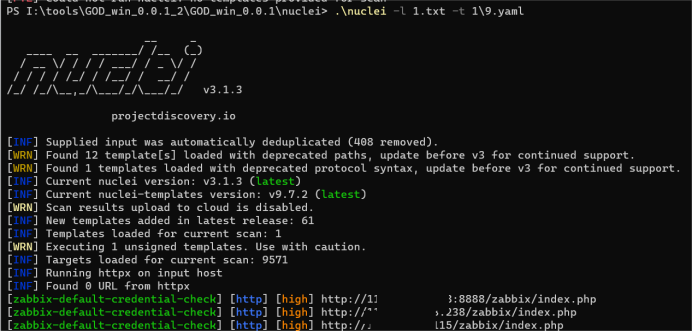
某配送平台未授权访问和弱口令(附赠nuclei默认密码验证脚本)
找到一个某src的子站,通过信息收集插件,发现ZABBIX-监控系统,可以日一下 使用谷歌搜索历史漏洞:zabbix漏洞 通过目录扫描扫描到后台,谷歌搜索一下有没有默认弱口令 成功进去了,挖洞就是这么简单 搜索文章还…...

01.总览
目录 简介Course 1: Natural Language Processing with Classification and Vector SpaceWeek 1: Sentiment Analysis with Logistic RegressionWeek 2: Sentiment Analysis with Nave BayesWeek 3: Vector Space ModelsWeek 4: Machine Translation and Document Search Cours…...
Linux换源
前言 安装完Linux系统,尽量更换源以提高安装软件的速度。 步骤 备份原始源列表sudo cp /etc/apt/sources.list /etc/apt/sources.list.bak修改sources.list sudo vim /etc/apt/sources.list将内容替换成对应的源 **PS:清华源地址:https:…...

【高考志愿】 化学工程与技术
目录 一、专业概述 二、就业前景 三、就业方向 四、报考注意 五、专业发展与深造 六、化学工程与技术专业排名 七、总结 一、专业概述 化学工程与技术专业,这是一门深具挑战与机遇的综合性学科。它融合了工程技术的实用性和化学原理的严谨性,为毕…...

2024上半年网络与数据安全法规政策、国标、报告合集
事关大局,我国数据安全立法体系已基本形成并逐步细化。数据基础制度建设事关国家发展和安全大局,数据安全治理贯穿构建数据基础制度体系全过程。随着我国数字经济建设进程加快,数据安全立法实现由点到面、由面到体加速构建,目前已…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...
