数据结构之“刷链表题”

                                                🌹个人主页🌹：喜欢草莓熊的bear

                                                       🌹专栏🌹：数据结构

目录

前言

一、相交链表

题目链接

大致思路

代码实现

二、环形链表1

题目链接

大致思路

代码实现

三、环形链表2

题目链接

大致思路

代码实现

总结

---

---

前言

通过一些例题来复习一下之前学习的链表。

一、相交链表

题目链接

相交链表

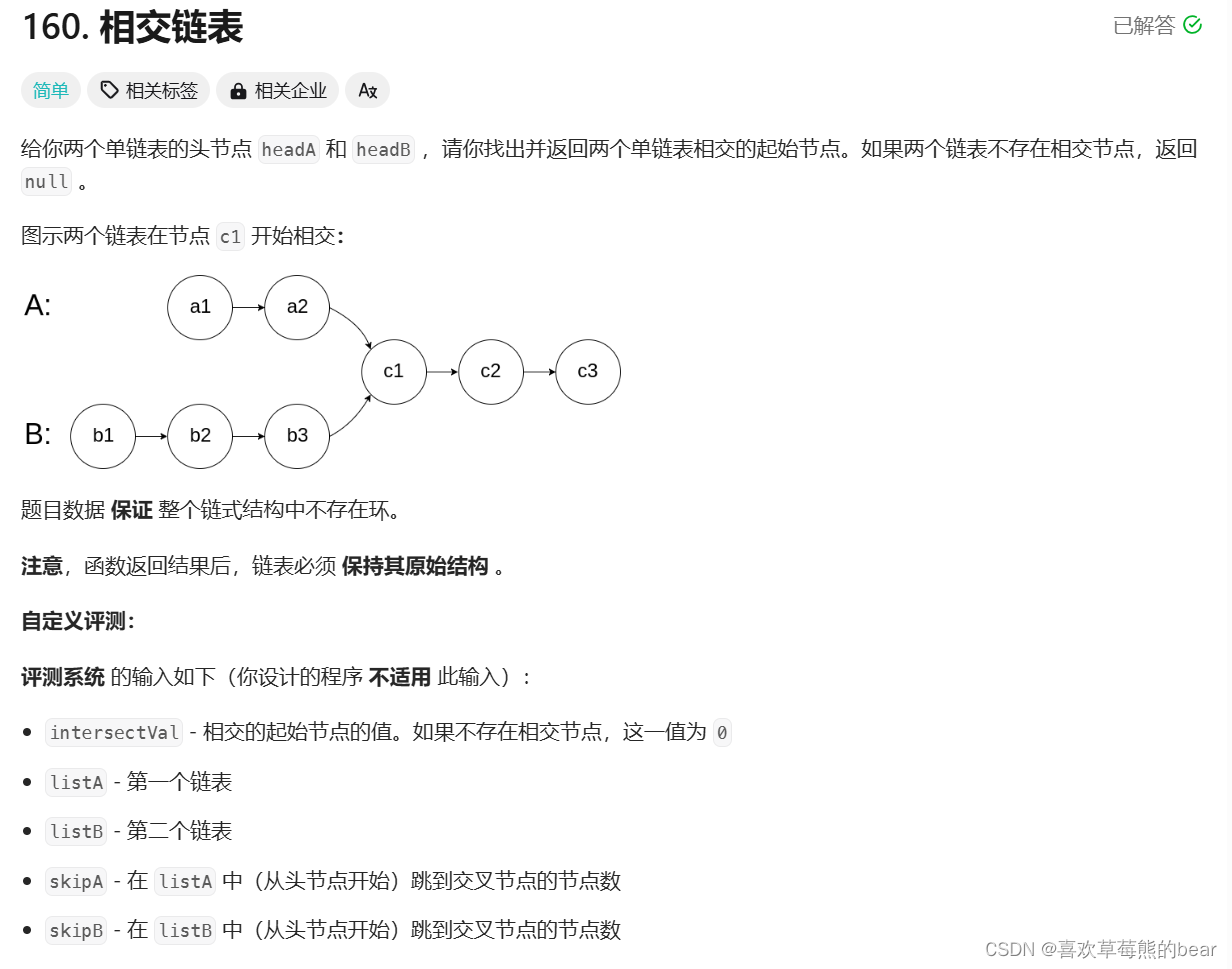
大致思路

用两个指针来遍历两个链表，存在相同则就有相交（注意这里相同的地址或者是指针相同，不可以判断指针里面的值是否相同）。我们要让两个表在相同位置进行遍历、找相同操作。很简单我们用计数操作来计入链表长度，让长的走了距离差，再让他们同时走。这里计算距离差我们要调用一下绝对值函数（abs）。代码里面还运用了假设法，假设谁为长链表，假设不成立就调换一下就可以了，这里假设法值得体会一下。

代码实现

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) 
{struct ListNode* curA = headA;struct ListNode* curB = headB;int A=0;int B=0;while(curA->next){curA=curA->next;A++;}while(curB->next){curB=curB->next;B++;}if(curA!=curB){return NULL;}int juli = abs(A-B);struct ListNode* llong = headA;struct ListNode* sshort = headB;if(A<B){llong = headB;sshort = headA;}while(juli--){llong=llong->next;}while(llong!=sshort){llong=llong->next;sshort=sshort->next;}return llong;
}

二、环形链表1

题目链接

环形链表1

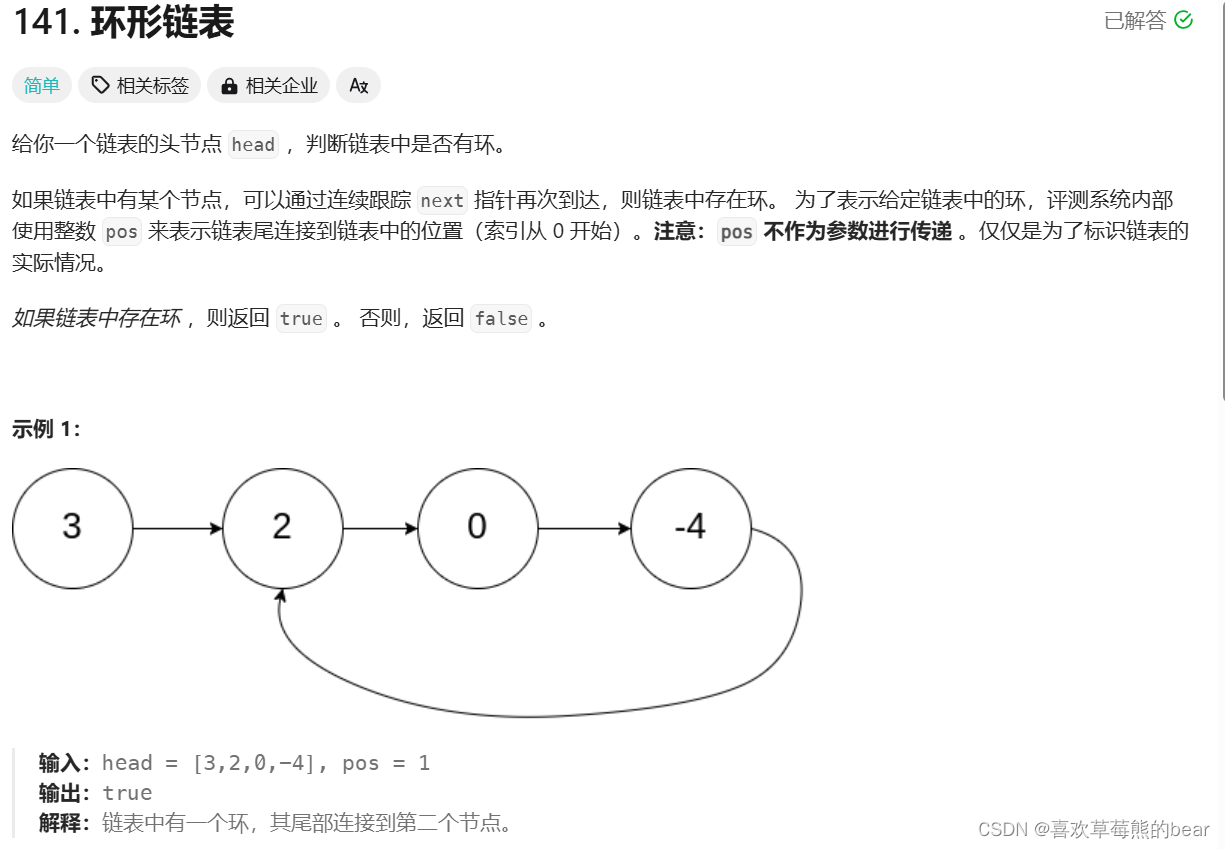
大致思路

本地要求我们判断是否是一个带环链表，带环会存在循环，用快慢指针来解决这题。fast指针走两步，slow走一步。他们会相遇吗？我画图证明一下：我这里证明的是fast走两步，slow走一步的情况，其他情况大家可以尝试证明。

结论带环了一定会相遇，代码实现很简单。

代码实现

bool hasCycle(struct ListNode *head) 
{struct ListNode *fast=head;struct ListNode *slow=head;while(fast && fast->next){fast=fast->next->next;slow=slow->next;if(slow == fast){return true;}}return false;
}

三、环形链表2

题目链接

环形链表2

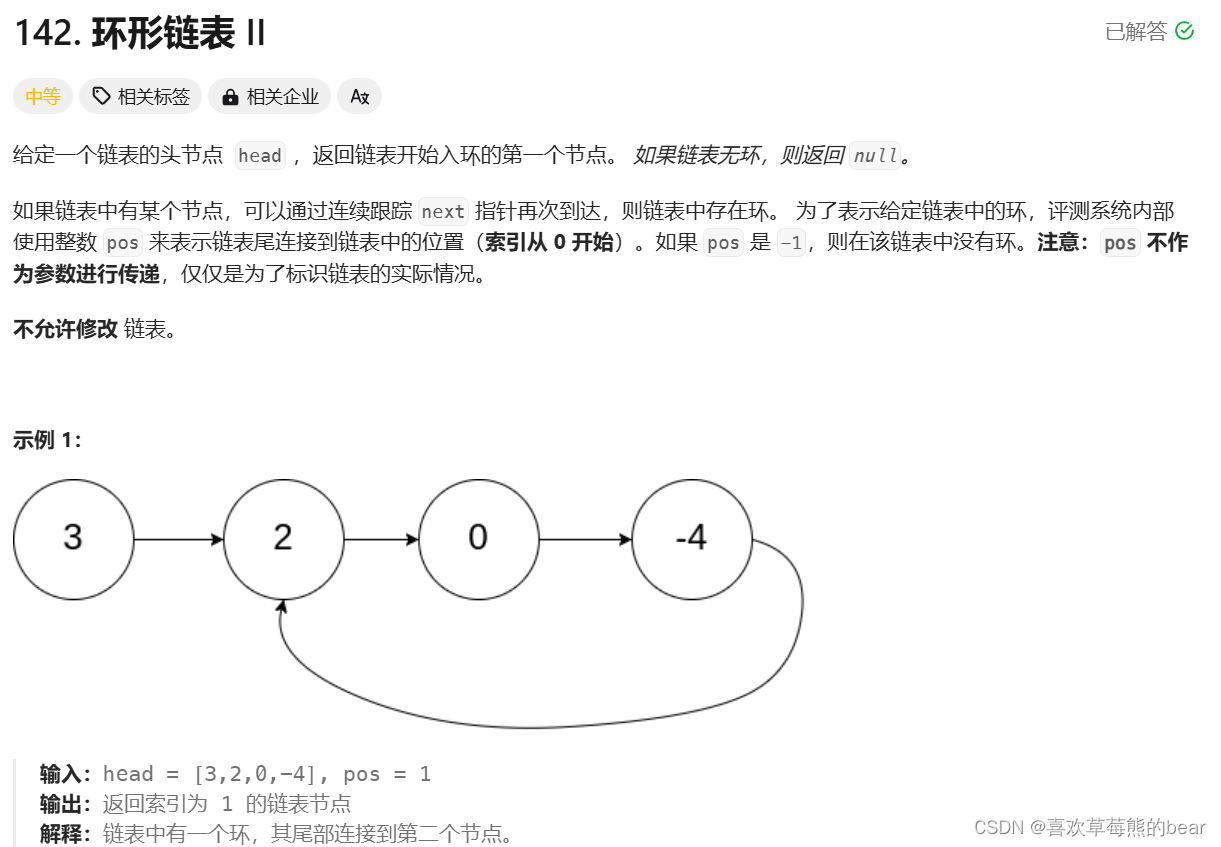
 基于带环链表衍生出来的，先判断是否带环，带环了还要返回入环的第一个节点。

大致思路

与上一题环形链表相似，还要返回第一个入环节点。这里先给上一个结论，让相遇指针的下一个节点和头指针同时走他们就会在第一入环的节点相遇。我们看作一个相交链表返回相交节点的问题来做，直接调用前面写的函数就可以了。    让我来证明一下

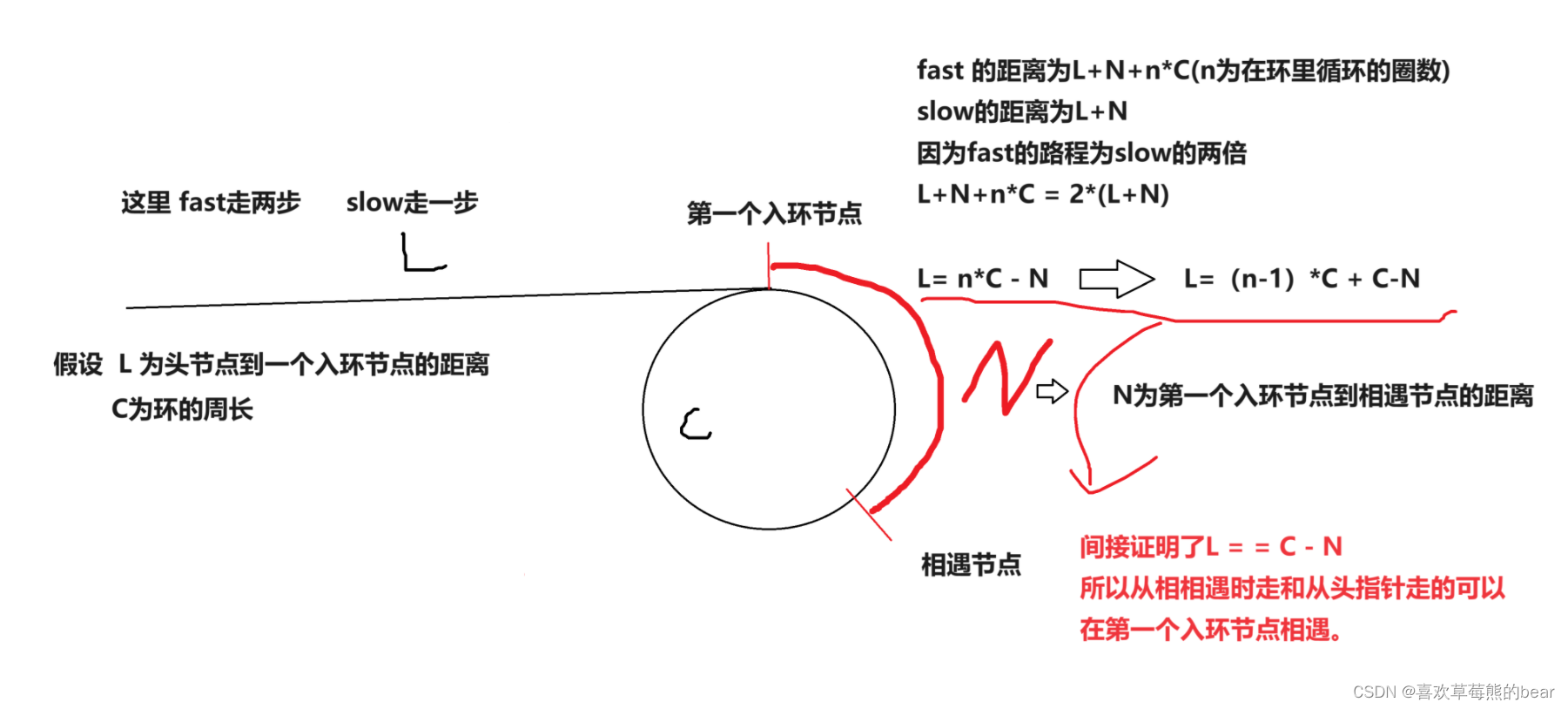
 运用了一下数学公式等到关系式证明了。

代码实现

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) 
{struct ListNode* curA = headA;struct ListNode* curB = headB;int A=0;int B=0;while(curA->next){curA=curA->next;A++;}while(curB->next){curB=curB->next;B++;}if(curA!=curB){return NULL;}int juli = abs(A-B);struct ListNode* llong = headA;struct ListNode* sshort = headB;if(A<B){llong = headB;sshort = headA;}while(juli--){llong=llong->next;}while(llong!=sshort){llong=llong->next;sshort=sshort->next;}return llong;
}
struct ListNode *detectCycle(struct ListNode *head) 
{struct ListNode *fast=head;struct ListNode *slow=head;while(fast && fast->next){fast=fast->next->next;slow=slow->next;if(slow == fast){struct ListNode* newnode = slow->next;slow->next=NULL;return getIntersectionNode(head,newnode);}}return NULL;
}

---

总结

这些都题还不错，值得我们掌握。加油加油，请持续关注bear！！🌹🌹