面向阿克曼移动机器人(自行车模型)的LQR(最优二次型调节器)路径跟踪方法
线性二次调节器(Linear Quadratic Regulator,LQR)是针对线性系统的最优控制方法。LQR 方法标准的求解体系是在考虑到损耗尽可能小的情况下, 以尽量小的代价平衡其他状态分量。一般情况下,线性系统在LQR 控制方法中用状态空间方程描述,性能能指标函数由二次型函数描述。
LQR 方法存在以下优点:
- 最小能量消耗和最高路径跟踪精度。
- 求解时能够考虑多状态情况。
- 鲁棒性较强。
缺点:
- 控制效果和模型精确程度有很大相关性。
- 实时计算状态反馈矩阵和控制增益。
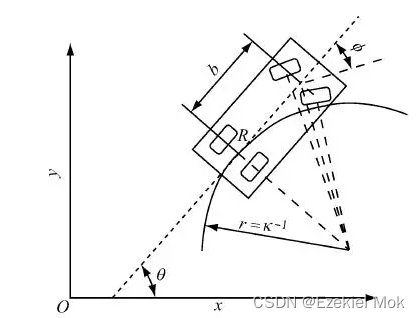
一、系统模型
1.1 车辆模型
一般来说阿克曼移动机器人可以简化为自行车模型,是一个非线性时变系统,工程上一般通过在平衡点附近差分线性化转化为线性系统来分析和控制,具体就不推导了,我直接给出模型。
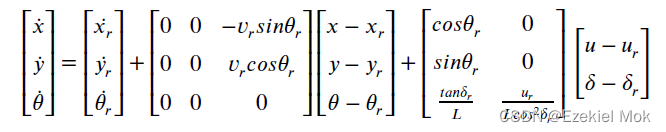
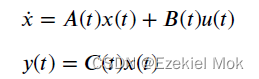
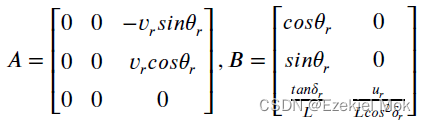
1.2 线性系统状态反馈控制示意图
状态反馈是线性能控线性系统镇定的一个有效方法,主要是通过极点配置方法寻找一组非正的闭环极点使得闭环系统大范围渐进稳定。
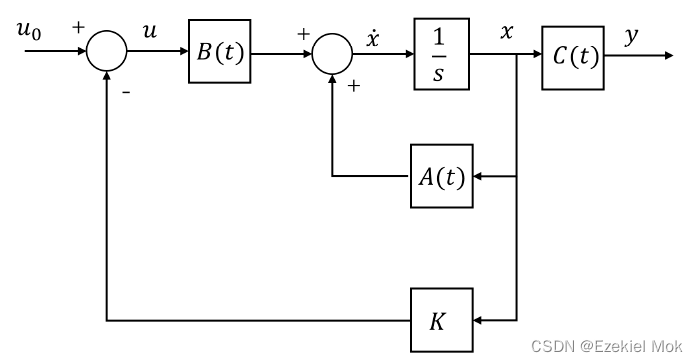
A,B,C分别代表系统矩阵、输入矩阵和输出矩阵,K是待设计的状态反馈增益。
二、控制器设计
2.1 代价函数泛函设计
最优控制里,代价函数一般设计为控制性能和控制代价的范数加权和,形式如下
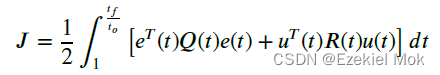
其中,期望和实际的误差系统定义为
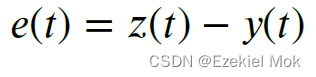
2.2 最优状态反馈控制律推导
当想要状态与期望状态之间的误差越差越小,同时控制消耗更少的能量。求解极小值点时,新定义拉格朗日函数如下
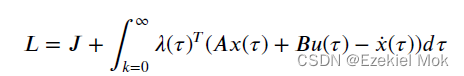
在拉格朗日函数基础上对各个优化变量的一阶导为零 ,得
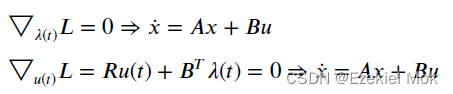
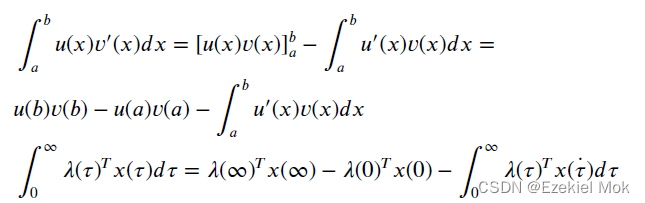
当时候,
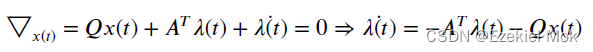
推导LQR控制律时候,设 ,求偏导后可得
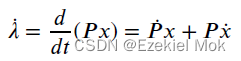
由![]() 得
得
![]()
由于状态量初始不为零,只能是
![]()
又由于当上述方程成立时候,收敛到了期望的范围 ,
为零,因此得到立卡提方程形式的矩阵微分方程
![]()
综上,通过迭代或者近似方法求解上述立卡提方程后,最优的控制律为
![]()
2.3 连续立卡提方程求解流程
三、具体实现代码
3.1 main函数
close all
clear;
clc;
cx = [];
cy= [];
y0 = @(t_step) 10*sin(2 * t_step + 1);
x0_dot= @(t_step) 5 * 2 * cos(2 * t_step + 1);
x0 = @(t_step) -40*cos(t_step + 0.5);
for theta=0:pi/200:2*picx(end + 1) = x0(theta);cy(end + 1) = y0(theta);
end
refer_path_primary= [cx', cy'];
x = refer_path_primary(:, 1)';
y = refer_path_primary(:, 2)';
points = [x; y]';
ds = 0.1 ;%等距插值处理的间隔
distance = [0, cumsum(hypot(diff(x, 1), diff(y, 1)))]';
distance_specific = 0:ds:distance(end);
hypot(diff(x, 1), diff(y, 1));
diff(x, 1);
diff(y, 1);
s = 0:ds:distance(end);
refer_path= interp1(distance, points, distance_specific, 'spline');
figure(1)
% 绘制拟合曲线
plot(refer_path(:, 1), refer_path(:, 2),'b-',x, y,'r.');
hold on
refer_path_x = refer_path(:,1); % x
refer_path_y = refer_path(:,2); % y
for i=1:length(refer_path)if i==1dx = refer_path(i + 1, 1) - refer_path(i, 1);dy = refer_path(i + 1, 2) - refer_path(i, 2);ddx = refer_path(3, 1) + refer_path(1, 1) - 2 * refer_path(2, 1);ddy = refer_path(3, 2) + refer_path(1, 2) - 2 * refer_path(2, 2);elseif i==length(refer_path)dx = refer_path(i, 1) - refer_path(i - 1, 1);dy = refer_path(i, 2) - refer_path(i - 1, 2);ddx = refer_path(i, 1) + refer_path(i - 2, 1) - 2 * refer_path(i - 1, 1);ddy = refer_path(i, 2) + refer_path(i - 2, 2) - 2 * refer_path(i - 1, 2);elsedx = refer_path(i + 1, 1) - refer_path(i, 1);dy = refer_path(i + 1, 2) - refer_path(i, 2);ddx = refer_path(i + 1, 1) + refer_path(i - 1, 1) - 2 * refer_path(i, 1);ddy = refer_path(i + 1, 2) + refer_path(i - 1, 2) - 2 * refer_path(i, 2);endrefer_path(i,3)=atan2(dy, dx);%yawrefer_path(i,4)=(ddy * dx - ddx * dy) / ((dx ^ 2 + dy ^ 2) ^ (3 / 2));
end
figure(2)
plot(refer_path(:, 3),'b-');
figure(3)
plot(refer_path(:, 4),'b-')
%
%%目标及初始状态
L=2;%车辆轴距
v=2;%初始速度
dt=0.05;%时间间隔
goal=refer_path(end,1:2);
x_0=refer_path_x(1);
y_0=refer_path_y(1);
psi_0 = refer_path(1, 3);
% %运动学模型
ugv = KinematicModel(x_0, y_0, psi_0, v, dt, L);
Q = eye(3) * 3.0;
R = eye(2) * 2.0;
robot_state = zeros(4, 1);
step_points = length(refer_path(:, 1));
for i=1:1:step_pointsrobot_state(1)=ugv.x;robot_state(2)=ugv.y;robot_state(3)=ugv.psi;robot_state(4)=ugv.v;[e, k, ref_yaw, min_idx] = calc_track_error(robot_state(1), robot_state(2), refer_path);ref_delta = atan2(L * k, 1);[A, B] = state_space( robot_state(4), ref_delta, ref_yaw, dt, L);delta = lqr(robot_state, refer_path, min_idx, A, B, Q, R);delta = delta + ref_delta;[ugv.x, ugv.y, ugv.psi, ugv.v] = update(0, delta, dt, L, robot_state(1), robot_state(2),robot_state(3), robot_state(4));ugv.record_x(end + 1 ) = ugv.x;ugv.record_y(end + 1 ) = ugv.y;ugv.record_psi(end + 1 ) = ugv.psi;ugv.record_phy(end + 1 ) = ref_delta;
end
figure(4)
% 绘制拟合曲线
% scr_size = get(0,'screensize');
% set(gcf,'outerposition', [1 1 scr_size(4) scr_size(4)]);
plot(ugv.record_x , ugv.record_y, Color='m',LineStyle='--',LineWidth=2);
axis([-40,40,-40,40])
grid on
hold on
% 绘制车辆曲线
axis equal
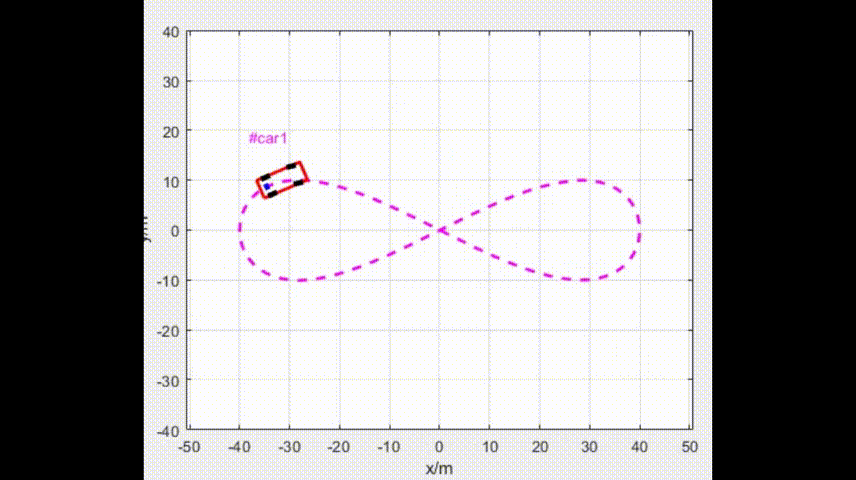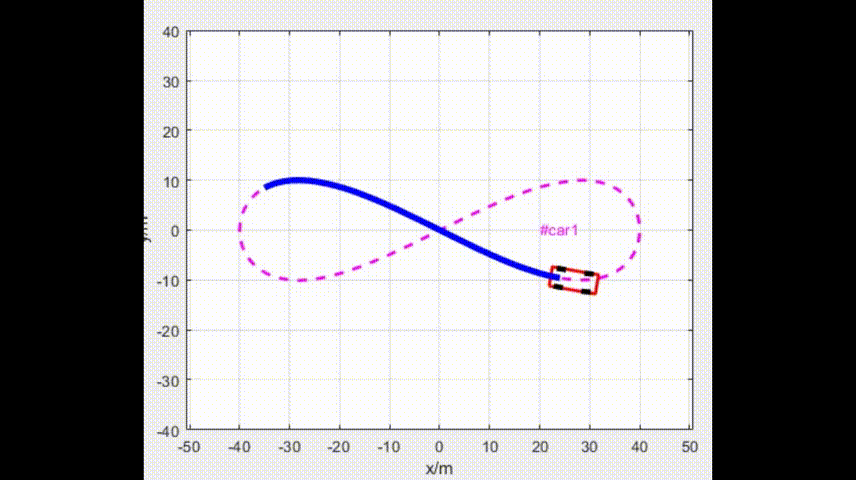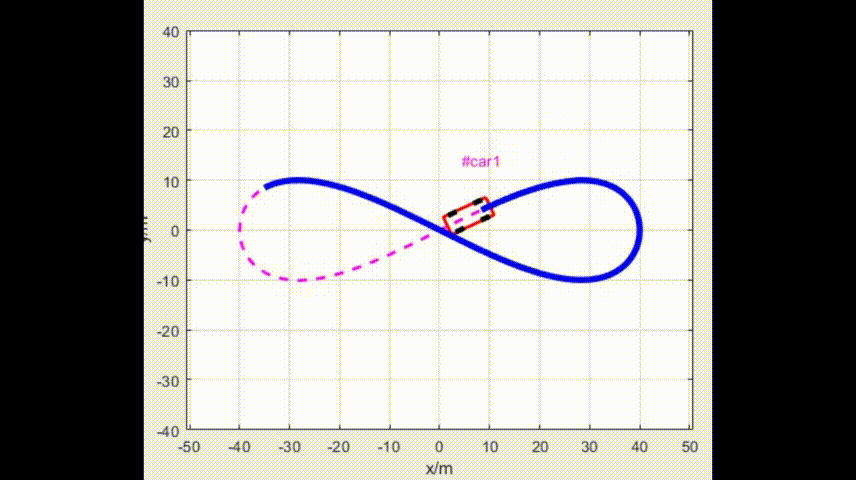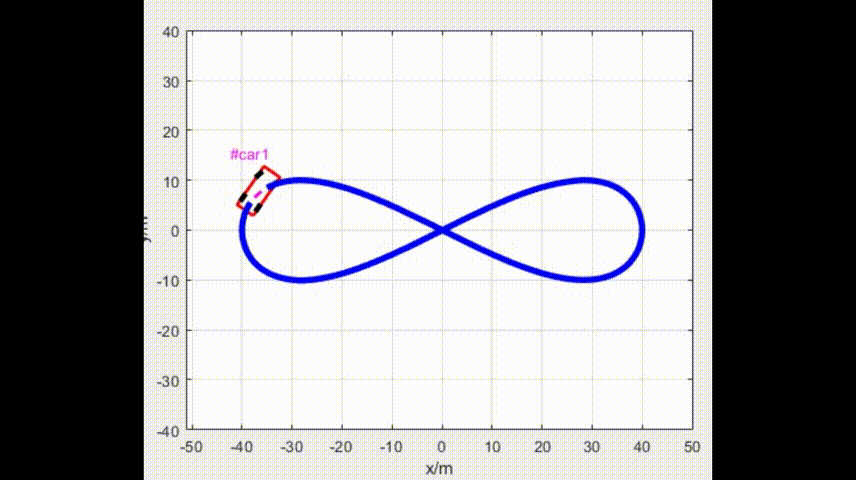
for ii = 1:1:length(ugv.record_x)h = PlotCarbox(ugv.record_x(ii), ugv.record_y(ii), ugv.record_psi(ii), 'Color', 'r',LineWidth=2);h1 = plot(ugv.record_x(1:ii), ugv.record_y(1:ii),'Color', 'b');th1 = text(ugv.record_x(ii), ugv.record_y(ii)+10, ['#car', num2str(1)], 'Color', 'm');set(th1, {'HorizontalAlignment'},{'center'});h2 = PlotCarWheels(ugv.record_x(ii), ugv.record_y(ii), ugv.record_psi(ii),ugv.record_phy(ii),'k',LineWidth=2);h3 = plot(ugv.record_x(1:ii) , ugv.record_y(1:ii), Color='b',LineStyle='-',LineWidth=4);drawnowdelete(h); delete(h1);delete(th1);delete(h3);for jj = 1:1:size(h2)delete(h2{jj});end
end
%
function [P] = cal_Ricatti(A, B, Q, R)Qf = Q;P = Qf;iter_max = 100;Eps = 1e-4;for step = 1:1:iter_maxP_bar = Q + A' * P * A - A' * P * B * pinv(R + B' * P *B) * B' * P * A;criteria = max(abs(P_bar - P));if criteria < Epsbreak;endP = P_bar;endend
%%LQR控制器
function[u_star]=lqr(robot_state, refer_path, s0, A, B, Q, R)x = robot_state(1:3) - refer_path(s0,1:3)';P = cal_Ricatti(A, B, Q, R);K= -pinv(R + B' * P * B) * B' * P * A;u = K * x;%状态反馈u_star = u(2);
endfunction [e, k, yaw, min_idx]=calc_track_error(x, y, refer_path)p_num = length(refer_path);d_x = zeros(p_num, 1);d_y = zeros(p_num, 1);d = zeros(p_num, 1);for i=1:1:p_num d_x(i) = refer_path(i, 1) - x; d_y(i) = refer_path(i, 2) - y;endfor i=1:1:p_num d(i) = sqrt(d_x(i) ^2 + d_y(i) ^ 2) ;end[~, min_idx] = min(d); yaw = refer_path(min_idx, 3);k = refer_path(min_idx, 4);angle= normalize_angle(yaw - atan2(d_y(min_idx), d_x(min_idx)));e = d(min_idx);if angle < 0e = e*(-1);end
end
%%将角度取值范围限定为[-pi,pi]
function [angle]=normalize_angle(angle)while angle > piangle = angle - 2*pi;endwhile angle < piangle = angle + 2*pi;end
end
function [x_next, y_next, psi_next, v_next] = update(a, delta_f, dt, L, x, y, psi, v)x_next = x + v * cos(psi) * dt;y_next = y + v * sin(psi) * dt;psi_next = psi + v / L * tan(delta_f) * dt;v_next = v + a * dt;
end
function [A, B]=state_space(v, ref_delta, ref_yaw, dt, L)A=[ 1.0, 0.0, -v * dt * sin(ref_yaw);0.0, 1.0, v * dt * cos(ref_yaw);0.0, 0.0, 1.0 ];B =[ dt * cos(ref_yaw), 0;dt * sin(ref_yaw), 0;dt * tan(ref_delta) / L, v * dt / (L * cos(ref_delta) * cos(ref_delta))];
end
function h = PlotCarbox(x, y, theta, varargin)
Params = GetVehicleParams();carbox = [-Params.Lr -Params.Lb/2; Params.Lw+Params.Lf -Params.Lb/2; Params.Lw+Params.Lf Params.Lb/2; -Params.Lr Params.Lb/2];
carbox = [carbox; carbox(1, :)];transformed_carbox = [carbox ones(5, 1)] * GetTransformMatrix(x, y, theta)';
h = plot(transformed_carbox(:, 1), transformed_carbox(:, 2), varargin{:});end
function hs = PlotCarWheels(x, y, theta, phy, varargin)
Params = GetVehicleParams();wheel_box = [-Params.wheel_radius -Params.wheel_width / 2;+Params.wheel_radius -Params.wheel_width / 2;+Params.wheel_radius +Params.wheel_width / 2;-Params.wheel_radius +Params.wheel_width / 2];front_x = x + Params.Lw * cos(theta);
front_y = y + Params.Lw * sin(theta);
track_width_2 = (Params.Lb - Params.wheel_width / 2) / 2;boxes = {TransformBox(wheel_box, x - track_width_2 * sin(theta), y + track_width_2 * cos(theta), theta);TransformBox(wheel_box, x + track_width_2 * sin(theta), y - track_width_2 * cos(theta), theta);TransformBox(wheel_box, front_x - track_width_2 * sin(theta), front_y + track_width_2 * cos(theta), theta+phy);TransformBox(wheel_box, front_x + track_width_2 * sin(theta), front_y - track_width_2 * cos(theta), theta+phy);
};hs = cell(4, 1);
for ii = 1:4hs{ii} = fill(boxes{ii}(:, 1), boxes{ii}(:, 2), varargin{:});
endendfunction transformed = TransformBox(box, x, y, theta)
transformed = [box; box(1, :)];
transformed = [transformed ones(5, 1)] * GetTransformMatrix(x, y, theta)';
transformed = transformed(:, 1:2);
end
function mat = GetTransformMatrix(x, y, theta)
mat = [ ...cos(theta) -sin(theta), x; ...sin(theta) cos(theta), y; ...0 0 1];
end3.2 运动学结构体:
classdef KinematicModel<handlepropertiesx;y;psi;v;dt;L;record_x;record_y;record_psi;record_phy;endmethodsfunction self=KinematicModel(x, y, psi, v, dt, L)self.x=x;self.y=y;self.psi=psi;self.v = v;self.L = L;% 实现是离散的模型self.dt = dt;self.record_x = [];self.record_y= [];self.record_psi= [];self.record_phy= [];end
end
end四、仿真参数和效果
4.1 参数配置
%期望轨迹
y0 = @(t_step) 10*sin(2 * t_step + 1);
x0_dot= @(t_step) 5 * 2 * cos(2 * t_step + 1);
L=2;%车辆轴距
v=2;%初始速度
dt=0.05;%时间间隔
Q = eye(3) * 3.0;
R = eye(2) * 2.0;
robot_state = zeros(4, 1);
VehicleParams.Lw = 2.8 * 2; % wheel base
VehicleParams.Lf = 0.96 * 2; % front hang
VehicleParams.Lr = 0.929 * 2; % rear hang
VehicleParams.Lb = 1.942 * 2; % width
VehicleParams.Ll = VehicleParams.Lw + VehicleParams.Lf + VehicleParams.Lr; % length
VehicleParams.f2x = 1/4 * (3*VehicleParams.Lw + 3*VehicleParams.Lf - VehicleParams.Lr);
VehicleParams.r2x = 1/4 * (VehicleParams.Lw + VehicleParams.Lf - 3*VehicleParams.Lr);
VehicleParams.radius = 1/2 * sqrt((VehicleParams.Lw + VehicleParams.Lf + VehicleParams.Lr) ^ 2 / 4 + VehicleParams.Lb ^ 2);
VehicleParams.a_max = 0.5;
VehicleParams.v_max = 2.5;
VehicleParams.phi_max = 0.7;
VehicleParams.omega_max = 0.5;
% for wheel visualization
VehicleParams.wheel_radius = 0.32*2;
VehicleParams.wheel_width = 0.22*2;
iter_max = 100;
Eps = 1e-4;4.1 仿真效果

相关文章:

面向阿克曼移动机器人(自行车模型)的LQR(最优二次型调节器)路径跟踪方法
线性二次调节器(Linear Quadratic Regulator,LQR)是针对线性系统的最优控制方法。LQR 方法标准的求解体系是在考虑到损耗尽可能小的情况下, 以尽量小的代价平衡其他状态分量。一般情况下,线性系统在LQR 控制方法中用状态空间方程描…...

【运维】在 Docker 容器中指定 UTF-8 编码:方法与技巧
在 Docker 容器中指定 UTF-8 编码:方法与技巧 在日常开发中,我们常常需要确保应用程序能正确处理各种字符编码,尤其是 UTF-8 编码。在 Docker 容器中运行应用程序时,正确设置字符编码尤为重要,因为容器通常是跨平台、…...

primetime中cell和net的OCV
文章目录 前言一、Cell OCV1. POCV coefficient file2. POCV Slew-Load Table in Liberty Variation Format(LVF lib) 二、Net OCV三、如何check OCV是否已加上?总结 前言 在生产中,外界环境的各种变化,比如PVT&#…...
FlinkX学习
FlinkX学习 FlinkX安装 由于flinkx已经改名chunjun 官网已不存在 (https://gitee.com/lugela/flinkx#flinkx)这里可以看到flinkx的操作文档 1、上传并解压 unzip flinkx-1.10.zip -d /usr/local/soft/2、配置环境变量 FLINKX_HOME/usr/local/soft/flinkx-1.10 export PATH$F…...

新书速览|解密AI绘画与修图: Stable Diffusion+Photoshop
《解密AI绘画与修图: Stable DiffusionPhotoshop》 本书内容 《解密AI绘画与修图:Stable DiffusionPhotoshop》全面介绍了Photoshop和Stable Diffusion的交互方式,以及各自的AI功能和具体使用方法。除了讲解功能,还通过实际案例加…...

1111111111111
计算机视觉技术在医疗领域的应用正迅速成为推动医疗进步的关键力量。通过高级图像处理和分析,这项技术在医学影像分析(包括CT、MRI和X光图像)、实时手术辅助、患者监测和护理、以及疾病早期诊断等方面展现出巨大的潜力。然而,随着…...

云原生概念
云原生是一种新型的技术体系和方法论,旨在充分利用云计算环境的优势,使应用程序更具有弹性、可伸缩性、可靠性和效率。以下是云原生的详细解释: 定义: 云原生是一种基于分布部署和统一运管的分布式云,以容器、微服务、…...

NoSQL之Redis高可用与优化
一、Redis高可用 在web服务器中,高可用是指服务器可以正常访问的时间,衡量的标准是在多长时间内可以提供正常服务(99.9%、99.99%、99.999%等等)。 但是在Redis语境中,高可用的含义似乎要宽泛一些,除了保证…...

MySQL 常见存储引擎详解(一)
本篇主要介绍MySQL中常见的存储引擎。 目录 一、InnoDB引擎 简介 特性 最佳实践 创建InnoDB 存储文件 二、MyISAM存储引擎 简介 特性 创建MyISAM表 存储文件 存储格式 静态格式 动态格式 压缩格式 三、MEMORY存储引擎 简介 特点 创建MEMORY表 存储文件 内…...

Leetcode 股票买卖
买卖股票最佳时机 I II 不限制交易次数 prices [7,1,5,3,6,4] 启发思路:最后一天发生了什么? 从第0天到第5天结束时的利润 从第0天到第4天结束时的利润 第5天的利润 (第5天的利润:0/-4/4) 关键词:天…...
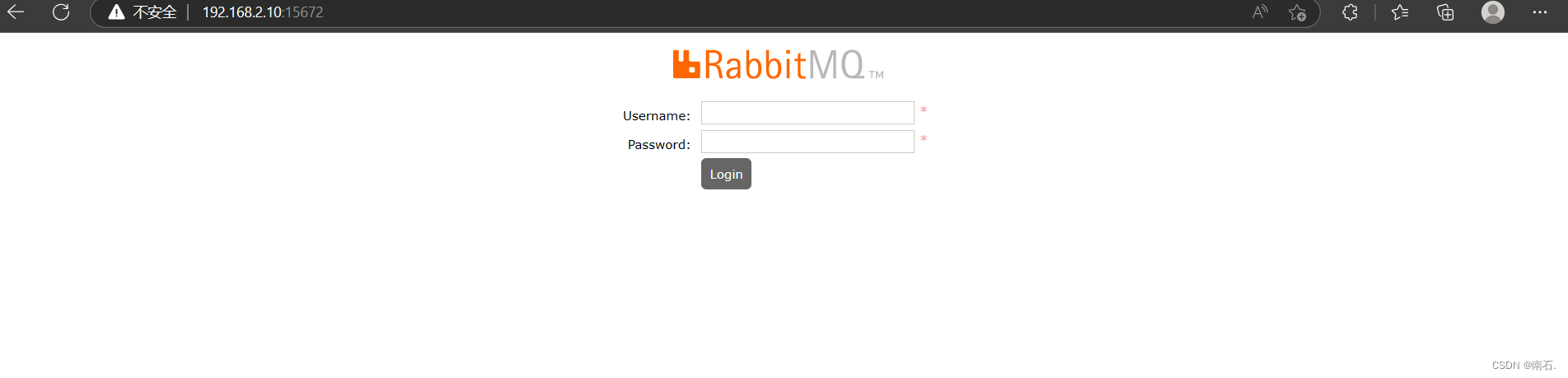
小白学习手册:轻松理解MQ消息队列
目录 # 开篇 RabbitMQ介绍 通讯概念 1. 初始MQ及类型 2. MQ的架构 2.1 RabbitMQ的结构和概念 2.2 RabbitMQ消息流示意图 3. MQ下载使用 3.1 Docker下载MQ参考 3.2 进入RabbitMQ # 开篇 MessagesQueue 是一个抽象概念,用于描述消息队列系统的一般特性和功能…...

electron线上更新
一、安装electron-updater npm install --save electron-updater二、在main.js中引入使用 import { autoUpdater } from electron; if (!isDev) {const serverUrl https://your-update-server.com; // 自定义更新服务器地址或GitHub Releases地址autoUpdater.setFeedURL(${…...

谈谈检测浏览器类型
前几天被问到如何检测浏览器类型,我突然发现我对此并不了解,之前的项目中也没有使用到过,只隐约记得通过一个自带的方法即可获取。所以今天特意来仔细补习一下。 核心:navigator.userAgent 1.正则表达式 2.引用外部库 3.判断浏…...

Django 和 Django REST framework 创建对外 API
1. 环境准备 确保你已经安装了 Python 和 Django。如果尚未安装 Django REST framework,通过 pip 安装它: pip install djangorestframework 2. 创建 Django 项目 如果你还没有 Django 项目,可以通过以下命令创建: django-ad…...
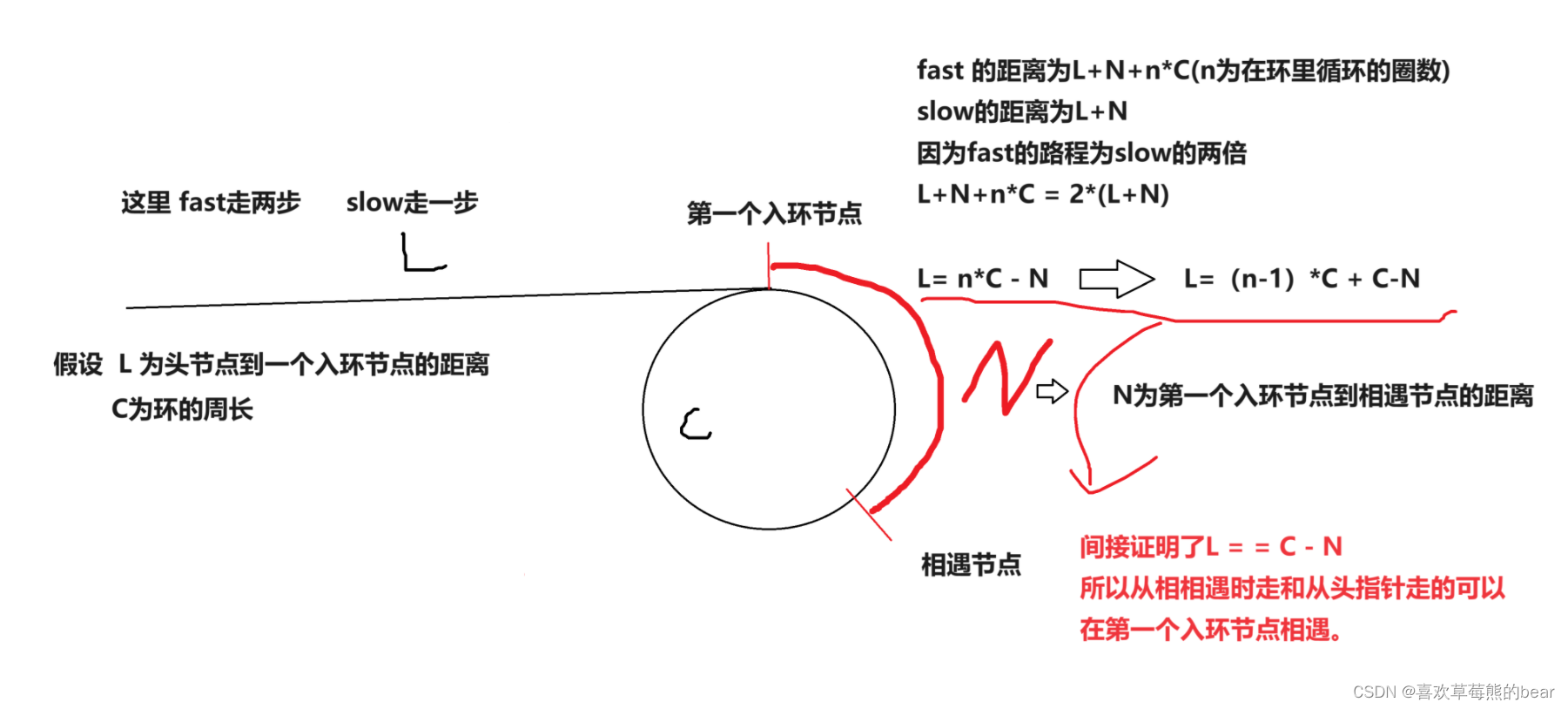
数据结构之“刷链表题”
🌹个人主页🌹:喜欢草莓熊的bear 🌹专栏🌹:数据结构 目录 前言 一、相交链表 题目链接 大致思路 代码实现 二、环形链表1 题目链接 大致思路 代码实现 三、环形链表2 题目链接 大致思路 代码实…...
复分析——第9章——椭圆函数导论(E.M. Stein R. Shakarchi)
第 9 章 椭圆函数导论 (An Introduction to Elliptic Functions) The form that Jacobi had given to the theory of elliptic functions was far from perfection; its flaws are obvious. At the base we find three fundamental functions sn, cn and dn. These functio…...

使用kubeadm安装k8s并部署应用
安装k8s 1. 准备机器 准备三台机器 192.168.136.104 master节点 192.168.136.105 worker节点 192.168.136.106 worker节点2. 安装前配置 1.基础环境 ######################################################################### #关闭防火墙: 如果是云服务器&…...
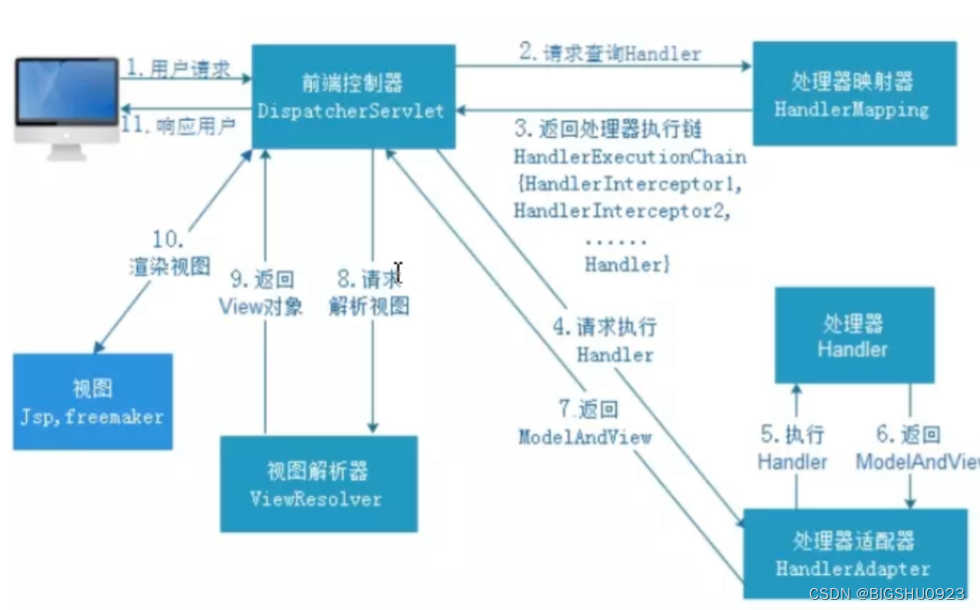
springMVC学习
概述 Spring MVC(Model-View-Controller,模型-视图-控制器)是Spring框架的一部分,用于构建基于Java的Web应用程序。它遵循MVC设计模式,分离了应用程序的不同方面(输入逻辑、业务逻辑和UI逻辑)&…...

深入探讨光刻技术:半导体制造的关键工艺
前言 光刻(Photolithography)是现代半导体制造过程中不可或缺的一环,它的精度和能力直接决定了芯片的性能和密度。本文将详细介绍光刻技术的基本原理、过程、关键技术及其在半导体制造中的重要性。 光刻技术的基本原理 光刻是一种利用光化…...
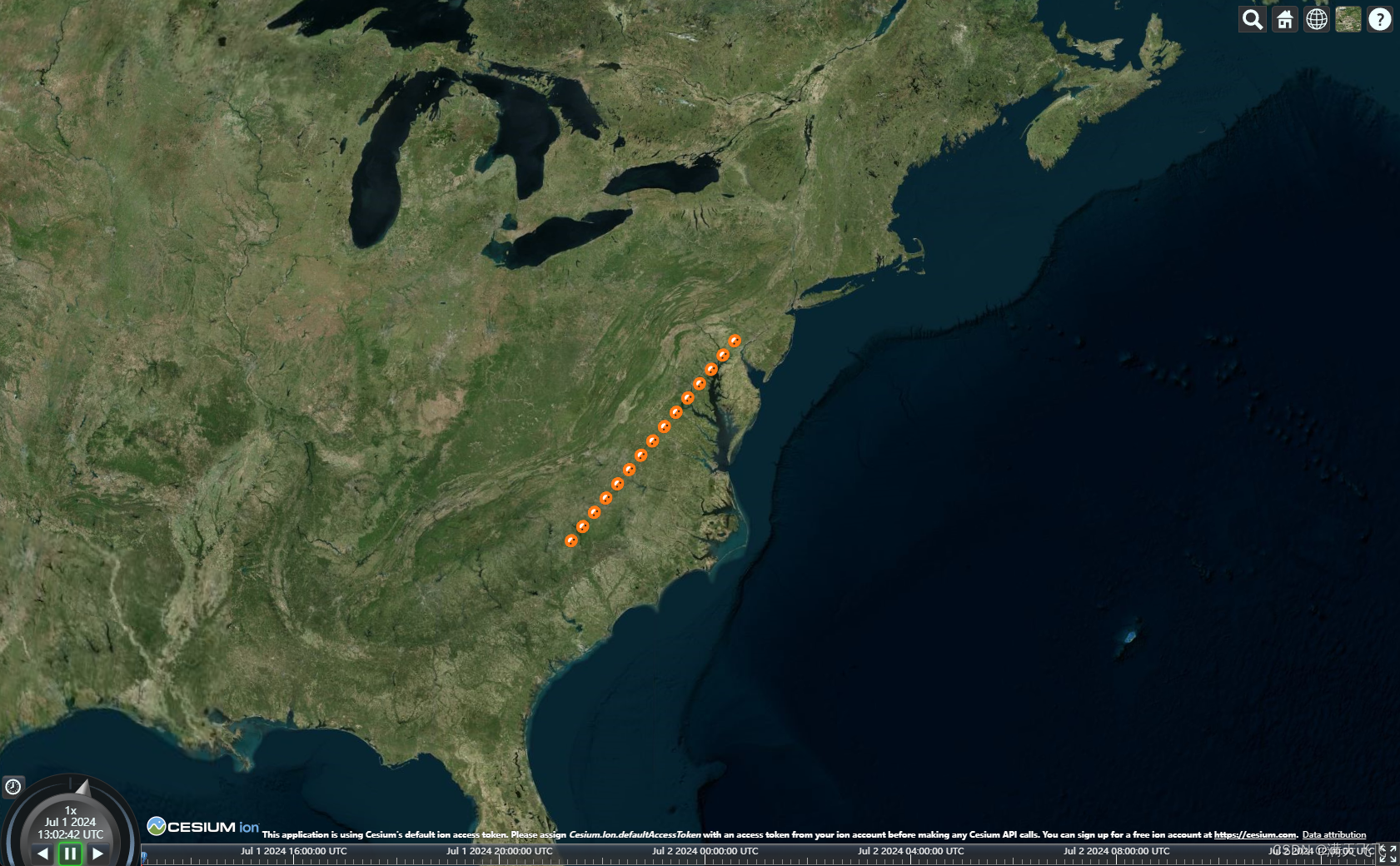
CesiumJS【Basic】- #042 绘制纹理线(Primitive方式)
文章目录 绘制纹理线(Primitive方式)1 目标2 代码2.1 main.ts3 资源文件绘制纹理线(Primitive方式) 1 目标 使用Primitive方式绘制纹理线 2 代码 2.1 main.ts var start = Cesium.Cartesian3.fromDegrees(-75.59777, 40.03883);var...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

虚幻基础:角色旋转
能帮到你的话,就给个赞吧 😘 文章目录 移动组件使用控制器所需旋转:组件 使用 控制器旋转将旋转朝向运动:组件 使用 移动方向旋转 控制器旋转和移动旋转 缺点移动旋转:必须移动才能旋转,不移动不旋转控制器…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...

Springboot 高校报修与互助平台小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,高校报修与互助平台小程序被用户普遍使用,为…...

AI书签管理工具开发全记录(十八):书签导入导出
文章目录 AI书签管理工具开发全记录(十八):书签导入导出1.前言 📝2.书签结构分析 📖3.书签示例 📑4.书签文件结构定义描述 🔣4.1. 整体文档结构4.2. 核心元素类型4.3. 层级关系4.…...
