vant ( weapp ) - - - - - van-tabs组件选中下划线初始位置异常
这里写自定义目录标题
- 1. 当前效果展示
- 2. 官方解释 & 方案
1. 当前效果展示
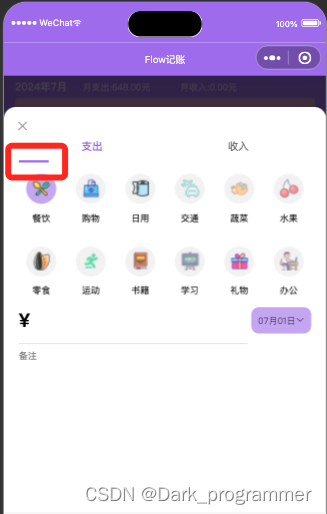
明显可以看到框内的光标位置偏移了,但当切换一次之后就会显示正常。
只有初次打开的时候,才会出现上述问题。
代码如下:
<van-popup show="{{ makeShow }}" ><van-tabs active="{{ active }}" animated title-active-color='#9c6af1' bind:click="onChange"><van-tab wx:for="{{maps}}" wx:for-item="tabItem" title="{{tabItem.title}}" wx:key="index">// 这里是内容{{item.content}}</van-tab></van-tabs>
</van-popup>
2. 官方解释 & 方案
👇下面是官方给出的解释以及方案
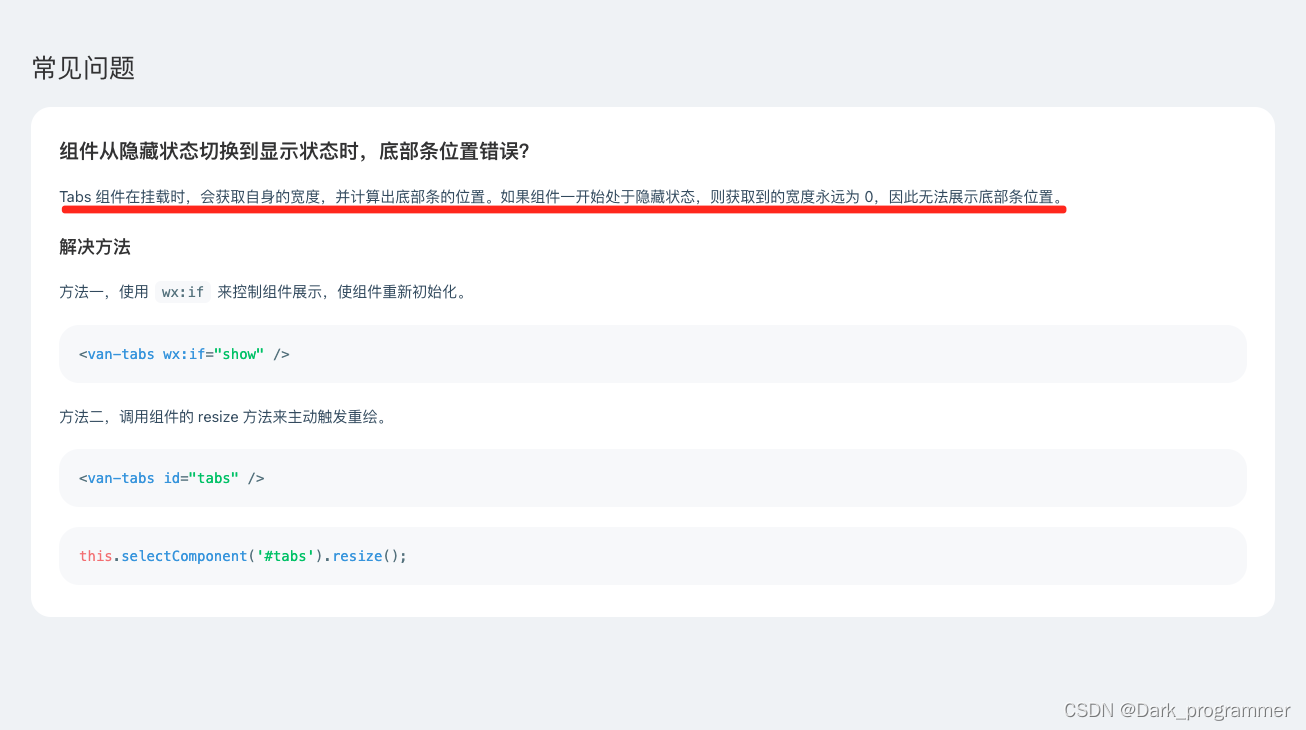
由于我的van-tabs是在弹窗里展示的,使用方法二进行resize方案不适合我。
所以采用方案一,逻辑如下
切换弹窗展示状态之后,在回调函数里再修改其状态即可
需要给van-tabs增加wx:if属性
修改如下:
<van-popup show="{{ makeShow }}" ><van-tabs wx:if="{{ isTabsReady }}" active="{{ active }}" animated title-active-color='#9c6af1' bind:click="onChange"><van-tab wx:for="{{maps}}" wx:for-item="tabItem" title="{{tabItem.title}}" wx:key="index">// 这里是内容{{item.content}}</van-tab></van-tabs>
</van-popup>
this.setData({makeShow: true, // 修改popup展示状态
},()=>{this.setData({isTabsReady: true // 修改tabs展示状态})
})
如此初始展示就正常了

相关文章:

vant ( weapp ) - - - - - van-tabs组件选中下划线初始位置异常
这里写自定义目录标题 1. 当前效果展示2. 官方解释 & 方案 1. 当前效果展示 明显可以看到框内的光标位置偏移了,但当切换一次之后就会显示正常。 只有初次打开的时候,才会出现上述问题。 代码如下: <van-popup show"{{ makeSho…...
)
007 栈(lua)
文章目录 Lua本身支持动态数组,通过表(table)实现,它类似于Java中的ArrayList。Lua的表是灵活的数组和字典的混合体。对于栈的实现,我们可以简单地使用一个表来模拟。 这里是一个简单的Lua栈实现,它包含了p…...

SQL中Order by详解
在 MySQL 中,ORDER BY 语句用于对查询结果进行排序。 语法: SELECT column1, column2,... FROM table_name ORDER BY column_name [ASC | DESC];以下是对其主要部分的详细解释: column_name :指定要依据其进行排序的列名。 ASC…...

【git】存在git LFS文件时如何处理
目录 1. 安装 Git LFS2. 初始化 Git LFS3. 跟踪大文件4. 添加和提交文件5. 克隆和拉取包含 LFS 文件的仓库 1. 安装 Git LFS 首先,你需要在你的系统上安装 Git LFS。你可以使用以下命令来安装: 在 Linux 上 # 对于基于 Debian 的系统 (如 Ubuntu) sud…...
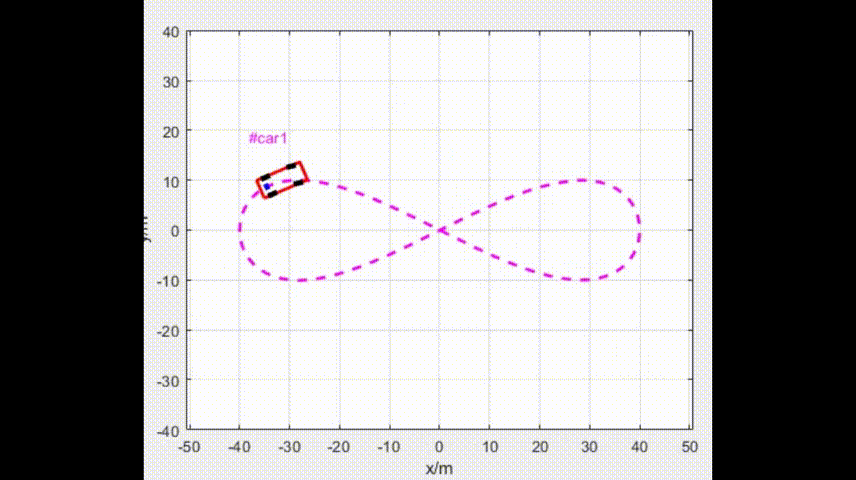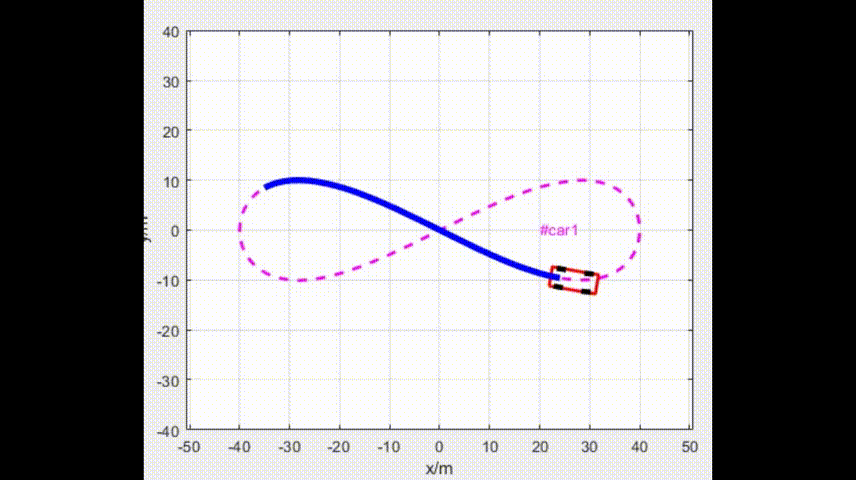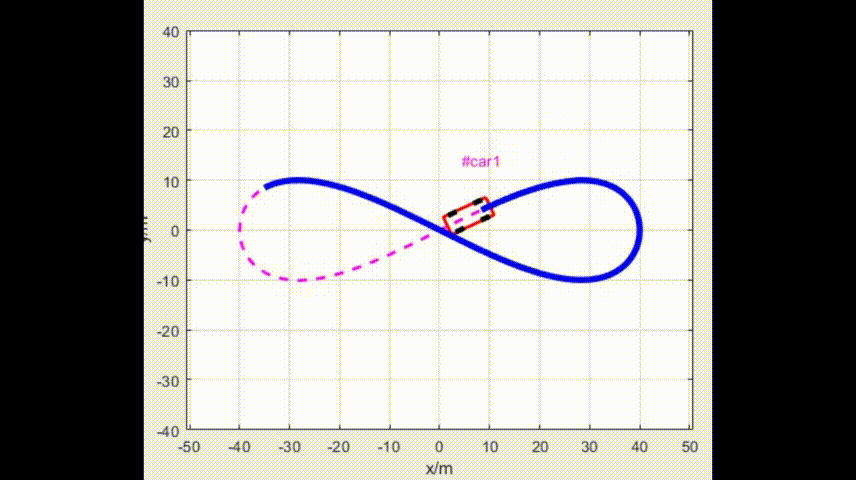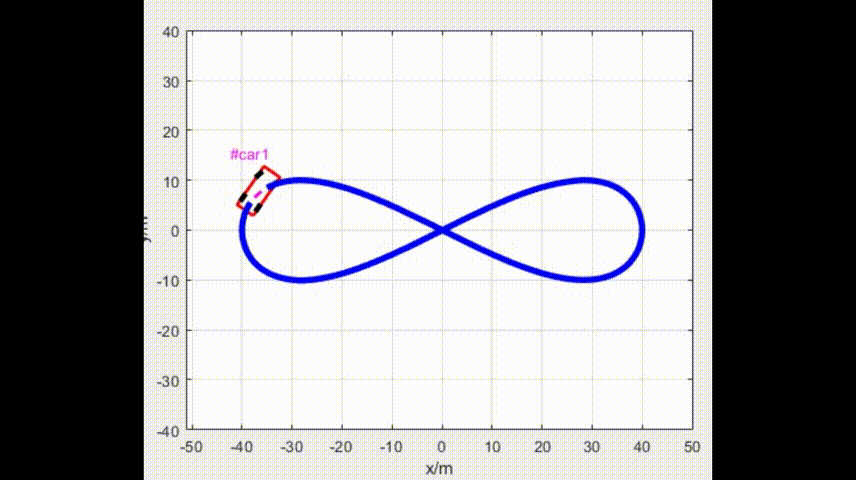
面向阿克曼移动机器人(自行车模型)的LQR(最优二次型调节器)路径跟踪方法
线性二次调节器(Linear Quadratic Regulator,LQR)是针对线性系统的最优控制方法。LQR 方法标准的求解体系是在考虑到损耗尽可能小的情况下, 以尽量小的代价平衡其他状态分量。一般情况下,线性系统在LQR 控制方法中用状态空间方程描…...

【运维】在 Docker 容器中指定 UTF-8 编码:方法与技巧
在 Docker 容器中指定 UTF-8 编码:方法与技巧 在日常开发中,我们常常需要确保应用程序能正确处理各种字符编码,尤其是 UTF-8 编码。在 Docker 容器中运行应用程序时,正确设置字符编码尤为重要,因为容器通常是跨平台、…...

primetime中cell和net的OCV
文章目录 前言一、Cell OCV1. POCV coefficient file2. POCV Slew-Load Table in Liberty Variation Format(LVF lib) 二、Net OCV三、如何check OCV是否已加上?总结 前言 在生产中,外界环境的各种变化,比如PVT&#…...
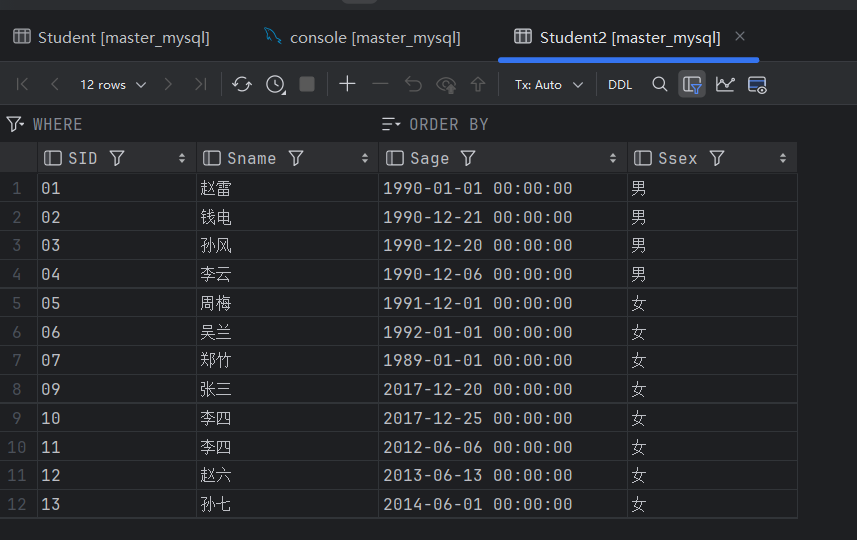
FlinkX学习
FlinkX学习 FlinkX安装 由于flinkx已经改名chunjun 官网已不存在 (https://gitee.com/lugela/flinkx#flinkx)这里可以看到flinkx的操作文档 1、上传并解压 unzip flinkx-1.10.zip -d /usr/local/soft/2、配置环境变量 FLINKX_HOME/usr/local/soft/flinkx-1.10 export PATH$F…...

新书速览|解密AI绘画与修图: Stable Diffusion+Photoshop
《解密AI绘画与修图: Stable DiffusionPhotoshop》 本书内容 《解密AI绘画与修图:Stable DiffusionPhotoshop》全面介绍了Photoshop和Stable Diffusion的交互方式,以及各自的AI功能和具体使用方法。除了讲解功能,还通过实际案例加…...

1111111111111
计算机视觉技术在医疗领域的应用正迅速成为推动医疗进步的关键力量。通过高级图像处理和分析,这项技术在医学影像分析(包括CT、MRI和X光图像)、实时手术辅助、患者监测和护理、以及疾病早期诊断等方面展现出巨大的潜力。然而,随着…...

云原生概念
云原生是一种新型的技术体系和方法论,旨在充分利用云计算环境的优势,使应用程序更具有弹性、可伸缩性、可靠性和效率。以下是云原生的详细解释: 定义: 云原生是一种基于分布部署和统一运管的分布式云,以容器、微服务、…...

NoSQL之Redis高可用与优化
一、Redis高可用 在web服务器中,高可用是指服务器可以正常访问的时间,衡量的标准是在多长时间内可以提供正常服务(99.9%、99.99%、99.999%等等)。 但是在Redis语境中,高可用的含义似乎要宽泛一些,除了保证…...

MySQL 常见存储引擎详解(一)
本篇主要介绍MySQL中常见的存储引擎。 目录 一、InnoDB引擎 简介 特性 最佳实践 创建InnoDB 存储文件 二、MyISAM存储引擎 简介 特性 创建MyISAM表 存储文件 存储格式 静态格式 动态格式 压缩格式 三、MEMORY存储引擎 简介 特点 创建MEMORY表 存储文件 内…...

Leetcode 股票买卖
买卖股票最佳时机 I II 不限制交易次数 prices [7,1,5,3,6,4] 启发思路:最后一天发生了什么? 从第0天到第5天结束时的利润 从第0天到第4天结束时的利润 第5天的利润 (第5天的利润:0/-4/4) 关键词:天…...
小白学习手册:轻松理解MQ消息队列
目录 # 开篇 RabbitMQ介绍 通讯概念 1. 初始MQ及类型 2. MQ的架构 2.1 RabbitMQ的结构和概念 2.2 RabbitMQ消息流示意图 3. MQ下载使用 3.1 Docker下载MQ参考 3.2 进入RabbitMQ # 开篇 MessagesQueue 是一个抽象概念,用于描述消息队列系统的一般特性和功能…...

electron线上更新
一、安装electron-updater npm install --save electron-updater二、在main.js中引入使用 import { autoUpdater } from electron; if (!isDev) {const serverUrl https://your-update-server.com; // 自定义更新服务器地址或GitHub Releases地址autoUpdater.setFeedURL(${…...

谈谈检测浏览器类型
前几天被问到如何检测浏览器类型,我突然发现我对此并不了解,之前的项目中也没有使用到过,只隐约记得通过一个自带的方法即可获取。所以今天特意来仔细补习一下。 核心:navigator.userAgent 1.正则表达式 2.引用外部库 3.判断浏…...

Django 和 Django REST framework 创建对外 API
1. 环境准备 确保你已经安装了 Python 和 Django。如果尚未安装 Django REST framework,通过 pip 安装它: pip install djangorestframework 2. 创建 Django 项目 如果你还没有 Django 项目,可以通过以下命令创建: django-ad…...
数据结构之“刷链表题”
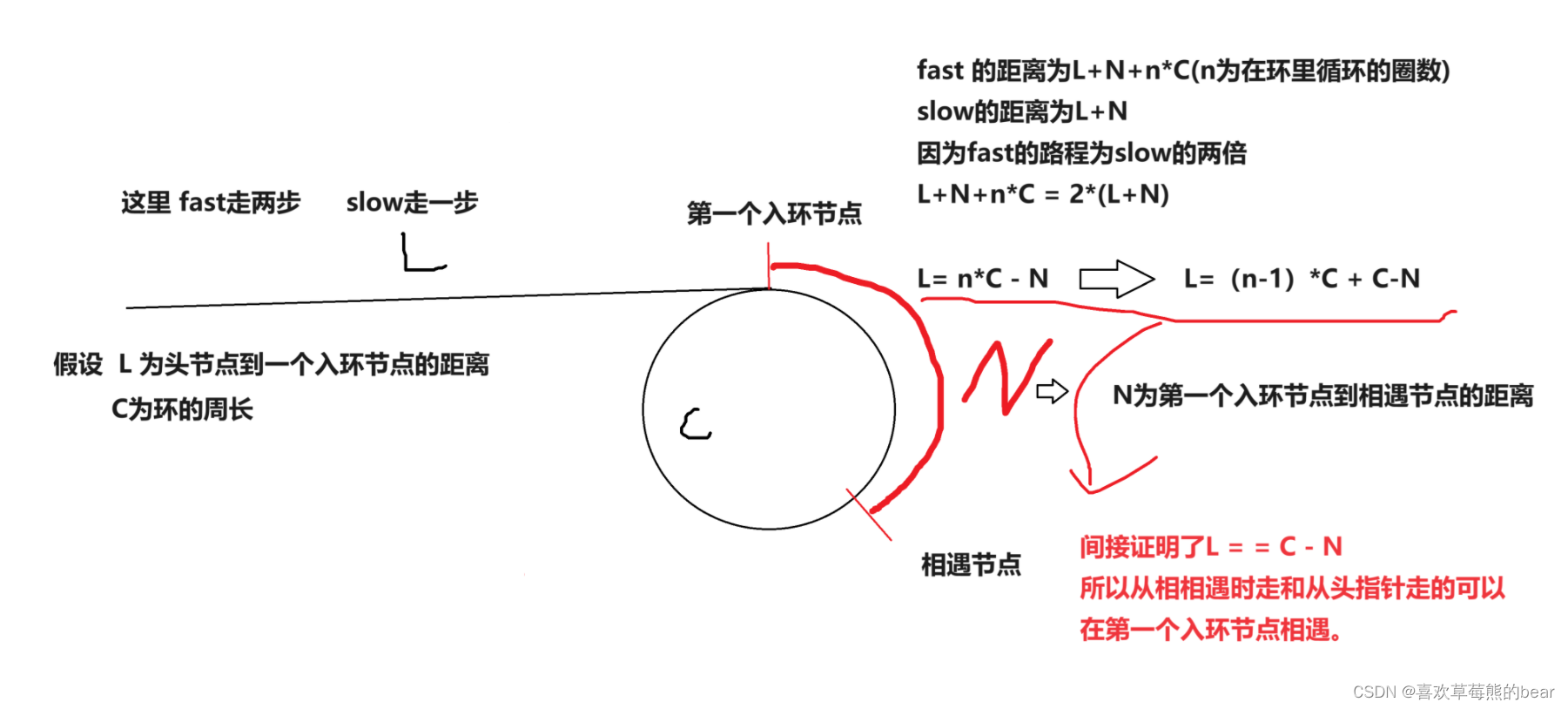
🌹个人主页🌹:喜欢草莓熊的bear 🌹专栏🌹:数据结构 目录 前言 一、相交链表 题目链接 大致思路 代码实现 二、环形链表1 题目链接 大致思路 代码实现 三、环形链表2 题目链接 大致思路 代码实…...
复分析——第9章——椭圆函数导论(E.M. Stein R. Shakarchi)
第 9 章 椭圆函数导论 (An Introduction to Elliptic Functions) The form that Jacobi had given to the theory of elliptic functions was far from perfection; its flaws are obvious. At the base we find three fundamental functions sn, cn and dn. These functio…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...

Tauri2学习笔记
教程地址:https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引:https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多,我按照Tauri1的教程来学习&…...
