大模型压缩:基于贝叶斯优化的自适应低秩分解
1.方法
1.1 基于特征的高维空间低秩分解
PCA已经是老朋友了,每次一说主成分都会出现PCA。这篇文章1利用预训练数据的子集作为校准数据集 D c a l = { x i } i = 1 n \mathcal{D}_{cal}=\{x_{i}\}_{i=1}^{n} Dcal={xi}i=1n,首先用校准数据集的样本协方差矩阵(SCM)估计整个特征空间分布的Y的协方差矩阵
C o v S ( Y ) = 1 n − 1 ∑ i = 1 n ( y i − y ˉ ) T ( y i − y ˉ ) (1) Cov_S(\boldsymbol{Y})=\frac{1}{n-1}\sum_{i=1}^n(\boldsymbol{y}_i-\bar{\boldsymbol{y}})^T(\boldsymbol{y}_i-\bar{\boldsymbol{y}})\tag{1} CovS(Y)=n−11i=1∑n(yi−yˉ)T(yi−yˉ)(1)
式中 y i \boldsymbol{y}_i yi表示 x i \boldsymbol{x}_i xi的特征, y ˉ \bar{\boldsymbol{y}} yˉ是校准数据集的特征值平均值。但文章指出,计算高维的协方差矩阵并不简单,他们提出了合并协方差矩阵(PCM),把校准数据集分成 m m m组,对每一组分别计算协方差矩阵最后求平均得PCM
C o v P ( Y ) = 1 m ∑ k = 1 m C o v S ( Y k ) (2) Cov_P(\boldsymbol{Y})=\frac{1}{m}\sum_{k=1}^mCov_S(\boldsymbol{Y}_k)\tag{2} CovP(Y)=m1k=1∑mCovS(Yk)(2)
1.2 基于贝叶斯优化得低秩分配
对于每一层,甚至每一层的不同矩阵对低秩分解得敏感度不同,对于一个模型 f ( ⋅ ; θ ) f(\cdot;\theta) f(⋅;θ),引入一组压缩率 λ = { λ i } i = 1 k \lambda=\{\lambda_{i}\}_{i=1}^{k} λ={λi}i=1k,引入一个任务模糊数据集D来评价压缩大模型 f ( ⋅ ; θ , λ ) f(\cdot;\boldsymbol{\theta},\lambda) f(⋅;θ,λ)的性能,例如预训练数据集的子集。因此目标函数表示为
min λ ∈ V H ( λ ) = E ( x , y ) ∼ D h ( f ( x ; θ , λ ) , y ) s . t . Σ λ ≤ ρ (3) \begin{aligned}\min_{\lambda\in\mathcal{V}}H(\boldsymbol{\lambda})&=\mathbb{E}_{(x,y)\sim\mathcal{D}}h(f(x;\boldsymbol{\theta},\boldsymbol{\lambda}),y)\\&s.t.\Sigma\boldsymbol{\lambda}\leq\rho\end{aligned}\tag{3} λ∈VminH(λ)=E(x,y)∼Dh(f(x;θ,λ),y)s.t.Σλ≤ρ(3)
式中, ρ \rho ρ是模型的整体压缩比, h ( ⋅ , ⋅ ) h(\cdot,\cdot) h(⋅,⋅)是评价指标,但事实上,评价指标和低秩分配都是非常耗时耗算力的,所以这篇论文提出样本高效贝叶斯优化(BO)来优化公式3。这里引入一个替代模型(例如高斯模型 N ( μ ( ⋅ ) , σ 2 ( ⋅ ) ) \mathcal{N}(\mu(\cdot),\sigma^2(\cdot)) N(μ(⋅),σ2(⋅))),BO通过替代模型来估计目标函数 H ( λ ) H(\boldsymbol{\lambda}) H(λ),并且基于每一步的结果,更新后面一步的目标函数 H ( λ ) H(\boldsymbol{\lambda}) H(λ)。比如给出前t-1步 { λ 1 , ⋯ , λ t − 1 } \{\boldsymbol{\lambda}_{1},\cdots,\boldsymbol{\lambda}_{t-1}\} {λ1,⋯,λt−1}的目标函数值分别为 H t − 1 = [ H ( λ 1 ) , ⋯ , H ( λ t − 1 ) ] H_{t-1}=[H(\boldsymbol{\lambda}_{1}),\cdots,H(\boldsymbol{\lambda}_{t-1})] Ht−1=[H(λ1),⋯,H(λt−1)],替代模型更新为 μ ( λ ) = k ( K + η 2 I ) − 1 H t − 1 σ 2 ( λ ) = k ( λ , λ ) − k T ( K + η 2 I ) − 1 k (4) \mu(\boldsymbol{\lambda})=\boldsymbol{k}(\boldsymbol{K}+\eta^{2}\boldsymbol{I})^{-1}H_{t-1}\\\sigma^{2}(\boldsymbol{\lambda})=k(\boldsymbol{\lambda},\boldsymbol{\lambda})-\boldsymbol{k}^{T}(\boldsymbol{K}+\eta^{2}\boldsymbol{I})^{-1}\boldsymbol{k}\tag{4} μ(λ)=k(K+η2I)−1Ht−1σ2(λ)=k(λ,λ)−kT(K+η2I)−1k(4)
式中 k ( ⋅ , ⋅ ) k(\cdot,\cdot) k(⋅,⋅)是一个核函数, ( k = k ( λ , λ i ) ) i ∈ [ t − 1 ] (\boldsymbol{k}=k(\boldsymbol{\lambda},\boldsymbol{\lambda}_{i}))_{i\in[t-1]} (k=k(λ,λi))i∈[t−1], K = ( k ( λ i , λ j ) ) i , j ∈ [ t − 1 ] K = (k(\boldsymbol{\lambda}_{i},\boldsymbol{\lambda}_{j}))_{i,j\in[t-1]} K=(k(λi,λj))i,j∈[t−1], η 2 I \eta^{2}I η2I是用来模拟噪声的白核函数,得到后验估计 H ( λ ) H(\boldsymbol{\lambda}) H(λ)(例如 H ( λ ) ∼ N ( μ ( λ ) , σ 2 ( λ ) ) H(\boldsymbol{\lambda})\sim{\mathcal{N}}(\mu(\boldsymbol{\lambda}),\sigma^{2}(\boldsymbol{\lambda})) H(λ)∼N(μ(λ),σ2(λ)))之后,BO通过采集函数确定下一次的比率分布,对于采集函数,可以用EI
α ( λ ) = E H ( λ ) [ max { 0 , H ′ − H ( λ ) } ] λ t = a r g m a x λ α ( λ ) , (5) \begin{aligned}\alpha(\boldsymbol{\lambda})&=\mathbb{E}_{H(\boldsymbol{\lambda})}\left[\max\left\{0,H'-H(\boldsymbol{\lambda})\right\}\right]\\\boldsymbol{\lambda}_{t}&=\mathop{\mathrm{argmax}}_{\boldsymbol{\lambda}}\alpha(\boldsymbol{\lambda}),\end{aligned}\tag{5} α(λ)λt=EH(λ)[max{0,H′−H(λ)}]=argmaxλα(λ),(5)
式中, H ′ = min i ∈ [ t − 1 ] H ( λ i ) H^{\prime}=\operatorname*{min}_{i\in[t-1]}H(\boldsymbol{\lambda}_{i}) H′=mini∈[t−1]H(λi)是指迄今为止观察到的最小值,然后BO选择了最好的EI的方向去搜索。在得到最优比 λ ∗ \lambda^{*} λ∗之后,可以确定分配 r i = ( 1 − λ i ) d 1 d 2 / ( d 1 + d 2 ) r_{i}=(1-\lambda_{i})d_{1}d_{2}/(d_{1}+d_{2}) ri=(1−λi)d1d2/(d1+d2)。
1.3 后训练
为了不使模型参数量反弹,文章使用压缩模型的子空间对模型微调。
Y = ( B A + Λ b B r ′ Λ d A r ′ ) X (6) Y=(BA+\Lambda_bB_{r'}\Lambda_dA_{r'})X\tag{6} Y=(BA+ΛbBr′ΛdAr′)X(6)
式中, B r ′ ∈ R d 2 × r ′ B_{r^{\prime}}\in\mathbb{R}^{d_2\times r^{\prime}} Br′∈Rd2×r′, A r ′ ∈ R r ′ × d 1 A_{r^{\prime}}\in\mathbb{R}^{r^{\prime}\times d_1} Ar′∈Rr′×d1是修正后的 B B B和 A A A矩阵, Λ b \boldsymbol{\Lambda}_{b} Λb和 Λ d \boldsymbol{\Lambda}_{d} Λd是对角阵。
基于贝叶斯优化的自适应低秩分解 ↩︎
相关文章:

大模型压缩:基于贝叶斯优化的自适应低秩分解
1.方法 1.1 基于特征的高维空间低秩分解 PCA已经是老朋友了,每次一说主成分都会出现PCA。这篇文章1利用预训练数据的子集作为校准数据集 D c a l { x i } i 1 n \mathcal{D}_{cal}\{x_{i}\}_{i1}^{n} Dcal{xi}i1n,首先用校准数据集的样本协方差…...

【Python函数编程实战】:从基础到进阶,打造代码复用利器
文章目录 🚋前言🚀一、认识函数🌈二、函数定义❤️三、函数调用⭐四、实参与形参💥1. 形式参数🚲2. 实际参数🔥1. 位置参数☔2. 关键字参数🎬3. 默认参数🔥4. 可变数量参数(不定长参…...

ZooKeeper 应用场景深度解析
✨✨谢谢大家捧场,祝屏幕前的小伙伴们每天都有好运相伴左右,一定要天天开心哦!✨✨ 🎈🎈作者主页: 喔的嘛呀🎈🎈 目录 引言 1.…...

动手学深度学习(Pytorch版)代码实践 -计算机视觉-41目标检测数据集
41目标检测数据集 import os import pandas as pd import torch import torchvision import matplotlib.pylab as plt from d2l import torch as d2l# 数据集下载链接 # http://d2l-data.s3-accelerate.amazonaws.com/banana-detection.zip# 读取数据集 #save def read_data_b…...

2.2章节python的变量和常量
在Python中,变量和常量有一些基本的概念和用法,但需要注意的是,Python本身并没有内置的“常量”类型。然而,程序员通常会遵循一种约定,即使用全部大写的变量名来表示常量。 一、变量 在Python中,变量是一…...

豆包文科成绩超了一本线,为什么理科不行?
卡奥斯智能交互引擎是卡奥斯基于海尔近40年工业生产经验积累和卡奥斯7年工业互联网平台建设的最佳实践,基于大语言模型和RAG技术,集合海量工业领域生态资源方优质产品和知识服务,旨在通过智能搜索、连续交互,实时生成个性化的内容…...

Java多线程编程实践中的常见问题与解决方案
Java多线程编程实践中的常见问题与解决方案 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! **1. **引言 Java多线程编程是现代软件开发中不可或缺的一部分&a…...

WebStorm配置路径别名(jsconfig.json)
项目是 ViteVueTs 新建一个 jsconfig.json文件 {"compilerOptions": {"baseUrl": ".","paths": {"/*": ["./src/*"]}},"exclude": ["node_modules", "dist"] }然后在 vite.confi…...

[吃瓜教程]南瓜书第4章决策树
1.决策树的算法原理 从逻辑角度,条件判断语句的组合;从几何角度,根据某种准则划分特征空间; 是一种分治的思想,其最终目的是将样本约分约纯,而划分的核心是在条件的选择或者说是**特征空间的划分标准 ** …...

Redis 面试题完整指南:深度解析基础、进阶与高级功能
基础知识 1. 什么是Redis? Redis(Remote Dictionary Server)是一个开源的、基于内存的数据结构存储系统,既可以用作数据库、缓存,也可以用作消息中间件。它支持多种数据结构,如字符串、哈希、列表、集合、…...

spring 枚举、策略模式、InitializingBean初使化组合使用示例
实现一个简单的文本处理系统。 在这个系统中,我们将定义不同类型的文本处理策略,比如大小写转换、添加前缀后缀等,并使用工厂模式来管理这些策略。 1 定义一个枚举来标识不同的文本处理类型 public enum TextProcessTypeEnum {UPPER_CASE,LO…...

嵌入式学习——硬件(IIC、ADC)——day56
1. IIC 1.1 定义(同步串行半双工通信总线) IIC(Inter-Integrated Circuit)又称I2C,是是IICBus简称,所以中文应该叫集成电路总线。是飞利浦公司在1980年代为了让主板、嵌入式系统或手机用以连接低速周边设备…...

vCenter VXR01405C ALARM Certificate is about to expire
vCenter VXR01405C ALARM Certificate is about to expire 需要更新证书 步骤如下 ===vCenter=== root@vc [ ~ ]# for i in $(/usr/lib/vmware-vmafd/bin/vecs-cli store list); do echo STORE $i; sudo /usr/lib/vmware-vmafd/b STORE MACHINE_SSL_CERT Alias : __MACHINE…...
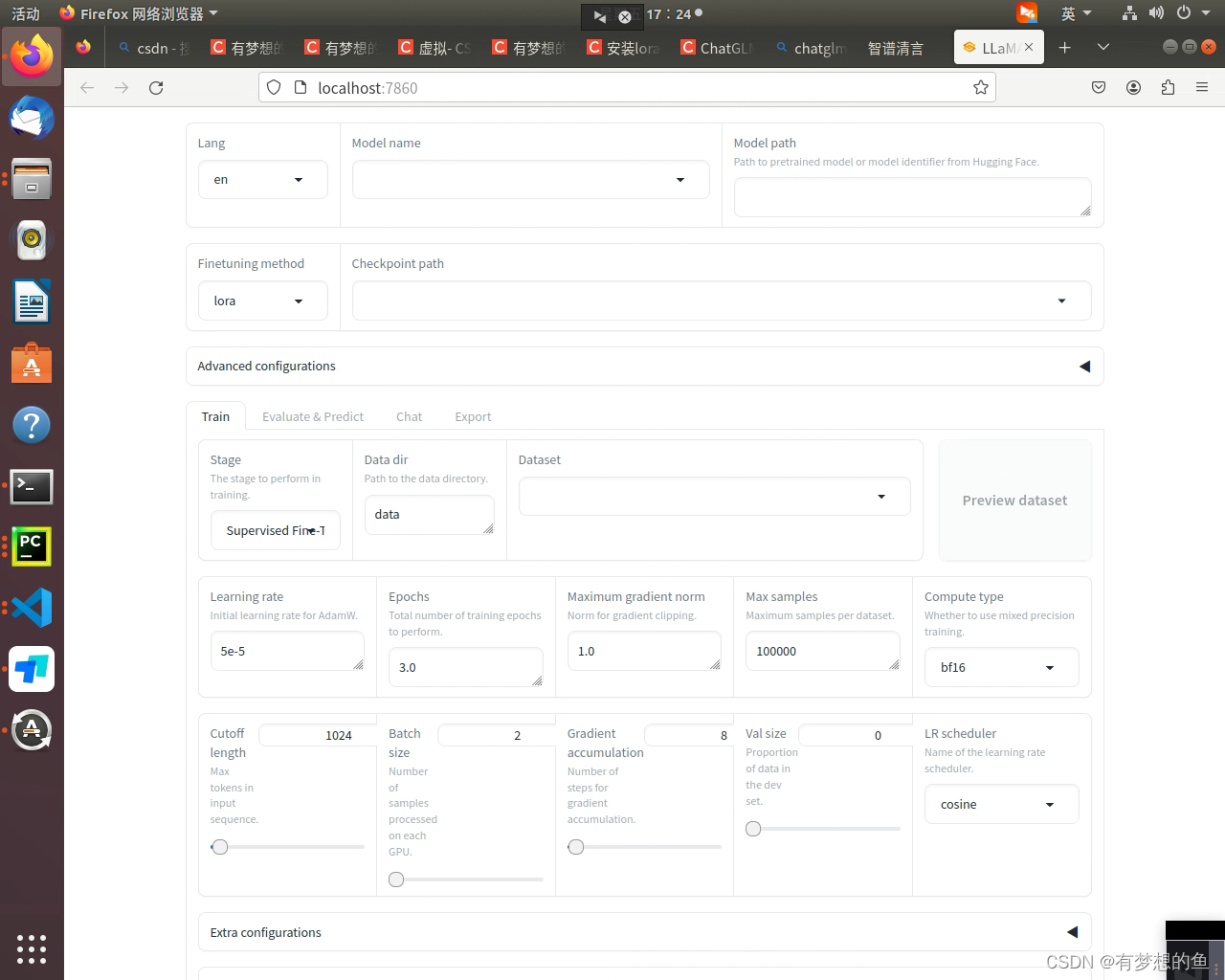
安装和微调大模型(基于LLaMA-Factory)
打开终端(在Unix或macOS上)或命令提示符/Anaconda Prompt(在Windows上)。 创建一个名为lora的虚拟环境并指定Python版本为3.9。 https://github.com/echonoshy/cgft-llm/blob/master/llama-factory/README.mdGitHub - hiyouga/…...

使用docker搭建squid和ss5
docker run -d --name squid-container -e TZAsia/Shanghai -p 自定义端口并记得开放:3128 ubuntu/squid docker exec -it squid-container /bin/bash apt update && apt install vim # 修改 http_port 3128 为 http_port 0.0.0.0:3128 # 修改 http_access deny all 为…...
)
大数据面试题之Flink(1)
目录 Flink架构 Flink的窗口了解哪些,都有什么区别,有哪几种?如何定义? Flink窗口函数,时间语义相关的问题 介绍下Flink的watermark(水位线),watermark需要实现哪个实现类,在何处定义?有什么作用? Flink的…...

策略模式、工厂模式和模板模式的应用
1、策略模式、工厂模式解决if else Cal package com.example.dyc.cal;import org.springframework.beans.factory.InitializingBean;public interface Cal extends InitializingBean {public Integer cal(Integer a, Integer b); }Cal工厂 package com.example.dyc.cal;impo…...
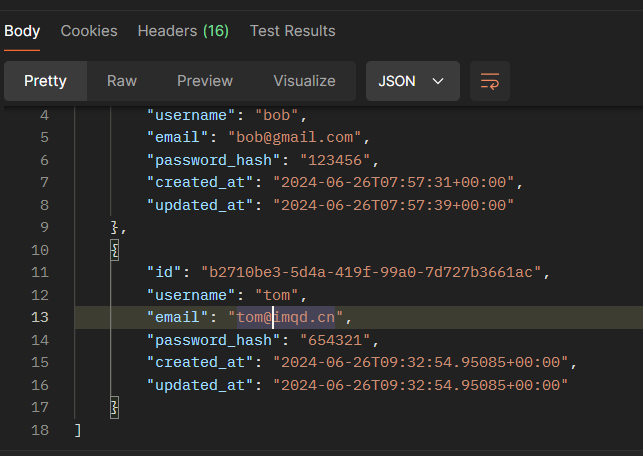
在postman中调试supabase的API接口
文章目录 在supabase中获取API地址和key知道它的restfull风格在postman中进行的设置1、get请求调试2、post新增用户调试3、使用patch更新数据,不用put!4、delete删除数据 总结 在supabase中获取API地址和key 首先登录dashboard后台,首页- 右…...

微信小程序毕业设计-英语互助系统项目开发实战(附源码+论文)
大家好!我是程序猿老A,感谢您阅读本文,欢迎一键三连哦。 💞当前专栏:微信小程序毕业设计 精彩专栏推荐👇🏻👇🏻👇🏻 🎀 Python毕业设计…...
【WEB前端2024】3D智体编程:乔布斯3D纪念馆-第49课-机器人自动跳舞
【WEB前端2024】3D智体编程:乔布斯3D纪念馆-第49课-机器人自动跳舞 使用dtns.network德塔世界(开源的智体世界引擎),策划和设计《乔布斯超大型的开源3D纪念馆》的系列教程。dtns.network是一款主要由JavaScript编写的智体世界引擎…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
