数据结构之二叉树概念
数据结构之二叉树
- 二叉树
- 简介
- 分类
- 普通二叉树
- 平衡二叉树
- 满二叉树
- 二叉搜索树(二叉排序树、二叉查找树),
- 平衡二叉树
- 红黑树
- B树类型
- B树(B-树、B_树)
- B+树
- B*树
二叉树
简介
二叉树(Binary Tree) :是一种非常重要的非线性结构。:二叉树是每个节点最多有两个子树的树结构;
是n(n>=0)个结点的有限集合,它或者是空树(n=0),或者是由一个根结点及两颗互不相交的、分别称为左子树和右子树的二叉树所组成
节点:Node, 二叉树是由N个节点组成,(每个节点有两个子节点的指针(也可以没有),分别为左子节点,右子节点)。
根节点:没有父节点的节点就是根节点(唯一),也就是第一层的哪一个节点。如图所示:4
叶子节点:没有子节点的节点就是叶子节点。如图所示:1,3,5,7
非叶子节点:有子节点的节点就是非叶子节点。如图所示:2,6,4(4 是根节点也是特殊的非叶子节点)
度:表示节点的子节点个数,因为子节点最大数量为2 (左子,右子),所以度最大为2.
高度:也称树的深度(层高)等,表示树的层级。如图所示:树高度为3.
每层节点数量:N = 2^(h-1) . N(每层数量),h (层级)。
树总节点数量:N = (2^h) - 1. N(每层数量),h (层级)。
如图所示
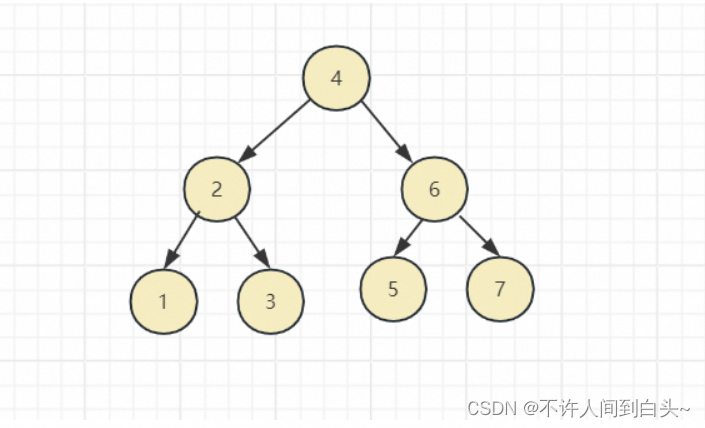
分类
二叉树也有类别:
普通二叉树
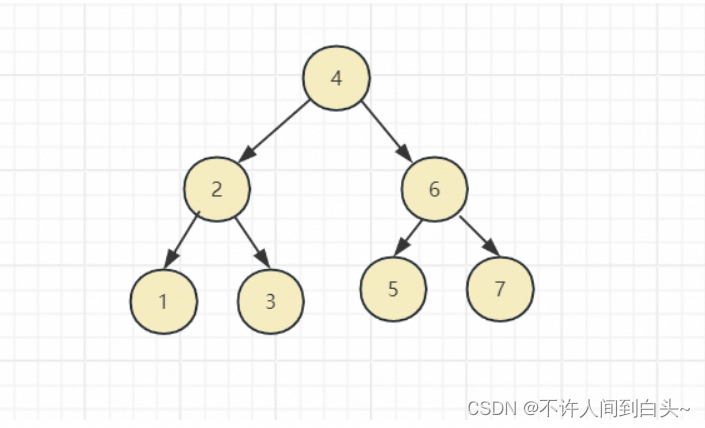
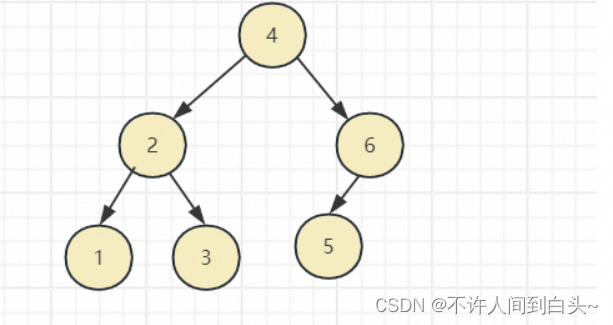
平衡二叉树
除最后一层外,每一层上的结点数均达到最大值;在最后一层上只缺少右边的若干结点
- 叶子结点只能出现在最下层和次下层。
- 最下层的叶子结点集中在树的左部。
- 倒数第二层若存在叶子结点,一定在右部连续位置。
- 如果结点度为1,则该结点只有左孩子,即没有右子树。
- 同样结点数目的二叉树,完全二叉树深度最小
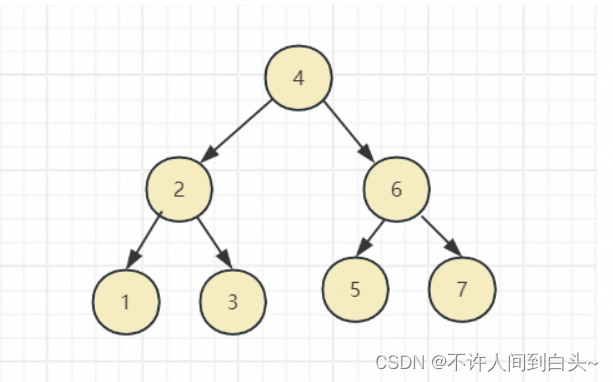
满二叉树
除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树
- 叶子只能出现在最下一层。出现在其它层就不可能达成平衡。
- 非叶子结点的度(
结点拥有的子树数目称为结点的度)一定是2 - 在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多
二叉搜索树(二叉排序树、二叉查找树),
二叉排序树:可以为空树,或者是具备如下性质:若它的左子树不空,则左子树上的所有结点的值均小于根节点的值;若它的右子树不空,则右子树上的所有结点的值均大于根节点的值,左右子树分别为二叉排序树。
如下图所示
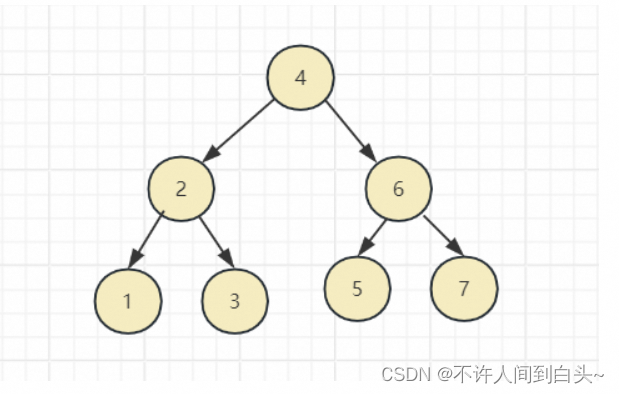
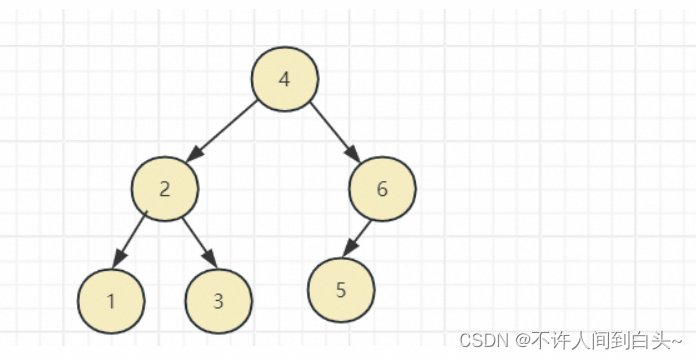
平衡二叉树
平衡二叉树是一种概念,是二叉查找树的一个进化体,它有几种实现方式:红黑树、AVL树
它是一个空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是平衡二叉树,如果插入或者删除一个节点使得高度之差大于1,就要进行节点之间的旋转,将二叉树重新维持在一个平衡状态。
这个方案很好的解决了二叉查找树退化成链表的问题,把插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间,不过相对二叉查找树来说,时间上稳定了很多
AVL实现平衡的关键在于旋转操作:
插入和删除可能破坏二叉树的平衡,此时需要通过一次或多次树旋转来重新平衡这个树。
当插入数据时,最多只需要1次旋转(单旋转或双旋转);但是当删除数据时,会导致树失衡,AVL需要维护从被删除节点到根节点这条路径上所有节点的平衡,旋转的量级为O(lgn)
由于旋转的耗时,AVL树在删除数据时效率很低;在删除操作较多时,维护平衡所需的代价可能高于其带来的好处,因此AVL实际使用并不广泛
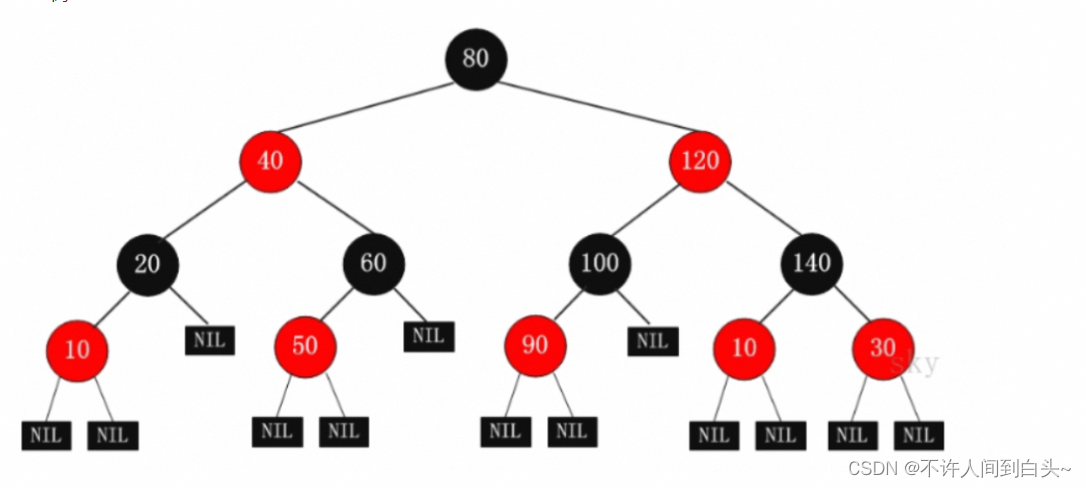
红黑树
红黑树是一种平衡二叉查找树的变体,它的左右子树高差有可能大于1,所以红黑树不是严格意义上的平衡二叉树(AVL),但对之进行平衡的代价较低, 其平均统计性能要强于 AVL
- 每个节点或者是黑色,或者是红色
- 根节点是黑色
- 每个叶结点是黑色
- 如果一个节点是红色的,则它的子节点必须是黑色的,红色节点的孩子和父亲都不能是红色。从每个叶子到根的所有路径上不能有两个连续的红色节点,任意一结点到每个叶子结点的路径都包含数量相同的黑结点。确保没有一条路径会比其他路径长出俩倍。因而,红黑树是相对接近平衡的二叉树,并不是一个完美平衡二叉查找树
红黑树和AVL树区别
RB-Tree和AVL树作为二叉搜索树(BBST),其实现的算法时间复杂度相同,AVL作为最先提出的BBST,貌似RB-tree实现的功能都可以用AVL树是代替,那么为什么还需要引入RB-Tree呢
- 红黑树不追求
完全平衡,即不像AVL那样要求节点的高度差的绝对值<= 1,它只要求部分达到平衡,但是提出了为节点增加颜色,红黑是用非严格的平衡来换取增删节点时候旋转次数的降低,任何不平衡都会在三次旋转之内解决,而AVL是严格平衡树,因此在增加或者删除节点的时候,根据不同情况,旋转的次数比红黑树要多 - 就插入节点导致树失衡的情况,
AVL和RB-Tree都是最多两次树旋转来实现复衡rebalance,旋转的量级是O(1) - 删除节点导致失衡,
AVL需要维护从被删除节点到根节点root这条路径上所有节点的平衡,旋转的量级为O(logN),而RB-Tree最多只需要旋转3次实现复衡,只需O(1),所以说RB-Tree删除节点的rebalance的效率更高,开销更小 AVL的结构相较于RB-Tree更为平衡,插入和删除引起失衡,RB-Tree复衡效率更高;当然,由于AVL高度平衡,因此AVL的Search效率更高- 针对插入和删除节点导致失衡后的
rebalance操作,红黑树能够提供一个比较便宜的解决方案,降低开销,是对search,insert,以及delete效率的折衷,总体来说,RB-Tree的统计性能高于AVL - 故引入
RB-Tree是功能、性能、空间开销的折中结果
AVL更平衡,结构上更加直观,时间效能针对读取而言更高;维护稍慢,空间开销较大。
红黑树,读取略逊于AVL,维护强于AVL,空间开销与AVL类似,内容极多时略优于AVL,维护优于AVL。
缺点:对于数据在内存中的情况,红黑树的表现是非常优异的。但是对于数据在磁盘等辅助存储设备中的情况(如MySQL等数据库),红黑树并不擅长,因为红黑树长得还是太高了。当数据在磁盘中时,磁盘IO会成为最大的性能瓶颈,设计的目标应该是尽量减少IO次数;而树的高度越高,增删改查所需要的IO次数也越多,会严重影响性能
总结:实际应用中,若搜索的次数远远大于插入和删除,那么选择AVL,如果搜索,插入删除次数几乎差不多,应该选择RB-Tree
B树类型
B树(B-树、B_树)
一种平衡的多叉树,称为B树(或B-树、B_树,B:balanced说明B树和平衡树有关系)
B树是为磁盘等辅存设备设计的多路平衡查找树,与二叉树相比,B树的每个非叶节点可以有多个子树。 因此,当总节点数量相同时,B树的高度远远小于AVL树和红黑树(B树是一颗“矮胖子”),磁盘IO次数大大减少。
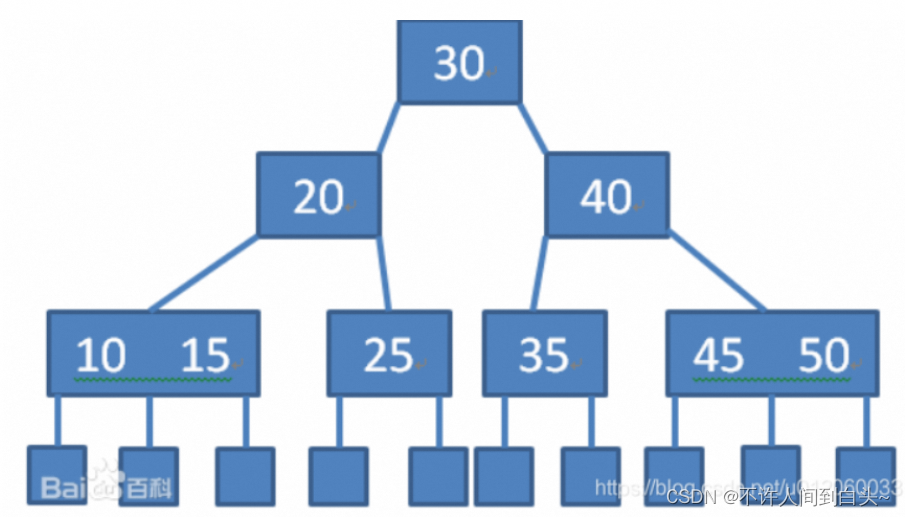
一棵M阶B树(M阶数:表示此树的结点最多有多少个孩子结点(子树))是一棵平衡的m路搜索树。它或者是空树,或者是满足下列性质的树:
- 每个节点最多包含 m 个子节点
- 根结点至少有两个子节点,除根节点外,每个非叶节点至少包含 m/2 个子节点;
- 拥有 k 个子节点的非叶节点将包含 k - 1 条记录
- 每个非根节点所包含的关键字个数 j 满足:┌m/2┐ - 1 <= j <= m - 1;
- 除根结点以外的所有结点(不包括叶子结点)的度数正好是关键字总数加1,故内部子树个数 k 满足:┌m/2┐ <= k <= m ;
- 所有的叶子结点都位于同一层。
简单理解为:平衡多叉树为B树(每一个子节点上都是有数据的),叶子节点之间无指针相邻
B树的搜索,从根结点开始,如果查询的关键字与结点的关键字相等,那么就命中;否则,如果查询关键字比结点关键字小,就进入左儿子;如果比结点关键字大,就进入右儿子;如果左儿子或右儿子的指针为空,则报告找不到相应的关键字;重复,直到所对应的儿子指针为空,或已经是叶子结点
如果B树的所有非叶子结点的左右子树的结点数目均保持差不多(平衡),那么B树的搜索性能逼近二分查找;但它比连续内存空间的二分查找的优点是,改变B树结构(插入与删除结点)不需要移动大段的内存数据,甚至通常是常数开销;但B树在经过多次插入与删除后,有可能导致不同的结构
B-树的特性:
- 关键字集合分布在整颗树中;
- 任何一个关键字出现且只出现在一个结点中;
- 搜索有可能在非叶子结点结束;
- 其搜索性能等价于在关键字全集内做一次二分查找;
- 自动层次控制;
由于M阶B树每个结点最少M/2个结点的限制,是为了最大限度的减少查找路径的长度,提供查找效率
B树在数据库中有一些应用,如mongodb的索引使用了B树结构。但是在很多数据库应用中,使用了是B树的变种B+树
B+树
B+树是B树的一种变形形式,B+树上的叶子结点存储关键字以及相应记录的地址,叶子结点以上各层作为索引使用。一棵m阶的B+树定义如下
- 每个结点至多有m个子女;
- 除根结点外,每个结点至少有[m/2]个子女,根结点至少有两个子女;
- 有k个子女的结点必有k个关键字
B+树的查找与B树不同,当索引部分某个结点的关键字与所查的关键字相等时,并不停止查找,应继续沿着这个关键字左边的指针向下,一直查到该关键字所在的叶子结点为止。
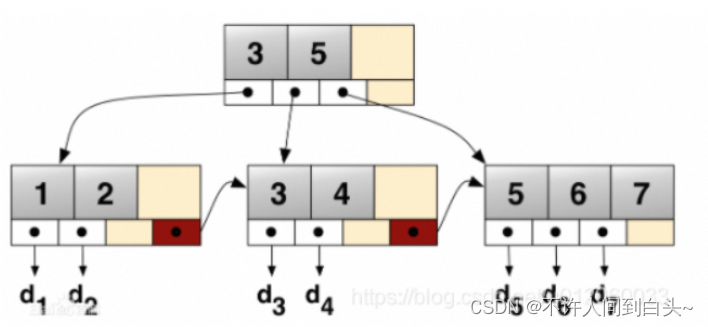
B+树也是多路平衡查找树,其与B树的区别主要在于:
B树中每个节点(包括叶节点和非叶节点)都存储真实的数据,B+树中只有叶子节点存储真实的数据,非叶节点只存储键。
在MySQL中,这里所说的真实数据,可能是行的全部数据(如Innodb的聚簇索引),也可能只是行的主键(如Innodb的辅助索引),或者是行所在的地址(如MyIsam的非聚簇索引)
点击了解MySQL中索引数据结构分析B树中一条记录只会出现一次,不会重复出现,而B+树的键则可能重复重现——一定会在叶节点出现,也可能在非叶节点重复出现。B+树的叶节点之间通过双向链表链接B树中的非叶节点,记录数比子节点个数少1;而B+树中记录数与子节点个数相同。
由此,B+树与B树相比,有以下优势:
- 更少的
IO次数:B+树的非叶节点只包含键,而不包含真实数据,因此每个节点存储的记录个数比B树多很多(即阶m更大),因此B+树的高度更低,访问时所需要的IO次数更少。此外,由于每个节点存储的记录数更多,所以对访问局部性原理的利用更好,缓存命中率更高。 - 更适于范围查询:在
B树中进行范围查询时,首先找到要查找的下限,然后对B树进行中序遍历,直到找到查找的上限;而B+树的范围查询,只需要对链表进行遍历即可。 - 更稳定的查询效率:
B树的查询时间复杂度在1到树高之间(分别对应记录在根节点和叶节点),而B+树的查询复杂度则稳定为树高,因为所有数据都在叶节点。
B+树也存在劣势:由于键会重复出现,因此会占用更多的空间。但是与带来的性能优势相比,空间劣势往往可以接受,因此B+树的在数据库中的使用比B树更加广泛。
B*树
B*树是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针;
B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3(代替B+树的1/2);
B+树的分裂:当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针;
B*树的分裂:当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针;所以,B*树分配新结点的概率比B+树要低,空间使用率更高
B树类型总结:
二叉搜索树:二叉树,每个结点只存储一个关键字,等于则命中,小于走左结点,大于走右结点;B树(B-树):多路搜索树,每个结点存储M/2到M(M是指M阶B树)个关键字,非叶子结点存储指向关键字范围的子结点;所有关键字在整颗树中出现,且只出现一次,非叶子结点可以命中;B+树:在B-树基础上,为叶子结点增加链表指针,所有关键字都在叶子结点中出现,非叶子结点作为叶子结点的索引;B+树总是到叶子结点才命中;B*树:在B+树基础上,为非叶子结点也增加链表指针,将结点的最低利用率从1/2提高到2/3
相关文章:

数据结构之二叉树概念
数据结构之二叉树 二叉树简介分类普通二叉树平衡二叉树满二叉树二叉搜索树(二叉排序树、二叉查找树),平衡二叉树红黑树 B树类型B树(B-树、B_树)B树B*树 二叉树 简介 二叉树(Binary Tree) :是一种非常重要…...
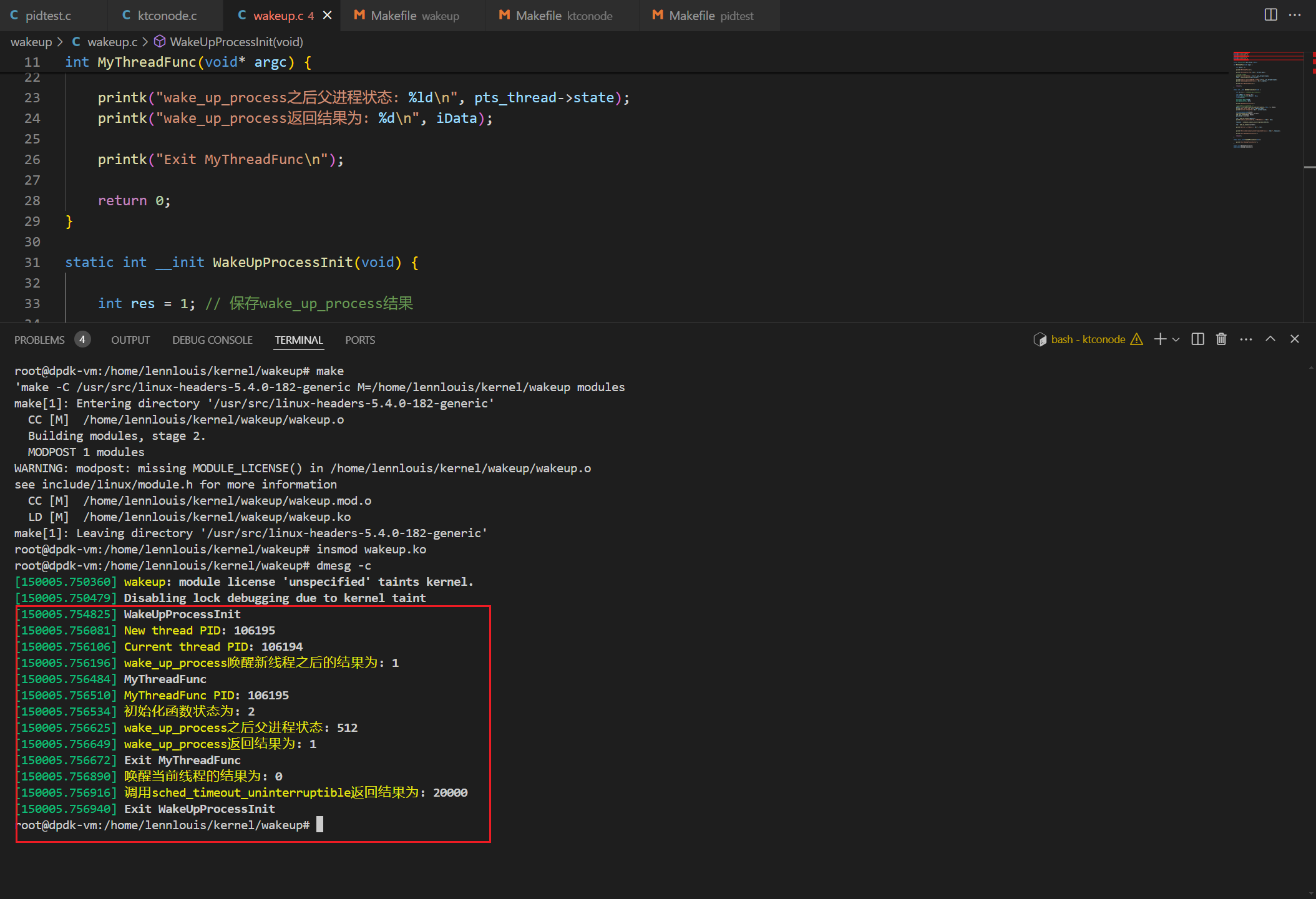
Linux源码阅读笔记08-进程调度API系统调用案例分析
kthread_create_on_node kthread_create_on_node函数功能:指定存储节点创建新内核线程。源码如下: 操作实战 #include <linux/module.h> #include <linux/pid.h> #include <linux/sched.h> #include <linux/kthread.h> #inclu…...

短视频抓取:成都柏煜文化传媒有限公司
短视频抓取:技术挑战、法律边界与未来趋势 随着移动互联网的迅猛发展,短视频平台如雨后春笋般涌现,成为现代人生活娱乐的重要组成部分。然而,在海量短视频内容中,如何高效、准确地抓取目标视频,成为了一个…...

proto的前后端使用
首先定义一个input.proto文件 内容如下 syntax "proto3";message InputData {int32 UserId 1; // 将 number 改为 int32 或 int64string UserInput 2;string DrunkState 3; }message ResponseData {string AIResponse 1;string prompt 2;string emoti…...

华为解决固态硬盘致命弱点:延长30~50%的SSD寿命
如今的SSD容量越做越大,企业级SSD容量已达30TB、60TB的、甚至120TB。但SSD寿命一直是“致命伤”,越大容量的盘,出现故障后,丢失的数据就越多。 近日, 华为数据存储发文,揭开华为全闪分布式存储让SSD大盘更“…...

登录验证码高扩展性设计方案
登录验证码高扩展性建设方案 本文分享了一种登录验证码高扩展性的建设方案,通过工厂模式策略模式,增强了验证码服务中验证码生成器、验证码存储器、验证码图片生成器的扩展性,实现了服务组件的多样化,降低了维护成本 登录验证码高…...
普通字符串的回写)
Spring MVC数据绑定和响应——数据回写(一)普通字符串的回写
接下来通过HttpServletResponse输出数据的案例,演示普通字符串的回写,案例具体实现步骤如下。 1、创建一个数据回写类DataController,在DataController类中定义showDataByResponse()方法,用于测试在Spring MVC中普通字符串的回写…...

怎样才能更好地保护个人账号的安全
怎样才能更好地保护个人账号的安全 保护个人账号安全是网络安全的重要组成部分,以下是一些有效的措施来增强账号的安全性: 1. 使用强密码 复杂性:创建包含大小写字母、数字和特殊字符的密码。长度:密码至少应有12个字符长。唯一…...

react native优质开源项目
React Native 是一个非常流行的用于构建跨平台移动应用程序的框架,开源社区贡献了许多优质的项目和库。以下是一些备受认可的 React Native 开源项目,适合用来学习和参考: ### 1. **React Native Elements** [React Native Elements](https:…...

速盾:海外cdn有哪些优缺点呢?
海外 CDN(内容分发网络)是一种通过在全球多个节点上分布内容来加速网站访问速度的服务。它通过将网站的静态内容缓存到全球各地的服务器上,使用户可以从最近的服务器获取内容,从而提高网站的响应速度和用户体验。然而,…...
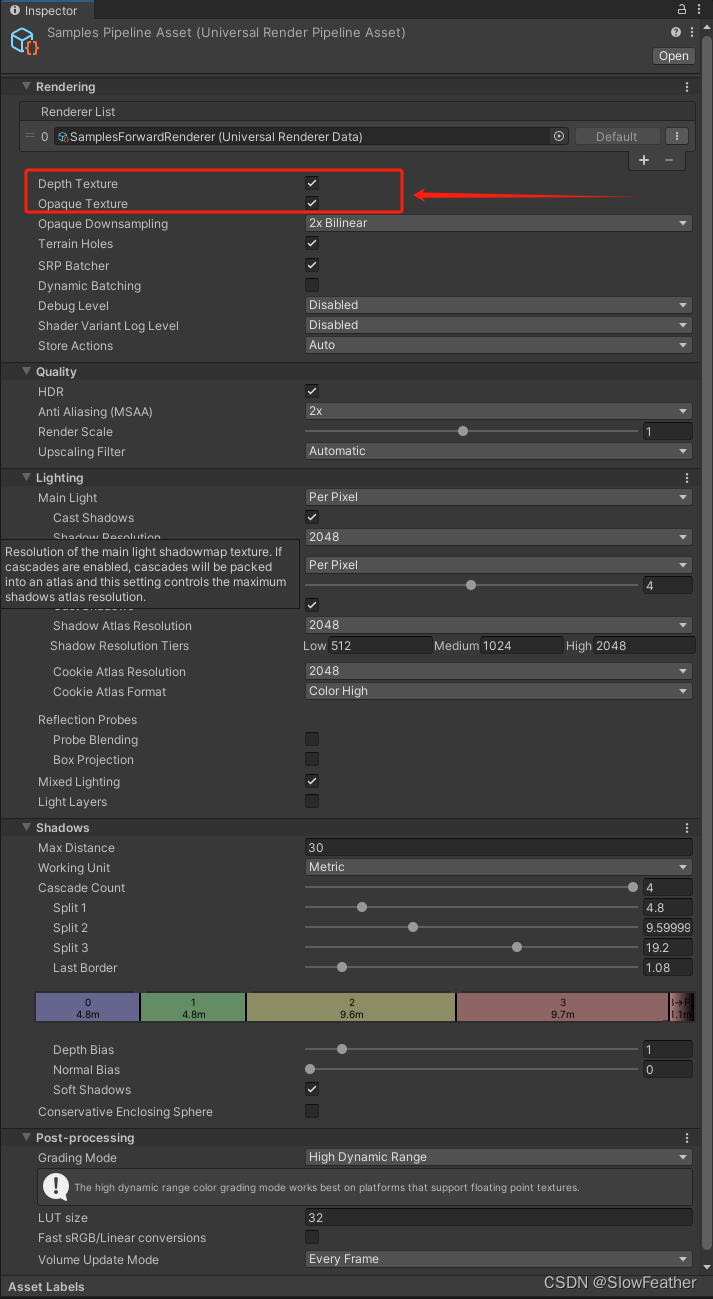
Unity Shader 软粒子
Unity Shader 软粒子 前言项目Shader连连看项目渲染管线设置 鸣谢 前言 当场景有点单调的时候,就需要一些粒子点缀,此时软粒子就可以发挥作用了。 使用软粒子与未使用软粒子对比图 项目 Shader连连看 这里插播一点,可以用Vertex Color与…...

nextTick的应用和原理理解
一.代码的理解 <template><div id"app"><div></div><button click"fn" ref"box"> {{ name }}</button></div> </template><script> export default {data: function () {return {n…...

.Net Core 微服务之Consul
目录 一、微服务架构 vs 单体架构 1. 单体架构介绍 2. 微服务架构介绍 3. 微服务架构 vs 单体架构的区别 4. 适用场景和选择 4.1 微服务架构的适用场景和选择 复杂度和规模需求高的应用程序: 技术栈的灵活性需求: 快速迭代和持续交付: 高可用性和容错性的要求: 4…...

速盾:cdn流量调度
CDN(Content Delivery Network)是指内容分发网络,它是一种通过部署在不同地理位置的服务器来传递互联网内容的技术。CDN的主要目标是通过将内容放置在离用户最近的服务器上,来提高用户访问网站的响应速度和性能。 CDN的流量调度是…...

Windows批处理入门:快速掌握批处理脚本的基本技巧
一、前言 在Windows操作系统中,批处理文件(Batch File)是一种非常实用的工具,它允许用户通过简单的命令行脚本来自动化各种任务。无论是系统管理员、开发人员,还是普通用户,掌握批处理文件的基本知识都能极…...

【C++之unordered_set和unordered_map的模拟实现】
C学习笔记---025 C之unordered_set和unordered_map的模拟实现1、unordered_set的模拟实现2、unordered_map的模拟实现 C之unordered_set和unordered_map的模拟实现 前言: 前面篇章学习了C对unordered_set和unordered_map的认识和应用,接下来继续学习&am…...

服务器使用别人的conda
很多台机器都共用一个conda时候,可以在conda的bin目录下运行./conda init来使得该环境机器用这个conda作为默认的conda。 但是有个环境报错: -bash: ./conda: /apdcephfs_cq8/share_1367250/jaimeji/anaconda/jaime_conda/bin/python: bad interpreter:…...

农村程序员陈随易2024年中总结
今天是 2024年7月1日,时间如白驹过隙,今年已去其一半。 总结一下今年上半年的情况,给大家提供一些参考和建议。 希望大家关注一下公众号 陈随易,有些内容只在公众号发表。 先看看我的年初计划,这个在今年年初的时候&…...

Spring Boot中的日志管理最佳实践
Spring Boot中的日志管理最佳实践 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们来探讨一下在Spring Boot应用中如何有效管理日志,确保系统…...

python基础语法 004-2流程控制- for遍历
1 遍历 1.1 什么是遍历? 可以遍历的元素:字符串、列表、元组、字典、集合字符串是可以进行for 循环。(容器对象,序列)可迭代对象iterable 例子: 1 )、for遍历字符串: name xiao…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
