第十四届蓝桥杯省赛C++B组E题【接龙数列】题解(AC)




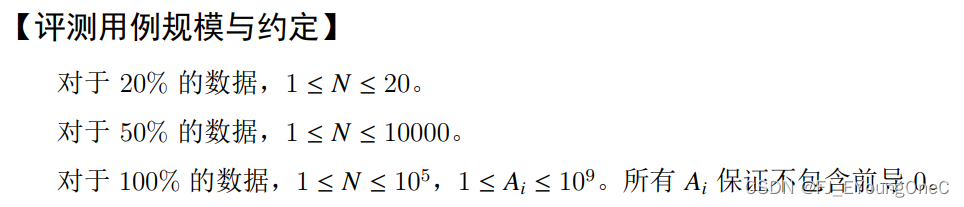
需求分析
题目要求最少删掉多少个数后,使得数列变为接龙数列。
相当于题目要求求出数组中的最长接龙子序列。
题目分析
对于一个数能不能放到接龙数列中,只关系到这个数的第一位和最后一位,所以我们可以先对数组进行预处理,将所有的数变为两位数,例如 12345 → 15 12345 \rightarrow 15 12345→15, 6 → 66 6 \rightarrow 66 6→66, … \dots …,这样当我们需要取出一个数 x x x 的第一位时,只需要计算 x / 10 x / 10 x/10,取出最后一位时,只需要计算 x % 10 x \% 10 x%10。
那么接下来考虑如何求接龙序列的最大值。
考虑动态规划, f ( i , j ) f(i, j) f(i,j) 表示在前 i i i 个数中,以 j j j 结尾的最大长度。
考虑状态转移,设第 i i i 个数为 a b ab ab:
- 若不选第 i i i 个数,则有 f ( i , j ) = f ( i − 1 , j ) f(i, j) = f(i - 1, j) f(i,j)=f(i−1,j)( 0 ≤ j ≤ 9 0 \leq j \leq 9 0≤j≤9)。
- 若选第 i i i 个数,则 f ( i , b ) = max ( f ( i − 1 , b ) , f ( i − 1 , a ) + 1 ) f(i, b) = \max(f(i - 1, b), f(i - 1, a) + 1) f(i,b)=max(f(i−1,b),f(i−1,a)+1)
那么接龙数列的最大长度为 max ( { f ( n , i ) \max(\{f(n, i) max({f(n,i)( 0 ≤ i ≤ 9 0 \leq i \leq 9 0≤i≤9) } ) \}) })。
观察状态转移发现, f ( i , j ) f(i, j) f(i,j) 仅由 f ( i − 1 , x ) f(i - 1, x) f(i−1,x) 计算得出,故可以使用滚动数组进行优化。
时间复杂度 O ( n ) O(n) O(n)。
- C++
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1e5 + 10;int n;
int q[N];
int f[N][10];int main()
{cin >> n;for (int i = 1; i <= n; ++ i ){int x;cin >> x;int y = x % 10;while (x >= 10)x /= 10;q[i] = x * 10 + y;}for (int i = 1; i <= n; ++ i ){for (int j = 0; j < 10; ++ j )f[i][j] = f[i - 1][j];int a = q[i] / 10, b = q[i] % 10;f[i][b] = max(f[i][b], f[i - 1][a] + 1);}int res = 0;for (int i = 0; i < 10; ++ i )res = max(res, f[n][i]);cout << n - res << endl;return 0;
}
- C++(空间优化)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1e5 + 10;int n;
int q[N];
int f[N];int main()
{cin >> n;for (int i = 0; i < n; ++ i ){int x;cin >> x;int y = x % 10;while (x >= 10)x /= 10;q[i] = x * 10 + y;}for (int i = 0; i < n; ++ i ){int a = q[i] / 10, b = q[i] % 10;f[b] = max(f[b], f[a] + 1);}cout << n - *max_element(f, f + 10) << endl;return 0;
}
【在线测评】
相关文章:

第十四届蓝桥杯省赛C++B组E题【接龙数列】题解(AC)
需求分析 题目要求最少删掉多少个数后,使得数列变为接龙数列。 相当于题目要求求出数组中的最长接龙子序列。 题目分析 对于一个数能不能放到接龙数列中,只关系到这个数的第一位和最后一位,所以我们可以先对数组进行预处理,将…...

Ubuntu 20.04.4 LTS 离线安装docker 与docker-compose
Ubuntu 20.04.4 LTS 离线安装docker 与docker-compose 要在Ubuntu 20.04.4 LTS上离线安装Docker和Docker Compose,你需要首先从有网络的环境下载Docker和Docker Compose的安装包,然后将它们传输到离线的服务器上进行安装。 在有网络的环境中:…...

vue3+ts 写echarts 中国地图
需要引入二次封装的echarts和在ts文件写的option <template><div class"contentPage"><myEcharts :options"chartOptions" class"myEcharts" id"myEchartsMapId" ref"mapEcharts" /></di…...
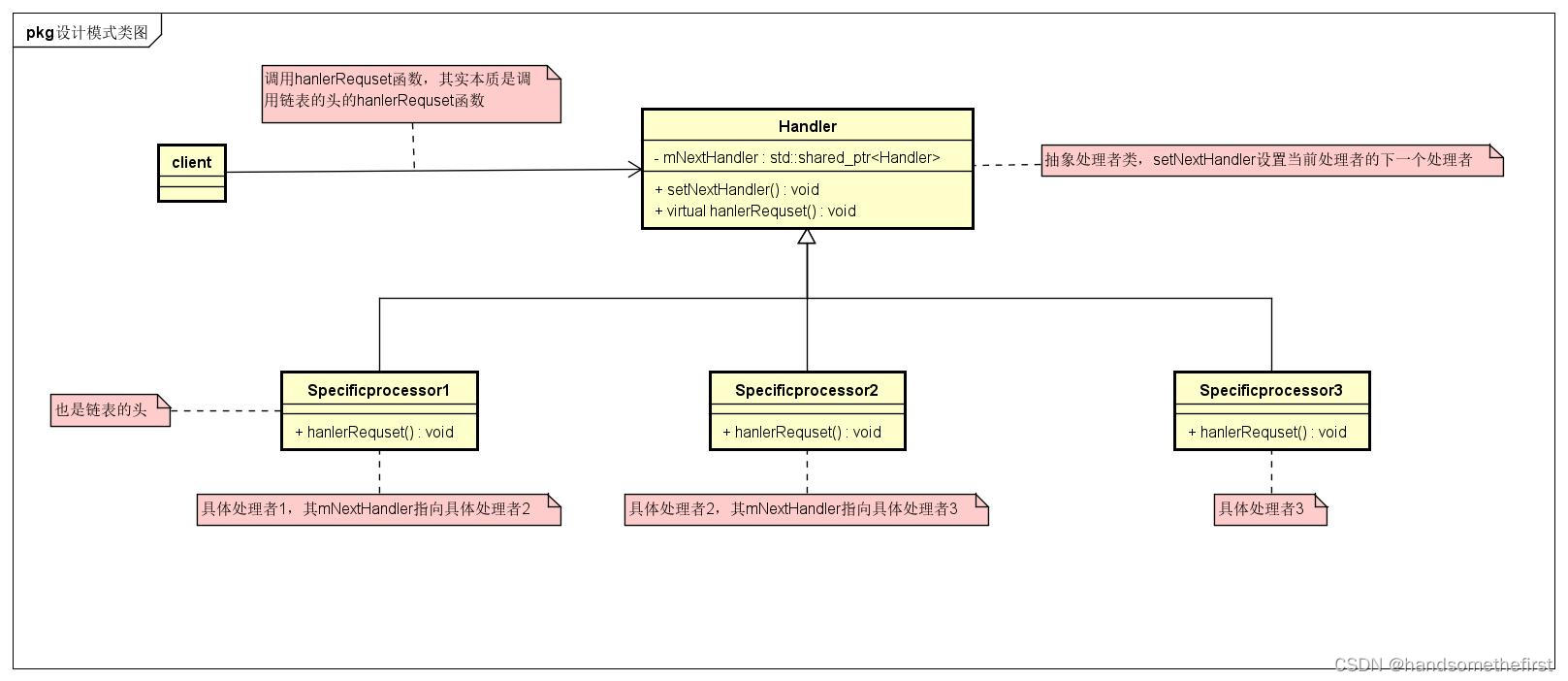
【设计模式】【行为型模式】【责任链模式】
系列文章目录 可跳转到下面链接查看下表所有内容https://blog.csdn.net/handsomethefirst/article/details/138226266?spm1001.2014.3001.5501文章浏览阅读2次。系列文章大全https://blog.csdn.net/handsomethefirst/article/details/138226266?spm1001.2014.3001.5501 目录…...
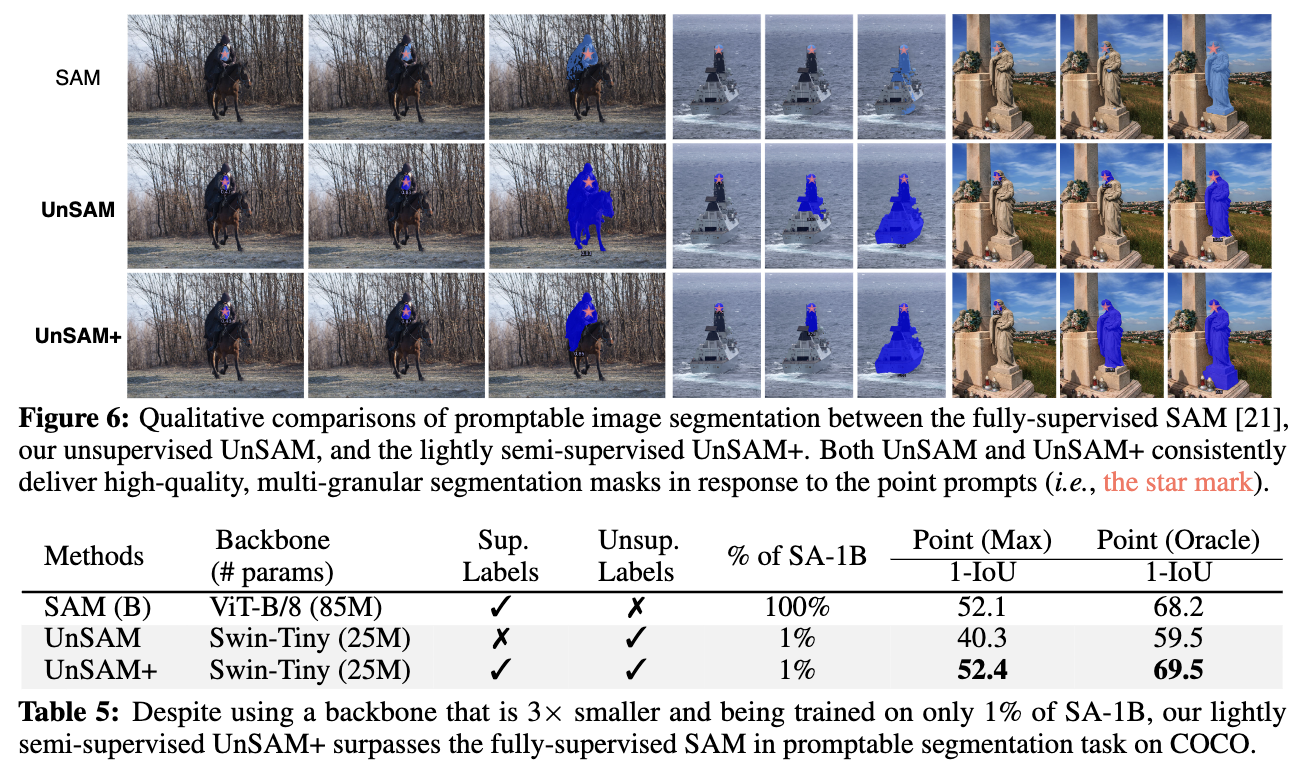
超越所有SOTA达11%!媲美全监督方法 | UC伯克利开源UnSAM
文章链接:https://arxiv.org/pdf/2406.20081 github链接:https://github.com/frank-xwang/UnSAM SAM 代表了计算机视觉领域,特别是图像分割领域的重大进步。对于需要详细分析和理解复杂视觉场景(如自动驾驶、医学成像和环境监控)的应用特别有…...
)
享元模式(设计模式)
享元模式(Flyweight Pattern)是一种结构型设计模式,它通过共享细粒度对象来减少内存使用,从而提高性能。在享元模式中,多个对象可以共享相同的状态以减少内存消耗,特别适合用于大量相似对象的场景。 享元模…...
【机器学习】大模型训练的深入探讨——Fine-tuning技术阐述与Dify平台介绍
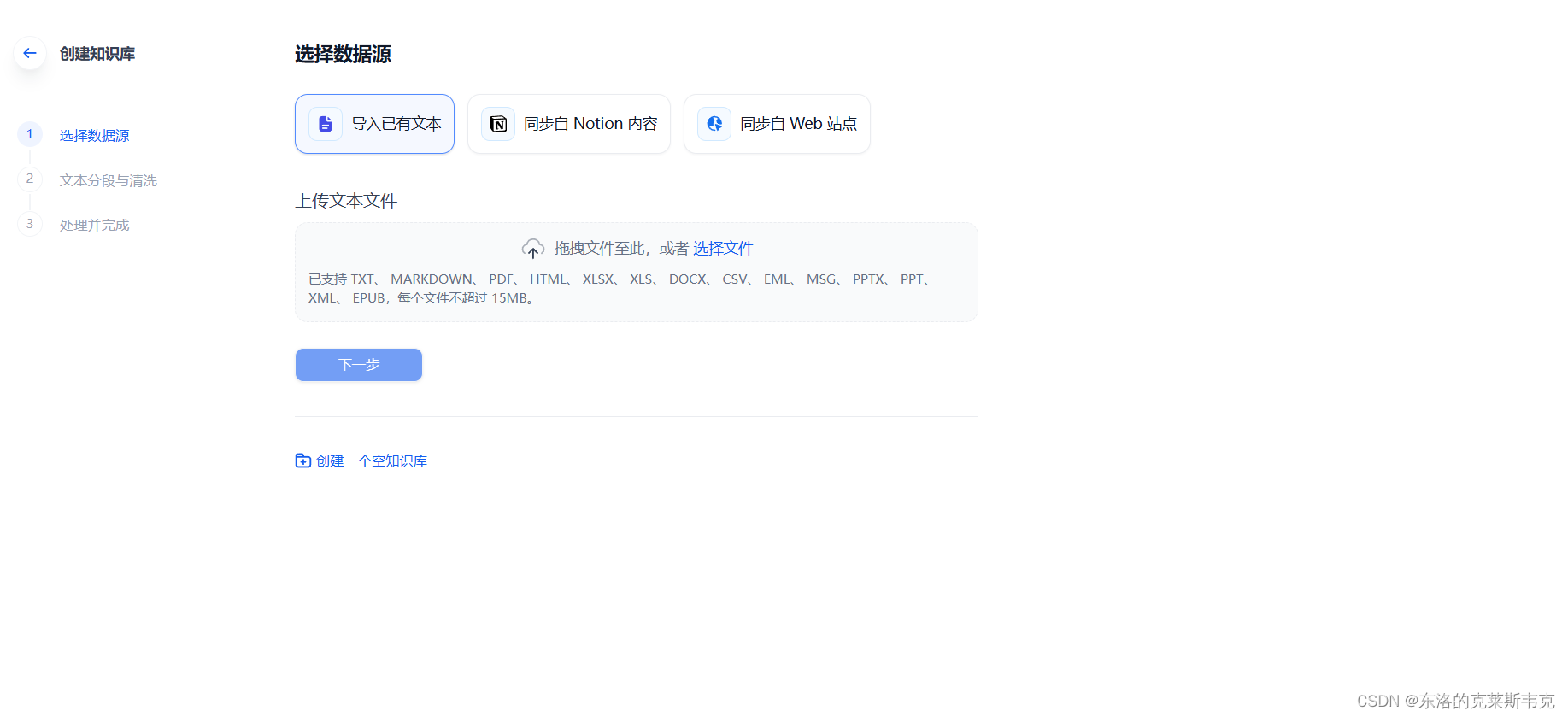
目录 引言 Fine-tuning技术的原理阐 预训练模型 迁移学习 模型初始化 模型微调 超参数调整 任务设计 数学模型公式 Dify平台介绍 Dify部署 创建AI 接入大模型api 选择知识库 个人主页链接:东洛的克莱斯韦克-CSDN博客 引言 Fine-tuning技术允许用户根…...
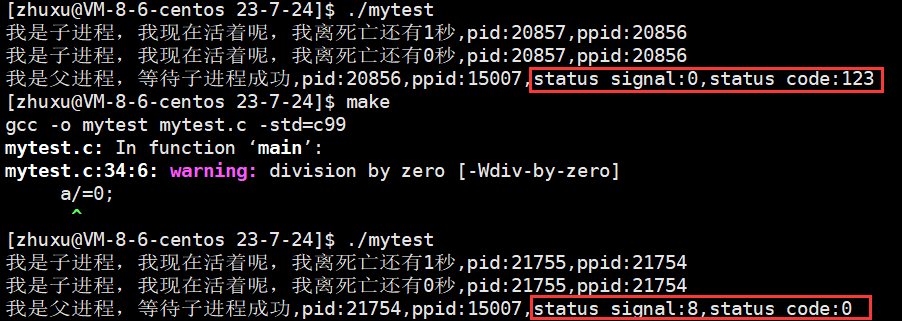
【Linux从入门到放弃】探究进程如何退出以进程等待的前因后果
🧑💻作者: 情话0.0 📝专栏:《Linux从入门到放弃》 👦个人简介:一名双非编程菜鸟,在这里分享自己的编程学习笔记,欢迎大家的指正与点赞,谢谢! 进…...

QT5 static_cast实现显示类型转换
QT5 static_cast实现显示类型转换,解决信号重载情况...
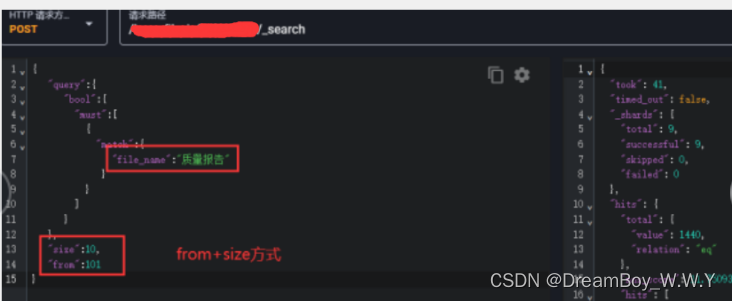
【ES】--Elasticsearch的翻页详解
目录 一、前言二、from+size浅分页1、from+size导致深度分页问题三、scroll深分页1、scroll原理2、scroll可以返回总计数量四、search_after深分页1、search_after避免深度分页问题一、前言 ES的分页常见的主要有三种方式:from+size浅分页、scroll深分页、search_after分页。…...

3.js - 纹理的重复、偏移、修改中心点、旋转
你瞅啥 上字母 // ts-nocheck // 引入three.js import * as THREE from three // 导入轨道控制器 import { OrbitControls } from three/examples/jsm/controls/OrbitControls // 导入lil.gui import { GUI } from three/examples/jsm/libs/lil-gui.module.min.js // 导入twee…...

RS232隔离器的使用
RS232隔离器在通信系统中扮演着至关重要的角色,其主要作用可以归纳如下: 一、保护通信设备 电气隔离:RS232隔离器通过光电隔离技术,将RS-232接口两端的设备电气完全隔离,从而避免了地线回路电压、浪涌、感应雷击、静电…...

一切为了安全丨2024中国应急(消防)品牌巡展武汉站成功召开!
消防品牌巡展武汉站 6月28日,由中国安全产业协会指导,中国安全产业协会应急创新分会、应急救援产业网联合主办,湖北消防协会协办的“一切为了安全”2024年中国应急(消防)品牌巡展-武汉站成功举办。该巡展旨在展示中国应急(消防&am…...

【面试系列】PHP 高频面试题
欢迎来到我的博客,很高兴能够在这里和您见面!欢迎订阅相关专栏: ⭐️ 全网最全IT互联网公司面试宝典:收集整理全网各大IT互联网公司技术、项目、HR面试真题. ⭐️ AIGC时代的创新与未来:详细讲解AIGC的概念、核心技术、…...
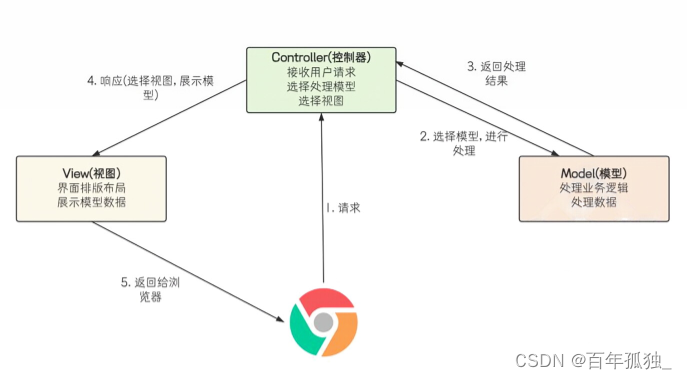
JAVA极简图书管理系统,初识springboot后端项目
前提条件: 具备基础的springboot 知识 Java基础 废话不多说! 创建项目 配置所需环境 将application.properties>application.yml 配置以下环境 数据库连接MySQL 自己创建的数据库名称为book_test server:port: 8080 spring:datasource:url:…...

MySQL 重新初始化实例
1、关闭mysql服务 service mysqld stop 2、清理datadir(本例中指定的是/var/lib/mysql)指定的目录下的文件,将该目录下的所有文件删除或移动至其他位置 cd /var/lib/mysql mv * /opt/mysql_back/ 3、初始化实例 /usr/local/mysql/bin/mysqld --initialize --u…...
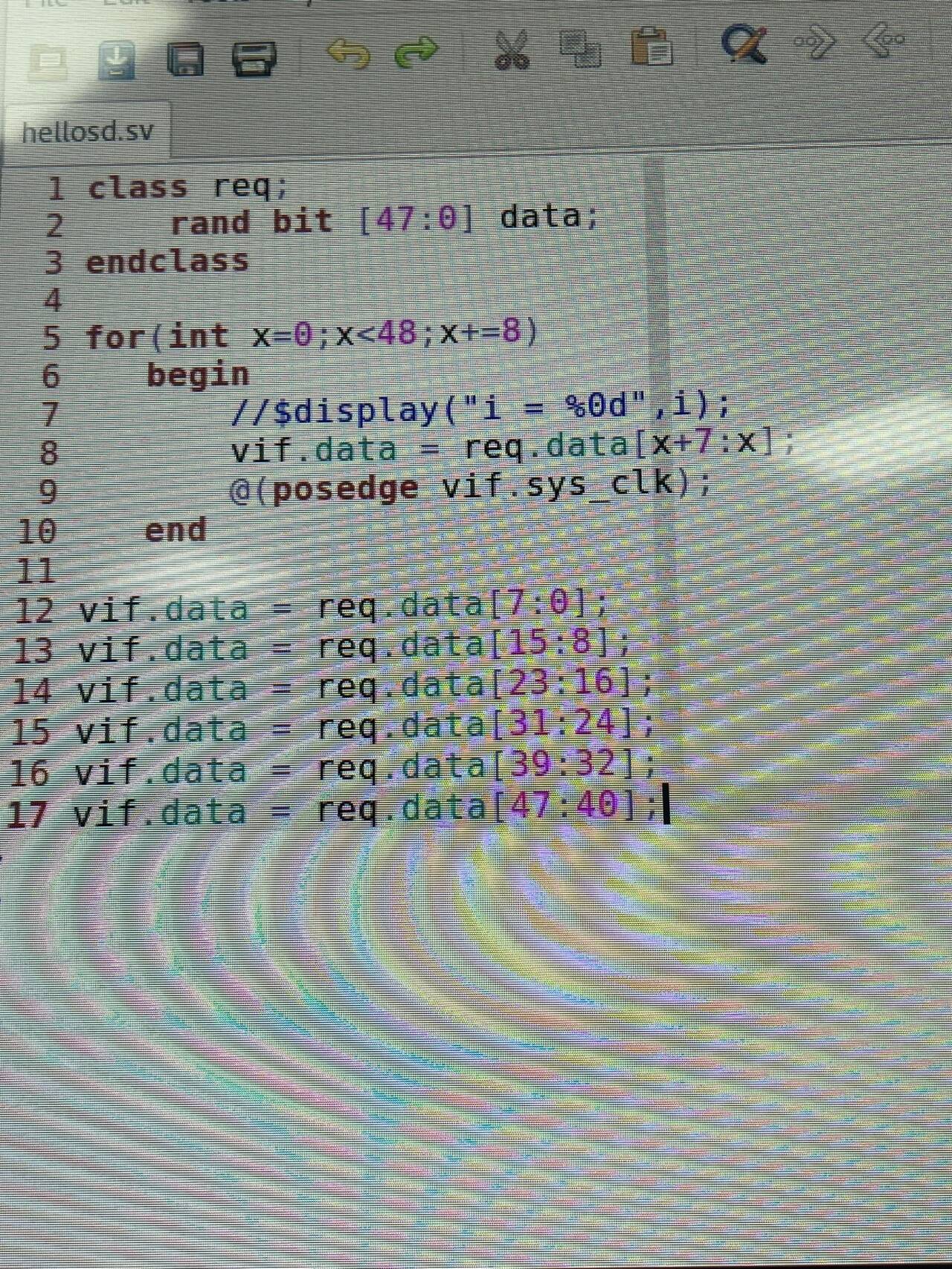
VCS编译bug汇总
‘typedef’ is not expected to be used in this contex 注册前少了分号。 Scope resolution error resolution : 声明指针时 不能与类名同名,即 不能声明为adapter. cannot find member "type_id" 忘记注册了 拼接运算符使用 关键要加上1b࿰…...
?)
【2024LLM应用-数据预处理】之如何从PDF,PPT等非结构化数据提取有效信息(结构化数据JSON)?
🥰大家知道吗,之前在给AI大模型"喂数据"的时候,我们往往需要把非结构化数据(比如PDF、PPT、Excel等)自己手动转成结构化的格式,这可真是太累人儿了。🥵 幸好现在有了Unstructured这个神级库,它内置的数据提取函数可以帮我们快速高效地完成这个…...

冯雷老师:618大退货事件分析
近日冯雷老师受邀为某头部电商36名高管进行培训,其中聊到了今年618退货潮的问题。以下内容整理自冯雷老师的部分授课内容。 一、引言 随着电子商务的蓬勃发展,每年的618大促已成为消费者和商家共同关注的焦点。然而,在销售额不断攀升的同时…...

JAVA基础教程DAY0-基础知识
JAVA语言的特点 简单性、面向对象、安全性、跨平台性、支持多线程、分布性 面向对象编程(Object-Oriented Programming,简称OOP)是一种编程范式,它通过将数据和操作这些数据的方法封装在一起,以创建对象的形式来组织代…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
