【C++进阶学习】第五弹——二叉搜索树——二叉树进阶及set和map的铺垫
二叉树1:深入理解数据结构第一弹——二叉树(1)——堆-CSDN博客
二叉树2:深入理解数据结构第三弹——二叉树(3)——二叉树的基本结构与操作-CSDN博客
二叉树3:深入理解数据结构第三弹——二叉树(3)——二叉树的基本结构与操作-CSDN博客
前言:
在之前我们用C语言实现数据结构时,已经对二叉树进行了系统的学习,但还是有一些内容并没有涉及到,比如今天要讲的二叉搜索树,因为二叉搜索树在C++中有现成的模板库——set和map,并且实现起来较为麻烦,所以我们放到这里来讲,对前面二叉树部分有所遗忘的同学可以在我的主页搜一下之前的文章看一下
目录
一、二叉搜索树的概念
二、二叉搜索树的基本操作
1. 插入节点
2. 查找节点
3. 删除节点
三、二叉搜索树的实现
四、二叉搜索树的应用
五、总结
一、二叉搜索树的概念
二叉搜索树又称二叉排序树,它是一种具有特殊性质的二叉树,它具有以下特点:
1. 有序性:对于树中的每个节点,其左子树中的所有节点的值都小于该节点的值,而其右子树中的所有节点的值都大于该节点的值。
2. 唯一性:树中的每个节点的值都是唯一的,不存在重复的值。
3. 递归性:它的子树也都是二叉树
上面这三种性质,最不好理解的应该是有序性,下面我们通过两个例子来展现这三种性质:
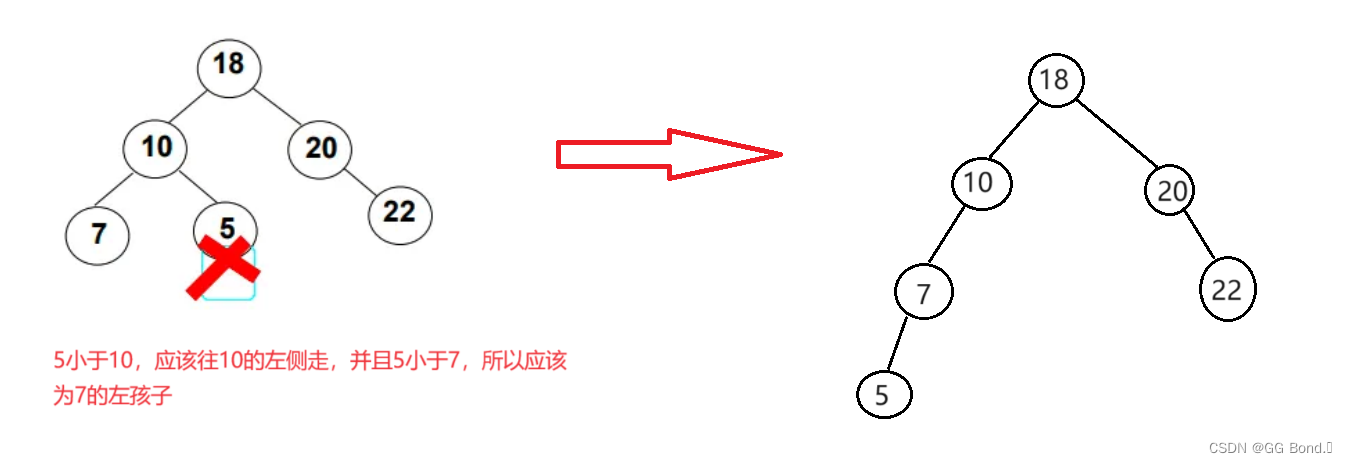
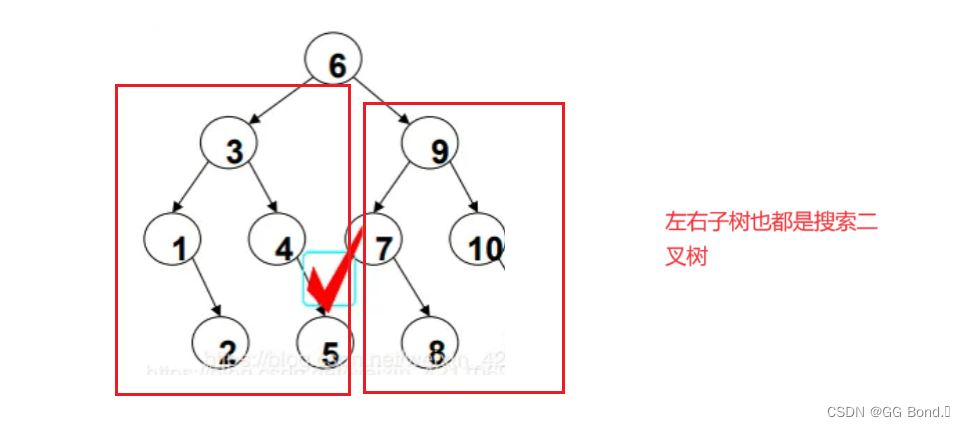
二、二叉搜索树的基本操作
1. 插入节点
插入节点的过程如下:
- 从根节点开始,比较要插入的值与当前节点的值。
- 如果要插入的值小于当前节点的值,则移动到左子节点;如果要插入的值大于当前节点的值,则移动到右子节点。
- 重复上述过程,直到找到一个空位置,然后在该位置插入新节点。
2. 查找节点
查找节点的过程如下:
- 从根节点开始,比较要查找的值与当前节点的值。
- 如果要查找的值等于当前节点的值,则返回该节点。
- 如果要查找的值小于当前节点的值,则移动到左子节点;如果要查找的值大于当前节点的值,则移动到右子节点。
- 重复上述过程,直到找到目标节点或遍历到空节点。
3. 删除节点
删除节点的过程相对复杂,需要考虑以下几种情况:
- 删除叶子节点:直接删除该节点。
- 删除只有一个子节点的节点:将其子节点替换到该节点的位置。
- 删除有两个子节点的节点:找到该节点右子树中的最小节点(或左子树中的最大节点),将其值替换到该节点的位置,然后删除该最小节点。
三、二叉搜索树的实现
template<class T>
struct BSTNode
{BSTNode(const T& data = T()): _pLeft(nullptr) , _pRight(nullptr), _data(data){}BSTNode<T>* _pLeft;BSTNode<T>* _pRight;T _data;
};
template<class T>
class BSTree
{typedef BSTNode<T> Node;typedef Node* PNode;
public:BSTree(): _pRoot(nullptr){}// 自己实现,与二叉树的销毁类似~BSTree();// 根据二叉搜索树的性质查找:找到值为data的节点在二叉搜索树中的位置PNode Find(const T& data);bool Insert(const T& data){// 如果树为空,直接插入if (nullptr == _pRoot){_pRoot = new Node(data);return true;}// 按照二叉搜索树的性质查找data在树中的插入位置PNode pCur = _pRoot;// 记录pCur的双亲,因为新元素最终插入在pCur双亲左右孩子的位置PNode pParent = nullptr;while (pCur){pParent = pCur;if (data < pCur->_data)
比特就业课pCur = pCur->_pLeft;else if (data > pCur->_data)pCur = pCur->_pRight; // 元素已经在树中存在elsereturn false;}// 插入元素pCur = new Node(data);if (data < pParent->_data)pParent->_pLeft = pCur;elsepParent->_pRight = pCur;return true;}bool Erase(const T& data){// 如果树为空,删除失败if (nullptr == _pRoot)return false;// 查找在data在树中的位置PNode pCur = _pRoot;PNode pParent = nullptr;while (pCur){if (data == pCur->_data)break;else if (data < pCur->_data){pParent = pCur;pCur = pCur->_pLeft;}else{pParent = pCur;pCur = pCur->_pRight;}}// data不在二叉搜索树中,无法删除if (nullptr == pCur)return false;// 分以下情况进行删除,同学们自己画图分析完成if (nullptr == pCur->_pRight){// 当前节点只有左孩子或者左孩子为空---可直接删除}else if (nullptr == pCur->_pRight){// 当前节点只有右孩子---可直接删除}else{
// 当前节点左右孩子都存在,直接删除不好删除,可以在其子树中找一个替代结点,
比如:// 找其左子树中的最大节点,即左子树中最右侧的节点,或者在其右子树中最小的节
点,即右子树中最小的节点// 替代节点找到后,将替代节点中的值交给待删除节点,转换成删除替代节点}return true;}
// 自己实现void InOrder();
private:PNode _pRoot;
};四、二叉搜索树的应用
在我们目前的学习中,二叉搜索树最重要的用途就是key--val模型,KV模型就是每一个key值都对应一个val值,这样就形成一个<key,val>键值对,这样的应用在生活中是非常常见的
比如:在菜市场中不同的蔬菜对应着不同的价格;新华词典中,不同的汉字对应着不同的拼音,这些都可以用KV模型来解决
下面是KV模型的实现(没有主函数):
namespace kv
{template<class K,class V>struct BSTreeNode{BSTreeNode<K,V>* _left;BSTreeNode<K,V>* _right;K _key;V _value;BSTreeNode(const K& key,const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K,class V>class BSTree{typedef BSTreeNode<K,V> Node;public://遍历(中序)void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}void InOrder(){_InOrder(_root);cout << endl;}///bool Insert(const K& key,const V& value){if (_root == nullptr){_root = new Node(key,value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return false;}}cur = new Node(key,value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 准备删除 20:15继续if (cur->_left == nullptr){//左为空if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr){//右为空if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{//左右都不为空// 右树的最小节点(最左节点)Node* parent = cur;Node* subLeft = cur->_right;while (subLeft->_left){parent = subLeft;subLeft = subLeft->_left;}swap(cur->_key, subLeft->_key);if (subLeft == parent->_left)parent->_left = subLeft->_right;elseparent->_right = subLeft->_right;delete subLeft;}return true;}}return false;}BSTree() = default;~BSTree(){Destroy(_root);}//递归版本bool InsertR(const K& key){return _InsertR(_root, key);}bool FindR(const K& key){return _FindR(_root, key);}bool EraseR(const K& key){return _EraseR(_root, key);}BSTree(const BSTree<K,V>& t){_root = Copy(t._root);}BSTree<K,V>& operator=(BSTree<K,V> t){swap(_root, t._root);return *this;}private:Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newroot = new Node(root->_key);newroot->_left = Copy(root->_left);newroot->_right = Copy(root->_right);return newroot;}void Destroy(Node*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}bool _EraseR(Node*& root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{if (root->_left == nullptr){root = root->_right;return true;}else if (root->_right == nullptr){root = root->_left;return true;}else{Node* subLeft = root->_right;while (subLeft->_left){subLeft = subLeft->_left;}swap(root->_key, subLeft->_key);return _EraseR(root->_right, key);}}}bool _FindR(Node* root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return root->_right;}else if (root->_key > key){return root->_left;}else{return true;}}bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key < key){return _InsertR(root->_right, key);}else if (root->_key > key){return _InsertR(root->_left, key);}else{return false;}}Node* _root = nullptr;};
}
五、总结
以上就是二叉搜索树的主要内容,在代码实现上其实与之前讲的二叉树差别并不是很大,关键在于思路的梳理,这章就先到这了

感谢各位大佬观看,创作不易,还请各位大佬点赞支持!!!
相关文章:

【C++进阶学习】第五弹——二叉搜索树——二叉树进阶及set和map的铺垫
二叉树1:深入理解数据结构第一弹——二叉树(1)——堆-CSDN博客 二叉树2:深入理解数据结构第三弹——二叉树(3)——二叉树的基本结构与操作-CSDN博客 二叉树3:深入理解数据结构第三弹——二叉树…...
【RabbitMQ实战】Springboot 整合RabbitMQ组件,多种编码示例,带你实践 看完这一篇就够了
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、对RabbitMQ管理界面深入了解1、在这个界面里面我们可以做些什么? 二、编码练习(1)使用direct exchange(直连型交换机)&a…...

【你也能从零基础学会网站开发】理解DBMS数据库管理系统架构,从用户到数据到底经历了什么
🚀 个人主页 极客小俊 ✍🏻 作者简介:程序猿、设计师、技术分享 🐋 希望大家多多支持, 我们一起学习和进步! 🏅 欢迎评论 ❤️点赞💬评论 📂收藏 📂加关注 其实前面我们也…...

Vue.js 中的API接口封装实战与详解
在开发Web应用的过程中,我们常常需要和服务器进行数据交互,这就涉及到了API接口的调用。在Vue.js项目中,为了提高代码复用性、可维护性和降低错误率,我们将API接口进行合理的封装显得尤为重要。本文将详细介绍如何在Vue.js项目中实…...

职场内卷、不稳定、没前景……怎么破?
经济下行期,大家普遍反映混职场艰难。 再深究下,发现造成职场艰难的原因主要有三个: 1.内卷:狼多肉少 2.不稳定:裁员总是不期而遇 3.没前景:明知过几年会被优化,但无法改变,死气沉沉…...
LeetCode 算法:将有序数组转换为二叉搜索树 c++
原题链接🔗:将有序数组转换为二叉搜索树 难度:简单⭐️ 题目 给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡 二叉搜索树。 示例 1: 输入:nums [-10,-3,0,5,9]…...
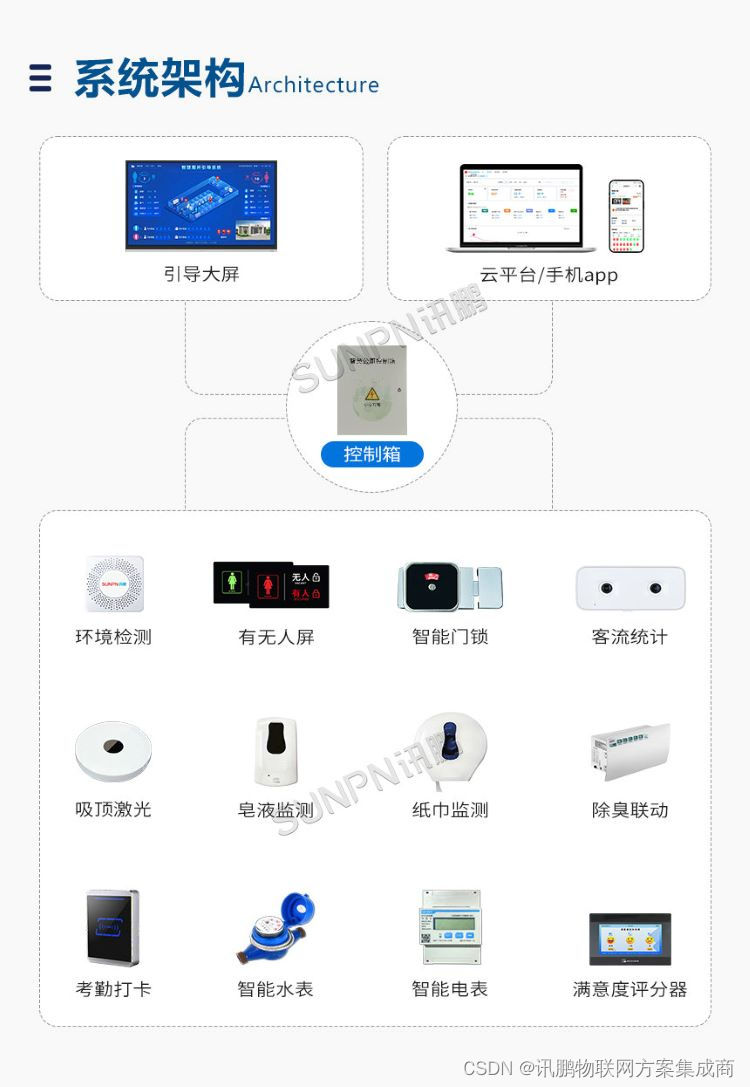
智慧公厕系统改变了人们对服务区公厕的看法
在过去,服务区公厕常常给人留下脏乱差的印象,成为人们在长途旅行途中不愿停留的地方。然而,随着智慧科技的不断发展和应用,智慧公厕系统的出现改变了人们对服务区公厕的看法,为公共卫生设施的提升注入了新的活力。 一、…...

终极指南:RNNS、Transformers 和 Diffusion 模型
一、说明 作为广泛使用这些工具和模型的人,我的目标是解开 RNN、Transformer 和 Diffusion 模型的复杂性和细微差别,为您提供详细的比较,为您的特定需求提供正确的选择。 无论您是在构建语言翻译系统、生成高保真图像,还是处理时间…...

WPF UI 3D 基本概念 点线三角面 相机对象 材质对象与贴图 3D地球 光源 变形处理 动作交互 辅助交互插件 系列三
WPF UI交互专题 平面图形 Path Drawing 绘图 渐变 Brush 矩阵 Transform 变形 阴影效果 模糊效果 自定义灰度去色效果 系列二-CSDN博客 1软件中的3D基本概念 WPF 中 3D 功能的设计初衷并非提供功能齐全的游戏开发平台。 WPF 中的 3D 图形内容封装在 Viewport3D 元素中&#x…...
分子AI预测赛Task2笔记
下面所述比较官方的内容都来自官方文档 Task2:赛题深入解析 - 飞书云文档 (feishu.cn) 赛题背景 强调了人工智能在科研领域&…...

剖析DeFi交易产品之UniswapV4:创建池子
本文首发于公众号:Keegan小钢 创建池子的底层函数是 PoolManager 合约的 initialize 函数,其代码实现并不复杂,如下所示: function initialize(PoolKey memory key, uint160 sqrtPriceX96, bytes calldata hookData)externalover…...

速盾:cdn内容分发服务有哪些优势?
CDN(Content Delivery Network)是指内容分发网络,是一种将网络内容分发到全球各个地点的技术和架构。在现代互联网架构中,CDN已经变得非常重要。CDN通过将内容分发到靠近用户的服务器上,提供高速、高效的服务。下面是C…...

如何利用React和Python构建强大的网络爬虫应用
如何利用React和Python构建强大的网络爬虫应用 引言: 网络爬虫是一种自动化程序,用于通过互联网抓取网页数据。随着互联网的不断发展和数据的爆炸式增长,网络爬虫越来越受欢迎。本文将介绍如何利用React和Python这两种流行的技术,…...

炎黄数智人:招商局集团推出AI数字员工“招小影”
引言 在全球数字化浪潮的推动下,招商局集团开启了一项具有里程碑意义的项目。招商局集团将引入AI数字员工“招小影”,这一举措不仅彰显了招商局集团在智能化转型方面的坚定决心,也为企业管理模式的创新注入了新的活力。 “招小影”是一款集成…...
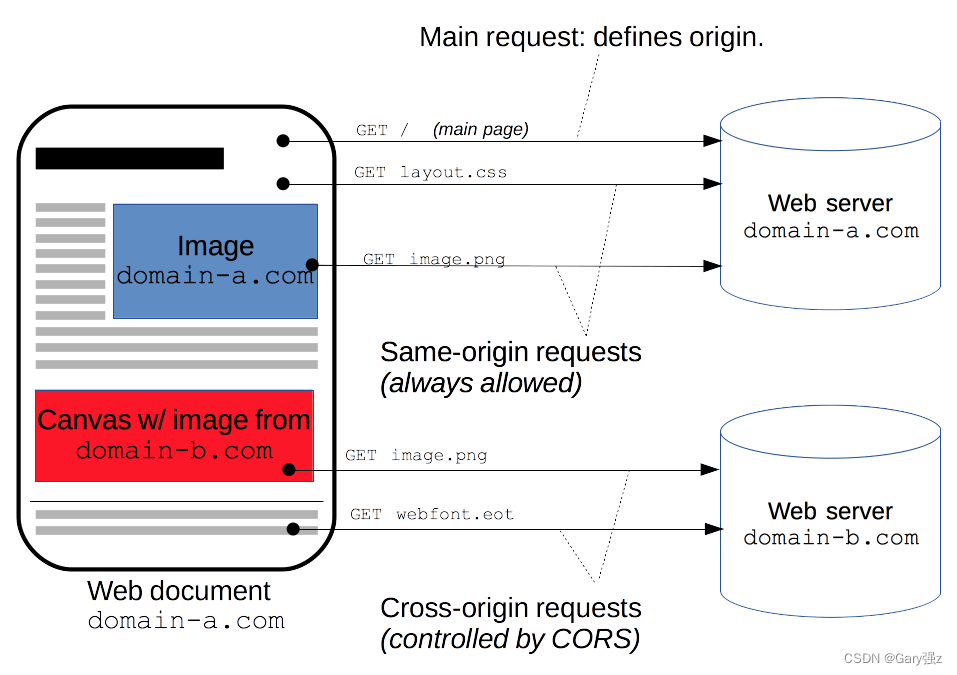
【开发篇】明明配置跨域声明,为什么却仍可以发送HTTP请求
一、问题 在SpringBoot项目中,明确指定仅允许指定网站跨域访问: 为什么开发人员却仍旧可以通过HTTP工具调用接口? 二、为什么 在回答这个问题之前,我们首先要了解一下什么是CORS! 1、什么是CORS CORS的全称为跨域资源…...
单片机中有FLASH为啥还需要EEROM?
在开始前刚好我有一些资料,是我根据网友给的问题精心整理了一份「单片机的资料从专业入门到高级教程」, 点个关注在评论区回复“888”之后私信回复“888”,全部无偿共享给大家!!! 一是EEPROM操作简单&…...
)
Qt的源码目录集合(V5.12.12版本)
目录 1.QObject实现源码 2.qml中的ListModel实现源码 3.qml中的JS运行时的环境和数据类型源码 1.QObject实现源码 .\Qt\Qt5.12.12\5.12.12\Src\qtbase\src\corelib\kernel\qobject.h .\Qt\Qt5.12.12\5.12.12\Src\qtbase\src\corelib\kernel\qobject.cpp .\Qt\Qt5.12.12\5…...
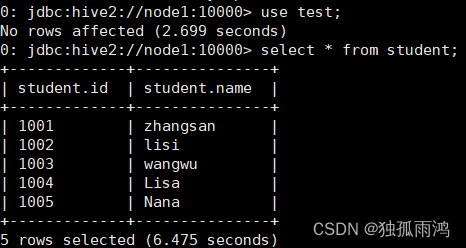
记因hive配置文件参数运用不当导致 sqoop MySQL导入数据到hive 失败的案例
sqoop MySQL导入数据到hive报错 ERROR tool.ImportTool: Encountered IOException running import job: java.io.IOException: Hive exited with status 64 报错解释: 这个错误表明Sqoop在尝试导入数据到Hive时遇到了问题,导致Hive进程异常退出。状态码…...

自动化邮件通知:批处理脚本的通讯增强
自动化邮件通知:批处理脚本的通讯增强 引言 批处理脚本在自动化任务中扮演着重要角色,无论是在系统管理、数据处理还是日常任务调度中。然而,批处理脚本的自动化能力可以通过集成邮件通知功能得到显著增强。当脚本执行完毕或在执行过程中遇…...
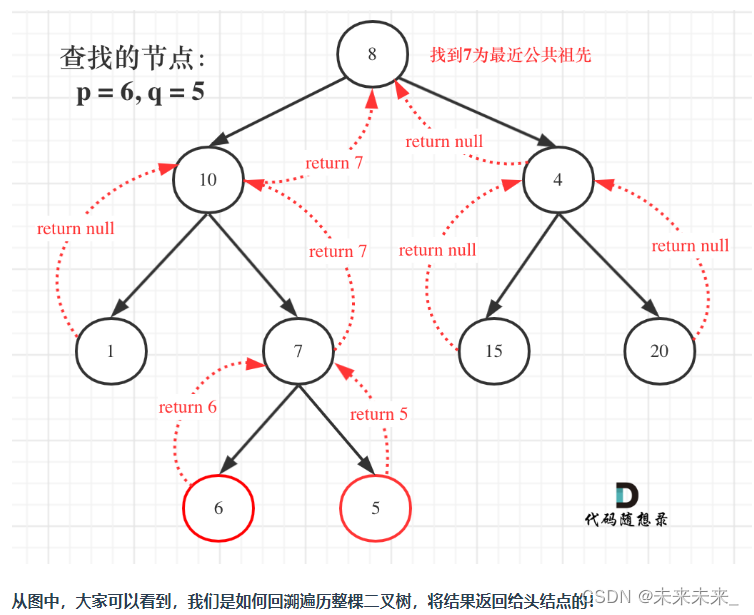
236、二叉树的最近公共祖先
前提: 所有 Node.val 互不相同 。p ! qp 和 q 均存在于给定的二叉树中。 代码如下: class Solution { public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if (root q || root p || root NULL) return root;TreeN…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
