Java加解密(八)工具篇
目录
- Java加解密实用工具
- 1 OpenSSL
- 2 Keytool
- 3 XCA
- 4 KeyStore Explorer
Java加解密实用工具
1 OpenSSL
OpenSSL是一个开放源代码的软件库包,应用程序可以使用这个包来进行安全通信,避免窃听,同时确认另一端连接者的身份。
例如Apache 使用它加密 HTTPS,OpenSSH 使用它加密 SSH。
OpenSSL整个软件包大概可以分成三个主要的功能部分:
- SSL协议库
OpenSSL实现了SSL协议的SSLv2和SSLv3,支持了其中绝大部分算法协议。OpenSSL也实现了TLSv1.0,TLS是SSLv3的标准化版,虽然区别不大,但毕竟有很多细节不尽相同。
虽然已经有众多的软件实现了OpenSSL的功能,但是OpenSSL里面实现的SSL协议能够让我们对SSL协议有一个更加清楚的认识,因为至少存在两点:一是OpenSSL实现的SSL协议是开放源代码的,我们可以追究SSL协议实现的每一个细节;二是OpenSSL实现的SSL协议是纯粹的SSL协议,没有跟其它协议(如HTTP)协议结合在一起,澄清了SSL协议的本来面目。 - 应用程序
- 密钥证书管理
密钥和证书管理是PKI的一个重要组成部分,OpenSSL为之提供了丰富的功能,支持多种标准。
首先,OpenSSL实现了ASN.1的证书和密钥相关标准,提供了对证书、公钥、私钥、证书请求以及CRL等数据对象的DER、PEM和BASE64的编解码功能。OpenSSL提供了产生各种公开密钥对和对称密钥的方法、函数和应用程序,同时提供了对公钥和私钥的DER编解码功能。并实现了私钥的PKCS#12和PKCS#8的编解码功能。OpenSSL在标准中提供了对私钥的加密保护功能,使得密钥可以安全地进行存储和分发。
在此基础上,OpenSSL实现了对证书的X.509标准编解码、PKCS#12格式的编解码以及PKCS#7的编解码功能。并提供了一种文本数据库,支持证书的管理功能,包括证书密钥产生、请求产生、证书签发、吊销和验证等功能。
事实上,OpenSSL提供的CA应用程序就是一个小型的证书管理中心(CA),实现了证书签发的整个流程和证书管理的大部分机制。 - OpenSSL对于随机数的生成和管理也提供了一整套的解决方法和支持API函数。随机数的好坏是决定一个密钥是否安全的重要前提。
- 密钥证书管理
- 密码算法库
- 对称加密
OpenSSL一共提供了8种对称加密算法,其中7种是分组加密算法,仅有的一种流加密算法是RC4。这7种分组加密算法分别是AES、DES、Blowfish、CAST、IDEA、RC2、RC5,都支持电子密码本模式(ECB)、加密分组链接模式(CBC)、加密反馈模式(CFB)和输出反馈模式(OFB)四种常用的分组密码加密模式。其中,AES使用的加密反馈模式(CFB)和输出反馈模式(OFB)分组长度是128位,其它算法使用的则是64位。事实上,DES算法里面不仅仅是常用的DES算法,还支持三个密钥和两个密钥3DES算法。 - 非对称加密
OpenSSL一共实现了4种非对称加密算法,包括DH算法、RSA算法、DSA算法和椭圆曲线算法(EC)。DH算法一般用于密钥交换。RSA算法既可以用于密钥交换,也可以用于数字签名,当然,如果你能够忍受其缓慢的速度,那么也可以用于数据加密。DSA算法则一般只用于数字签名。 - 信息摘要
OpenSSL实现了5种信息摘要算法,分别是MD2、MD5、MDC2、SHA(SHA1)和RIPEMD。SHA算法事实上包括了SHA和SHA1两种信息摘要算法。此外,OpenSSL还实现了DSS标准中规定的两种信息摘要算法DSS和DSS1。
- 对称加密
OpenSSL 包含一个命令行工具用来完成 OpenSSL 库中的所有功能,官网及下载地址:
https://www.openssl.org/
http://slproweb.com/products/Win32OpenSSL.html
2 Keytool
keytool 是JDK 提供的证书相关操作的命令行工具,只要安装JDK 并且配置好相应的环境变量或者切换工作目录至keytool工具目录下,就可以在命令窗口运行。
C:\Users\Administrator>keytool -help
密钥和证书管理工具命令:-certreq 生成证书请求-changealias 更改条目的别名-delete 删除条目-exportcert 导出证书-genkeypair 生成密钥对-genseckey 生成密钥-gencert 根据证书请求生成证书-importcert 导入证书或证书链-importpass 导入口令-importkeystore 从其他密钥库导入一个或所有条目-keypasswd 更改条目的密钥口令-list 列出密钥库中的条目-printcert 打印证书内容-printcertreq 打印证书请求的内容-printcrl 打印 CRL 文件的内容-storepasswd 更改密钥库的存储口令使用 "keytool -command_name -help" 获取 command_name 的用法C:\Users\Administrator>
C:\Users\Administrator>keytool -certreq -help
keytool -certreq [OPTION]...生成证书请求选项:-alias <alias> 要处理的条目的别名-sigalg <sigalg> 签名算法名称-file <filename> 输出文件名-keypass <arg> 密钥口令-keystore <keystore> 密钥库名称-dname <dname> 唯一判别名-storepass <arg> 密钥库口令-storetype <storetype> 密钥库类型-providername <providername> 提供方名称-providerclass <providerclass> 提供方类名-providerarg <arg> 提供方参数-providerpath <pathlist> 提供方类路径-v 详细输出-protected 通过受保护的机制的口令
C:\Users\Administrator>keytool -changealias -help
keytool -changealias [OPTION]...更改条目的别名选项:-alias <alias> 要处理的条目的别名
-destalias <destalias> 目标别名
-keypass <arg> 密钥口令
-keystore <keystore> 密钥库名称
-storepass <arg> 密钥库口令
-storetype <storetype> 密钥库类型
-providername <providername> 提供方名称
-providerclass <providerclass> 提供方类名
-providerarg <arg> 提供方参数
-providerpath <pathlist> 提供方类路径
-v 详细输出
-protected 通过受保护的机制的口令
3 XCA
XCA(X Certificate and key management) 是作为证书和密钥存储,以及作为签发证书的签名应用程序,是一个开源的工具,底层还是基于openssl的类库和API的。
首先需要下载并安装工具,官网地址为:https://www.hohnstaedt.de/xca/index.php/download

4 KeyStore Explorer
KeyStore Explorer KeyStoreExplorer是Java命令行程序keytool和jarsigner的开源GUI替代工具。KeyStore Explorer通过直观的图形用户界面展示其丰富的功能。
首先需要下载并安装工具,官网地址为:https://keystore-explorer.org/downloads.html


相关文章:

Java加解密(八)工具篇
目录Java加解密实用工具1 OpenSSL2 Keytool3 XCA4 KeyStore ExplorerJava加解密实用工具 1 OpenSSL OpenSSL是一个开放源代码的软件库包,应用程序可以使用这个包来进行安全通信,避免窃听,同时确认另一端连接者的身份。 例如Apache 使用它加…...

Go框架三件套(Web/RPC/ORM)
🧡 三件套介绍 Gorm Gorm 是一个已经迭代了10年的功能强大的 ORM 框架,在字节内部被广泛使用并且拥有非常丰富的开源扩展。 Kitex Kitex 是字节内部的 Golang 微服务 RPC 框架,具有高性能、强可扩展的主要特点,支持多协议并且拥有…...

HR问:假如公司给不到你期望的薪资怎么办?这个问题该如何体面地回答?
对大多数人而言,跳槽就是为了涨薪,工作就是为了挣钱。但如果面试时hr问:假如公司给不到你期望的薪资呢?面对这种问题,该怎么回答才体面?来看一波网友的机智回答:有人委婉拒绝,说“愿…...

LearnOpenGL-高级OpenGL-2.模板测试
本人刚学OpenGL不久且自学,文中定有代码、术语等错误,欢迎指正 我写的项目地址:https://github.com/liujianjie/LearnOpenGLProject 文章目录简单理解模板测试模板介绍模板函数物体轮廓介绍代码给加载的模型添加轮廓简单理解 同深度测试一样…...
【Git从入门到精通】Git入门
什么是版本控制 版本控制是一套系统,按时间记录某一个或一系列文件的变更,查看以前的特定版本。 使用版本控制系统,你可以将文件或者整个项目恢复到先前的状态,还可以对以前的文件进行对比。 本地版本控制系统 本地版本控制系…...

软件测试18
在桌面上打开终端窗口, 执行如下操作: 查看当前系统中开放的端口有哪些查看哪个程序正在使用 3306 端口(需要 root 用户权限) 注意: 1.某些端口号具备固定用途: 例如: 远程访问常用端口号:22 默认情况下是mysql使用的端口号&…...

C语言实现快速排序(hoare法、挖坑法、前后指针法与非递归实现)——不看后悔系列
目录 1. hoare法 方法与步骤 代码实现 2. 挖坑法 方法与步骤 代码实现 3. 前后指针法 方法与步骤 代码实现 4. 快速排序的缺点与优化 1.快速排序的缺点 2.快速排序的优化 ① 三数取中法选 key 代码实现 ② 小区间优化 代码实现 5. 快速排序的非递归实现 附录…...

如何为系统可靠性的量化提供依据
SLA 即 Service Level Agreement,也就是服务等级协议,它指的是系统服务提供者(Provider)对客户(Customer)的一个服务承诺。 而 SLO 就是 SLA 的具体目标管理办法,它由一系列相关的指标 SLI &am…...

量化投资中的因子是什么?因子是如何分类的,包括哪些?
因子就是对个股有解释的因素。因子的种类很多,不同类别的因子从不同的维度对个股收益进行解释。比如基本面因子的数据来源方面有很大一部分是财务报表,从估值、成长、盈利能力等多个方面对股票收益进行解释。量价因子是围绕价格、成交量等技术指标构建的…...

力扣-修复表中的名字
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:1667. 修复表中的名字二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其他…...

【博客633】linux vxlan设备工作原理
linux vxlan设备工作原理 vxlan处理包的原理:以k8s cni flannel组件创建的vxlan设备为例 1、k8s cni组件创建flannel设备flannel.1,且这个设备为vxlan类型的设备 root10.10.10.12:/home/ubuntu# ethtool -i flannel.1 driver: vxlan version: 0.1 fi…...

3.12学习周报
文章目录前言文献阅读摘要简介方法介绍讨论结论相关性分析总结前言 本周阅读文献《Streamflow and rainfall forecasting by two long short-term memory-based models》,文献主要提出两种基于长短时记忆网络的混合模型用于对水流量和降雨量进行预测。小波-LSTM&am…...
电力电子中逐波限流控制以及dsp实现
逐波限流是指在电力系统运行中,对电力设备进行电流保护的一种措施。它的实现方式是通过对电力系统的电流进行逐波监测和控制,每一波电流都可以独立地进行限制,从而保护电力系统设备不受过载损坏或短路故障的影响。 逐波限流的作用是提高电力…...
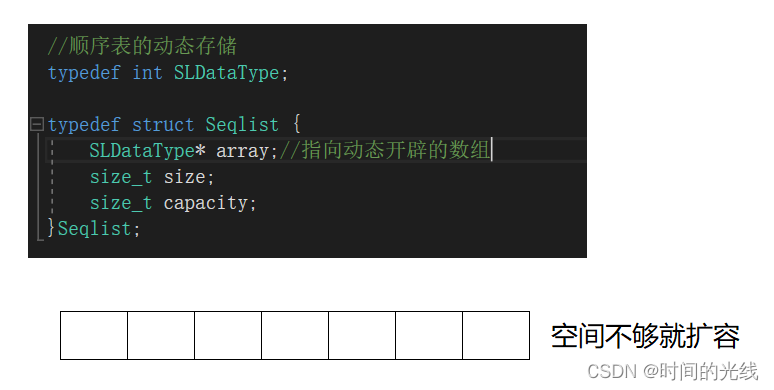
【数据结构】 顺序表
文章目录1 线性表2 顺序表2.1 概念及结构2.2 接口实现2.3 数组相关面试题2.4 顺序表的问题与思考1 线性表 线性表(linear list)是n个具有相同特性的数据元素的有限序列。线性表是一种在实际中广泛使用的数据结构,常见的线性表:顺序…...

Elasticsearch 集群规划- 单台机器核心数计算公式
在做集群规划的时候,到底需要给集群的每个节点多少个核心数?这个问题一直困扰了我很久。最近一段时间做千亿数据,PB存储量集群规划的时候,突然想明白了这件事,大致可以用一个公式来计算!我觉得这是一个非常…...

Tesla都使用什么编程语言?
作者 | 初光 出品 | 车端 备注 | 转载请阅读文中版权声明 知圈 | 进“汽车电子与AutoSAR开发”群,请加微“cloud2sunshine” 总目录链接>> AutoSAR入门和实战系列总目录 带着对更美好未来的愿景,特斯拉不仅成为有史以来最有价值的汽车公司&…...

1143. 最长公共子序列——【Leetcode每日刷题】
1143. 最长公共子序列 给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。 一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些…...
、obj.notify()、obj.notifyAll()详解)
【并发基础】线程的通知与等待:obj.wait()、obj.notify()、obj.notifyAll()详解
目录 〇、先总结一下这三个方法带来的Java线程状态变化 一、obj.wait() 1.1 作用 1.2 使用前需要持有线程共享对象的锁 1.3 使用技巧 二、obj.notify(All)() 1.1 notify() 方法 1.1.1 调用notify()或notifyAll()不会释放线程的锁 1.2 notifyAll() 方法 1.3 使用技巧 三、使用实…...

css黏性定位-实现商城的分类滚动的标题吸附
传统的黏性定位是使用js通过计算高度来实现的,当元素滚动到一定位置时吸附在当前位置。下面我们通过css来实现黏性定位功能。 黏性定位 黏性定位目前主流的浏览器已经全部支持,顾名思义,黏性定位具有吸附的效果,其实它是positio…...

@Component和@bean注解在容器中创建实例区别
Component和Bean的区别 在Spring Boot中,Component注解和Bean注解都可以用于创建bean。它们的主要区别在于它们的作用范围和创建方式。 Component注解是一种通用的注解,可以用于标注任何类。被标注的类将被Spring容器自动扫描并创建为一个bean。这个bea…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
