Matlab绘制隐函数总结-二维和三维
1.二维隐函数
二维隐函数满足f(x,y)=0f(x,y)=0f(x,y)=0,这里无法得到y=f(x)y=f(x)y=f(x)的形式。不能通过普通函数绘制。
我们要关注的是使用fplot函数和fimplicit函数。
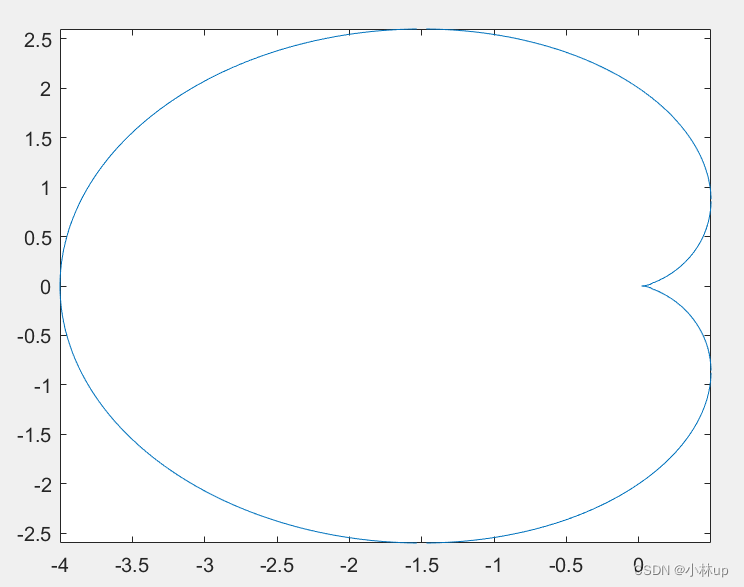
第1种情况:基本隐函数
基本的隐函数形式形如:
x2+y2+2x=2(x2+y2)12x^{2}+y^{2}+2 x=2\left(x^{2}\right.\left.+y^{2}\right)^{\frac{1}{2}}x2+y2+2x=2(x2+y2)21
原来有个ezplot函数的,但是现在Matlab不推荐使用了,可能要慢慢淘汰掉了。老版的写法是
ezplot('x^2+y^2+2*x=2*sqrt(x^2+y^2)')或者
syms x y ezplot(x^2+y^2+2*x-2*sqrt(x^2+y^2))(后面我们也不再谈ezplot函数)
下面是官方推荐的写法:
使用fplot函数
fplot('x^2+y^2+2*x=2*sqrt(x^2+y^2)')
使用fimplicit函数
注意和fplot函数不同,Matlab官方提示:为了获得最佳性能和避免产生警告消息,请使用按元素运算符。例如,使用 x.*y 而不是 x*y。
fimplicit( x.^2+y.^2+2.*x-2.*sqrt(x.^2+y.^2))
或者
fimplicit(@(x,y) x.^2+y.^2+2.*x-2.*sqrt(x.^2+y.^2))
总结:一般的隐函数可以使用fplot函数或者fimplicit函数绘制。
第2种情况:隐函数带变量
形如:
x2+y2+ax=a(x2+y2)12x^{2}+y^{2}+a x=a\left(x^{2}+y^{2}\right)^{\frac{1}{2}}x2+y2+ax=a(x2+y2)21
根据实际需要可将aaa事先具体赋值, 但使用中应注意,绘图语句不能简单采用前面基本格式的 形式 ,不能写作,会报错
a = 2;
fplot('x^2+y^2+a*x-a*sqrt(x^2+y^2)');
因为函数包括单引号时,相当于是符号表达式,变量a的值作为一个参数,不能传进函数,导致fplot()不能正常绘图。
使用fimplicit函数
fplot函数测试了不行,使用fimplicit函数下面的代码是可以的。
a=2;
syms x y
fimplicit(x.^2+y.^2+ a.*x-a.*sqrt(x.^2+y.^2))
总结:带有未知参数的隐函数使用fimplicit函数绘制
第3种情况:带有多个变量的隐函数组的绘图
形如:
f(x,y)=x+y2=a,g(x,y)=x2−y=bf(x, y)=x+y^2=a,\quad g(x, y)=x^2-y=bf(x,y)=x+y2=a,g(x,y)=x2−y=b
不妨令:
a=3,b=−3a=3,b=-3a=3,b=−3
使用fimplicit函数
因为还是带有未知参数的隐函数,我们还是用使用fimplicit函数绘制。
a=3;b=-3;
syms x y
f=x+y^2-a;
g=x^2-y-b;
fimplicit(f);
hold on;
fimplicit(g)
title('x+y^2-a=0 x^2-y-b=0 a=3 b=-3')
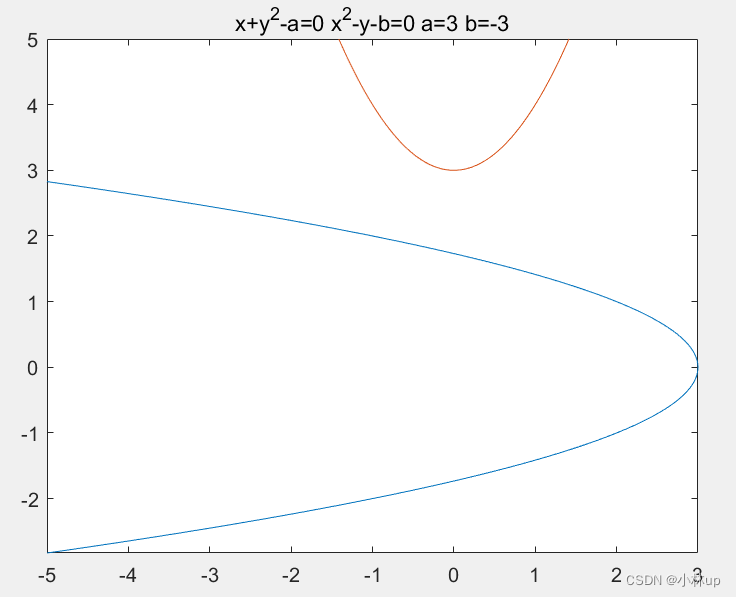
总结:带有多个变量的隐函数组使用fimplicit函数绘制,加上
hold on命令
2.三维隐函数
三维隐函数满足f(x,y,z)=0f(x,y,z)=0f(x,y,z)=0,这里无法得到z=f(x,y)z=f(x,y)z=f(x,y)的形式。不能通过普通函数绘制。
我们要关注的是使用等面值计算函数isosurface和面元渲染函数patch分布实现三维隐函数曲面的绘制方法。
我们使用isosurface的调用方式是
[f,v] = isosurface(X,Y,Z,V,isovalue)
官方的解释是该语句返回由isovalue指定的某个等值面的表面(Faces)和顶点(Vertices)数据,并存放在单独的数组f、v中。我们绘制的是v=f(x,y,z)=0v=f(x,y,z)=0v=f(x,y,z)=0的三维图形,则isovalue=0。
patch函数是面元渲染函数,对曲面进行修饰,相关的调用方式是:patch(X,Y,Z,C)
patch(X,Y,Z,C)
它以三维坐标(X,Y,Z)为顶点,构造三维曲面,c是R G B颜色向量。另一个相关的调用方式是:
patch('Faces',F,'Vertices',V)
它通过包含Faces、Vertices两个的数组F、V来构造三维曲面,F和V可以由等值面函数isosurface计算而得。
对于三元显函数v=f(x,y,z)v=f(x,y,z)v=f(x,y,z) 来说,当v=0v=0v=0时的等值面就是z=g(x,y)z=g(x,y)z=g(x,y)的三维曲面。isosurface函数可以计算v=0v=0v=0的等值面,返回结果包括表面和顶点数据,并存放于数组fff、vvv中,再输入给patch函数,能构造三维曲面,还可以根据需要设置颜色、亮度、三维视角等。画图的步骤可以归纳为:
(1)用meshgrid函数产生网格点,同时可确定坐标范围。
(2)引用隐函数表达式计算格点函数值val。
(3)调用[f,v]=isosurface(x,y,z,val,0)计算隐函数等值面并返回到f、v。
(4)调用patch(‘Faces’,f,‘Vertices’,v,‘facecolor’,‘interp’,‘EdgeColor’,‘k’)对曲面修饰。
[x,y,z]=meshgrid(-1.5:0.1:1.5,-1.5:0.1:1.5,-1.5:0.1:1.5);
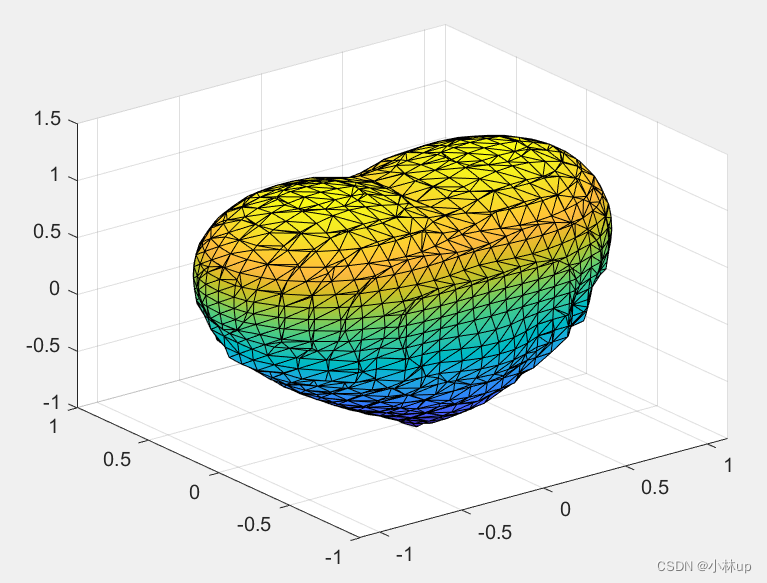
v=(x.^2+(9/4)*y.^2+z.^2-1).^3-x.^2.*z.^3-(9/80)*y.^2.*z.^3;
[f,v]=isosurface(x,y,z,v,0);
p=patch('Faces',f,'Vertices',v,'CData',v(:,3),'facecolor','interp',...'EdgeColor','k');
view(3); grid on;
来看下效果!
相关文章:

Matlab绘制隐函数总结-二维和三维
1.二维隐函数 二维隐函数满足f(x,y)0f(x,y)0f(x,y)0,这里无法得到yf(x)yf(x)yf(x)的形式。不能通过普通函数绘制。 我们要关注的是使用fplot函数和fimplicit函数。 第1种情况:基本隐函数 基本的隐函数形式形如: x2y22x2(x2y2)12x^{2}y^{…...

如何直观地理解傅立叶变换?频域和时域的理解
如何直观地理解傅立叶变换 傅里叶变换连续形式的傅立叶变换如何直观地理解傅立叶变换?一、傅里叶级数1.1傅里叶级数的三角形式1.2 傅里叶级数的复指数形式二、傅里叶变换2.1一维连续傅里叶变换三、频谱和功率谱3.1频谱的获得3.2频谱图的特征3.3频谱图的组成频域(frequency do…...
STC15读取内部ID示例程序
STC15读取内部ID示例程序🎉本案例基于STC15F2K60S2为验证对象。 📑STC15 ID序列介绍 STC15系列STC最新一代STC15系列单片机出厂时都具有全球唯一身份证号码(ID号)。最新STC15系列单片机的程序存储器的最后7个字节单元的值是全球唯一ID号,用…...
Xml格式化与高亮显示
具体请参考:Xml格式化与高亮显示...

【GlobalMapper精品教程】045:空间分析工具(2)——相交
GlobalMapper提供的空间分析(操作)的方法有:交集、并集、单并集、差异、对称差集、相交、重叠、接触、包含、等于、内部、分离等,本文主要讲述相交工具的使用。 文章目录 一、实验数据二、符号化设置三、相交运算四、结果展示五、心灵感悟一、实验数据 加载配套实验数据(…...
4年外包终上岸,我只能说这类公司能不去就不去..
我大学学的是计算机专业,毕业的时候,对于找工作比较迷茫,也不知道当时怎么想的,一头就扎进了一家外包公司,一干就是4年。现在终于跳槽到了互联网公司了,我想说的是,但凡有点机会,千万…...
sklearn降维算法1 - 降维思想与PCA实现
目录1、概述1.1 维度概念2、PCA与SVD2.1 降维实现2.2 重要参数n_components2.2.1 案例:高维数据的可视化2.2.2 最大似然估计自选超参数2.2.3 按信息量占比选超参数1、概述 1.1 维度概念 shape返回的结果,几维几个方括号嵌套 特征矩阵特指二维的 一般来…...

「期末复习」线性代数
第一章 行列式 行列式是一个数,是一个结果三阶行列式的计算:主对角线的乘积全排列与对换逆序数为奇就为奇排列,逆序数为偶就为偶排列对换:定理一:一个排列的任意两个元素对换,排列改变奇偶性(和…...
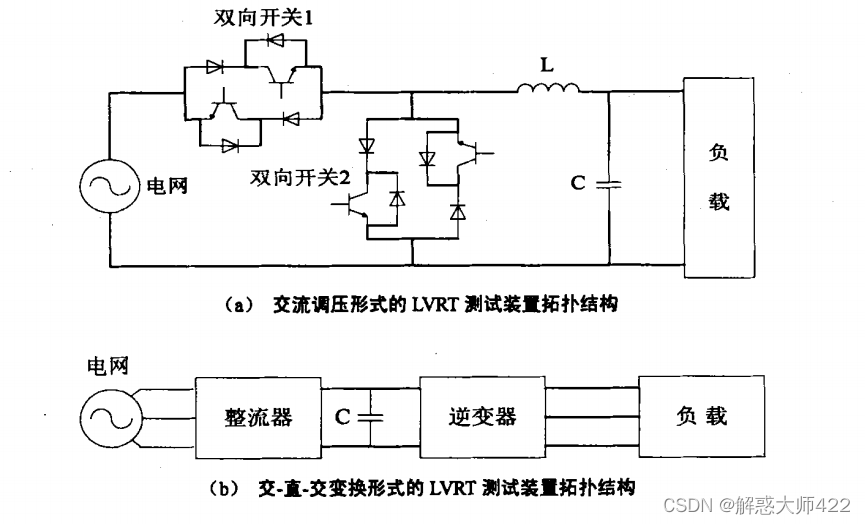
伏并网低电压穿越技术
国内光伏并网低电压穿越要求 略: 低电压穿越方法 当前,光伏电站实现低电压穿越可通过两种方式,即增加硬件设备或者改变控制策略。本节对基于储能设备、基于无功补偿设备、基于无功电流电压支撑控制策略三种实现LVRT的典型方法进行介绍。 …...
opencv的环境搭建
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…...

C++智能指针
c11的三个智能指针 unique_ptr独占指针,用的最多 shared_ptr记数指针,其次 weak_ptr,shared_ptr的补充,很少用 引用他们要加上头文件#include unique_ptr独占指针: 1.只能有一个智能指针管理内存 2.当指针超出作用域…...
MongoDB--》MongoDB数据库以及可视化工具的安装与使用—保姆级教程
目录 数据库简介 MongoDB数据库的安装 MongoDB数据库的启动 MongoDB数据库环境变量的配置 MongoDB图形化管理工具 数据库简介 在使用MongoDB数据库之前,我们应该要知道我们使用它的原因: 在数据库当中,有常见的三高需求: Hi…...

JAVA 基础题
1. 面向对象有哪些特征?答:继承、封装、多态2. JDK与JRE的区别是什么?答:JDK是java开发时所需环境,它包含了Java开发时需要用到的API,JRE是Java的运行时环境,JDK包含了JRE,他们是包含…...

Flutter desktop端多屏幕展示问题处理
目前越来越多的人用Flutter来做桌面程序的开发,很多应用场景在Flutter开发端还不是很成熟,有些场景目前还没有很好的插件来支持,所以落地Flutter桌面版还是要慎重。 下面来说一下近期我遇到的一个问题,之前遇到一个需要双屏展示的…...

每天10个前端小知识 【Day 9】
👩 个人主页:不爱吃糖的程序媛 🙋♂️ 作者简介:前端领域新星创作者、CSDN内容合伙人,专注于前端各领域技术,成长的路上共同学习共同进步,一起加油呀! ✨系列专栏:前端…...

Elasticsearch的读写搜索过程
问题 Elasticsearch在读写数据的过程是什么样的?你该如何理解这个问题! Elasticsearch的写数据过程 客户端选择一个节点发送请求,这个时候我们所说的这个节点就是协调节点(coordinating node)协调节点对document进行了路由&am…...

线上服务质量的问题该如何去处理?你有什么思路?
线上服务质量的问题该如何去处理?你有什么思路? 目录:导读 发现线上故障 处理线上故障 修复线上故障 运营线上质量 就是前几天有个同学问了我一个问题:目前业内高可用部署主要采用方案? 看到这个问题,…...

IOC 配置,依赖注入的三种方式
xml 配置 顾名思义,就是将bean的信息配置.xml文件里,通过Spring加载文件为我们创建bean。这种方式出现很多早前的SSM项目中,将第三方类库或者一些配置工具类都以这种方式进行配置,主要原因是由于第三方类不支持Spring注解。 优点…...
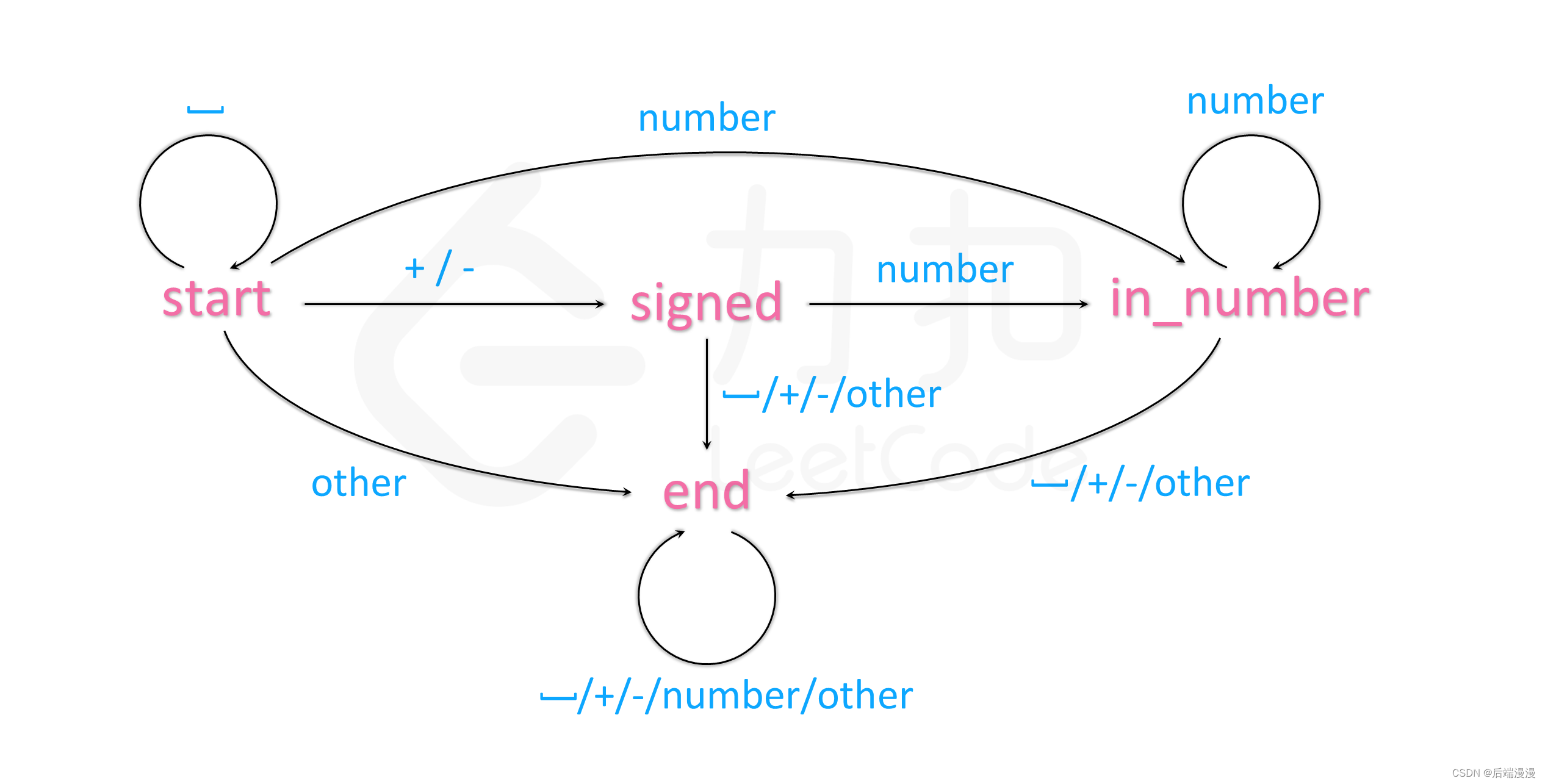
自动机,即有限状态机
文章目录一、问题来源二、题目描述三、题解中的自动机四、自动机学习五、有限状态机的使用场景一、问题来源 今天做力克题目的时候看到了字符串转换整数的一道算法题,其中又看到了题解中有自动机的概念,所以在这里对自动机做个笔记。题目链接 二、题目描…...
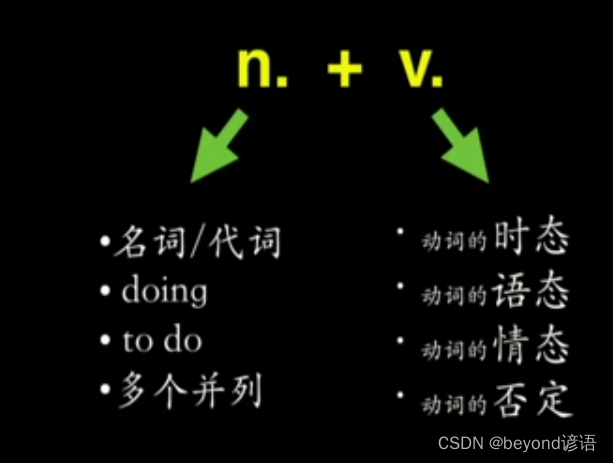
第一部分:简单句——第一章:简单句的核心——二、简单句的核心变化(主语/宾语/表语的变化)
二、简单句的核心变化 简单句的核心变化其实就是 一主一谓(n. v.) 表达一件事情,谓语动词是其中最重要的部分,谓语动词的变化主要有四种:三态加一否(时态、语态、情态、否定),其中…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
