用Vue3和Plotly.js绘制交互式3D烛形图

本文由ScriptEcho平台提供技术支持
项目地址:传送门
Plotly.js实现交互式K线图
应用场景
K线图广泛应用于金融领域,用于展示股票、外汇等金融产品的价格走势。它直观地呈现了开盘价、收盘价、最高价和最低价等信息,帮助投资者分析市场趋势和做出交易决策。
基本功能
本代码使用Plotly.js库创建了一张交互式的K线图,具有以下基本功能:
- **数据可视化:**绘制K线,显示股票价格的开盘价、收盘价、最高价和最低价。
- **交互式缩放:**允许用户通过拖拽或使用滑块来放大或缩小图表。
- **时间范围选择:**用户可以通过滑块选择特定的时间范围来查看K线图。
- **无图例:**为了保持图表简洁,移除了图例。
功能实现步骤及关键代码分析
1. 数据准备
首先,定义了K线图的数据,包括日期、开盘价、收盘价、最高价和最低价。
var trace1 = {x: ['...'], // 日期open: ['...'], // 开盘价high: ['...'], // 最高价low: ['...'], // 最低价close: ['...'], // 收盘价type: 'candlestick', // K线类型xaxis: 'x', // x轴关联yaxis: 'y' // y轴关联
};
2. 图表布局
接下来,定义了图表布局,包括边距、拖拽模式、x轴和y轴属性。
var layout = {dragmode: 'zoom', // 拖拽模式margin: {r: 10, // 右边距t: 25, // 上边距b: 40, // 下边距l: 60 // 左边距},showlegend: false, // 隐藏图例xaxis: {autorange: true, // 自动调整x轴范围domain: [0, 1], // x轴占据整个图表宽度range: ['...', '...'], // x轴时间范围rangeslider: {range: ['...', '...']}, // x轴滑块时间范围title: 'Date', // x轴标题type: 'date' // x轴类型为日期},yaxis: {autorange: true, // 自动调整y轴范围domain: [0, 1], // y轴占据整个图表高度range: [114.609999778, 137.410004222], // y轴价格范围type: 'linear' // y轴类型为线性}
};
3. 渲染图表
最后,使用Plotly.js的newPlot方法将数据和布局渲染到指定DOM元素中。
Plotly.newPlot('myDiv', data, layout);
总结与展望
开发这段代码的过程让我对Plotly.js库有了更深入的理解。我学会了如何使用Plotly.js创建交互式K线图,并定制其外观和功能。
未来,该卡片功能可以拓展和优化:
-
**增加技术指标:**添加技术指标,如移动平均线、布林带等,帮助用户分析市场趋势。
-
**提供更多数据源:**允许用户选择不同的股票或外汇产品,以查看K线图。
-
**实现实时更新:**通过Websocket或其他技术,实现K线图的实时更新,让用户及时了解市场动态。
更多组件:

</a>
获取更多Echos
本文由ScriptEcho平台提供技术支持
项目地址:传送门
扫码加入AI生成前端微信讨论群:

相关文章:

用Vue3和Plotly.js绘制交互式3D烛形图
本文由ScriptEcho平台提供技术支持 项目地址:传送门 Plotly.js实现交互式K线图 应用场景 K线图广泛应用于金融领域,用于展示股票、外汇等金融产品的价格走势。它直观地呈现了开盘价、收盘价、最高价和最低价等信息,帮助投资者分析市场趋势…...
git上传文件
git init git add . git commit -m " " git remote add origin 仓库的地址 git push -u origin master 如果出现以下问题 可以用这一句强制上传 git push -f origin master...

Redis 7.x 系列【16】持久化机制之 AOF
有道无术,术尚可求,有术无道,止于术。 本系列Redis 版本 7.2.5 源码地址:https://gitee.com/pearl-organization/study-redis-demo 文章目录 1. 概述2. 执行原理2.1 Redis 6.x2.1.1 直接写2.1.2 重写 2.2 Redis 7.x2.2.1 直接写2…...

使用 PostGIS 生成矢量图块
您喜欢视听学习吗?观看视频指南! 或者直接跳到代码 Overture Maps Foundation是由亚马逊、Meta、微软和 tomtom 发起的联合开发基金会项目,旨在创建可靠、易于使用、可互操作的开放地图数据。 Overture Maps 允许我们以GeoJSON格式下载开放…...

WebSocket 心跳机制如何实现
是一种简单并且有效的策略,用于维持长链接的活跃状态,防止因为网络空闲或者不稳定因素,导致链接意外中断。通过周期性的心跳消息,确保了链接的持久性和周期性,是维持实时通信服务稳定运行的关键组件。 1. 定时发送心跳…...

Docker 容器连接
Docker 容器连接 引言 在当今的软件开发和运维领域,Docker 已经成为了一个不可或缺的工具。它通过容器化的方式,为开发者提供了一种轻量级、可移植的计算环境。然而,要充分发挥 Docker 的潜力,我们需要掌握如何连接这些容器。本文将深入探讨 Docker 容器连接的概念、方法…...

【C语言】continue 关键字
当在C语言中使用continue关键字时,它用于控制循环语句的执行流程。与break不同,continue不会终止整个循环,而是终止当前迭代,并立即开始下一次迭代。这种行为使得可以在循环内部根据特定条件跳过某些代码块,从而控制程…...
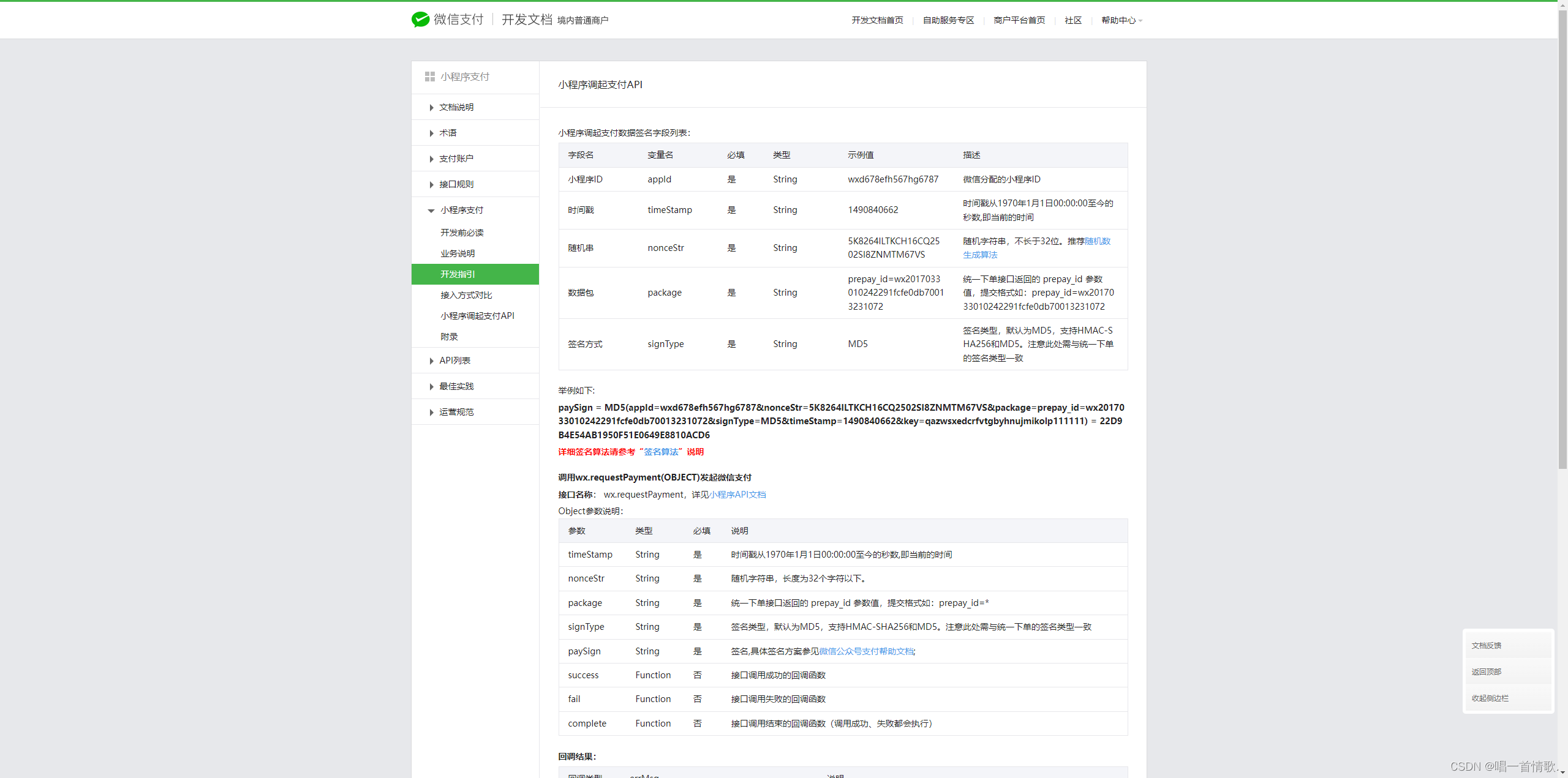
Taro + vue3 中微信小程序中实现拉起支付
在前端开发中 H5 的拉起支付和微信小程序的拉起支付 是不太一样的 现在分享一下微信小程序中的拉起支付 逻辑都在后端 我是用的Taro 框架 其实就是一个Api Taro 文档...

003-GeoGebra如何无缝嵌入到PPT里
GeoGebra无缝嵌入到PPT里真是一个头疼的问题,已成功解决,这里记录一下,希望可以帮助到更多人。 注意,后续所有的文章说的PPT都是Offce Power Point, 不要拿着WPS的bug来问我哦,我已经戒WPS了(此处表示无奈&…...

AI:开发者的朋友还是对手?
AI是在帮助开发者还是取代他们? 在软件开发领域,生成式人工智能(AIGC)正在改变开发者的工作方式。无论是代码生成、错误检测还是自动化测试,AI工具正在成为开发者的得力助手。然而,这也引发了对开发者职业…...

如何在Android Studio中查看APP客户端日志
测试Android应用时,日志查看是一个至关重要的调试工具,它帮助测试人员快速定位问题。幸运的是,Android Studio为我们提供了一个强大的工具——Logcat,使得查看运行时日志变得直接且简单。本文将引导你如何在Android Studio中使用L…...
2024微信小程序期末大作业-点奶茶微信小程序(后端nodejs-server)(附下载链接)_微信小程序期末大作业百度网盘下载
菜单展示 购物车展示: 提交订单: 支付详情页展示: 订单查看: 查看历史消费: 部分代码展示: <!--pages/home/home.wxml--> <block wx:for"{{listData}}" wx:key"itemlist&qu…...
Qt:4.信号和槽
目录 1.信号源、信号和槽: 2.Qt类的继承关系: 3.自定义槽函数: 4.第一种信号和槽的连接的方法: 5.第二种信号和槽的连接的方法: 6.自定义信号: 7.发射信号: 8.信号和槽的传参:…...

Ubuntu20.04更新GLIBC到2.35版本
目录 1 背景2 增加源2.1 标准源2.2 镜像源 3 更新 1 背景 Ubuntu20.04默认GLIBC库版本是2.31.今天碰到一个软件需要2.35版本的GLIBC。 升级GLIBC库有两种方式: 下载高版本库源码,编译后替换系统中低版本库。由于GLIBC库是Linux系统中最基础库ÿ…...
元对象系统 | 7.1、简介)
Qt 实战(7)元对象系统 | 7.1、简介
文章目录 一、简介1、元对象系统的基本条件2、元对象系统的核心功能3、元对象系统的核心类4、总结 Qt的元对象系统(Meta-Object System)是Qt框架中一个极其重要的组成部分,它为Qt提供了信号与槽机制、实时类型信息(RTTI࿰…...

iOS 真机打包,证书报错No signing certificate “iOS Distribution” found
之前将APP从旧账号转移到了新账号,在新账号打包的时候遇到的证书问题。 因为新账号还没有导出“本地签名证书”,也还没有创建新的“发布证书”。当我创建好这两者之后,在xcode打包的时候就报错了。 报错信息: No signing certifi…...

2024年7月3日 (周三) 叶子游戏新闻
老板键工具来唤去: 它可以为常用程序自定义快捷键,实现一键唤起、一键隐藏的 Windows 工具,并且支持窗口动态绑定快捷键(无需设置自动实现)。 卸载工具 HiBitUninstaller: Windows上的软件卸载工具 《魅魔》新DLC《Elysian Fields…...

linux守护进程生命周期管理-supervisord
简介 supervisor是一个client/server系统,允许用户控制多个类unix系统的进程,摆脱rc.d脚本的不方便性.supervisor具有简单,集中化管理,搞笑,可扩展性,高兼容. 整套软件包含:supervisord(守护进程),supervisorctl(命令行工具),web server(一个web交互界面),XML-RPC 交互 安装 …...

rtpengine_mr12.0 基础建设容器运行
目录 Dockerfile rtpengine.conf 容器内编译安装 RTPEngine 正常提供功能 1. 启动RTPEngine服务 2. 删除 RTPEngine服务 3. 加载内核模块 检查所有进程是否正在运行 上传到仓库 博主wx:yuanlai45_csdn 博主qq:2777137742 后期会创建粉丝群&…...

逐步深入:掌握sklearn中的增量学习
🚀 逐步深入:掌握sklearn中的增量学习 在机器学习领域,增量学习(也称为在线学习)是一种重要的学习方式,它允许模型在新数据到来时进行更新,而不需要重新训练整个数据集。这对于处理大量数据或实…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
