极紫外光源高次谐波发生腔不同区域真空度精密控制解决方案

摘要:在高次谐波发生器中一般包含两个不同真空区域,一个是1~100Torr绝压范围的气池内部的低真空区域,一个是高阶谐波光路上的绝压为0.001Pa量级的高真空区域。本文针对此两个区域的真空度控制提出了相应的解决方案,特别是详细介绍了气池内部的低真空度精密控制技术,控制精度可达到±1%以内,为各种高次谐波的产生提供了有效的技术保障。
原文阅读:(PDF格式)
1. 问题的提出
近年来,利用超短脉冲激光激发惰性气体产生高次谐波,为时间分辨及角分辨光电子能谱系统和极紫外光相干衍射成像提供了简单,成本可控的极紫外光源。高次谐波的产生是一个极端的非线性光学过程,其关键是要将强激光脉冲聚焦到可控浓度的惰性气体中。
如图1所示是一个高阶谐波在相干衍射成像中应用的典型结构示意图,其中超短脉冲激光被聚焦在充满惰性气体的气池内从而激发出高阶谐波。

在高次谐波生成过程中,要达到实际应用效果,相应的真空系统需要满足以下要求:
(1)在高次谐波产生过程中,宏观参数的变化会影响到原子密度和电离分数,并可实现相应的宏观相位匹配,因此可以使用对宏观参数例如有效相互作用长度、激光强度和气体压力的适当调整来改变高次谐波光谱。当改变这些参数时,不仅谐波阶数会改变,而且特定光谱范围内的光谱权重也会改变,这就意味着气池内部气体压力(真空度)需要具备可精密调节和稳定控制能力,以便实现所需高次谐波的产生。
(2)因高次谐波很容易被大气吸收,这就要求高次谐波的光路必须维持在高真空状态。
由此可见,在高次谐波发生器中需要包含两个不同真空度的区域,一个是1~100Torr绝对压力范围的气池内部低真空区域,另一个是高阶谐波光路上的绝对压力0.001Pa量级的高真空区域。本文将针对此两个不同区域的真空度控制提出相应的解决方案,特别是详细介绍了气池内部低真空区域内真空度的稳定精密控制。
2. 解决方案
为了解决高阶谐波发生器中双区域内的真空度控制问题,基于图1所示的用于相干衍射成像的高阶谐波发生器,本文提出的具体解决方案如图2所示。

在图2所示的真空控制系统中,根据真空度的不同将真空腔分为两个区域以分别用于气池和高阶谐波传输光路。针对这两个区域的真空度控制,采用了以下两个真空回路。
(1)光路的高真空控制回路
在真空腔的高真空回路中,排气管路直接与真空腔壁连接,通过分子泵来抽取真空腔内的气体使其达到绝压0.001Pa量级的高真空(图2中并未绘出相配套的低真空前级泵),同时用皮拉尼计来监控真空度的变化。为了在测试完成后取出样品,需要对真空腔进行充气以恢复到常压大气环境,在真空腔壁上布置了一个电动放气阀,可程序控制此放气阀的开启和关闭。
(2)气池的低真空控制回路
如图2所示,真空管路直接与气池连接,并与高压气瓶、调节进气流量的电动针阀、电容规、调节排气流量的电动针阀、干泵以及真空控制器组成低真空控制回路。对进气和排气流量进行调节以实现真空度控制是一种动态平衡控制方法,这种方法的特点是可实现1Pa~0.1MPa范围内真空度的精密控制,特别是结合24位AD和16位DA的双通道高精度真空度控制器,控制精度可达到±1%以内。
3. 总结
通过上述的两路独立真空控制回路构成的真空控制系统,可以很好的实现高次谐波发生器所需的真空度准确控制,而且气池内的真空度可以任意调节和恒定控制,为各种高次谐波的产生和优化提供了有效的技术保障。

相关文章:

极紫外光源高次谐波发生腔不同区域真空度精密控制解决方案
摘要:在高次谐波发生器中一般包含两个不同真空区域,一个是1~100Torr绝压范围的气池内部的低真空区域,一个是高阶谐波光路上的绝压为0.001Pa量级的高真空区域。本文针对此两个区域的真空度控制提出了相应的解决方案,特别是详细介绍…...

「Vue面试题」在vue中为什么data属性是一个函数而不是一个对象
文章目录一、实例和组件定义data的区别二、组件data定义函数与对象的区别三、原理分析四、结论一、实例和组件定义data的区别 vue实例的时候定义data属性既可以是一个对象,也可以是一个函数 const app new Vue({el:"#app",// 对象格式data:{foo:"…...
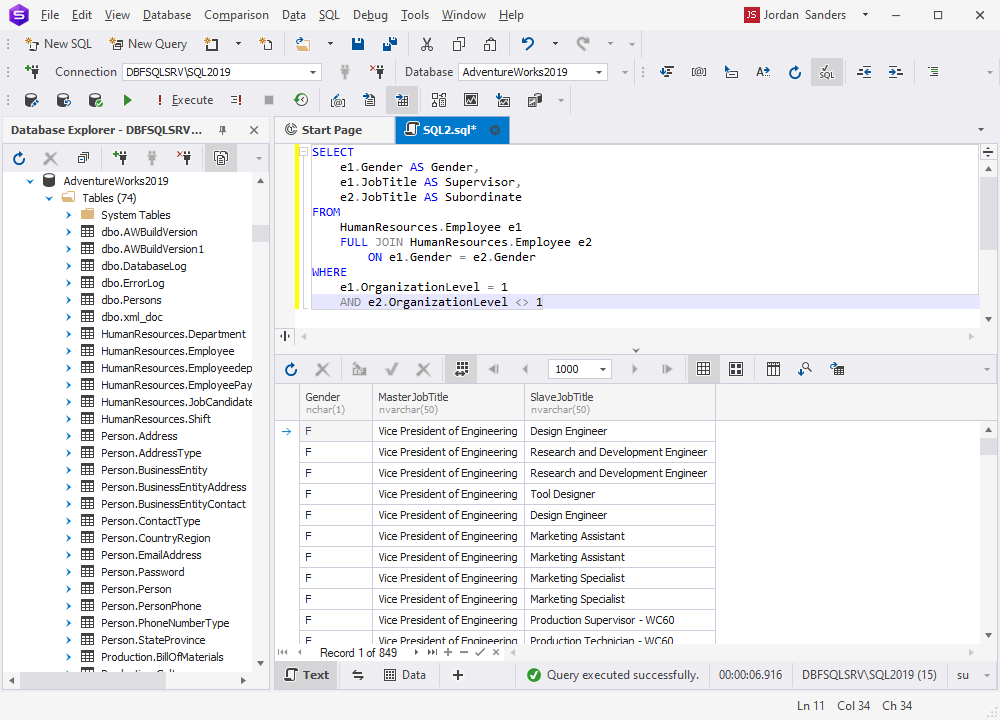
如何使用 ChatGPT 编写 SQL JOIN 查询
通过清晰的示例和解释,本文展示了 ChatGPT 如何简化和简化创建复杂 MySQL 查询的过程,使用户更容易与数据库交互并检索他们需要的数据。无论您是初学者还是经验丰富的开发人员,本文都提供了有关如何利用 ChatGPT 来增强您的 MySQL 查询编写技…...
vue2+elementUI完成添加学生删除学生案列
效果图: 点击添加学生按钮,弹出Dialog,收集用户信息: el-table中自定义复选框,选中一行,可以点击删除 代码区域:就一个HTML文件 <!DOCTYPE html> <html lang"en"> <head>&…...

对void的深度理解
作者:小树苗渴望变成参天大树 作者宣言:认真写好每一篇博客 作者gitee:gitee 如 果 你 喜 欢 作 者 的 文 章 ,就 给 作 者 点 点 关 注 吧! void前言一、 void 关键字二、 void修饰函数返回值和参数三、void指针3.1void * 定义的…...

哪款游戏蓝牙耳机好用?好用的游戏蓝牙耳机推荐
现在,不少人喜欢戴蓝牙耳机玩游戏,而在戴蓝牙耳机玩游戏时难免会产生音画不同步的问题。现在越来越多的蓝牙耳机支持游戏模式,那么,哪款游戏蓝牙耳机好用?接下来,我来给大家推荐几款好用的游戏蓝牙耳机&…...

求职(怎么才算精通JAVA开发)
在找工作的的时候,有时候我们需要对自己的技术水平做一个评估。特别是Java工程师,我们该怎么去表达自己的能力和正确认识自己所处的技术水平呢。技术一般的人,一般都不敢说自己精通JAVA,因为你说了精通JAVA几乎就给了面试官一个可以随便往死里问的理由了。很多不自信的一般…...
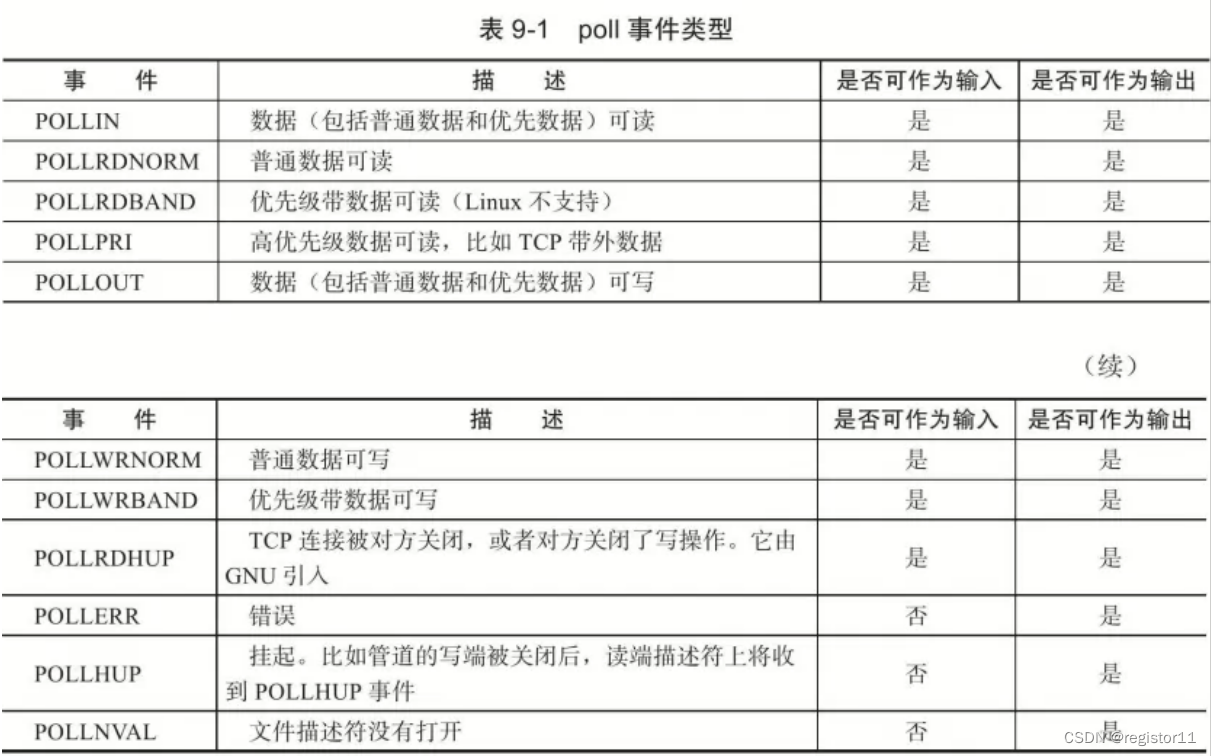
C++网络编程(三)IO复用
C网络编程(三)IO复用 前言 多进程/多线程网络服务端在创建进程/线程时,CPU和内存开销很大。因为多线程/进程并发模型,为每个socket分配一个线程/进程。而IO复用采用单个的进程/线程就可以管理多个socket。 select 系统调用原型: #includ…...
模拟赛试题与题解 C++)
第十四届蓝桥杯(第三期)模拟赛试题与题解 C++
第十四届蓝桥杯(第三期)模拟赛试题与题解 C 试题 A 【问题描述】 请找到一个大于 2022 的最小数,这个数转换成十六进制之后,所有的数位(不含前导 0)都为字母(A 到 F)。 请将这个…...

【Hive 基础】-- 数据倾斜
1.什么是数据倾斜?由于数据分布不均匀,导致大量数据集中到一点,造成数据热点。常见现象:一个 hive sql 有100个 map/reducer task, 有一个运行了 20分钟,其他99个 task 只运行了 1分钟。2.产生数据倾斜的原…...
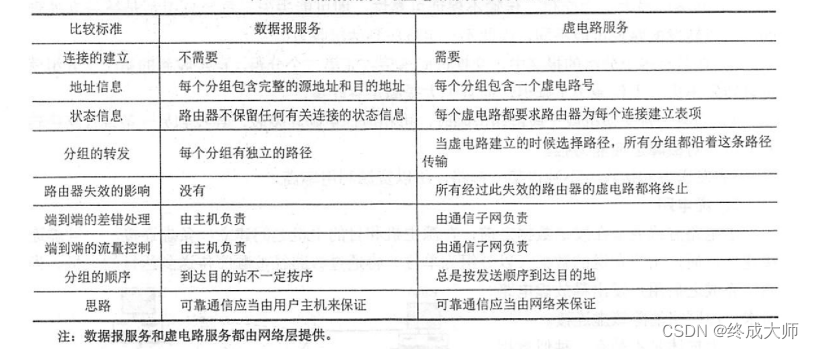
计算机网络笔记——物理层
计算机网络笔记——物理层2. 物理层2.1 通信基础2.1.1 信号2.1.2 信源、信道及信宿2.1.3 速率、波特及码元2.1.4 带宽2.1.5 奈奎斯特定理采样定理奈奎斯特定理2.1.6 香农定理2.1.7 编码与调制调制数字信号调制为模拟信号模拟数据调制为模拟信号编码数字数据编码为数字信号模拟数…...
算法第十七期——状态规划(DP)之动态压缩
一、总述 状态压缩动态规划,就是我们俗称的状压DP,是利用计算机二进制的性质来描述状态的一种DP方式。 应用背景:以集合为状态,且集合可以用二进制来表示,用二进制的位运算来处理。集合问题一般是指数复杂度的&#x…...
网络安全竞赛试题A模块第八套解析(详细))
2022年全国职业院校技能大赛(中职组)网络安全竞赛试题A模块第八套解析(详细)
2022年全国职业院校技能大赛(中职组) 网络安全竞赛试题 (8) (总分100分) 赛题说明 一、竞赛项目简介 “网络安全”竞赛共分A.基础设施设置与安全加固;B.网络安全事件响应、数字取证调查和应用安全;C.CTF夺旗-攻击;D.CTF夺旗-防御等四个模块。根据比赛实际情况,竞…...

【华为OD机试真题 JAVA】数组中是否存在满足规则的数字组合
标题:数组中是否存在满足规则的数字组合 | 时间限制:1秒 | 内存限制:262144K | 语言限制:不限 给定一个正整数数组,检查数组中是否存在满足规则的数字组合 * 规则: * A = B + 2C 输入描述: * 第一行输出数组的元素个数。 * 接下来一行输出所有数组元素,用空格…...

【OpenCV技能树】——OpenCV基础
前言: 😊😊😊欢迎来到本博客😊😊😊 目前正在进行 OpenCV技能树的学习,OpenCV是学习图像处理理论知识比较好的一个途径,至少比看书本来得实在。本专栏文章主要记录学习Op…...

人体姿态识别
自留记录论文阅读,希望能了解我方向的邻域前沿吧 粗读,持续更新 第一篇 ATTEND TO WHO YOU ARE: SUPERVISING SELF-ATTENTION FOR KEYPOINT DETECTION AND INSTANCE-AWARE ASSOCIATION 翻译:https://editor.csdn.net/md?not_checkout=1&spm=1001.2014.3001.5352&…...

ubuntu下调试驱动
使用 Ubuntu Linux 测试 Linux 驱动 1. 测试 Linux 驱动准备工作 对于一个 Linux 驱动程序,一开始可以在 Ubuntu Linux 上做前期开发和测试。对于访问硬件部分也可以在 Ubuntu Linux 用软件进行模拟,切记不能代替真实的环境!当基本开发完成后&#…...
第十四届蓝桥杯三月真题刷题训练——第 9 天
第 1 题:找素数 题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 素数就是不能再进行等分的整数。比如:7,11。而 9 不是素数,因为它可以平分为 3 等份。一般认为最小的…...

操作系统复习
熟练掌握操作系统的定义,操作系统的特征,操作系统的功能熟练掌握多道程序设计的概念,单道程序设计和多道程序设计的区别,多道程序设计的优点熟悉操作系统接口的主要功能,系统调用的基本概念、类型、实现。操作系统接口…...
springboot健身房管理系统
springboot健身房管理系统 ✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
