C++(Python)肥皂泡沫普拉托边界膜曲面模型算法
🎯要点
🎯肥皂泡二维流体模拟 | 🎯泡沫普拉托边界膜曲面模型算法演化厚度变化 | 🎯螺旋曲面三周期最小结构生成
📜皂膜用例:Python计算物理粒子及拉格朗日和哈密顿动力学 | Python和MATLAB粘性力接触力动态模型半隐式欧拉算法


🍇Python(MATLAB)三维曲面图
普拉托定律描述了肥皂膜的结构。这些定律是由比利时物理学家普拉托在 19 世纪根据他的实验观察制定的。自然界中的许多图案都是基于遵守这些定律的泡沫。此定律描述了皂膜的形状和构造如下:
- 肥皂膜由整个(完整的)光滑表面制成
- 肥皂膜的一部分的平均曲率在同一块肥皂膜上的任何点处处处恒定
- 肥皂膜总是沿着称为普拉托边界的边缘成三块相交,并且它们以 arccos(− 1 / 2 ) = 120°‘
- 这些普拉托边界在一个顶点处以四面体角 arccos(− 1 / 3 ) ≈ 109.47°。
除普拉托定律之外的结构是不稳定的,并且薄膜将很快倾向于重新排列自身以符合这些定律。美国数学家吉恩·艾伦·泰勒使用几何测量理论在数学上证明了这些定律适用于最小曲面。
肥皂膜是被空气包围的薄层液体(通常为水基)。例如,如果两个肥皂泡接触,它们会合并并在其间形成一层薄膜。因此,泡沫由通过普拉托边界连接的薄膜网络组成。肥皂膜可用作极小曲面的模型系统,极小曲面在数学中被广泛使用。
从数学角度来看,肥皂膜是最小表面。表面张力是单位面积产生表面所需的能量。薄膜——与任何物体或结构一样——倾向于以最小势能状态存在。为了最小化其能量,自由空间中的液滴自然呈现球形,对于给定的体积,其表面积最小。水坑和薄膜可以在其他力的存在下存在,例如重力和对基质原子的分子间吸引力。后一种现象称为润湿:基质原子和薄膜原子之间的结合力会导致总能量降低。在这种情况下,物体的最低能量配置是尽可能多的薄膜原子尽可能靠近基质。这将导致无限薄的薄膜,无限广泛地分布在基质上。实际上,粘附润湿效应(导致表面最大化)和表面张力效应(导致表面最小化)会相互平衡:稳定的结构可以是液滴、水坑或薄膜,具体取决于作用于身体的力。
💦Python绘制三维曲面:
Matplotlib 的 mpl_toolkits.mplot3d 工具包中的 axis3d 提供了用于创建三维曲面图的必要函数。曲面图是通过使用 ax.plot_surface() 函数创建的。
语法:
ax.plot_surface(X, Y, Z)
其中 X 和 Y 是 x 和 y 点的二维数组,而 Z 是高度的二维数组。
示例:
# Import libraries
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as pltx = np.outer(np.linspace(-3, 3, 32), np.ones(32))
y = x.copy().T # transpose
z = (np.sin(x **2) + np.cos(y **2) )fig = plt.figure(figsize =(14, 9))
ax = plt.axes(projection ='3d')ax.plot_surface(x, y, z)
plt.show()
梯度曲面图是三维曲面图与二维轮廓图的组合。在此图中,三维曲面的颜色与二维轮廓图相同。曲面较高的部分与曲面较低的部分颜色不同。
语法:
surf = ax.plot_surface(X, Y, Z, cmap=, linewidth=0, antialiased=False)
属性 cmap= 设置表面的颜色。还可以通过调用Fig.colorbar来添加颜色条。下面的代码创建一个梯度曲面图:
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as pltx = np.outer(np.linspace(-3, 3, 32), np.ones(32))
y = x.copy().T # transpose
z = (np.sin(x **2) + np.cos(y **2) )fig = plt.figure(figsize =(14, 9))
ax = plt.axes(projection ='3d')
my_cmap = plt.get_cmap('hot')surf = ax.plot_surface(x, y, z,cmap = my_cmap,edgecolor ='none')fig.colorbar(surf, ax = ax,shrink = 0.5, aspect = 5)ax.set_title('Surface plot')
plt.show()使用 Matplotlib 绘制的三维曲面图可以投影到二维曲面上。下面的代码创建三维图并可视化其在二维等高线图上的投影:
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as pltx = np.outer(np.linspace(-3, 3, 32), np.ones(32))
y = x.copy().T # transpose
z = (np.sin(x **2) + np.cos(y **2) )fig = plt.figure(figsize =(14, 9))
ax = plt.axes(projection ='3d')my_cmap = plt.get_cmap('hot')surf = ax.plot_surface(x, y, z, rstride = 8,cstride = 8,alpha = 0.8,cmap = my_cmap)
cset = ax.contourf(x, y, z,zdir ='z',offset = np.min(z),cmap = my_cmap)
cset = ax.contourf(x, y, z,zdir ='x',offset =-5,cmap = my_cmap)
cset = ax.contourf(x, y, z, zdir ='y',offset = 5,cmap = my_cmap)
fig.colorbar(surf, ax = ax, shrink = 0.5,aspect = 5)ax.set_xlabel('X-axis')
ax.set_xlim(-5, 5)
ax.set_ylabel('Y-axis')
ax.set_ylim(-5, 5)
ax.set_zlabel('Z-axis')
ax.set_zlim(np.min(z), np.max(z))
ax.set_title('3D surface having 2D contour plot projections')plt.show()
💦MATLAB最小曲面
构造最小曲面
n=35;
[X,Y,Z]=meshgrid(linspace(-pi,pi,n));
[F,V] = isosurface(X,Y,Z,S,0);
曲面可视化
cFigure;
hold on;
title('Schwarz P-surface','FontSize',fontSize);
gpatch(F,V,'kw','k',1);
axisGeom;
camlight headlight;
drawnow;
可视化曲面所有变体:
cFigure;subplot(2,3,1);
title('Schwarz P-surface','FontSize',fontSize);
hold on;
gpatch(F,V,pColors(1,:),'none',1);
axisGeom;
camlight headlight; lighting gouraud;
view(-50,30);[X,Y,Z]=meshgrid(linspace(-pi,pi,n));
[F,V] = isosurface(X,Y,Z,S,0.1);subplot(2,3,2);
title('d','FontSize',fontSize);
hold on;
gpatch(F,V,pColors(2,:),'none',1);
axisGeom;
camlight headlight; lighting gouraud;
view(-50,30);[X,Y,Z]=meshgrid(linspace(-2*pi,2*pi,n));
[F,V] = isosurface(X,Y,Z,S,0.6);subplot(2,3,3);
title('Gyroid','FontSize',fontSize);
hold on;
gpatch(F,V,pColors(3,:),'none',1);
axisGeom;
camlight headlight; lighting gouraud;
view(-50,30);[X,Y,Z]=meshgrid(linspace(-pi,pi,n));
[F,V] = isosurface(X,Y,Z,S,0);subplot(2,3,4);
title('Neovius','FontSize',fontSize);
hold on;
gpatch(F,V,pColors(4,:),'none',1);
axisGeom;
camlight headlight; lighting gouraud;
view(-50,30);[X,Y,Z]=meshgrid(linspace(-pi,pi,n));
[F,V] = isosurface(X,Y,Z,S,0);subplot(2,3,5);
title('w','FontSize',fontSize);
hold on;
gpatch(F,V,pColors(5,:),'none',1);
axisGeom;
camlight headlight; lighting gouraud;
view(-50,30);[X,Y,Z]=meshgrid(linspace(-pi,pi,n));
[F,V] = isosurface(X,Y,Z,S,0.5);subplot(2,3,6);
title('pw','FontSize',fontSize);
hold on;
gpatch(F,V,pColors(6,:),'none',1);
axisGeom;
camlight headlight; lighting gouraud;
view(-50,30);
drawnow;
👉参阅:计算思维 | 亚图跨际
相关文章:

C++(Python)肥皂泡沫普拉托边界膜曲面模型算法
🎯要点 🎯肥皂泡二维流体模拟 | 🎯泡沫普拉托边界膜曲面模型算法演化厚度变化 | 🎯螺旋曲面三周期最小结构生成 📜皂膜用例:Python计算物理粒子及拉格朗日和哈密顿动力学 | Python和MATLAB粘性力接触力动…...

VBA打开其他Excel文件
前言 本节会介绍通过VBA实现打开其他excel文件,包括模糊匹配文件名称、循环同时打开多个文件,并获取工作表及工作簿进行数据操作后,对打开的文件进行保存并关闭操作。 一、打开固定文件名称的文件 场景说明: 1.新建一个宏文件VBA…...
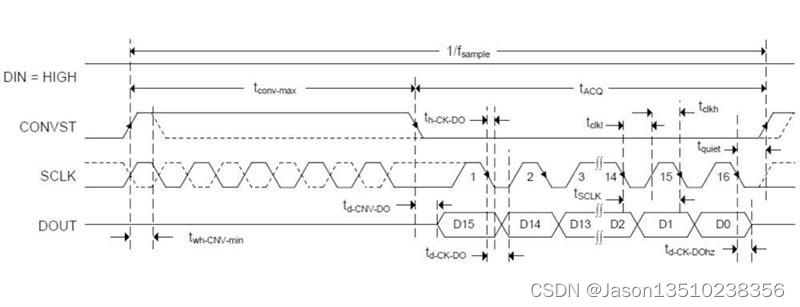
模拟 ADC 的前端
ADC 的 SPICE 模拟 反复试验的方法将信号发送到 ADC 非常耗时,而且可能有效也可能无效。如果转换器捕获电压信息的关键时刻模拟输入引脚不稳定,则无法获得正确的输出数据。SPICE 模型允许您执行的步是验证所有模拟输入是否稳定,以便没有错误…...

tls各个版本的安全性介绍
TLS(Transport Layer Security)协议的各个版本在安全性方面经历了逐步的演进和改进,以应对不断变化的网络安全威胁。以下是各主要版本的安全性概览: TLS 1.0: 发布于1999年,是SSL 3.0的后续版本。在其发布时…...
PHP家政服务预约单开版微信小程序系统源码
🏠 —— 便捷生活,从指尖开始💪 🌈【开篇:家政新风尚,一键触达】 在忙碌的生活节奏中,你是否渴望拥有一个温馨、整洁的家,却又苦于找不到合适的家政服务?现在ÿ…...

数据增强:目标检测算法中的性能提升利器
引言 目标检测是计算机视觉领域的核心任务之一,旨在从图像或视频中识别和定位感兴趣的对象。然而,由于训练数据的局限性,目标检测模型往往面临过拟合和泛化能力不足的问题。数据增强作为一种有效的解决方案,通过增加数据多样性来…...

KVB交易平台 :市场迎来新热潮!铜价会持续上涨吗?
近期,全球铜价出现明显上涨趋势。韩国光阳LME仓库的铜库存显著下降,市场对即时需求的增加作出了积极反应。供应端的紧张和需求端的复苏共同推动了铜价的上涨。 KVB外汇 分析师们对未来铜价保持谨慎乐观态度,认为长期内铜价有望保持稳定甚至进…...

React@16.x(44)路由v5.x(9)源码(1)- path-to-regexp
目录 1,作用2,实现获取 match 对象2.1,match 对象的内容2.2,注意点2.3,实现 1,作用 之前在介绍 2.3 match 对象 时,提到了 react-router 使用第3方库 path-to-regexp 来匹配路径正则。 我们也…...
和String str = “a“有什么区别)
C#面:String str=new String(“a“)和String str = “a“有什么区别
String str new String(“a”)和String str “a”的区别在于对象的创建方式和内存分配方式。 字符串 str new String(“a”): 使用new关键字显式地创建了一个新的String对象。 每次执行这行代码时,都会…...

CS算法(二)—— 斜视SAR点目标仿真
SAR成像专栏目录 我们按照Cumming教授所著的《合成孔径雷达成像——算法与实现》7.6节的点目标参数进行仿真,斜视角设置为8,中心斜距改为1000km。先放最终的仿真结果: 1. 参数配置 在中心点和中心的的上下左右方向设置5个点目标 : function para=config_sar_para_cumming(…...

2024亚洲国际餐饮展览会(北京餐饮展|火锅展|预制菜展会)
2024北京餐饮展会,2024北京食材展会,2024北京火锅展会,2024北京火锅食材展会,2024北京预制菜展会,2024北京预制食材展会, 2024亚洲国际餐饮展览会(北京餐饮展|火锅展|预制菜展会) …...
【RabbitMQ问题踩坑】RabbitMQ设置手动ack后,消息队列有多条消息,只能消费一条,就不继续消费了,这是为什么 ?
现象:我发送5条消息到MQ队列中,同时,我在yml中设置的是需要在代码中手动确认,但是我把代码中的手动ack给关闭了,会出现什么情况? yml中配置,配置需要在代码中手动去确认消费者消费消息成功&…...

深度解码:需求跟踪的艺术与实战应用
文章目录 引言一、需求跟踪的定义二、需求跟踪矩阵2.1 需求跟踪矩阵包含的内容2.2 跟踪矩阵层级2.3 需求属性2.4 参考表格 三、需求跟踪的收益3.1 确保商业价值最大化3.2 满足客户期望3.3 范围管理3.4 决策支持3.5 提高效率和效果3.6 文档化和沟通3.7 变更管理3.8 测量和改进 四…...

数据结构——树的基础概念
目录 1.树的概念 2.树的相关概念 3.树的表示 (1)直接表示法 (2)双亲表示法 (3)左孩子右兄弟表示法 4.树在实际中的运用(表示文件系统的目录树结构) 1.树的概念 树是一种非线性的数据结构࿰…...

TimerManager和Timer
在RTSP服务器中需要一个定时器来定时发送音频帧和视频帧。音频帧每隔23ms发送一帧,视频帧每隔40ms发一帧。 因此需要两个定时器来定时发送,此时我们就需要用到一个TimerManager来管理Timer。 在TimerManager类中我们需要创建定时器文件描述符ÿ…...

手写Spring-MVC之前后置处理器与异常处理、数据库框架
Day48 手写Spring-MVC之前后置处理器与异常处理 前后置处理器 概念:从服务器获取的JSON数据可能是加密后的,因此服务端获取的时候需要进行解密(前置处理器)。 而从服务器传出的JSON数据可能需要加密,因此需要在处理返…...

学习笔记(linux高级编程)11
进程间通信 》信号通信 应用:异步通信。 中断,, 1~64;32应用编程。 如何响应: Term Default action is to terminate the process. Ign Default action is to ignore the signal. wait Core Default action is …...

vite+vue3+nginx配置统一公共前缀
方案1:重定向 server {listen 80;server_name localhost;location / {root /usr/share/nginx/html;index index.html;}location /music/ {proxy_pass http://127.0.0.1:80/;} }方案2:vitenginx双重配置 在方案1中,我们虽然能够实现 通过 …...

android 国内下载Gradle源
在中国使用 Gradle 时,可以配置使用一些国内的镜像源,以提高下载速度和稳定性。以下是几个常用的 Gradle 镜像源地址: 配置 gradle-wrapper.properties 文件: 阿里云: distributionUrlhttps\://services.gradle.org/distributions/gradle-7.…...
 拿走即用)
mysql8一键安装脚本(linux) 拿走即用
创建一个shell文件,将下面的代码放里面去,然后放到linux服务器上运行就可以了 #!/bin/bash#---------------------* # * # 2021-10-08 * # install mysql-8 * # * #---------------------*route=/usr #包存放路径 mys…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
