[数据结构】——七种常见排序
文章目录
- 前言
- 一.冒泡排序
- 二.选择排序
- 三.插入排序
- 四.希尔排序
- 五.堆排序
- 六.快速排序
- hoare
- 挖坑法
- 前后指针
- 快排递归实现:
- 快排非递归实现:
- 七、归并排序
- 归并递归实现:
- 归并非递归实现:
- 八、各个排序的对比图
前言
- 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小, 递增或递减的排列起来的操作。
- 稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
- 内部排序:数据元素全部放在内存中的排序。
- 外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序
接下来会涉及到的排序

这里写了一个测试排序性能的代码,方便我们观察各个排序的好坏
//测试排序的性能
void TestOP()
{srand((unsigned)time(NULL));//N的数值手动改变,以判断性能的好坏const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand() + i;a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();int begin7 = clock();BubbleSort(a7, N);int end7 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);printf("BubbleSort:%d\n", end7 - begin7);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);
}
还有交换函数
//交换函数
void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}
以下排序默认是升序,即从小到大的顺序
一.冒泡排序
冒泡的时间复杂度是O(N^2),空间复杂度是O(1),具有稳定性

从图中我们可以看出,冒泡排序其实就是一种选择排序,即走一次,找到最大的数放在最右边,接下来要排序的数据就少了一个,再走一次,找到此时最大的数放在此时的最右边,接下来不断重复此步骤,数据就有序了
//冒泡排序
void BubbleSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int flag = 0;for (int j = 0; j < n - 1 - i; j++){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);flag = 1;}}if (flag == 0){return;}}
}
虽然我们使用了flag进行了优化,使冒泡排序在最好的情况下的时间复杂度位O(N),但是实际上冒泡排序只有教学意义,没有实践意义,效率非常低
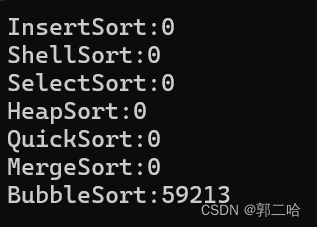
在十万个数据下面,冒泡走了5s,而在一百万数据下面,走了接近1min了,可见效率是如此的低下

二.选择排序
选择排序的时间复杂度是O(N^2),空间复杂度是O(1),具有不稳定性

从图中我们可以清楚的看到,选择排序每走一次,找到最大或者最小的数据放在最右边或者最左边,然后减少排序的个数,以此类推完成排序
这个排序方法可以优化一下,即走一次找到最小的同时找到最大的
//选择排序
void SelectSort(int* a, int n)
{int begin = 0;int end = n - 1;while (begin < end){int mini = begin;int maxi = begin;for (int i = begin + 1; i <= end; i++){if (a[i] < a[mini]){mini = i;}if (a[i] > a[maxi]){maxi = i;}}Swap(&a[begin], &a[mini]);if (maxi == begin){maxi = mini;}Swap(&a[end], &a[maxi]);begin++;end--;}
} 选择排序即没有实际意义,也没有教学意义,效率低下
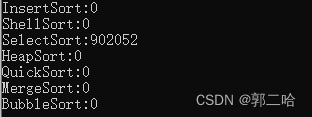
在十万个数据下面,选择走了8s,而在一百万数据下面,走了接近15min了,效率不行

三.插入排序
插入排序的时间复杂度是O(N^2),空间复杂度是O(1),具有稳定性

插入排序的思路就是假设在[0,end]是有序的数据,在end+1的位置上插入一个新的数据,用tmp保存插入的数据。
如果end位置上的值大于tmp,end就减1,比较此时end位置上的值与tmp的大小
如果end位置上的值小于tmp,退出循环,将tmp赋给end + 1 位置上的值
//插入排序
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;//[0,end]是有序的,插入[end+1]数据int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}
虽然插入排序的时间复杂度是O(N^2),但是它具有实践意义
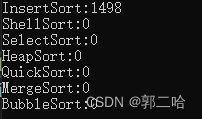
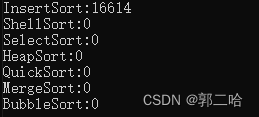
在十万个数据下面,走了1s,在一百万数据下面,走了16s了,可见效率是还可以
四.希尔排序
希尔排序的时间复杂度是O(N^1.3),空间复杂度是O(1),不具有稳定性

希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序,是直接插入排序算法的一种更高效的改进版本。
希尔排序的思想:
- 预排序:先分gap,在各自的组内进行插入排序
- 插入排序:排好序后,减小gap的值,再次进行预排序,直到gap = 1,进行插入排序,这样数据就有序了
假设gap = 3,将原数据分成3组,那么第一趟预排序的结果为下图
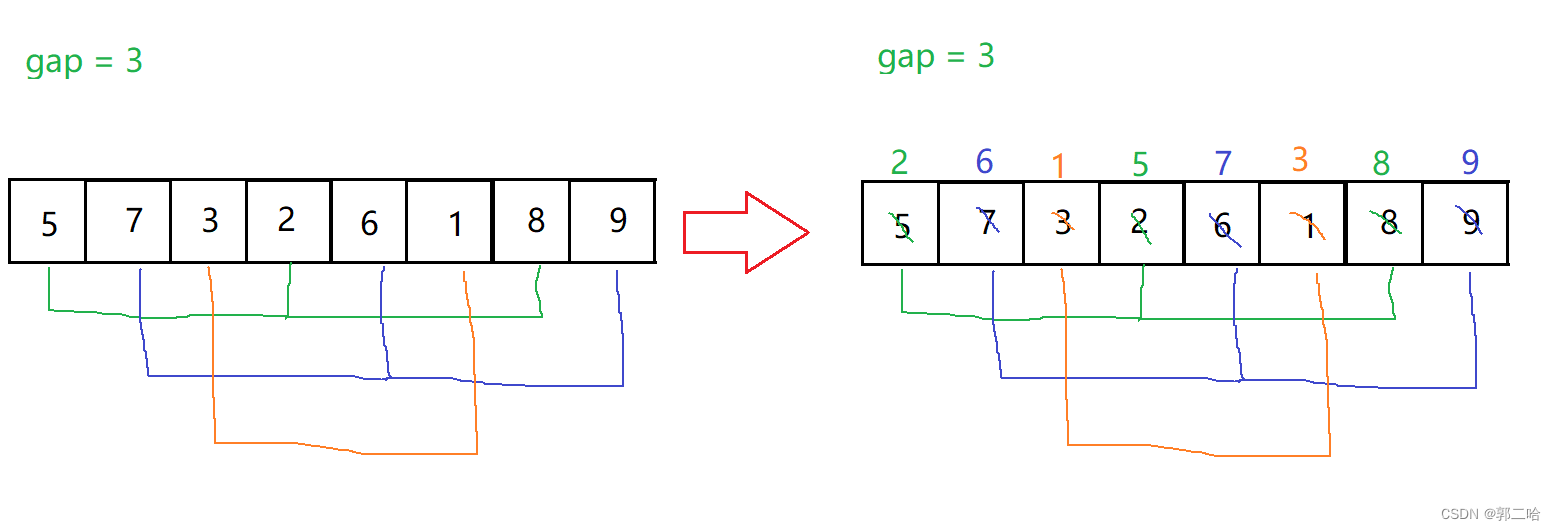
可以看到在走了一趟后的数据,比原始数据接近有序,这就是希尔排序的优点
//希尔排序
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;//多组一起走for (int i = 0; i < n-gap; i++){int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}
在十万个数据下面,希尔走了31ms,在一百万数据下面,走了264ms,可见效率还是很快的


五.堆排序
堆排序的时间复杂度是O(NlogN),空间复杂度是O(1),不具有稳定性

堆排序(Heap Sort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
堆排序的基本思想是:
- 将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。
- 将其与末尾元素进行交换,此时末尾就为最大值。
- 然后将剩余n-1 个元素重新构造成一个堆,这样会得到 n 个元素的次小值。 如此反复执行,便能得到一个有序序列了。
//向下调整法
void AdjustDown(int* a, int n, int parent)
{int child = 2 * parent + 1;while (child < n){if (child + 1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = 2 * parent + 1;}else{break;}}
}//堆排序
void HeapSort(int* a, int n)
{//创建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, n, i);}//排序int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);end--;}
}
在十万个数据下面,堆排走了45ms,在一百万数据下面,走了473ms,效率还可以


六.快速排序
快速排序的平均时间复杂度是O(NlogN),但是在最坏情况下有可能是O(N^2),空间复杂度是O(logN)~O(N),不具有稳定性

快速排序(Quick Sort)是一种常用的排序算法。快速排序的基本思想是通过选择一个基准元素,将数组分为两部分,使得左边的元素都小于等于基准元素,右边的元素都大于等于基准元素。然后,对左右两部分分别进行快速排序,直到整个数组有序。
但是当数组已经有序时是最坏情况,快速排序的时间复杂度可能会达到O(N^2)。但是,在大多数情况下,快速排序的时间复杂度都非常接近O (NlogN)
快速排序优化的方法:
1.三数取中
可以看到假定最左边的数作为基准元素,会不准确,因为有可能是最大的数也有可能是最小的数,影响效率,我们可以选择三个数中间的数来作为基准元素
//三数取中法 left midi right
int GetMidi(int* a,int left,int right)
{int midi = (left + right) / 2;if (a[left] > a[midi]){if (a[midi] >= a[right]){return midi;}else if (a[left] < a[right]){return left;}else{return right;}}else{if (a[midi] <= a[right]){return midi;}else if (a[left] > a[right]){return left;}else{return right;}}
}
2.小区间优化
由于快速排序要递归数据区间,只要递归就要消耗空间,那么当数据区间比较小时,可以用插入排序,不用在递归了
//小区间排序 -> 插入排序
if ((right - left + 1) < 10)
{//注意数组取的位置和数组的长度InsertSort(a+left, right - left + 1);
}
快速排序有三种排序方法:
hoare

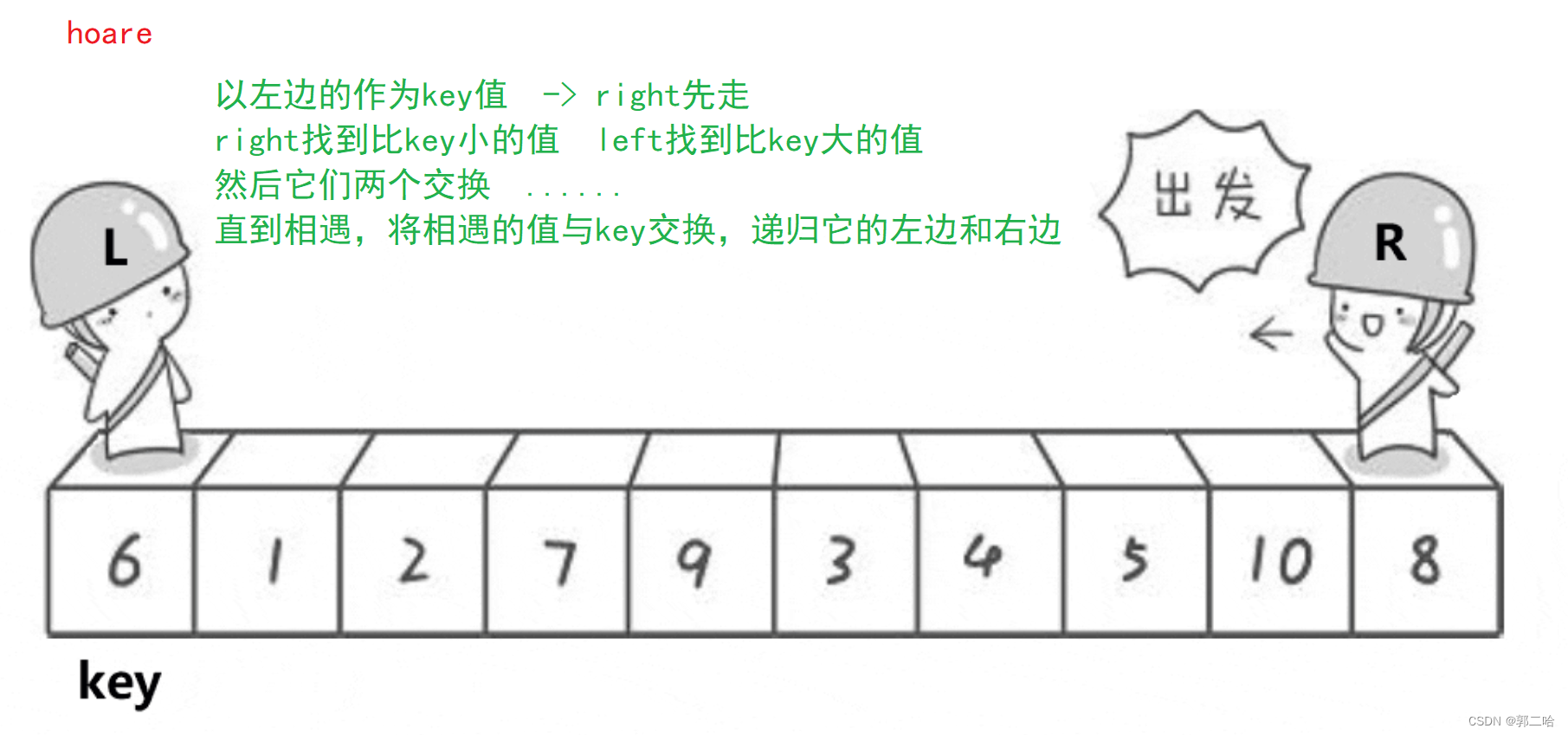
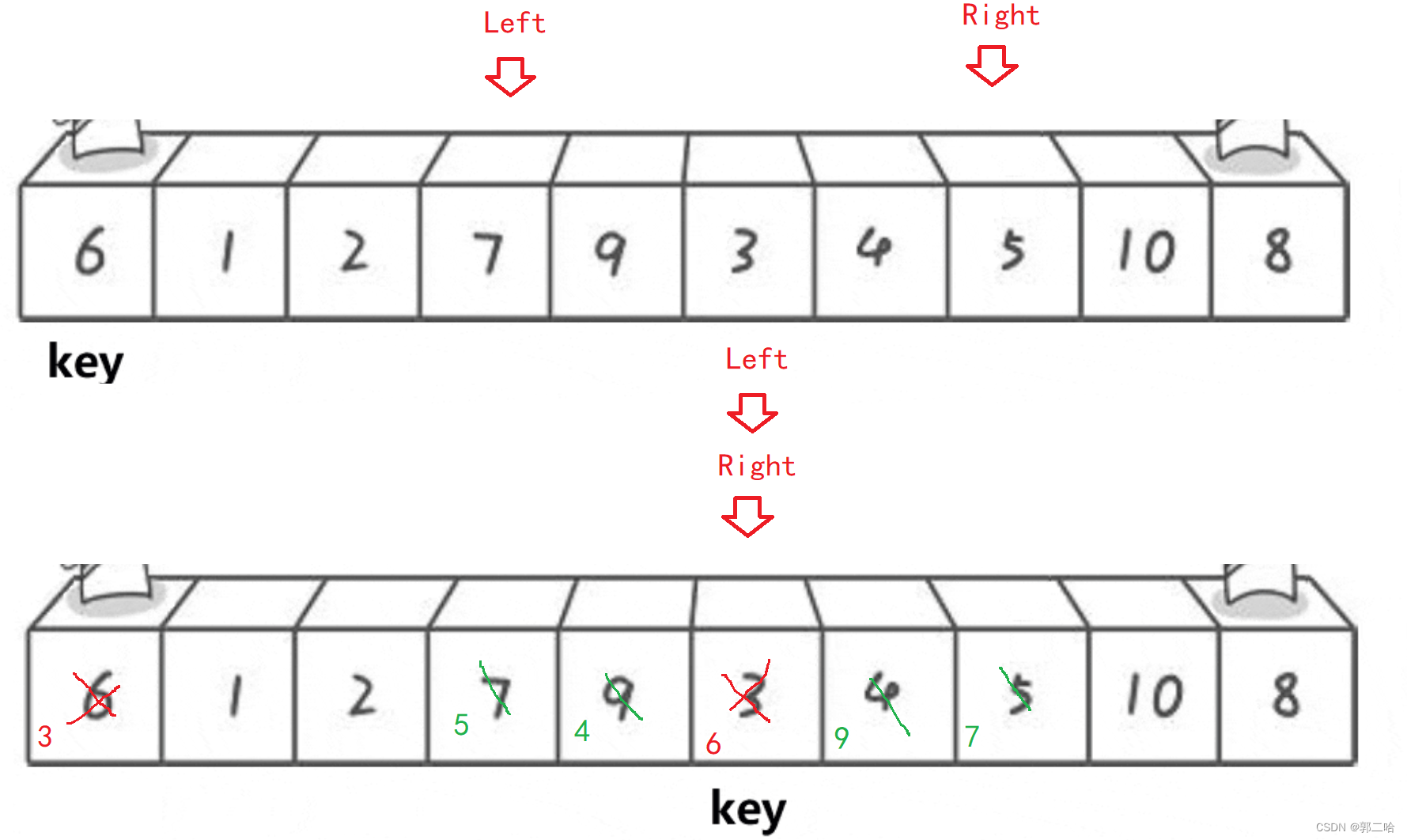
此时,数据6已经排好了,只需要递归它的左边与右边进行排序即可
// 快速排序hoare版本
int PartSort1(int* a, int left, int right)
{//三数取中int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;int begin = left;int end = right;while (begin < end){while (begin < end && a[end] >= a[keyi]){end--;}while (begin < end && a[begin] <= a[keyi]){begin++;}Swap(&a[begin], &a[end]);}Swap(&a[keyi], &a[begin]);return begin;
}
挖坑法

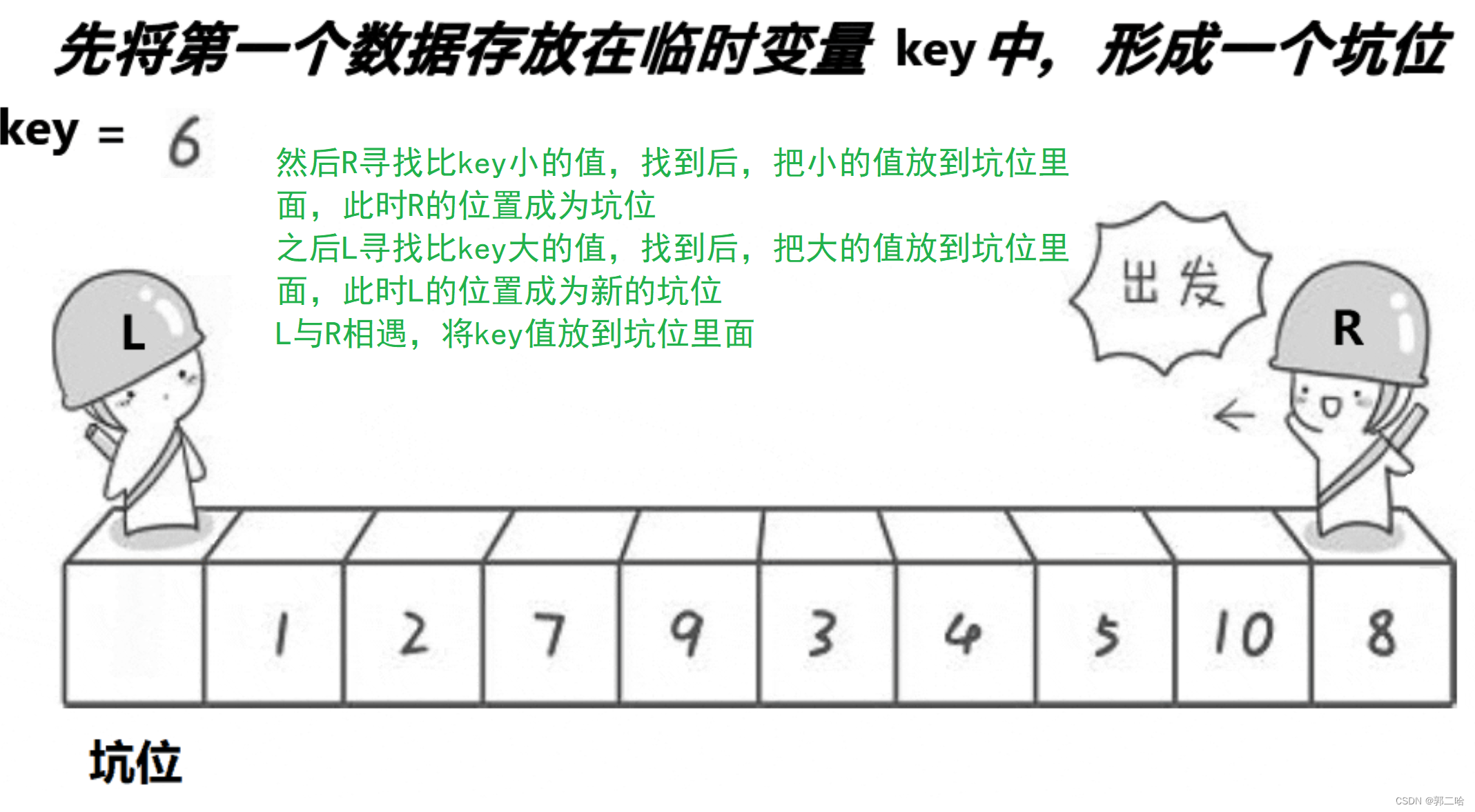
// 快速排序挖坑法
int PartSort2(int* a, int left, int right)
{//三数取中int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int key = a[left];int begin = left;int end = right;while (begin < end){while (begin < end && a[end] >= key){end--;}a[begin] = a[end];while (begin < end && a[begin] <= key){begin++;}a[end] = a[begin];}a[begin] = key;return begin;
}
前后指针


// 快速排序前后指针法
int PartSort3(int* a, int left, int right)
{//三数取中int midi = GetMidi(a, left, right);Swap(&a[left], &a[midi]);int keyi = left;int prev = left;int cur = prev + 1;while (cur <= right){if (a[cur] < a[keyi] && ++prev != cur){Swap(&a[cur], &a[prev]);}cur++;}Swap(&a[prev], &a[keyi]);return prev;
}
快排递归实现:
以上三种方法针对的是每一次排序,我们还需要递归剩下的区间来完成数据的有效
void QuickSort(int* a, int left, int right)
{//[left,right]是闭区间if (left >= right){return;}//小区间排序 -> 插入排序if ((right - left + 1) < 10){//注意数组取的位置和数组的长度InsertSort(a+left, right - left + 1);}else{//随便选择一种排序方法即可int keyi = PartSort3(a,left,right);//[left,keyi-1] keyi [keyi+1,right]//递归左边与右边QuickSort(a, left, keyi - 1);QuickSort(a, keyi + 1, right);}
}
在十万个数据下面,快速排序递归方法走了7ms,在一百万数据下面,走了80ms,可见效率非常快

快排非递归实现:
众所周知,递归会在栈上开辟空间,当递归的深度很大时,会导致栈溢出,这时我们可以把快速排序改成用非递归的形式实现
递归改为非递归的方法有两种:
- 用循环实现
- 利用栈来实现
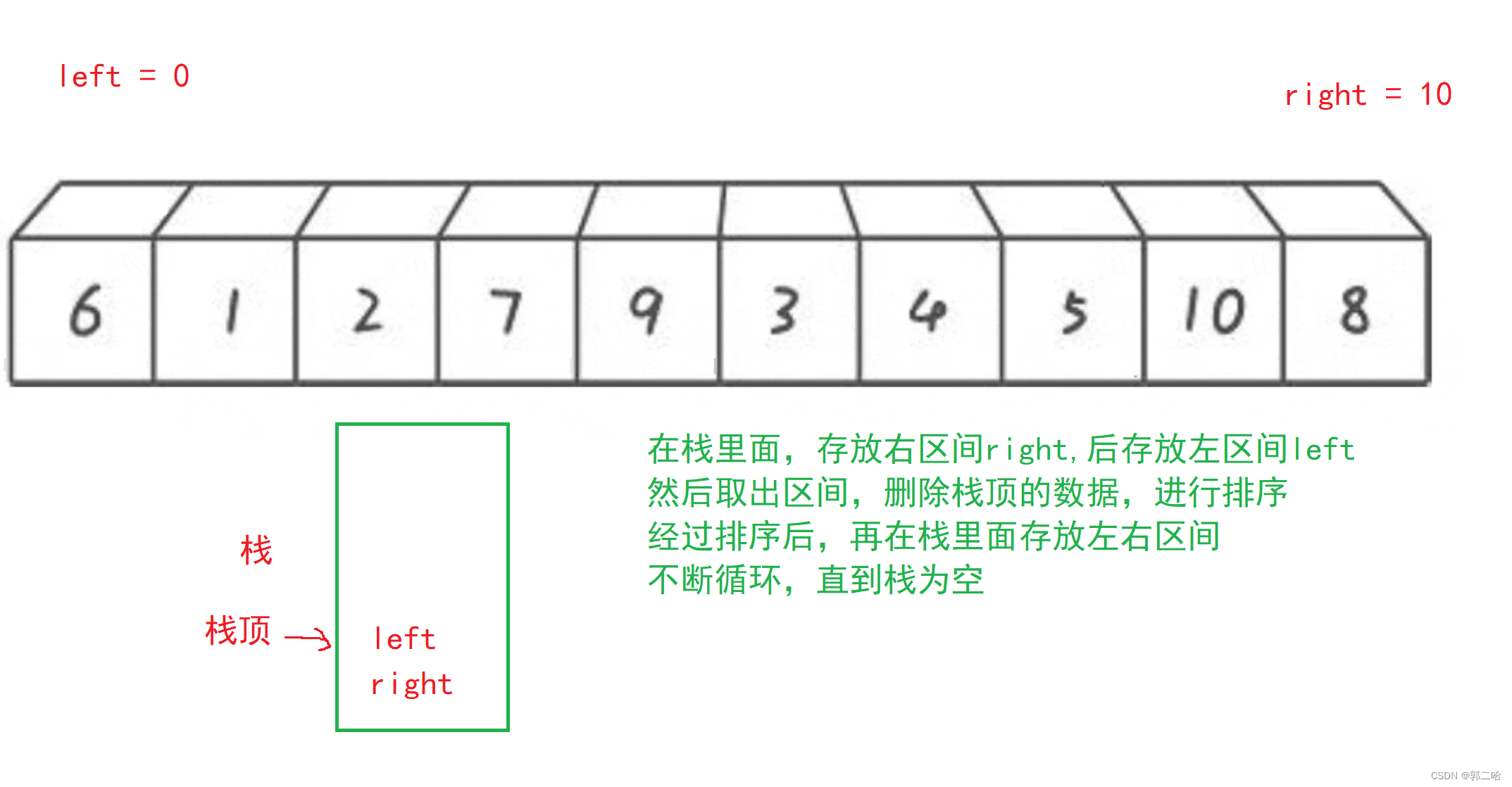
现在我们利用栈来实现,这里的栈是数据结构里面的栈。因为内存的栈的空间很小,而堆的空间很大,数据结构的栈就是在堆上开辟的
// 快速排序 非递归实现
//利用栈来实现
void QuickSortNonR(int* a, int left, int right)
{ST st;STInit(&st);STPush(&st, right);STPush(&st, left);while (!STEmpty(&st)){int begin = STTop(&st);STPop(&st);int end = STTop(&st);STPop(&st);int keyi = PartSort3(a, begin, end);//[begin,keyi-1] keyi [keyi+1,end]if (keyi + 1 < end){STPush(&st, end);STPush(&st, keyi + 1);}if (begin < keyi - 1){STPush(&st, keyi - 1);STPush(&st, begin);}}STDestroy(&st);
}
在十万个数据下面,快速排序非递归方法走了19ms,在一百万数据下面,走了283ms,可见效率与递归方法的差不多


七、归并排序
归并排序的时间复杂度是O(NlongN),空间复杂度是O(N),具有稳定性

归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide
andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并排序核心步骤:
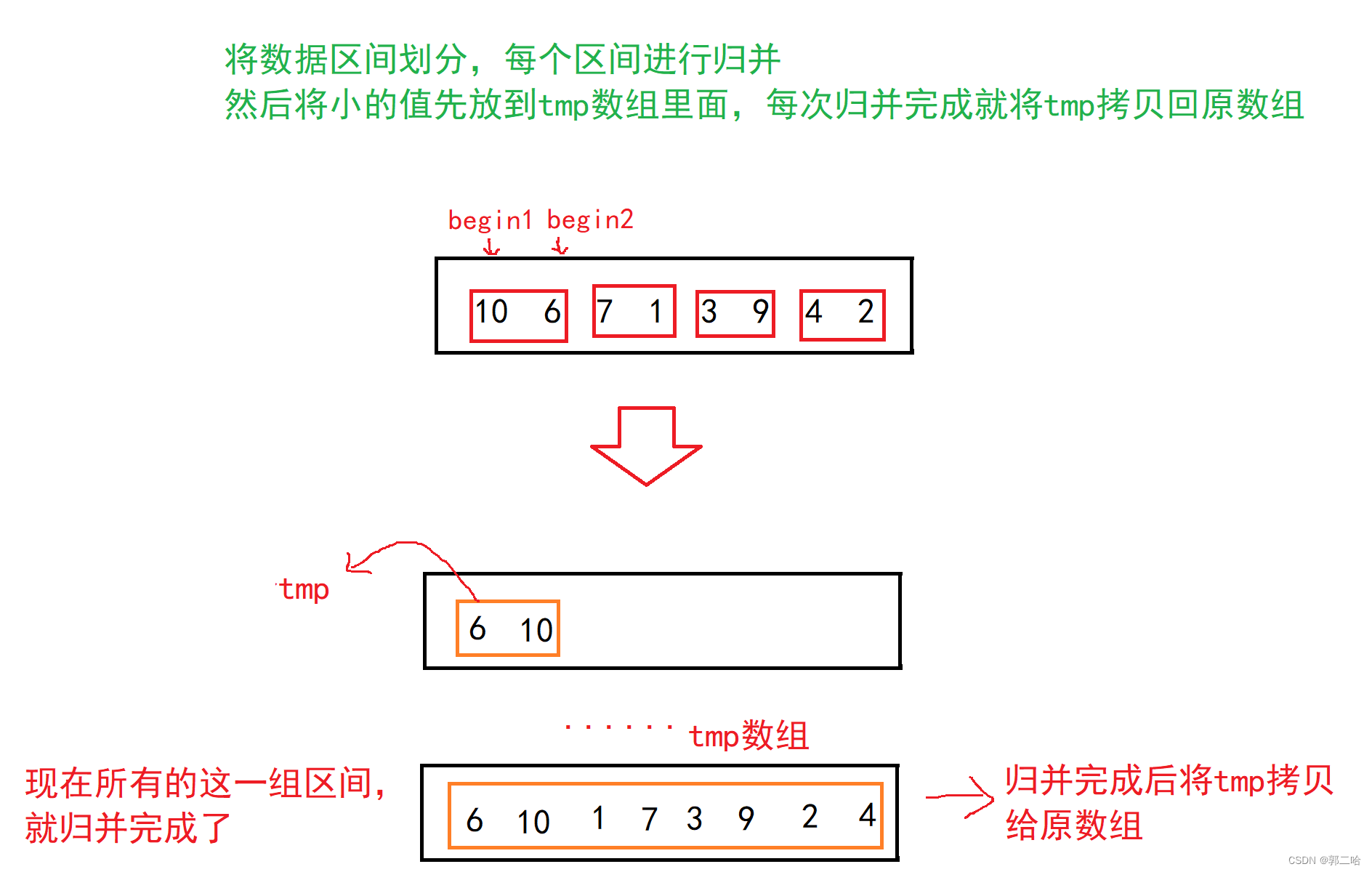
将数据划分区间,区间大小从小到大,每个区间进行归并,归并完成后就要拷贝回去
归并递归实现:
void _MergeSort(int* a, int* tmp, int left,int right)
{//递归if (left >= right){return;}int mid = (left + right) / 2;//[left,mid][mid+1,right]_MergeSort(a, tmp, left, mid);_MergeSort(a, tmp, mid+1, right);//归并int begin1 = left;int end1 = mid;int begin2 = mid + 1;int end2 = right;int i = left;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}//拷贝memcpy(a + left, tmp + left, (right - left + 1) * sizeof(int));
}//归并排序
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(n * sizeof(int));if (tmp == NULL){perror("malloc fail");return;}_MergeSort(a, tmp, 0, n - 1);free(tmp);tmp = NULL;
}
在十万个数据下面,归并排序递归方法走了9ms,在一百万数据下面,走了93ms,可见效率非常快

归并非递归实现:
上面我们提到递归会有栈溢出的问题,所有我们可以尝试一下归并的非递归的实现方法
递归改为非递归的方法有两种:
- 用循环实现
- 利用栈来实现
这次我们使用循环来实现,归并的核心就是分区间进行排序,既然如此, 我们可以设置分组gap的初始值为1,然后归并一次,归并完成后gap乘以2,来进行下一次的归并区间,不断重复此步骤直到gap 大于等于 数组长度时退出循环
//归并排序 非递归实现
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}//分组排序 每次两个gap组进行归并排序int gap = 1;while (gap < n){for (int i = 0; i < n; i+=2*gap){int begin1 = i;int end1 = i + gap - 1;int begin2 = i + gap;int end2 = i + 2 * gap - 1;int j = i;//printf("[%d,%d],[%d,%d]", begin1, end1, begin2, end2);//如果begin2越界了,就不归并if (begin2 >= n){break;}//如果end2越界了,就修正if (end2 >= n){end2 = n - 1;}//归并排序while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}//拷贝memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));}gap *= 2;}free(tmp);tmp = NULL;
}
在十万个数据下面,归并排序非递归方法走了9ms,在一百万数据下面,走了87ms,可见效率非常快


八、各个排序的对比图
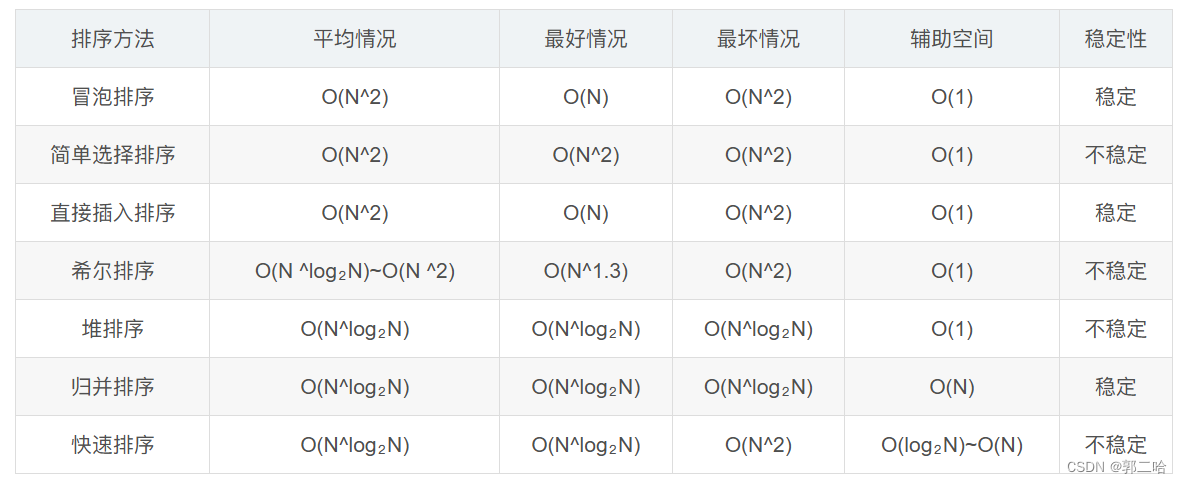
相关文章:

[数据结构】——七种常见排序
文章目录 前言 一.冒泡排序二.选择排序三.插入排序四.希尔排序五.堆排序六.快速排序hoare挖坑法前后指针快排递归实现:快排非递归实现: 七、归并排序归并递归实现:归并非递归实现: 八、各个排序的对比图 前言 排序:所谓…...

CPU占用率飙升至100%:是攻击还是正常现象?
在运维和开发的日常工作中,CPU占用率突然飙升至100%往往是一个令人紧张的信号。这可能意味着服务器正在遭受攻击,但也可能是由于某些正常的、但资源密集型的任务或进程造成的。本文将探讨如何识别和应对服务器的异常CPU占用情况,并通过Python…...

java如何替换字符串中给定索引的字符
java如果要修改给定字符串的索引字符,需要用到setCharAt方法 它的语法格式是 sbf.setCharAt(index,ch) 其中: sbf是任意StringBuffer对象 index是被替换字符的索引 ch是替换后的索引 如果是修改一个字符就用这个方法。如果是批量修改,…...
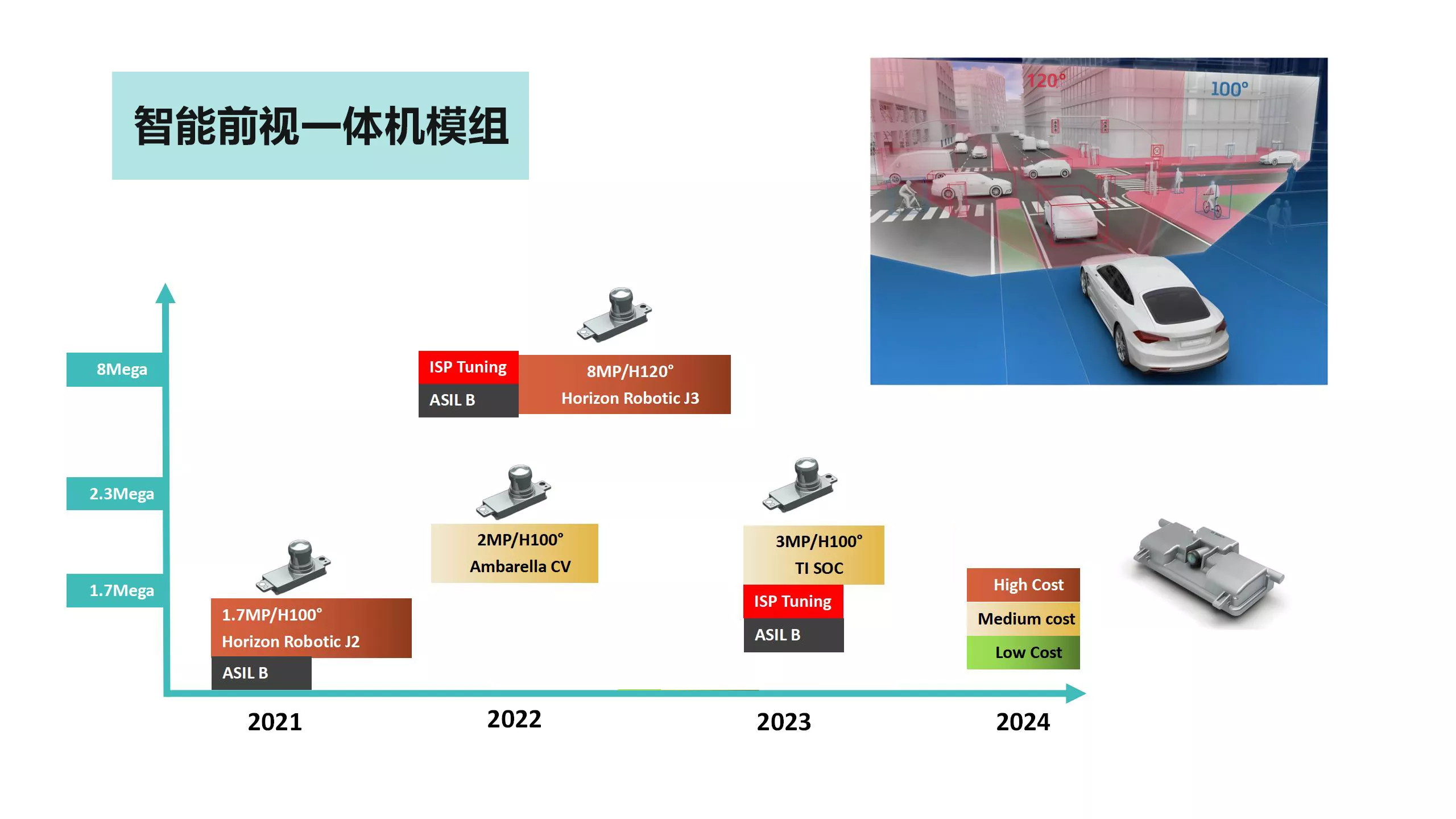
基于RK3588的GMSL、FPDLink 、VByone及MIPI等多种摄像模组,适用于车载、机器人工业图像识别领域
机器人&工业摄像头 针对机器人视觉与工业检测视觉,信迈自主研发和生产GMSL、FPDLink 、VByone及MIPI等多种摄像模组,并为不同应用场景提供多种视场角度和镜头。拥有资深的图像算法和图像ISP专家团队,能够在软件驱动层开发、ISP算法、FPG…...

Windows 的 MFC开发的使用示例——讲得挺好的
【Visual Studio 2019】创建 MFC 桌面程序 ( 安装 MFC 开发组件 | 创建 MFC 应用 | MFC 应用窗口编辑 | 为按钮添加点击事件 | 修改按钮文字 | 打开应用 )-腾讯云开发者社区-腾讯云 (tencent.com)...

Spring4.3.x xml配置文件搜索和解析过程
###概述 这篇文章的研究不只是涉及到spring如何创建一个BeanDefinition对象,还涉及到spring如何加载文件、如何读取XML文件、以及我们在使用spring的时候如何扩展spring的配置。 spring在创建BeanFactory时会把xml配置文件和注解信息转换为一个个BeanDefinition对…...

网络爬虫(一)深度优先爬虫与广度优先爬虫
1. 深度优先爬虫:深度优先爬虫是一种以深度为优先的爬虫算法。它从一个起始点开始,先访问一个链接,然后再访问该链接下的链接,一直深入地访问直到无法再继续深入为止。然后回溯到上一个链接,再继续深入访问下一个未被访…...

JavaScript懒加载图像
懒加载图像是一种优化网页性能的技术,它将页面中的图像延迟加载,即在用户需要查看它们之前不会立即加载。这种技术通常用于处理大量或大尺寸图像的网页,特别是那些包含长页面或大量媒体内容的网站。 好处 **1. 加快页面加载速度:…...

Git指令
一 参考:https://zhuanlan.zhihu.com/p/389814854 1.clone远程仓库 git clone https://git.xiaojukeji.com/falcon-mg/dagger.git 2.增加当前子目录下所有更改过的文件至index git add . 3.提交并备注‘xxx’ git commit -m ‘xxx’ 4.显示本地分支 git branch 5.显…...
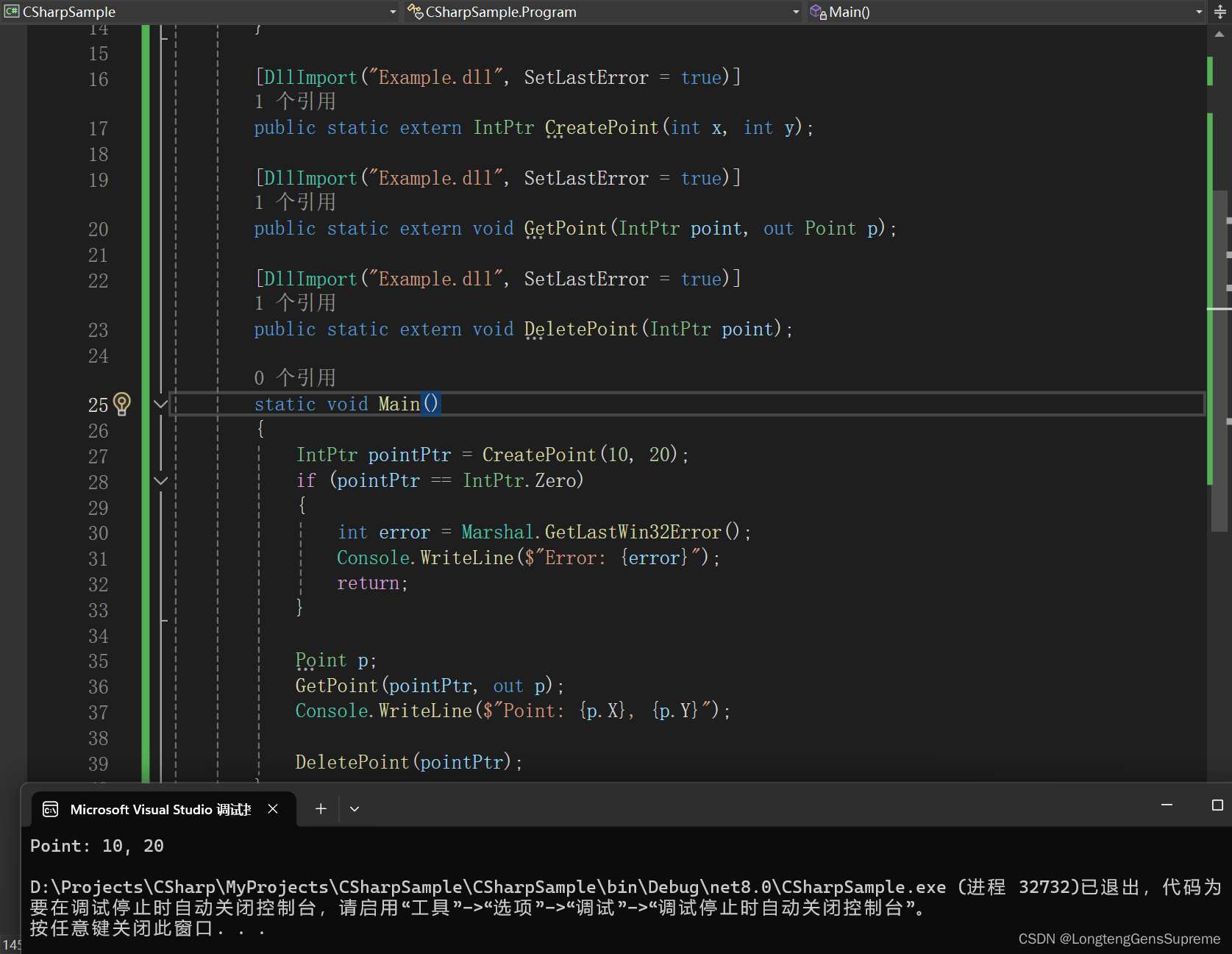
DllImport进阶:参数配置与高级主题探究
深入讨论DllImport属性的作用和配置方法 在基础篇中,我们已经简单介绍了DllImport的一些属性。现在我们将深入探讨这些属性的实际应用。 1. EntryPoint EntryPoint属性用于指定要调用的非托管函数的名称。如果托管代码中的函数名与非托管代码中的函数名不同&#…...

HTTP与HTTPS协议区别及应用场景
HTTP(超文本传输协议)和 HTTPS(安全超文本传输协议)都是用于通过网络传输数据的协议。虽然它们有一些相似之处,但在安全性和数据保护方面也存在显著差异。 在这篇博文中,我们将探讨 HTTP 和 HTTPS…...
Vue2-Vue Router前端路由实现思路
1.路由是什么? Router路由器:数据包转发设备,路由器通过转发数据包(数据分组)来实现网络互连 Route路由:数据分组从源到目的地时,决定端到端路径的网络范围的进程 | - 网络层 Distribute分发…...

2024 年 亚太赛 APMCM (C题)中文赛道国际大学生数学建模挑战赛 | 量子计算的物流配送 | 数学建模完整代码+建模过程全解全析
当大家面临着复杂的数学建模问题时,你是否曾经感到茫然无措?作为2022年美国大学生数学建模比赛的O奖得主,我为大家提供了一套优秀的解题思路,让你轻松应对各种难题! 完整内容可以在文章末尾领取! 该段文字…...

客观分析-自己和本科学生之间的差距
进入专科学校和与985、211等重点本科院校学生之间的差距可能由多种因素造成,这些因素可能包括但不限于: 1. **入学标准**: 985和211工程院校通常有更高的入学标准和更严格的选拔过程。 你得使你自己适应更高的入学标准和更严格的选拔过程&am…...

清华镜像源
python在安装各种库的时候为了下载速度快,经常使用镜像源,下面是使用清华镜像源案例。其中的 xxx 表示要安装的库,如 requests。 pip install xxx -i https://pypi.tuna.tsinghua.edu.cn/simple 安装requests案例:pip install r…...

大语言模型测评工具-ChatHub和ChatAll
背景 现在国内外拥有上百个大语言模型,在AI业务中,我们需要在其中选择一个合适业务模型,就需要对这些模型进行测试。手工去测试这么多模型效率一定不高,今天就介绍两个提高测评模型效率的工具 ChatHub和ChatAll。 介绍 ChatHub…...

使用redis分布式锁,不要把锁放在本地事务内部
在使用分布式锁的时候,习惯性的尽量缩小同步代码块的范围。 但是如果数据库隔离级别是可重复读,这种情况下不要把分布式锁加在Transactional注解的事务方法内部。 因为可能会出现这种情况: 线程1开启事务A后获取分布式锁,执行业务代码后在事务内释放了分布式锁。…...

Python学生信息管理系统(完整代码)
引言:(假装不是一个大学生课设)在现代教育管理中,学生管理系统显得尤为重要。这种系统能够帮助教育机构有效地管理学生资料、成绩、出勤以及其他教育相关活动,从而提高管理效率并减少人为错误。通过使用Python…...
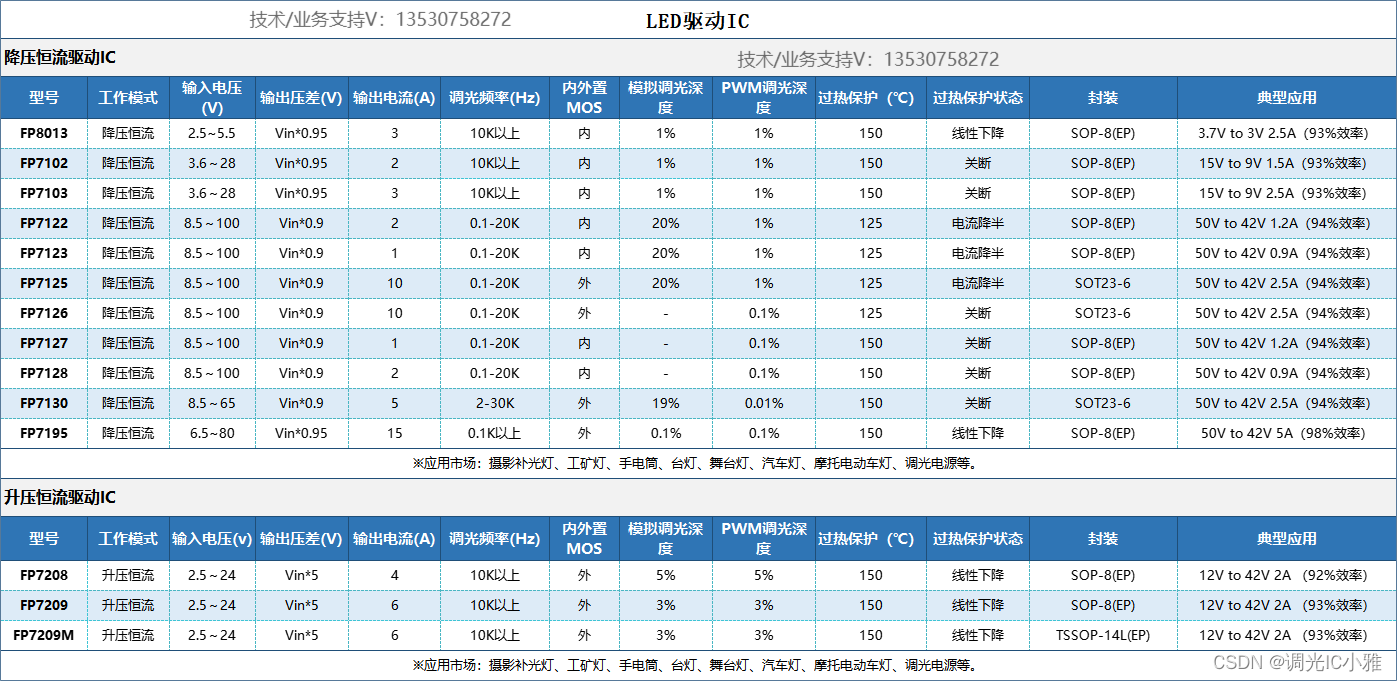
【大功率汽车大灯升压方案】LED恒流驱动芯片FP7208升压车灯调光应用,PWM内部转模拟,调光深度1%,无频闪顾虑,低亮无抖动
文章目录 前言 一、LED车灯的内部组成结构 二、驱动板详解 三、FP7208芯片介绍 芯片参数 总结 前言 近年来,汽车市场飞速发展,车灯作为汽车重要的组成部分,也得到了广泛的关注。车灯对于汽车不仅是外观件更是汽车主动安全的重要组成部…...

uniapp应用如何实现传感器数据采集和分析
UniApp是一种跨平台的应用开发框架,它支持在同一份代码中同时开发iOS、Android、H5等多个平台的应用。在UniApp中实现传感器数据采集和分析的过程可以分为以下几个步骤: 引入相关插件或库 UniApp通过插件或库的形式扩展功能。对于传感器数据采集和分析&…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
