动态规划 剪绳子问题
给一段长度为n的绳子,请把绳子剪成m段,每段绳子的长度为k[0],k[1],k[2],k[3]....k[m].请问k[0]k[1]k[2].....*k[m]的最大乘积为多少
#include <vector> // 包含vector头文件
#include <algorithm> // 包含algorithm头文件,用于max函数class Solution { // 定义解决方案类
public:int cutRope(int n) { // 主函数,计算最大乘积if (n <= 1) return 0; // 如果绳子长度小于等于1,无法剪断if (n == 2) return 1; // 如果绳子长度为2,最大乘积为1if (n == 3) return 2; // 如果绳子长度为3,最大乘积为2std::vector<int> dp(n + 1, 0); // 创建动态规划数组,初始化为0// 初始化基础情况dp[0] = 0; // 长度为0的绳子乘积为0dp[1] = 1; // 长度为1的绳子乘积为1dp[2] = 2; // 长度为2的绳子乘积为2dp[3] = 3; // 长度为3的绳子乘积为3for (int i = 4; i <= n; i++) { // 从长度4开始计算for (int j = 1; j <= i / 2; j++) { // 尝试所有可能的切割点dp[i] = std::max(dp[i], dp[j] * dp[i - j]); // 更新最大乘积}}return dp[n]; // 返回长度为n的绳子的最大乘积}
};这个实现使用了动态规划的方法来解决问题。以下是主要的设计思路:
- 我们定义了一个
Solution类,其中包含一个cutRope函数来解决这个问题。 - 首先,我们处理了一些特殊情况:
- 如果绳子长度小于等于1,无法剪断,返回0。
- 如果绳子长度为2,最大乘积为1(必须剪断)。
- 如果绳子长度为3,最大乘积为2(必须剪断)。
- 我们创建了一个动态规划数组
dp,其中dp[i]表示长度为i的绳子能得到的最大乘积。 - 初始化基础情况:
dp[0] = 0,dp[1] = 1,dp[2] = 2,dp[3] = 3- 注意,对于长度为2和3的情况,虽然必须剪断,但在作为子问题时,保持完整可能会得到更大的乘积。
- 然后,我们从长度4开始,逐步计算到长度n:
- 对于每个长度i,我们尝试所有可能的切割点j。
- 计算
dp[j] * dp[i-j],这代表将绳子切割成长度为j和i-j的两段。 - 使用
std::max函数来更新dp[i],保证它始终是最大的乘积。
- 最后,返回
dp[n],即为所求的最大乘积。
这个算法的时间复杂度为O(n^2),空间复杂度为O(n)。
当然可以使用更有效的解法,但是需要一点数学知识这个优化的算法基于一个数学发现:当绳子长度大于3时,尽可能多地切出长度为3的片段会得到最大乘积。如果最后剩下的长度为1,我们应该将其与一个3合并,形成一个长度为4的片段
class Solution { // 定义解决方案类
public:int cutRope(int n) { // 主函数,计算最大乘积if (n <= 3) return n - 1; // 处理特殊情况int quotient = n / 3; // 计算可以切出多少个长度为3的片段int remainder = n % 3; // 计算切完长度为3的片段后剩余的长度if (remainder == 0) { // 如果刚好被3整除return pow(3, quotient); // 返回3的quotient次方} else if (remainder == 1) { // 如果余1return pow(3, quotient - 1) * 4; // 最后的3和1合并为4} else { // 如果余2return pow(3, quotient) * 2; // 最后剩一个2}}private:int pow(int base, int exponent) { // 快速幂函数int result = 1; // 初始化结果为1while (exponent > 0) { // 当指数大于0时循环if (exponent & 1) { // 如果指数的二进制表示中当前位为1result *= base; // 将base乘到结果中}base *= base; // base自乘exponent >>= 1; // 指数右移一位}return result; // 返回结果}
};相关文章:

动态规划 剪绳子问题
给一段长度为n的绳子,请把绳子剪成m段,每段绳子的长度为k[0],k[1],k[2],k[3]....k[m].请问k[0]k[1]k[2].....*k[m]的最大乘积为多少 #include <vector> // 包含vector头文件 #include <algorithm> // 包含algorithm头文件,用于m…...
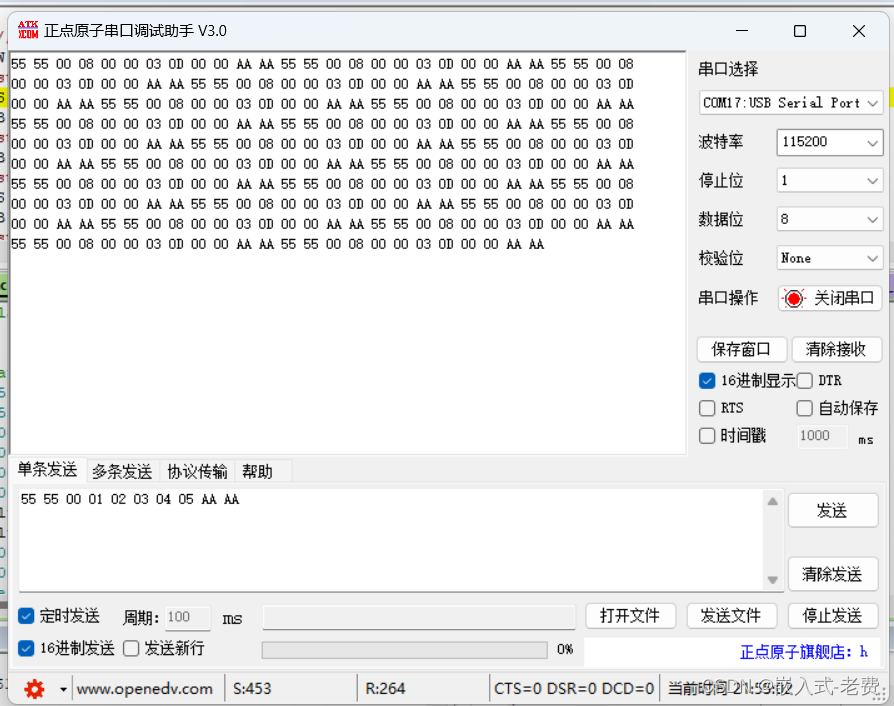
上位机图像处理和嵌入式模块部署(mcu项目1:实现协议)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 这种mcu的嵌入式模块理论上都是私有协议,因为上位机和下位机都是自己开发的,所以只需要自己保证上、下位机可以通讯上&…...
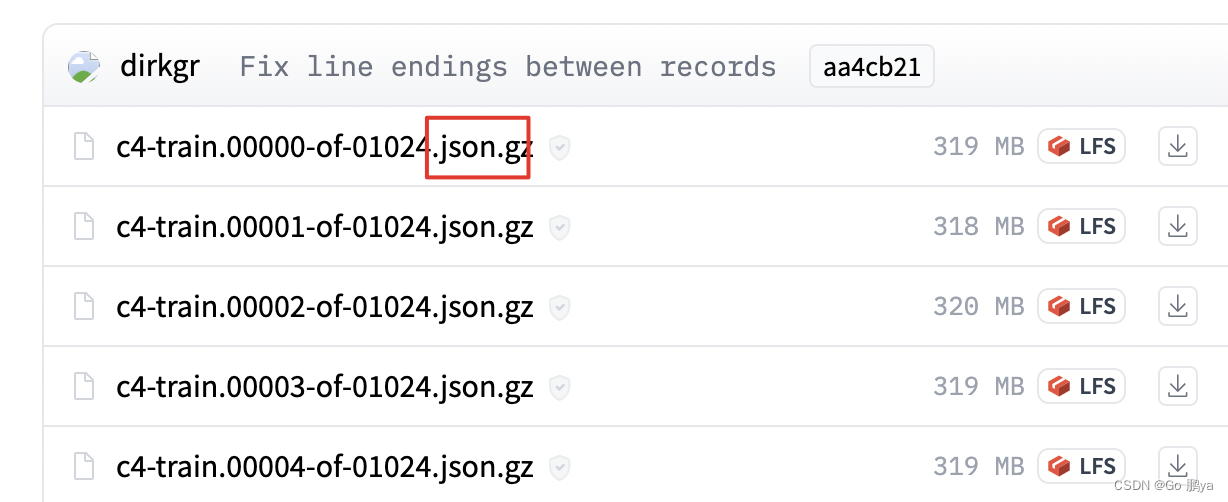
【NLP学习笔记】load_dataset加载数据
除了常见的load_dataset(<hf上的dataset名>)这种方式加载HF上的所有数据外,还有其他custom的选项。 加载HF上部分数据 from datasets import load_dataset c4_subset load_dataset("allenai/c4", data_files"en/c4-train.0000*-of-01024.js…...

企业如何选择好用的供应商管理系统
供应商管理系统软件(SRM)是企业用于管理供应链中各个供应商关系的重要工具。现如今竞争激烈的市场环境下,选择一款合适的SRM软件显得尤为重要。那么,如何选择一款好用的供应商管理系统呢? 企业在选择好用的供应商管理…...

震惊!运气竟能如此放大!运气的惊人作用,你了解吗?
芒格:得到你想要的东西,最保险的办法,就是让自己配得上你想要的那个东西。今天仔细想了想这句话,他其实说的是无数成功人士的心声 —— “我配得上!” 美剧《绝命毒师》有个导演叫文斯吉里根(Vince Gilliga…...

记录一次Apache Tomcat 处理返回自定义的404页面
记录工作中遇到处理访问tomcat 不存在的资源,返回自定义的404页面 删除webapps目录下的example、docs、manager、hta-manager目录,只保留 ROOT目录,应用部署在了这个目录 删除 manager、hta-manager 我没有发现有什么异常 制作404.jsp 或者 4…...

【piania 的用法】
piania 的用法 定义store建议使用箭头函数TypeScript插件扩展1、全局添加对象 定义store import { ref, computed } from vue import { defineStore } from pinia // pinia 以函数的形式暴露出去 export const useCounterStore defineStore(counter, () > {// 1、ref 相当…...
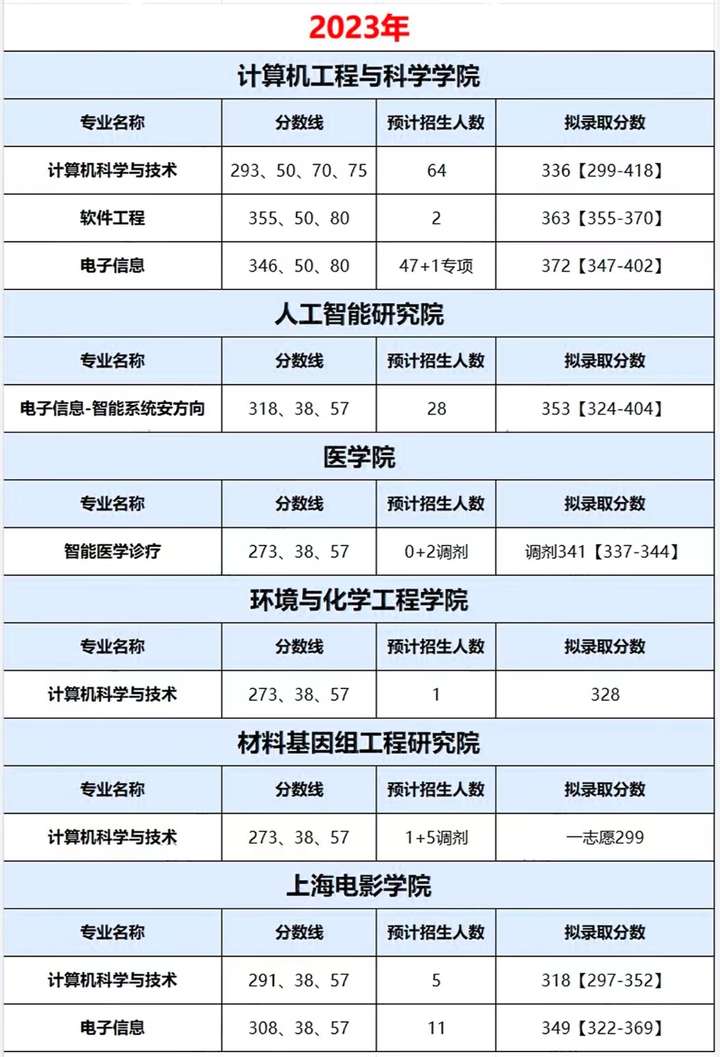
上海计算机考研炸了,这所学校慎报!上海大学计算机考研考情分析!
上海大学(Shanghai University),简称“上大”,是上海市属、国家“211工程”重点建设的综合性大学,教育部与上海市人民政府共建高校,国防科技工业局与上海市人民政府共建高校,国家“双一流”世界…...

面对全球新能源汽车合作发展创维汽车如何实现共赢
由全球新能源汽车合作组织(筹)主办、中国电动汽车百人会承办的首届全球新能源汽车合作发展论坛(GNEV2024)于6月27日,6月28日在新加坡金沙会议展览中心召开。创维汽车国际营销公司总经理齐奎源受邀参会并作出分享。 本届大会以推动全球新能源汽车产业协同发展与合作…...
对称加密和非对称加密以及相应算法)
安全和加密常识(1)对称加密和非对称加密以及相应算法
文章目录 对称加密(Symmetric Encryption)非对称加密(Asymmetric Encryption)使用场景和优缺点对称加密和非对称加密是信息安全领域中两种重要的加密方式,它们分别使用不同的加密算法和密钥管理方式来保护数据的机密性。下面我来简单介绍一下它们及其相应的算法。 对称加…...

afrog-漏洞扫描(挖洞)工具【了解安装使用详细】
★★免责声明★★ 文章中涉及的程序(方法)可能带有攻击性,仅供安全研究与学习之用,读者将信息做其他用途,由Ta承担全部法律及连带责任,文章作者不承担任何法律及连带责任。 1、afrog介绍 afrog 是一款性能卓越、快速稳定、PoC可定…...

c++类模板--无法解析的外部符号
解决办法 文章目录 解决办法方法1(推荐).在主函数包含头文件时将实现模板类的函数也包含进来方法2.将模板类的实现方法写在头文件里面方法3.函数模板声明前加inline 可能错误2,类内实现友元输出重载 方法1(推荐).在主函数包含头文件时将实现模板类的函数也包含进来 …...

Postman介绍
Postman 是一款流行的 API 开发和测试工具,它提供了一个直观的用户界面,使开发者可以轻松地构建、测试和修改 HTTP 请求。Postman 不仅适用于测试人员,也广泛应用于开发人员、产品经理和API设计者中,以确保API的正确性和性能。 以…...
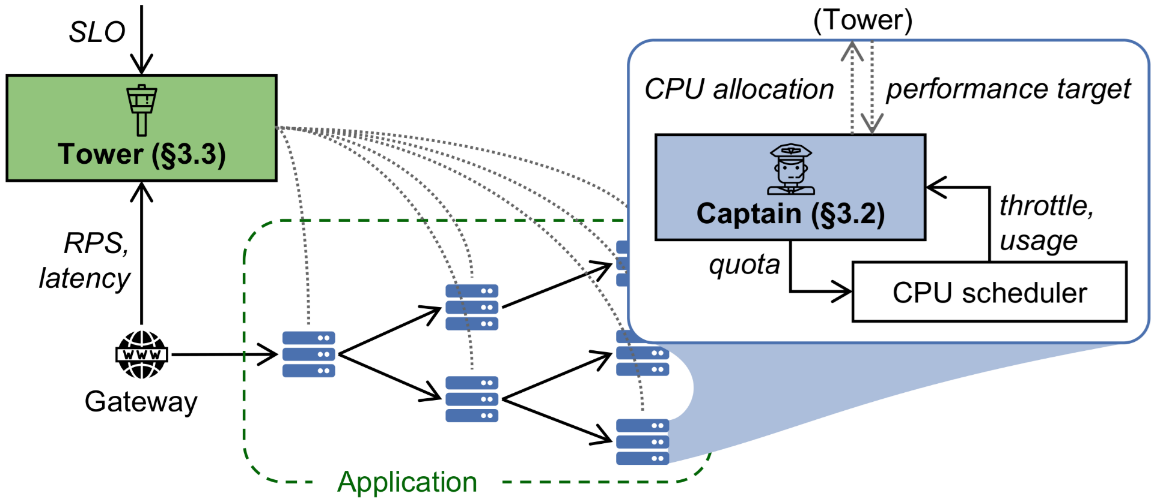
以智能化为舵手,引领现代计算机系统架构新航向
编者按:如今计算机系统承载的服务和算法逻辑日益复杂,理解、设计并改进计算机系统已成为核心挑战。面对系统复杂度和规模的指数级增长,以及新的大模型驱动场景下的分布式系统形态的涌现,人们亟需创新方法与技术来应对。在计算机系…...

揭秘品牌成功秘诀:品牌营销策略的核心要素大公开
品牌营销作为企业战略中至关重要的一环,其核心是建立和传播品牌的独特魅力,使其在消费者心目中占据重要位置。 一个成功的品牌营销策略能够提升品牌的知名度和影响力,带来持续的销售和忠诚客户群体。 在当今竞争激烈的市场环境中࿰…...

java如何把list转换成map
不废话,直接上代码 public static void main(String[] args) {List<UserxVO> list new ArrayList<>();for (int i 0; i < 10; i) {list.add(new UserxVO("n" i, "dd" i));}Map<String, String> map list.stream().co…...

vite typescript 配置跨域代理
打开工程目录下vite.config.ts文件 export default defineConfig({plugins: [vue(), topLevelAwait()],resolve: { alias },server:{proxy:{/api:{ //对以 /api 开头的请求跨域处理target:http://xxx.xxx.cn,//目标服务器changeOrigin: true,rewrite:(path)>{return path.…...
编辑 10 捕捉)
ArcGIS Pro SDK (七)编辑 10 捕捉
ArcGIS Pro SDK (七)编辑 10 捕捉 文章目录 ArcGIS Pro SDK (七)编辑 10 捕捉1 配置捕捉 - 打开或关闭捕捉2 配置捕捉 - 应用程序捕捉模式3 配置捕捉 - 图层捕捉可捕捉性4 配置捕捉 - 图层捕捉模式5 配置捕捉 - 组合示例6 捕捉选项…...
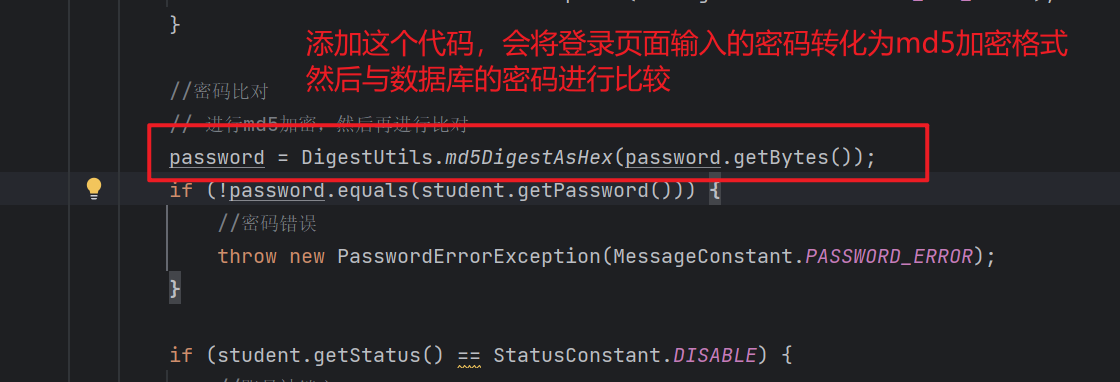
开始尝试从0写一个项目--后端(一)
创建文件的目录结构 利用这个界面创建 序号 名称 说明 1 SEMS maven父工程,统一管理依赖版本,聚合其他子模块 2 sems-common 子模块,存放公共类,例如:工具类、常量类、异常类等 3 sems-pojo 子模块&#x…...
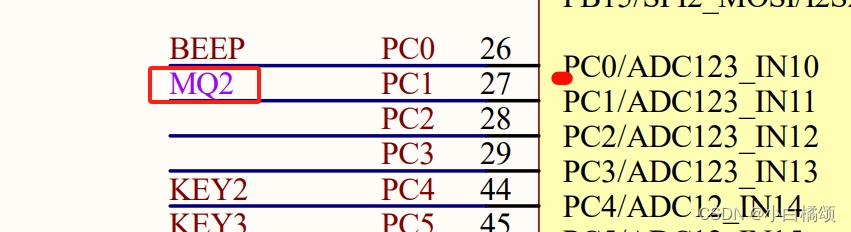
STM32第十二课:ADC检测烟雾浓度(MQ2)
文章目录 需求一、MQ-2 气体传感器特点应用电路及引脚 二、实现流程1.开时钟,分频,配IO2.配置ADC的工作模式3.配置通道4.复位,AD校准5.数值的获取 需求实现总结 需求 使用ADC将MQ2模块检测到的烟雾浓度模拟量转化为数字量。 最后,…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...
