机器人控制系列教程之Delta机器人动力学分析
动力学简介
机器人动力学分析是已知各运动构件的尺寸参数和惯性参数的情况下,求解末端运动状态与主驱动力矩之间的函数关系。
意义:对并联机器人动力学分析的意义体现在:
- 为伺服电机的选型提供理论依据;
- 获得动力学参数为目标函数的最优问题做性能评价指标;
- 为高精度控制提供基本的前提。
建模方法
在进行串联机器人的动力学分析时,我们讲过了凯恩法、拉格朗日法和牛顿-欧拉法,并对后两种方法进行了详细的阐述(详见第21讲)。而并联机器人的动力学建模相对于串联机器人较为复杂,但具体的建模过程差距不大。除此之外还有Hamliton原理法、虚功原理法等等。其中虚功原理的方法计算相对简单,效率相对较高,可以在后续的工作中加以适当的简化,进一步降低运算时间,使其满足实时控制的需要。
虚功原理法: 该方法运用到并联机器人动力学建模中较多,其主要的建模原理是:满足理想约束的刚体在系统上作用任何的平衡力,当刚体发生无穷小位移,则主动力在虚位移上做总功恒等于零。
Delta机器人雅可比矩阵
机器人机构的雅克比矩阵是一个变换矩阵,建立关节速度与操作空间速度的关系,它能够反映出机器人运动构件的能量传递。Delta机器人雅可比矩阵的数学关系式为:

通常情况下求解雅克比矩阵有微分法和矢量积法。Delta 机器人求解雅克比矩阵采用上述两种方法求解均可计算出,矢量法的求解已经在上上节讲述过,本节将采用微分法获得雅克比矩阵的解析式。由运动学建模中: ∣ B i P i ∣ = L a \left| {{B_i}{P_i}} \right| = {L_a} ∣BiPi∣=La
[ ( R − r + L a cos θ i ) cos η i − x ] 2 + [ ( R − r + L a cos θ i ) sin η i − y ] 2 + ( L a sin θ i + z ) 2 = L b 2 {\left[ {\left( {R - r + {L_a}\cos {\theta _i}} \right)\cos {\eta _i} - x} \right]^2} + {\left[ {\left( {R - r + {L_a}\cos {\theta _i}} \right)\sin {\eta _i} - y} \right]^2} + {\left( {{L_a}\sin {\theta _i} + z} \right)^2} = L_b^2 [(R−r+Lacosθi)cosηi−x]2+[(R−r+Lacosθi)sinηi−y]2+(Lasinθi+z)2=Lb2
将上式转化成隐式方程 f ( i ) f\left( i \right) f(i),i=1、2、3,对其求微分可得:

Delta机器人质量惯性矩阵
机器人的质量惯性矩阵可由机构的动能来获取,如某一刚体的动能和多刚体的动能可表示为:
T i = 1 2 ( m i v i T v i + ω i T I i ω i ) ⇒ T = ∑ i = 1 n T i {T_i} = {1 \over 2}\left( {{m_i}v_i^T{v_i} + \omega _i^T{I_i}{\omega _i}} \right) \Rightarrow T = \sum\limits_{i = 1}^n {{T_i}} Ti=21(miviTvi
相关文章:

机器人控制系列教程之Delta机器人动力学分析
动力学简介 机器人动力学分析是已知各运动构件的尺寸参数和惯性参数的情况下,求解末端运动状态与主驱动力矩之间的函数关系。 意义:对并联机器人动力学分析的意义体现在: 为伺服电机的选型提供理论依据;获得动力学参数为目标函数的最优问题做性能评价指标;为高精度控制提…...

VIM介绍
VIM(Vi IMproved)是一种高度可配置的文本编辑器,用于有效地创建和更改任何类型的文本。它是从 vi 编辑器发展而来的,后者最初是 UNIX 系统上的一个文本编辑器。VIM 以其键盘驱动的界面和强大的文本处理能力而闻名,是许…...
课设:选课管理系统(Java+MySQL)
在本博客中,我将介绍用Java、MySQL、JDBC和Swing GUI开发一个简单的选课管理系统。 技术栈 Java:用于编写应用程序逻辑MySQL:用于存储和管理数据JDBC:用于连接Java应用程序和MySQL数据库Swing GUI:用于构建桌面应用程…...

动态规划 剪绳子问题
给一段长度为n的绳子,请把绳子剪成m段,每段绳子的长度为k[0],k[1],k[2],k[3]....k[m].请问k[0]k[1]k[2].....*k[m]的最大乘积为多少 #include <vector> // 包含vector头文件 #include <algorithm> // 包含algorithm头文件,用于m…...
上位机图像处理和嵌入式模块部署(mcu项目1:实现协议)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 这种mcu的嵌入式模块理论上都是私有协议,因为上位机和下位机都是自己开发的,所以只需要自己保证上、下位机可以通讯上&…...
【NLP学习笔记】load_dataset加载数据
除了常见的load_dataset(<hf上的dataset名>)这种方式加载HF上的所有数据外,还有其他custom的选项。 加载HF上部分数据 from datasets import load_dataset c4_subset load_dataset("allenai/c4", data_files"en/c4-train.0000*-of-01024.js…...

企业如何选择好用的供应商管理系统
供应商管理系统软件(SRM)是企业用于管理供应链中各个供应商关系的重要工具。现如今竞争激烈的市场环境下,选择一款合适的SRM软件显得尤为重要。那么,如何选择一款好用的供应商管理系统呢? 企业在选择好用的供应商管理…...

震惊!运气竟能如此放大!运气的惊人作用,你了解吗?
芒格:得到你想要的东西,最保险的办法,就是让自己配得上你想要的那个东西。今天仔细想了想这句话,他其实说的是无数成功人士的心声 —— “我配得上!” 美剧《绝命毒师》有个导演叫文斯吉里根(Vince Gilliga…...

记录一次Apache Tomcat 处理返回自定义的404页面
记录工作中遇到处理访问tomcat 不存在的资源,返回自定义的404页面 删除webapps目录下的example、docs、manager、hta-manager目录,只保留 ROOT目录,应用部署在了这个目录 删除 manager、hta-manager 我没有发现有什么异常 制作404.jsp 或者 4…...

【piania 的用法】
piania 的用法 定义store建议使用箭头函数TypeScript插件扩展1、全局添加对象 定义store import { ref, computed } from vue import { defineStore } from pinia // pinia 以函数的形式暴露出去 export const useCounterStore defineStore(counter, () > {// 1、ref 相当…...
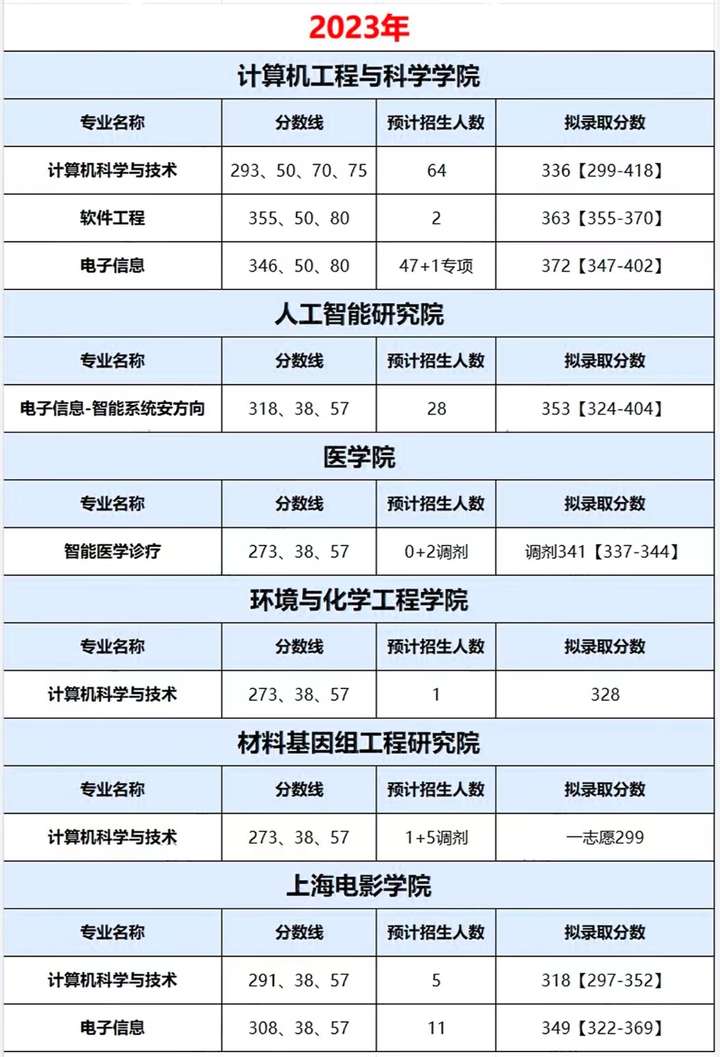
上海计算机考研炸了,这所学校慎报!上海大学计算机考研考情分析!
上海大学(Shanghai University),简称“上大”,是上海市属、国家“211工程”重点建设的综合性大学,教育部与上海市人民政府共建高校,国防科技工业局与上海市人民政府共建高校,国家“双一流”世界…...

面对全球新能源汽车合作发展创维汽车如何实现共赢
由全球新能源汽车合作组织(筹)主办、中国电动汽车百人会承办的首届全球新能源汽车合作发展论坛(GNEV2024)于6月27日,6月28日在新加坡金沙会议展览中心召开。创维汽车国际营销公司总经理齐奎源受邀参会并作出分享。 本届大会以推动全球新能源汽车产业协同发展与合作…...
对称加密和非对称加密以及相应算法)
安全和加密常识(1)对称加密和非对称加密以及相应算法
文章目录 对称加密(Symmetric Encryption)非对称加密(Asymmetric Encryption)使用场景和优缺点对称加密和非对称加密是信息安全领域中两种重要的加密方式,它们分别使用不同的加密算法和密钥管理方式来保护数据的机密性。下面我来简单介绍一下它们及其相应的算法。 对称加…...

afrog-漏洞扫描(挖洞)工具【了解安装使用详细】
★★免责声明★★ 文章中涉及的程序(方法)可能带有攻击性,仅供安全研究与学习之用,读者将信息做其他用途,由Ta承担全部法律及连带责任,文章作者不承担任何法律及连带责任。 1、afrog介绍 afrog 是一款性能卓越、快速稳定、PoC可定…...

c++类模板--无法解析的外部符号
解决办法 文章目录 解决办法方法1(推荐).在主函数包含头文件时将实现模板类的函数也包含进来方法2.将模板类的实现方法写在头文件里面方法3.函数模板声明前加inline 可能错误2,类内实现友元输出重载 方法1(推荐).在主函数包含头文件时将实现模板类的函数也包含进来 …...

Postman介绍
Postman 是一款流行的 API 开发和测试工具,它提供了一个直观的用户界面,使开发者可以轻松地构建、测试和修改 HTTP 请求。Postman 不仅适用于测试人员,也广泛应用于开发人员、产品经理和API设计者中,以确保API的正确性和性能。 以…...
以智能化为舵手,引领现代计算机系统架构新航向
编者按:如今计算机系统承载的服务和算法逻辑日益复杂,理解、设计并改进计算机系统已成为核心挑战。面对系统复杂度和规模的指数级增长,以及新的大模型驱动场景下的分布式系统形态的涌现,人们亟需创新方法与技术来应对。在计算机系…...

揭秘品牌成功秘诀:品牌营销策略的核心要素大公开
品牌营销作为企业战略中至关重要的一环,其核心是建立和传播品牌的独特魅力,使其在消费者心目中占据重要位置。 一个成功的品牌营销策略能够提升品牌的知名度和影响力,带来持续的销售和忠诚客户群体。 在当今竞争激烈的市场环境中࿰…...

java如何把list转换成map
不废话,直接上代码 public static void main(String[] args) {List<UserxVO> list new ArrayList<>();for (int i 0; i < 10; i) {list.add(new UserxVO("n" i, "dd" i));}Map<String, String> map list.stream().co…...

vite typescript 配置跨域代理
打开工程目录下vite.config.ts文件 export default defineConfig({plugins: [vue(), topLevelAwait()],resolve: { alias },server:{proxy:{/api:{ //对以 /api 开头的请求跨域处理target:http://xxx.xxx.cn,//目标服务器changeOrigin: true,rewrite:(path)>{return path.…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
