【算法】(C语言):堆排序
堆(二叉树的应用):
- 完全二叉树。
- 最大堆:每个节点比子树所有节点的数值都大,根节点是最大值。
- 父子索引号关系(根节点为0):(向上)子节点x,父节点(x-1) // 2。(向下)父节点x,左子节点2x+1,右子节点2x+2。
- 一般用数组实现堆。
堆排序:
第一步、构建堆(最大堆)。
- 找到最后的父节点:(最后元素的索引号-1) // 2。
- 从最后的父节点到根节点,依次向下调整(比较父节点和左右子节点,最大值为父节点)。
- 最终,根节点为最大值。尾指针指向最后节点。
第二步、排序
- 交换根节点和尾指针所在节点。此时,尾指针所在节点为目前正在排序中数据的最大值,保持不动。
- 尾指针向前(向左)移动一位。
- 从根节点到尾指针所在节点,依次向下调整。
- 此时,根节点为目前正在排序中数据的最大值(不包含已排序好且保持不动的最大值)。
第三步、重复第二步,直到尾指针指向根节点停止。
时间复杂度:O(nlogn)
- 初次构建堆,时间约n。
- 每次向下调整,都是使用2x+1、2x+2,遍历次数是logn(对数),几乎每个元素都要重排,因此时间约 nlogn。
- 相对于nlogn而言,n可忽略,即总时间O(nlogn)。
空间复杂度:O(1)
- 在原位置排序,只重复使用了用于交换的临时空间,不随数据量的变动而变动,空间使用为常量(1)。
C语言实现思路:
先构建堆(最大堆),再排序。
void heapsort(int *array, int length) // heap sort
{// 构建堆(最大堆)// 找到最后的父节点int i = ceil((length - 1) / 2); // 从最后的父节点到根节点,依次向下调整(父子节点比较大小,最大值为父节点)for(; i >= 0; i--){adjustdown(array, i, length - 1);}// 排序// 交换根节点和尾指针所在节点,尾指针前移一位,从根节点开始向下调整for(int n = length - 1; n > 0; n--){swap(&array[0], &array[n]);adjustdown(array, 0, n - 1);}
}因多次向下调整,多次交换两个数据,因此,向下调整、交换数据分别用函数单独实现。
交换两个数据:
传入的参数为数据的内存地址,将直接在内存地址进行数据交换。
void swap(int *a, int *b)
{int tmp = *a;*a = *b;*b = tmp;
}向下调整:
向下在左右子节点中找到较大值的节点,父节点再与较大值的子节点比较大小,若子节点数值更大,父子节点交换位置。
void adjustdown(int *array, int start, int end) // adjust the heap down
{while(start < end){int left = 2 * start + 1, right = 2 * start + 2, maxchild;// 比较左右子节点,找到较大值的子节点if(left > end) break;if(right <= end && array[left] < array[right]) maxchild = right;else maxchild = left;// 与较大值的子节点比较,若子节点数值更大,交换父子节点的位置if(array[start] < array[maxchild]){swap(&array[start], &array[maxchild]);start = maxchild;}else break;}
}完整代码:(heapsort.c)
#include <stdio.h>
#include <math.h>/* function prototype */
void heapsort(int *, int); // heap sort
void traverse(int *, int); // show element one by one/* main function */
int main(void)
{int arr[] = {4,2,6,9,5,1,3};int n = sizeof(arr) / sizeof(int);traverse(arr, n);heapsort(arr, n); printf("[ after heap sort ] ");traverse(arr, n);return 0;
}/* subfunction */
void swap(int *a, int *b) // change the value of two datas
{int tmp = *a;*a = *b;*b = tmp;
}void adjustdown(int *array, int start, int end) // adjust the heap down
{while(start < end){int left = 2 * start + 1, right = 2 * start + 2, maxchild;// left child or right child, find the max oneif(left > end) break;if(right <= end && array[left] < array[right]) maxchild = right;else maxchild = left;// parent compair with maxchild, if smaller than maxchild,change the positionif(array[start] < array[maxchild]){swap(&array[start], &array[maxchild]);start = maxchild;}else break;}
}void heapsort(int *array, int length) // heap sort
{// build a heapint i = ceil((length - 1) / 2); // find the last parent// from the last parent to 0 index, cycle ajust the heap down(parent compair with child)for(; i >= 0; i--){adjustdown(array, i, length - 1);}// sort (root is max, change max to the last, end pointer move a step to the left)for(int n = length - 1; n > 0; n--){// swap the first and last elementswap(&array[0], &array[n]);// from 0 index, compair with left child and right child, max is parentadjustdown(array, 0, n - 1);}
}void traverse(int *array, int length) // show element one by one
{printf("elements(%d): ", length);for(int k = 0; k < length; k++){printf("%d ", array[k]);}printf("\n");
}编译链接: gcc -o heapsort heapsort.c
执行可执行文件: ./heapsort

相关文章:

【算法】(C语言):堆排序
堆(二叉树的应用): 完全二叉树。最大堆:每个节点比子树所有节点的数值都大,根节点是最大值。父子索引号关系(根节点为0):(向上)子节点x,父节点(x…...
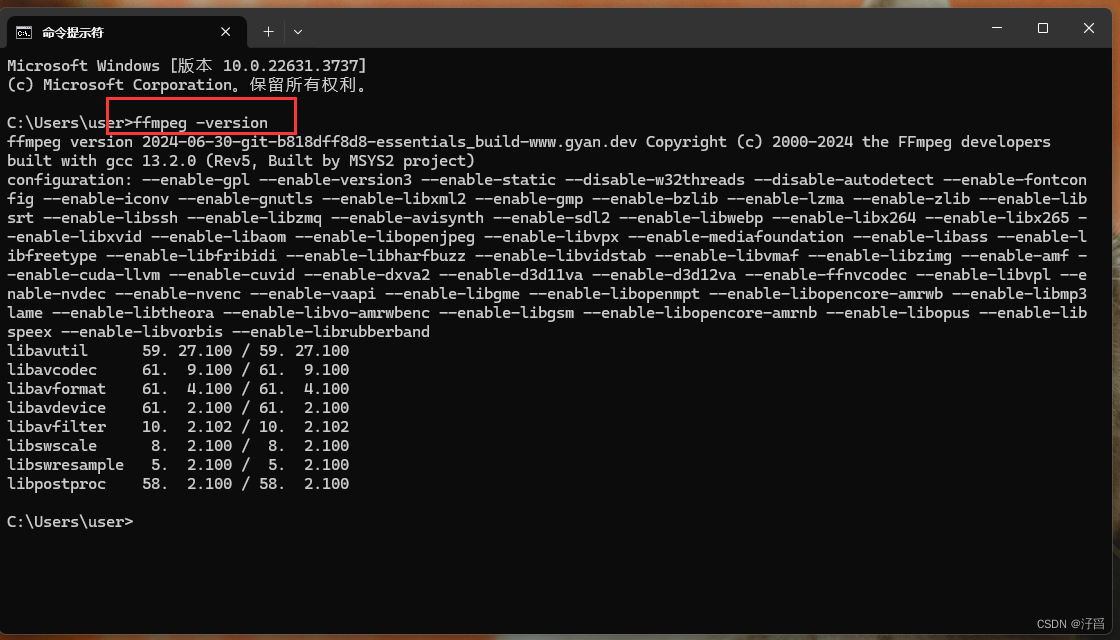
ffmpeg下载/配置环境/测试
一、下载 1、访问FFmpeg官方网站下载页面:FFmpeg Download Page; 2、选择适合Windows的版本(将鼠标移动到windows端)。通常,你会找到“Windows builds from gyan.dev”或者“BtbN GitHub Releases”等选项࿰…...
C# 异步编程详解(Task,async/await)
文章目录 1.什么是异步2.Task 产生背景3.Thread(线程) 和 Task(异步)的区别3.1 几个名词3.2 Thread 与 Task 的区别 4.Task API4.1 创建和启动任务4.2 Task 等待、延续和组合4.3 task.Result4.4 Task.Delay() 和 Thread.Sleep() 区别 5.CancellationToken 和 CancellationToken…...
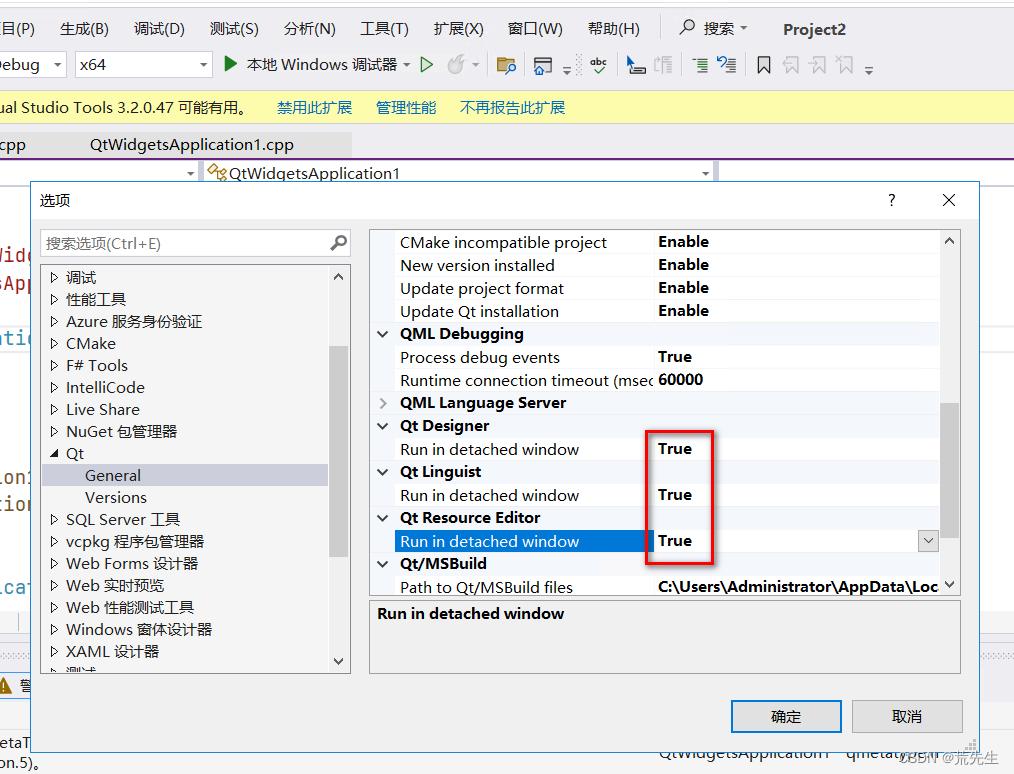
qt结合vs2022安装
进入清华大学开源软件: 清华大学开源软件镜像站 | Tsinghua Open Source Mirror 下载完成后,双击进行安装: 进入邮箱进行验证: 可能是因为网络问题,无法安装。 重新安装5.12.12版本。 安装后启动失败,重新…...

Kafka集群部署(手把手部署图文详细版)
1.1.1 部署zookpeer 在node02下载并解压zookeeper软件包 cd /usr/local wget https://archive.apache.org/dist/zookeeper/zookeeper-3.4.6/zookeeper-3.4.6.tar.gz 或者:scp cat192.168.28.100:/home/cat/zookeeper-3.4.6.tar.gz /tmp(注意目录…...

阿里Qwen2-72B大模型已是开源榜的王者,为什么还要推出其他参数模型,被其他模型打榜?
6 月 27 日,全球知名的开源平台 Hugging Face 的联合创始人兼首席执行官 Clem 在社交平台激动宣布,阿里 Qwen2-72B 成为了开源模型排行榜的王者。 这是一件大好事,说明了我们在大模型领域从先前的追赶,逐渐走向了领导,…...
7.基于SpringBoot的SSMP整合案例-表现层开发
目录 1.基于Restfu1进行表现层接口开发 1.1创建功能类 1.2基于Restful制作表现层接口 2.接收参数 2使用Apifox测试表现层接口功能 保存接口: 分页接口: 3.表现层一致性处理 3.1先创建一个工具类,用作后端返回格式统一类:…...

【server】3、注册中心与配置中心
1、服务注册与发现 1.1、consul 1.1.1 是什么 官网: Consul by HashiCorp spring-cloud-consul: Spring Cloud Consul :: Spring Cloud Consul gitHub 官网 :GitHub - hashicorp/consul: Consul is a distributed, highly available, and data cent…...

【大数据】—量化交易实战案例(海龟交易策略)
声明:股市有风险,投资需谨慎!本人没有系统学过金融知识,对股票有敬畏之心没有踏入其大门,今天用另外一种方法模拟炒股,后面的模拟的实战全部用同样的数据,最后比较哪种方法赚的钱多。 海龟交易…...

014-GeoGebra基础篇-快速解决滑动条的角度无法输入问题
有客户反馈,他的Geogebra一直有个bug,那就是输入角度最大值时总不按照他设定的展示,快被气炸了~ 目录 一、问题复现(1)插入一个滑动条(2)选择Angle(3)输入90,…...
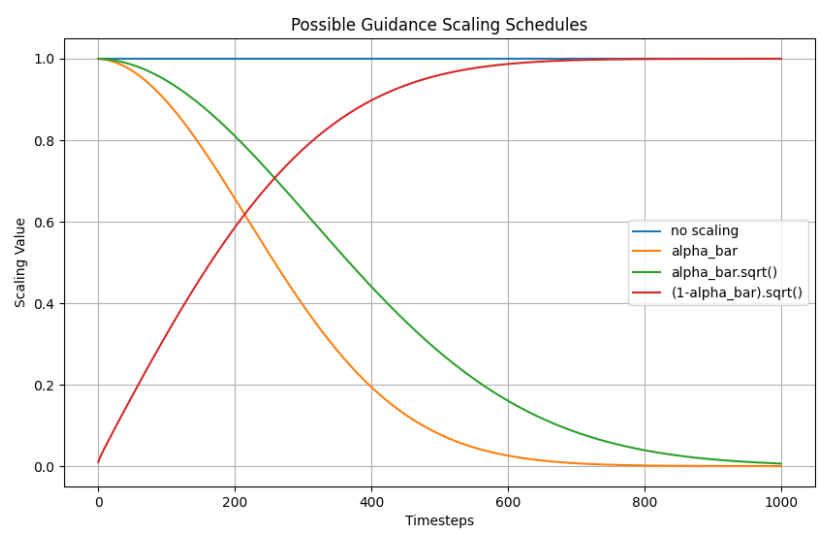
Diffusion模型的微调和引导
留意后续更新,欢迎关注微信公众号:组学之心 Diffusion模型的微调和引导 微调(fine-tuning): 从一个已经训练过的模型开始训练,我们就可以从一个学会如何“去噪”的模型开始训练,相对于随机初始…...

零基础学MySQL:从入门到实践的完整指南
引言: MySQL,作为全球最受欢迎的开源关系型数据库管理系统之一,以其高性能、易用性和灵活性,在Web开发、数据分析等领域占据着举足轻重的地位。如果你是一位编程新手,想要踏入数据库管理的大门,本文将从零…...

澳蓝荣耀时刻,6款产品入选2024年第一批《福州市名优产品目录》
近日,福州市工业和信息化局公布2024年第一批《福州市名优产品目录》,澳蓝自主研发生产的直接蒸发冷却空调、直接蒸发冷却组合式空调机组、间接蒸发冷水机组、高效间接蒸发冷却空调机、热泵式热回收型溶液调湿新风机组、防火湿帘6款产品成功入选。 以上新…...

Frrouting快速入门——OSPF组网(一)
FRR简介 FRR是FRRouting的简称,是一个开源的路由交换软件套件。其作者源自老牌项目quaga的成员,也可以算是quaga的新版本。 使用时一般查看此文档:https://docs.frrouting.org/projects/dev-guide/en/latest/index.html FRR支持的协议众多…...

记录通过Cloudflare部署属于自己的docker镜像源
引言 由于最近国内无法正常拉取docker镜像,然而找了几个能用的docker镜像源发现拉取回来的docker镜像不是最新的版本,部署到Cloudflare里Workers 和 Pages,拉取docker 镜像成功,故记录部署过程。 部署服务 登录Cloudflare后&…...

波动方程 - 在三维图中动态显示二维波动方程的解就像水面波澜起伏
波动方程 - 在三维图中动态显示二维波动方程的解就像水面波澜起伏 flyfish 波动方程的求解结果通常不是一个单一的数值,而是一个函数或一组函数,这些函数描述了波随时间和空间的传播情况。具体来说,波动方程的解可以是关于时间和空间变量的…...

yum命令提示 错误:rpmdb: BDB0113 Thread/process 4153/139708200269632
一、报错信息 [rootDawn yum.repos.d]# yum clean all 错误:rpmdb: BDB0113 Thread/process 4153/139708200269632 failed: BDB1507 Thread died in Berkeley DB library 错误:db5 错误(-30973) 来自 dbenv->failchk:BDB0087 DB_RUNRECOVE…...
欢乐钓鱼大师游戏攻略:在什么地方掉称号鱼?云手机游戏辅助!
《欢乐钓鱼大师》是一款融合了休闲娱乐和策略挑战的钓鱼游戏。游戏中的各种鱼类不仅各具特色,而且钓鱼过程充满了挑战和乐趣。下面将为大家详细介绍如何在游戏中钓鱼,以及一些有效的钓鱼技巧,帮助你成为一个出色的钓鱼大师。 实用工具推荐 为…...

什么是构造函数?Java 中构造函数的重载如何实现?
构造函数,就像是建筑房屋时的奠基仪式,是Java类中一个特殊的方法,主要用于初始化新创建的对象。 每当创建一个类的新实例时,构造函数就会自动调用,负责为这个新对象分配内存,并对其进行必要的设置…...

Linux内核 -- ARMv7 与 ARMv8 中的 asmlinkage 作用及使用
ARMv7 与 ARMv8 中的 asmlinkage 作用及使用 asmlinkage 是一个宏,通常在内核代码中使用,用于定义调用约定,特别是指定函数的参数是通过栈传递而不是通过寄存器。它主要用于内核与汇编之间的接口函数,使得参数传递更加一致和明确…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
