波动方程 - 在三维图中动态显示二维波动方程的解就像水面波澜起伏
波动方程 - 在三维图中动态显示二维波动方程的解就像水面波澜起伏
flyfish
波动方程的求解结果通常不是一个单一的数值,而是一个函数或一组函数,这些函数描述了波随时间和空间的传播情况。具体来说,波动方程的解可以是关于时间和空间变量的函数,表示在这些变量下波的振幅或位置。

二维波动方程
二维波动方程的形式为:
∂ 2 u ∂ t 2 = c 2 ( ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 ) \frac{\partial^2 u}{\partial t^2} = c^2 \left( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \right) ∂t2∂2u=c2(∂x2∂2u+∂y2∂2u)其中, u ( x , y , t ) u(x, y, t) u(x,y,t) 是时间 t t t 和空间 ( x , y ) (x, y) (x,y) 上的波函数, c c c 是波速。
差分公式
为了数值求解这个偏微分方程,我们可以将其离散化。离散化的过程中使用以下有限差分近似:
-
时间方向的二阶偏导数:
∂ 2 u ∂ t 2 ≈ u i , j n + 1 − 2 u i , j n + u i , j n − 1 Δ t 2 \frac{\partial^2 u}{\partial t^2} \approx \frac{u^{n+1}_{i,j} - 2u^{n}_{i,j} + u^{n-1}_{i,j}}{\Delta t^2} ∂t2∂2u≈Δt2ui,jn+1−2ui,jn+ui,jn−1 -
空间 x x x 方向的二阶偏导数:
∂ 2 u ∂ x 2 ≈ u i + 1 , j n − 2 u i , j n + u i − 1 , j n Δ x 2 \frac{\partial^2 u}{\partial x^2} \approx \frac{u^{n}_{i+1,j} - 2u^{n}_{i,j} + u^{n}_{i-1,j}}{\Delta x^2} ∂x2∂2u≈Δx2ui+1,jn−2ui,jn+ui−1,jn -
空间 y y y 方向的二阶偏导数:
∂ 2 u ∂ y 2 ≈ u i , j + 1 n − 2 u i , j n + u i , j − 1 n Δ y 2 \frac{\partial^2 u}{\partial y^2} \approx \frac{u^{n}_{i,j+1} - 2u^{n}_{i,j} + u^{n}_{i,j-1}}{\Delta y^2} ∂y2∂2u≈Δy2ui,j+1n−2ui,jn+ui,j−1n
将这些差分公式代入波动方程中,得到离散化的波动方程:
u i , j n + 1 − 2 u i , j n + u i , j n − 1 Δ t 2 = c 2 ( u i + 1 , j n − 2 u i , j n + u i − 1 , j n Δ x 2 + u i , j + 1 n − 2 u i , j n + u i , j − 1 n Δ y 2 ) \frac{u^{n+1}_{i,j} - 2u^{n}_{i,j} + u^{n-1}_{i,j}}{\Delta t^2} = c^2 \left( \frac{u^{n}_{i+1,j} - 2u^{n}_{i,j} + u^{n}_{i-1,j}}{\Delta x^2} + \frac{u^{n}_{i,j+1} - 2u^{n}_{i,j} + u^{n}_{i,j-1}}{\Delta y^2} \right) Δt2ui,jn+1−2ui,jn+ui,jn−1=c2(Δx2ui+1,jn−2ui,jn+ui−1,jn+Δy2ui,j+1n−2ui,jn+ui,j−1n)
整理得到显式更新公式:
u i , j n + 1 = 2 u i , j n − u i , j n − 1 + c 2 Δ t 2 ( u i + 1 , j n − 2 u i , j n + u i − 1 , j n Δ x 2 + u i , j + 1 n − 2 u i , j n + u i , j − 1 n Δ y 2 ) u^{n+1}_{i,j} = 2u^{n}_{i,j} - u^{n-1}_{i,j} + c^2 \Delta t^2 \left( \frac{u^{n}_{i+1,j} - 2u^{n}_{i,j} + u^{n}_{i-1,j}}{\Delta x^2} + \frac{u^{n}_{i,j+1} - 2u^{n}_{i,j} + u^{n}_{i,j-1}}{\Delta y^2} \right) ui,jn+1=2ui,jn−ui,jn−1+c2Δt2(Δx2ui+1,jn−2ui,jn+ui−1,jn+Δy2ui,j+1n−2ui,jn+ui,j−1n)
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.animation import FuncAnimation# 定义参数
t_max = 3 # 时间范围
x_max = 1 # 空间范围
y_max = 1
m = 320 # 时间方向的格子数
n = 32 # 空间 x 方向的格子数
k = 32 # 空间 y 方向的格子数# 时间和空间步长
dt = t_max / (m - 1)
dx = x_max / (n - 1)
dy = y_max / (k - 1)# 初始化解数组
u = np.zeros((m, n, k))# 设置初始条件
x_vals, y_vals = np.linspace(0, x_max, n), np.linspace(0, y_max, k)
X, Y = np.meshgrid(x_vals, y_vals)
u[0, :, :] = np.sin(4 * np.pi * X) + np.cos(4 * np.pi * Y)
u[1, :, :] = np.sin(4 * np.pi * X) + np.cos(4 * np.pi * Y)# 按照公式进行差分
for ii in range(1, m - 1):for jj in range(1, n - 1):for kk in range(1, k - 1):u[ii + 1, jj, kk] = (dt**2 * (u[ii, jj + 1, kk] + u[ii, jj - 1, kk] - 2 * u[ii, jj, kk]) / dx**2 +dt**2 * (u[ii, jj, kk + 1] + u[ii, jj, kk - 1] - 2 * u[ii, jj, kk]) / dy**2 +2 * u[ii, jj, kk] - u[ii - 1, jj, kk])# 创建图形
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_zlim(-4, 4)# 初始化图像
surf = ax.plot_surface(X, Y, u[0, :, :], cmap='viridis')def update(frame):ax.clear()ax.set_zlim(-4, 4)ax.set_title(f"Time step: {frame}")surf = ax.plot_surface(X, Y, u[frame, :, :], cmap='viridis')return surf,# 创建动画
ani = FuncAnimation(fig, update, frames=m, repeat=True)
ani.save('wave_quation.gif', writer='imagemagick')
plt.show()
相关文章:

波动方程 - 在三维图中动态显示二维波动方程的解就像水面波澜起伏
波动方程 - 在三维图中动态显示二维波动方程的解就像水面波澜起伏 flyfish 波动方程的求解结果通常不是一个单一的数值,而是一个函数或一组函数,这些函数描述了波随时间和空间的传播情况。具体来说,波动方程的解可以是关于时间和空间变量的…...

yum命令提示 错误:rpmdb: BDB0113 Thread/process 4153/139708200269632
一、报错信息 [rootDawn yum.repos.d]# yum clean all 错误:rpmdb: BDB0113 Thread/process 4153/139708200269632 failed: BDB1507 Thread died in Berkeley DB library 错误:db5 错误(-30973) 来自 dbenv->failchk:BDB0087 DB_RUNRECOVE…...
欢乐钓鱼大师游戏攻略:在什么地方掉称号鱼?云手机游戏辅助!
《欢乐钓鱼大师》是一款融合了休闲娱乐和策略挑战的钓鱼游戏。游戏中的各种鱼类不仅各具特色,而且钓鱼过程充满了挑战和乐趣。下面将为大家详细介绍如何在游戏中钓鱼,以及一些有效的钓鱼技巧,帮助你成为一个出色的钓鱼大师。 实用工具推荐 为…...

什么是构造函数?Java 中构造函数的重载如何实现?
构造函数,就像是建筑房屋时的奠基仪式,是Java类中一个特殊的方法,主要用于初始化新创建的对象。 每当创建一个类的新实例时,构造函数就会自动调用,负责为这个新对象分配内存,并对其进行必要的设置…...

Linux内核 -- ARMv7 与 ARMv8 中的 asmlinkage 作用及使用
ARMv7 与 ARMv8 中的 asmlinkage 作用及使用 asmlinkage 是一个宏,通常在内核代码中使用,用于定义调用约定,特别是指定函数的参数是通过栈传递而不是通过寄存器。它主要用于内核与汇编之间的接口函数,使得参数传递更加一致和明确…...

GPT提示词模板
BRTR 原则 # 背景(Background) - 描述任务的背景信息,包括任务的起因、目的、相关的历史信息或当前状况。 - 提供足够的背景信息以便让ChatGPT理解任务的上下文。 # 角色(Role) - 定义ChatGPT在任务中所扮演的角色&…...
WRF学习——使用CMIP6数据驱动WRF/基于ncl与vdo的CMIP6数据处理
动力降尺度 国际耦合模式比较计划(CMIP)为研究不同情景下的气候变化提供了大量的模拟数据,而在实际研究中,全球气候模式输出的数据空间分辨率往往较低(>100Km,缺乏区域气候特征,为了更好地研…...

机器人控制系列教程之Delta机器人动力学分析
动力学简介 机器人动力学分析是已知各运动构件的尺寸参数和惯性参数的情况下,求解末端运动状态与主驱动力矩之间的函数关系。 意义:对并联机器人动力学分析的意义体现在: 为伺服电机的选型提供理论依据;获得动力学参数为目标函数的最优问题做性能评价指标;为高精度控制提…...

VIM介绍
VIM(Vi IMproved)是一种高度可配置的文本编辑器,用于有效地创建和更改任何类型的文本。它是从 vi 编辑器发展而来的,后者最初是 UNIX 系统上的一个文本编辑器。VIM 以其键盘驱动的界面和强大的文本处理能力而闻名,是许…...
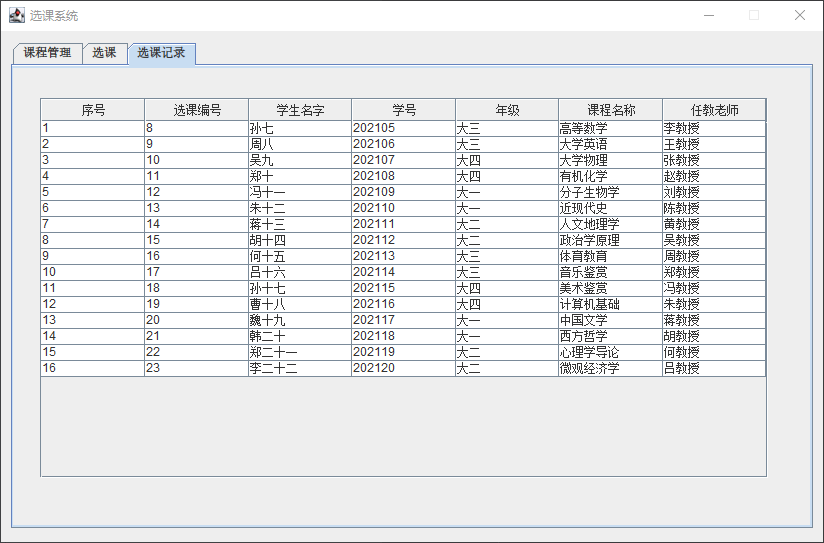
课设:选课管理系统(Java+MySQL)
在本博客中,我将介绍用Java、MySQL、JDBC和Swing GUI开发一个简单的选课管理系统。 技术栈 Java:用于编写应用程序逻辑MySQL:用于存储和管理数据JDBC:用于连接Java应用程序和MySQL数据库Swing GUI:用于构建桌面应用程…...

动态规划 剪绳子问题
给一段长度为n的绳子,请把绳子剪成m段,每段绳子的长度为k[0],k[1],k[2],k[3]....k[m].请问k[0]k[1]k[2].....*k[m]的最大乘积为多少 #include <vector> // 包含vector头文件 #include <algorithm> // 包含algorithm头文件,用于m…...
上位机图像处理和嵌入式模块部署(mcu项目1:实现协议)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 这种mcu的嵌入式模块理论上都是私有协议,因为上位机和下位机都是自己开发的,所以只需要自己保证上、下位机可以通讯上&…...
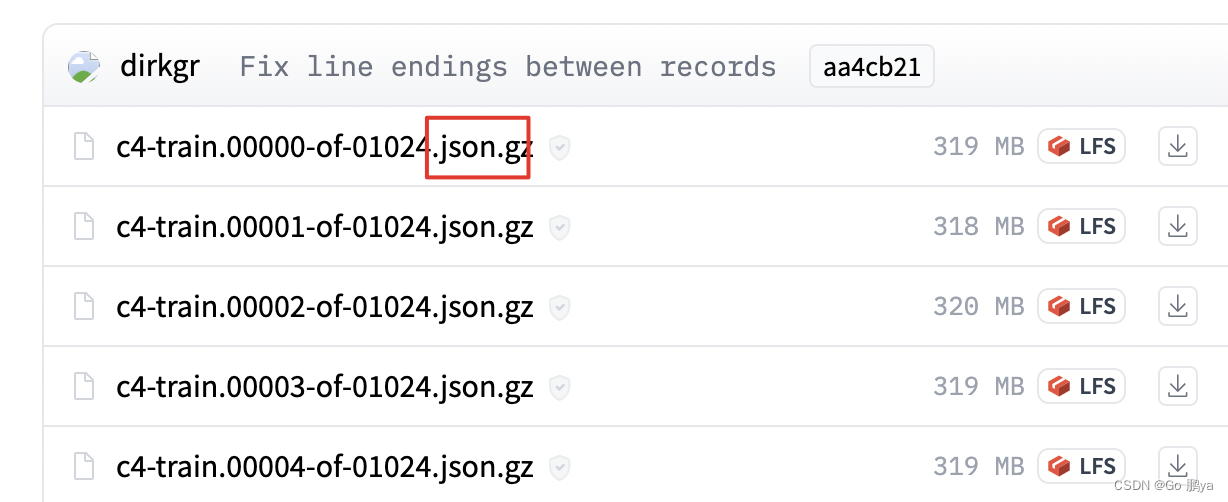
【NLP学习笔记】load_dataset加载数据
除了常见的load_dataset(<hf上的dataset名>)这种方式加载HF上的所有数据外,还有其他custom的选项。 加载HF上部分数据 from datasets import load_dataset c4_subset load_dataset("allenai/c4", data_files"en/c4-train.0000*-of-01024.js…...

企业如何选择好用的供应商管理系统
供应商管理系统软件(SRM)是企业用于管理供应链中各个供应商关系的重要工具。现如今竞争激烈的市场环境下,选择一款合适的SRM软件显得尤为重要。那么,如何选择一款好用的供应商管理系统呢? 企业在选择好用的供应商管理…...

震惊!运气竟能如此放大!运气的惊人作用,你了解吗?
芒格:得到你想要的东西,最保险的办法,就是让自己配得上你想要的那个东西。今天仔细想了想这句话,他其实说的是无数成功人士的心声 —— “我配得上!” 美剧《绝命毒师》有个导演叫文斯吉里根(Vince Gilliga…...

记录一次Apache Tomcat 处理返回自定义的404页面
记录工作中遇到处理访问tomcat 不存在的资源,返回自定义的404页面 删除webapps目录下的example、docs、manager、hta-manager目录,只保留 ROOT目录,应用部署在了这个目录 删除 manager、hta-manager 我没有发现有什么异常 制作404.jsp 或者 4…...

【piania 的用法】
piania 的用法 定义store建议使用箭头函数TypeScript插件扩展1、全局添加对象 定义store import { ref, computed } from vue import { defineStore } from pinia // pinia 以函数的形式暴露出去 export const useCounterStore defineStore(counter, () > {// 1、ref 相当…...
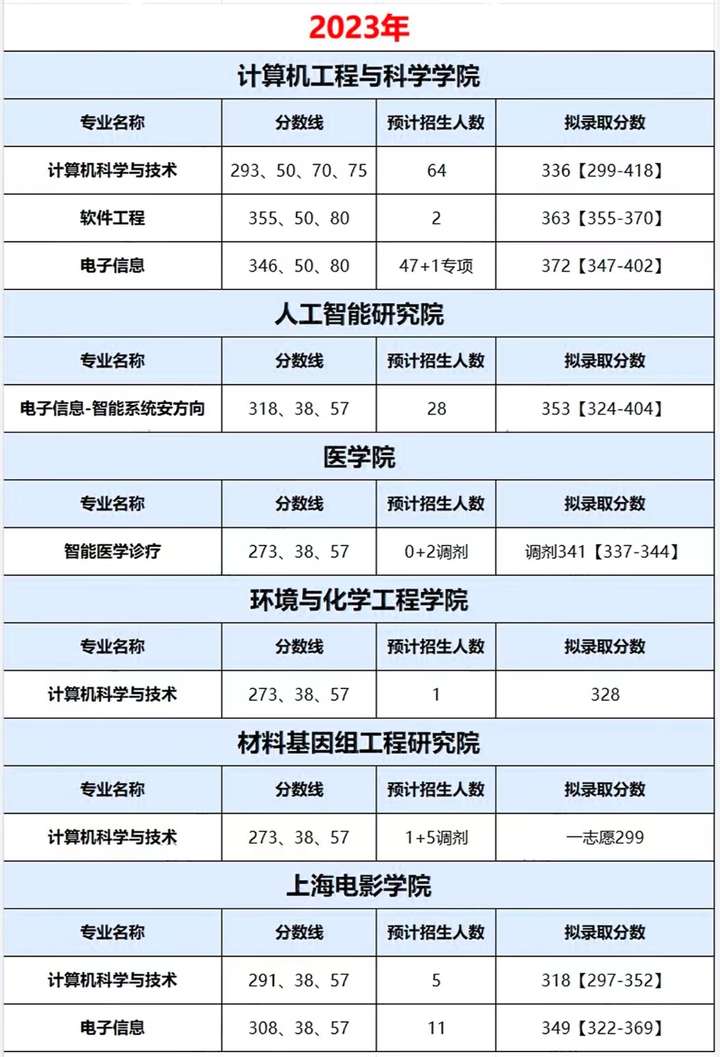
上海计算机考研炸了,这所学校慎报!上海大学计算机考研考情分析!
上海大学(Shanghai University),简称“上大”,是上海市属、国家“211工程”重点建设的综合性大学,教育部与上海市人民政府共建高校,国防科技工业局与上海市人民政府共建高校,国家“双一流”世界…...

面对全球新能源汽车合作发展创维汽车如何实现共赢
由全球新能源汽车合作组织(筹)主办、中国电动汽车百人会承办的首届全球新能源汽车合作发展论坛(GNEV2024)于6月27日,6月28日在新加坡金沙会议展览中心召开。创维汽车国际营销公司总经理齐奎源受邀参会并作出分享。 本届大会以推动全球新能源汽车产业协同发展与合作…...
对称加密和非对称加密以及相应算法)
安全和加密常识(1)对称加密和非对称加密以及相应算法
文章目录 对称加密(Symmetric Encryption)非对称加密(Asymmetric Encryption)使用场景和优缺点对称加密和非对称加密是信息安全领域中两种重要的加密方式,它们分别使用不同的加密算法和密钥管理方式来保护数据的机密性。下面我来简单介绍一下它们及其相应的算法。 对称加…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
