64.函数参数和指针变量
目录
一.函数参数
二.函数参数和指针变量
三.视频教程
一.函数参数
函数定义格式:
类型名 函数名(函数参数1,函数参数2...)
{代码段
}
如:
int sum(int x,int y)
{return x+y;
}函数参数的类型可以是普通类型,也可以是指针类型。什么时候使用指针类型呢?
二.函数参数和指针变量
例:
在主函数中有俩个整数并存入变量中,然后在被调函数中将这俩个变量的值互换。
如果不使用指针变量作为函数参数,我们这样写。
#include <stdio.h>void swap(int a,int b)
{int c;c = a;a = b;b = c;printf("a is %d,b is %d\n",a,b);
}int main(void)
{int a = 1;int b = 2;swap(a,b);printf("a is %d,b is %d\n",a,b);return 0;}运行结果:

a和b只在swap函数中被调换了。如果不使用指针变量,我们可以这样修改:
#include <stdio.h>int a = 1;
int b = 2;void swap(void)
{int c;c = a;a = b;b = c;printf("a is %d,b is %d\n",a,b);
}int main(void)
{swap();printf("a is %d,b is %d\n",a,b);return 0;}运行结果:

虽然成功实现了a和b值的互换,但是swap函数非常不灵活,只能交换a和b的值,基本上写死了。
如果我们使用指针变量作为参数会发生什么事情呢?
#include <stdio.h>void swap(int *a,int *b)
{int c;c = *a;*a = *b;*b = c;
}int main(void)
{int a = 1;int b = 2;swap(&a,&b);printf("a is %d,b is %d\n",a,b);return 0;}运行结果:

分析:
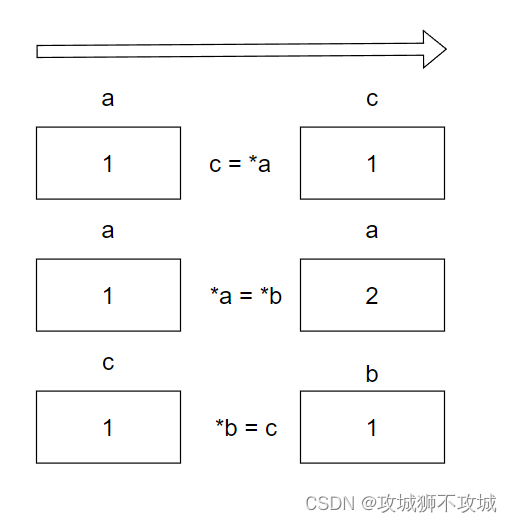
使用指针变量作为参数成功实现了a和b互换,而且swap函数非常灵活,可以在任意函数中调用。这个就是指针作为函数参数的意义。
三.视频教程
64.函数参数和指针变量_哔哩哔哩_bilibili
相关文章:

64.函数参数和指针变量
目录 一.函数参数 二.函数参数和指针变量 三.视频教程 一.函数参数 函数定义格式: 类型名 函数名(函数参数1,函数参数2...) {代码段 } 如: int sum(int x,int y) {return xy; } 函数参数的类型可以是普通类型,也可以是指针类…...
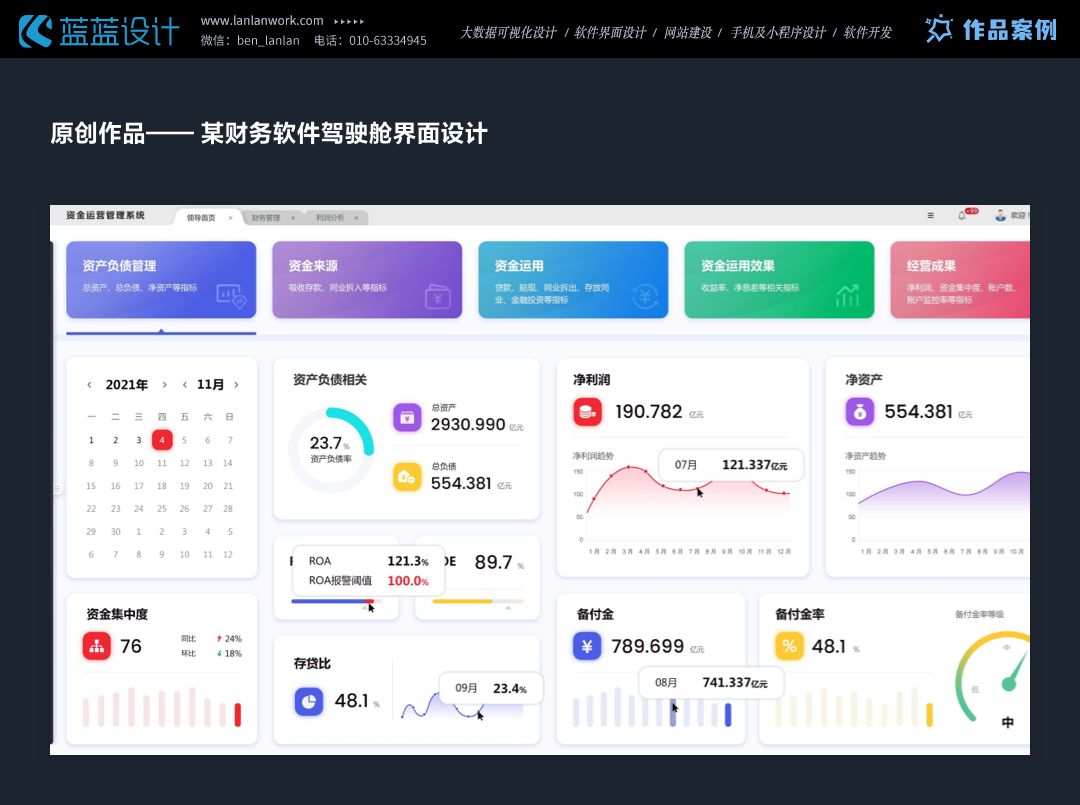
原创作品 —(金融行业)年金系统交互和视觉设计
金融行业软件交互设计要点:“简化操作流程,确保流畅易用,同时注重交易环境的安全可靠,通过个性化体验提升用户满意度,并及时收集反馈以持续优化。” 2.UI设计要点:“注重视觉效果与用户体验的平衡ÿ…...

3D slicer
...

面试题--SpringCloud
SpringCloud SOA 和微服务的区别?(必会) 谈到 SOA 和微服务的区别, 那咱们先谈谈架构的演变 1. 集中式架构 项目功能简单, 一个项目只需一个应用, 将所有功能部署在一起, 这样的架构好处是减 少了部署节点和成本. 缺点: 代码耦合,开发维护困难 2. 垂直拆分架构 …...

Qt windeployqt 打包的Qt动态库介绍
前言 在 Windows 平台,通常使用 Qt 的工具 windeployqt 将可执行文件的相关 Qt 依赖项部署到当前路径下。 Windows windeployqt 部署工具 Windows 部署工具 windeployqt 旨在自动化创建一个可部署文件夹的过程,该文件夹包含运行应用程序所需的 Qt 相关…...
WordPress付费进群V2主题,多种引流方法,引私域二次变现
全新前端UI界面,多种前端交互特效让页面不再单调,进群页面群成员数,群成员头像名称,每次刷新页面随机更新不重复,最下面评论和点赞也是如此随机刷新不重复 进群页面简介,群聊名称,群内展示&…...
:kmem、mem)
【Linux】性能分析器 perf 详解(三):kmem、mem
上一篇:【Linux】性能分析器 perf 详解(二) 1、perf kmem 1.1 简介 kmem 用于跟踪/测量内核内存属性的工具,如分配、释放、碎片率等。可以帮助开发者和系统管理员理解内核内存的分配和释放模式,从而诊断内存泄漏、过度分配等问题。 功能: 跟踪内存分配和释放:监控内…...

微信小程序怎样跳转页面?
在微信小程序中,页面跳转通常使用 wx.navigateTo、wx.redirectTo、wx.switchTab、wx.navigateBack 以及 wx.reLaunch 等API。这些API提供了不同的页面跳转方式,适用于不同的场景。 以下是这些API的详细代码示例和说明: 1.wx.navigateTo&…...

针对SVN、GIT版本管理工具进行源代码加密保护
针对SVN、GIT版本管理工具进行源代码加密保护 在软件开发过程中,版本管理工具如SVN和GIT是不可或缺的组成部分,它们帮助团队管理源代码的变更和版本。然而,这些工具也面临着源代码泄露的安全风险。如果不针对数据进行加密保护,很…...

js条件引用
在JavaScript中,条件引用模块通常涉及到在运行时根据条件判断来决定是否加载某个模块。这在某些情况下非常有用,比如在不同环境下使用不同的模块,或者在某些特定条件下才需要某个模块的功能。 以下是几种在JavaScript中实现条件引用的方法&a…...
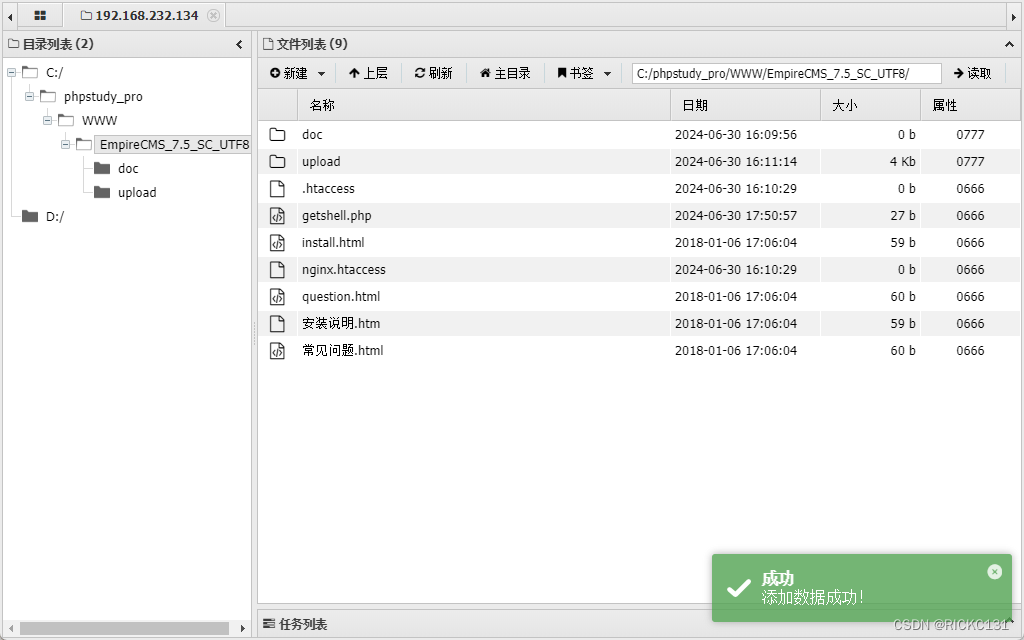
帝国CMS(EmpireCMS)漏洞复现
简介 《帝国网站管理系统》英文译为Empire CMS,简称Ecms,它是基于B/S结构,且功能强大而帝国CMS-logo易用的网站管理系统。 帝国CMS官网:http://www.phome.net/ 参考相关漏洞分析文章,加上更详细的渗透测试过程。 参考…...
DP:解决路径问题
文章目录 二维DP模型如何解决路径问题有关路径问题的几个问题1.不同路径2.不同路径Ⅱ3.下降路径最小和4.珠宝的最高价值5.地下城游戏 总结 二维DP模型 二维动态规划(DP)模型是一种通过引入两个维度的状态和转移方程来解决复杂问题的技术。它在许多优化和…...

Halcon OCR字符识别(极坐标转换,字符识别)
Halcon OCR字符识别(极坐标转换,字符识别) 代码 * 1.加载图片 *************************************************** dev_close_window () read_image (Image, ./img) get_image_size (Image, Width, Height) dev_get_window (WindowHandle…...

【管理咨询宝藏139】某大型快消集团公司多渠道销售管理体系方案
本报告首发于公号“管理咨询宝藏”,如需阅读完整版报告内容,请查阅公号“管理咨询宝藏”。 【管理咨询宝藏139】某大型快消集团公司多渠道销售管理体系方案 【格式】PDF版本 【关键词】罗兰贝格、营销咨询、战略规划 【核心观点】 - 销售体系建设主要需…...

大模型提问中包括时间的实战方案
大家好,我是herosunly。985院校硕士毕业,现担任算法研究员一职,热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名,CCF比赛第二名,科大讯飞比赛第三名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的见解。曾经辅导过若干个非计算机专业的学生进入到算法…...

【算法】(C语言):堆排序
堆(二叉树的应用): 完全二叉树。最大堆:每个节点比子树所有节点的数值都大,根节点是最大值。父子索引号关系(根节点为0):(向上)子节点x,父节点(x…...
ffmpeg下载/配置环境/测试
一、下载 1、访问FFmpeg官方网站下载页面:FFmpeg Download Page; 2、选择适合Windows的版本(将鼠标移动到windows端)。通常,你会找到“Windows builds from gyan.dev”或者“BtbN GitHub Releases”等选项࿰…...
C# 异步编程详解(Task,async/await)
文章目录 1.什么是异步2.Task 产生背景3.Thread(线程) 和 Task(异步)的区别3.1 几个名词3.2 Thread 与 Task 的区别 4.Task API4.1 创建和启动任务4.2 Task 等待、延续和组合4.3 task.Result4.4 Task.Delay() 和 Thread.Sleep() 区别 5.CancellationToken 和 CancellationToken…...
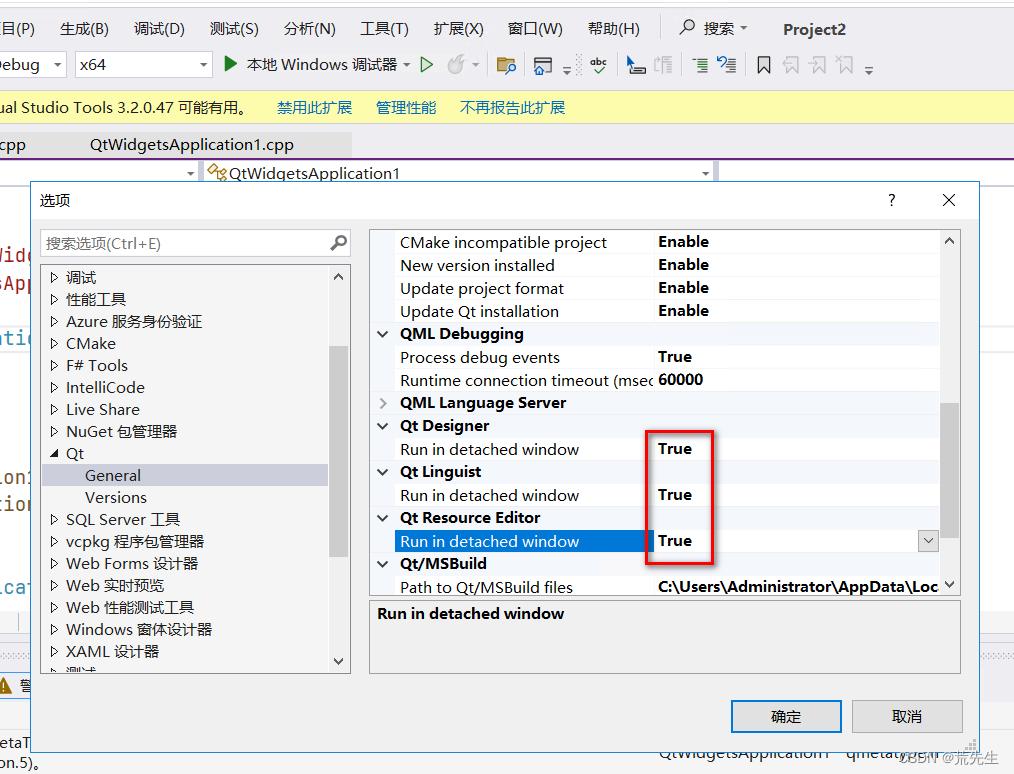
qt结合vs2022安装
进入清华大学开源软件: 清华大学开源软件镜像站 | Tsinghua Open Source Mirror 下载完成后,双击进行安装: 进入邮箱进行验证: 可能是因为网络问题,无法安装。 重新安装5.12.12版本。 安装后启动失败,重新…...

Kafka集群部署(手把手部署图文详细版)
1.1.1 部署zookpeer 在node02下载并解压zookeeper软件包 cd /usr/local wget https://archive.apache.org/dist/zookeeper/zookeeper-3.4.6/zookeeper-3.4.6.tar.gz 或者:scp cat192.168.28.100:/home/cat/zookeeper-3.4.6.tar.gz /tmp(注意目录…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
