DP:解决路径问题
文章目录
- 二维DP模型
- 如何解决路径问题
- 有关路径问题的几个问题
- 1.不同路径
- 2.不同路径Ⅱ
- 3.下降路径最小和
- 4.珠宝的最高价值
- 5.地下城游戏
- 总结

二维DP模型
二维动态规划(DP)模型是一种通过引入两个维度的状态和转移方程来解决复杂问题的技术。它在许多优化和组合问题中广泛应用,尤其是那些需要考虑二维数组或矩阵的情况。
以下是二维DP模型的核心概念和步骤:
-
状态定义:二维DP模型使用一个二维数组(或矩阵)来表示问题的状态。每个状态通常由两个变量(例如i和j)表示,表示在问题空间中的某个位置或状态。
-
状态转移方程:这是DP的核心。它描述了如何从一个状态转移到另一个状态,通常是通过递推关系来实现。转移方程基于问题的具体特性进行设计。
-
初始状态和边界条件:在DP表格中需要明确初始状态和边界条件。这些条件为DP表格的填充提供了起点。
-
目标状态:最后,我们通过目标状态来得到问题的最终解。通常是二维数组中的一个或几个特定位置。
如何解决路径问题
路径问题是动态规划中非常经典的一类问题,通常涉及从一个起点到一个终点的最短路径、最大路径或独特路径数等。解决路径问题的常用方法包括递归、回溯和动态规划(DP)。其中,动态规划由于其效率和易理解性,成为解决路径问题的常用技术。以下是解决路径问题的一些常见步骤和示例:
一般步骤
-
定义状态:确定DP数组的含义,通常是定义dp[i][j]表示从起点到位置(i, j)的某种路径属性(如路径和、路径数等)。
-
状态转移方程:建立递推关系,描述如何从一个状态转移到另一个状态。
-
初始化:根据问题的具体情况,设置DP数组的初始值。
-
计算DP数组:按照状态转移方程填充DP数组。
-
提取结果:通过DP数组得到最终结果。
有关路径问题的几个问题
1.不同路径
题目链接
题目:
样例输出和输入:
这道题是一个很典型的二维DP问题,也是二维DP中的路径问题的一种,这道题给定一个宽是m,长是n,让我们求在这个二位数组中从[0,0]点到[m-1,n-1]的方法有多少种。
算法原理:
算法原理也和传统的DP问题的步骤是一样的。
第一步:状态表示,先确定dp表是初始位置还是 末位置,很显然这道题要我们求的是方法有多少种,dp肯定是末位置,所以这里dp[i][j]到达[i,j]位置时有多少种方法。
第二步:状态转移方程,这道题dp表示的是到达某位置时的方法的种数,

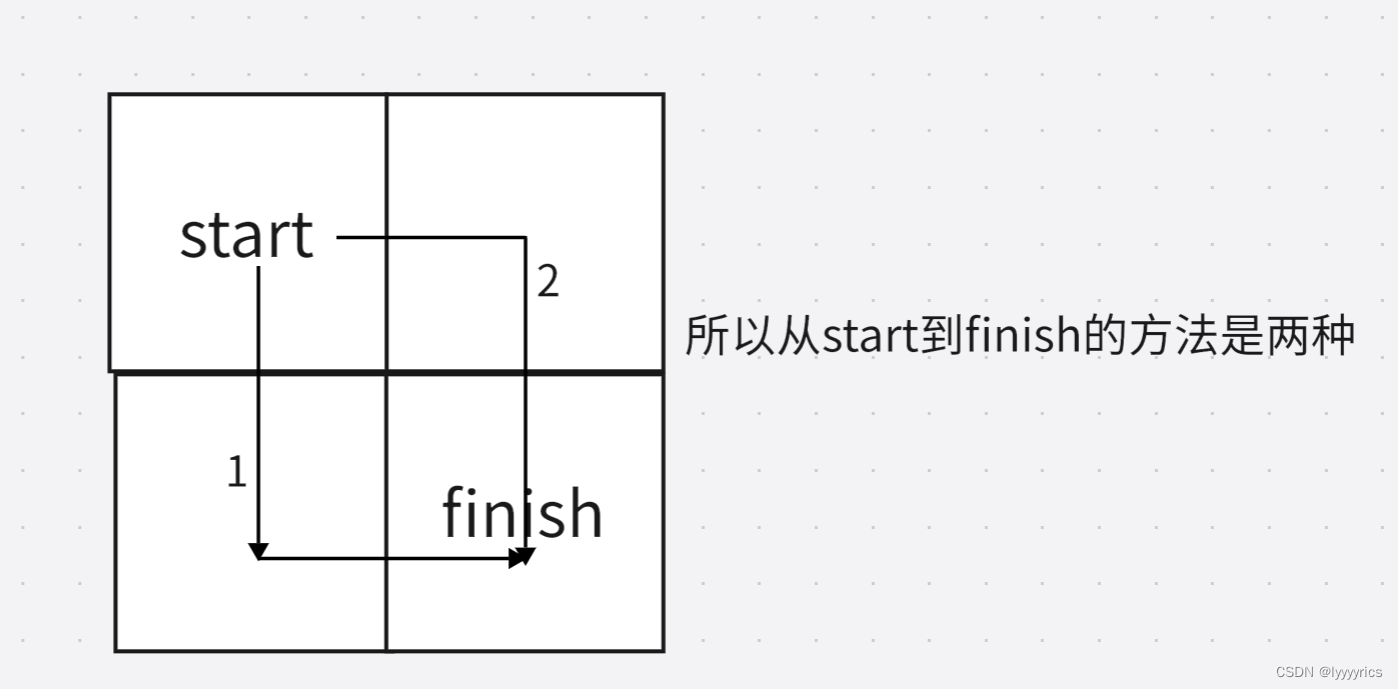
很显然这道题题目要求只能向下或者向右移动,所以我们只有可能从[i,j]位置的上方或者[i,j]的左方到达[i,j]位置,所以我们需要求[i,j]位置的最多的方法数,只需要求出左边和上面的方法总数之和即可。
状态转移方程:dp[i][j]=dp[i-1][j]+dp[i][j-1]
第三步:初始化问题,这道题的当前数据需要用到左边的数据和上面的数据,所以这道题越界的地方应该是红色的地方: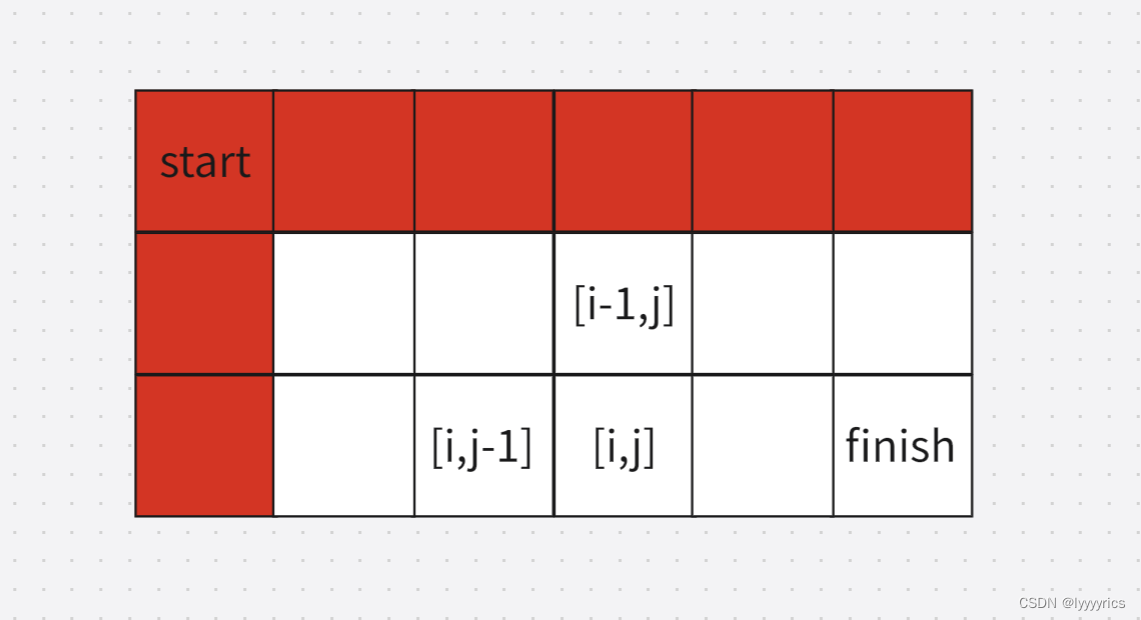
处理这种越界情况我们初始化只需要多开辟一行一列数组:
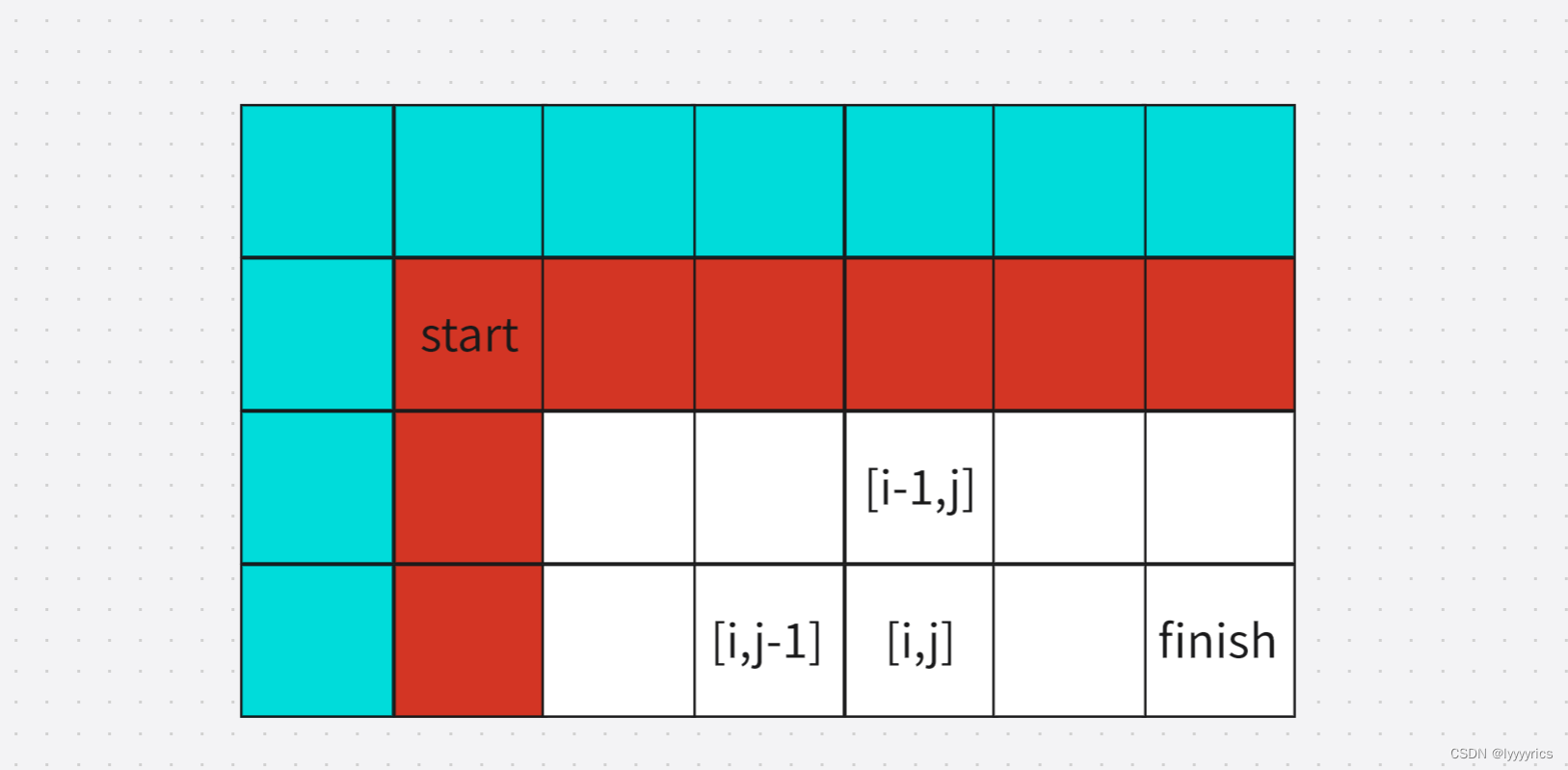
这样就不会出现越界的情况了,初始化应该把蓝色的部分全部初始化掉,具体初始哈为多少了,首先这相当于是一个虚拟的节点,为了防止越界而产生的,所以先初始化为0,但是如果初始化为零那么总的方法数就是零了,所以我们需要把[0,1]位置或者[1,0]位置初始化为1.
第四步:填表顺序,这道题很显然是从左上角开始 按顺序遍历。
第五步:返回值问题,这道题求的是到达左下角的方法总数,所以是返回dp[m][n]。
代码展示:
class Solution {
public:int uniquePaths(int m, int n) {//创建一个dp表,第一排和第一列表示虚拟节点vector<vector<int>> dp(m+1,vector<int>(n+1,0));//初始化[0,1]节点dp[0][1]=1;//填表for(int i=1;i<m+1;i++){for(int j=1;j<n+1;j++){//状态转移方程dp[i][j]=dp[i-1][j]+dp[i][j-1];}}//返回值return dp[m][n];}
};
运行结果:
2.不同路径Ⅱ
题目链接
题目:
样例输出和输入:
算法原理:
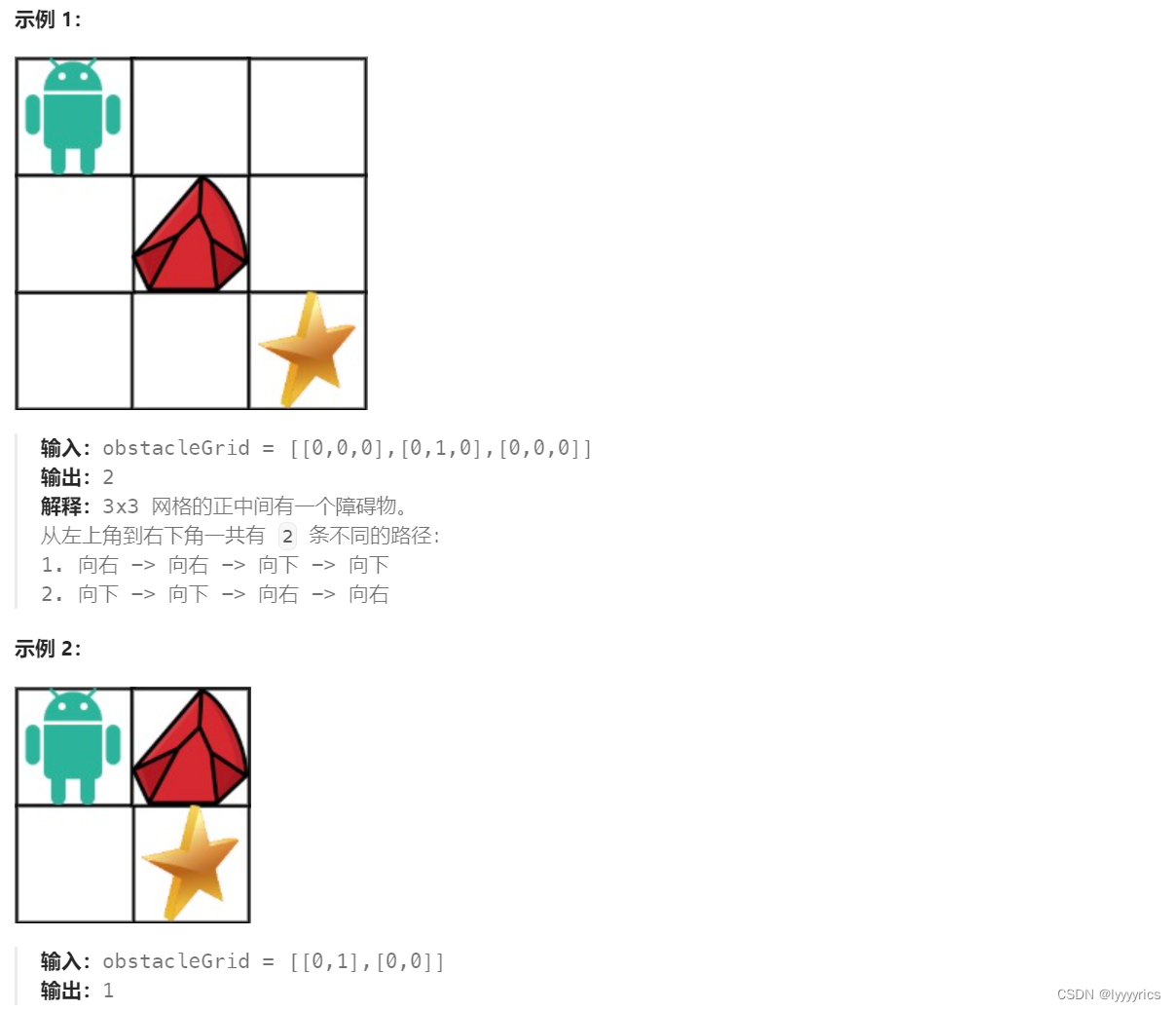
这道题和上一道题其实是一样的,只需要加一个判断,如果obstacleGrid数组中的值是1的话当前方法数就是0,所以在上道题的条件下加一个if条件的判断即可 。
代码展示:
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m=obstacleGrid.size();int n=obstacleGrid[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1,0));dp[0][1]=1;for(int i=1;i<m+1;i++){for(int j=1;j<n+1;j++){if(obstacleGrid[i-1][j-1]==0){dp[i][j]=dp[i-1][j]+dp[i][j-1];}}}return dp[m][n];}
};
运行结果:
3.下降路径最小和
题目链接
题目:
样例输出和输入:
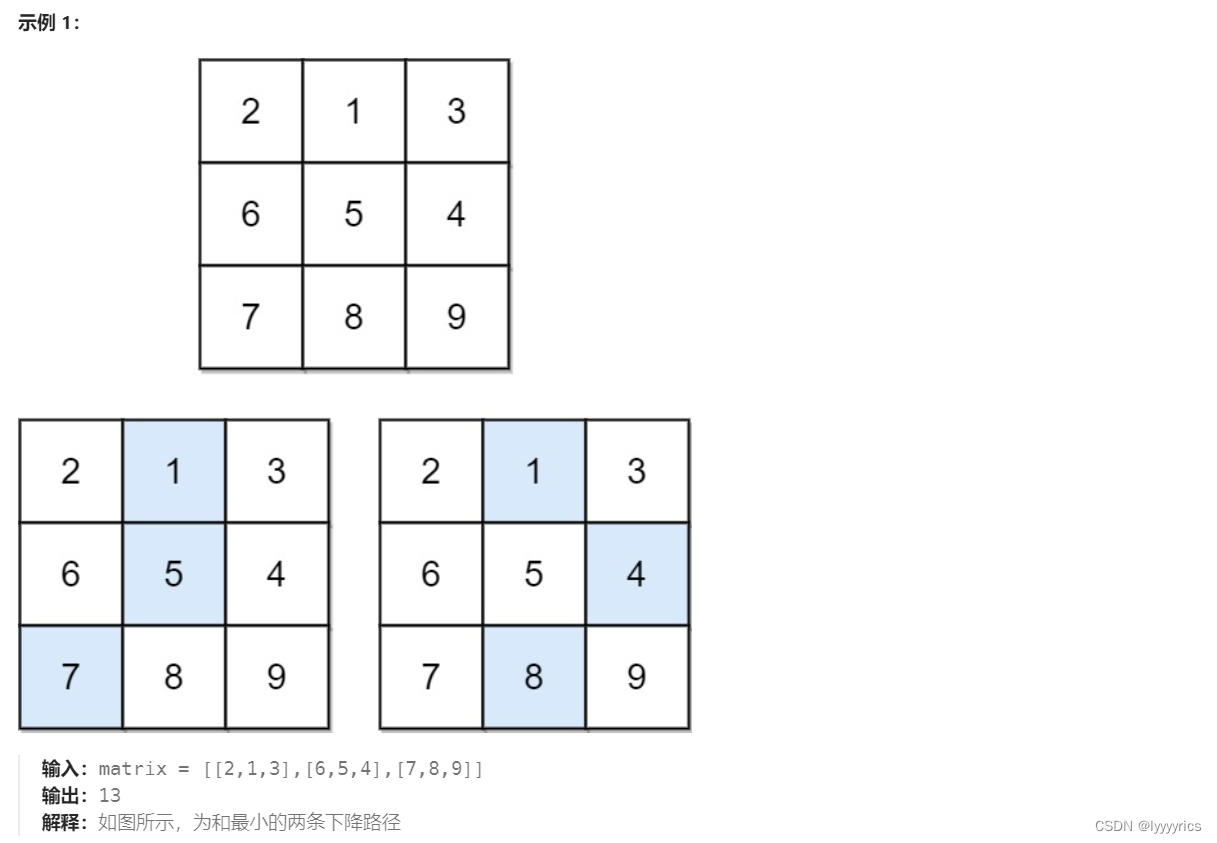
这道题的题意很简单,我们首先可以在一个n*n的矩阵的第一行 选三个数
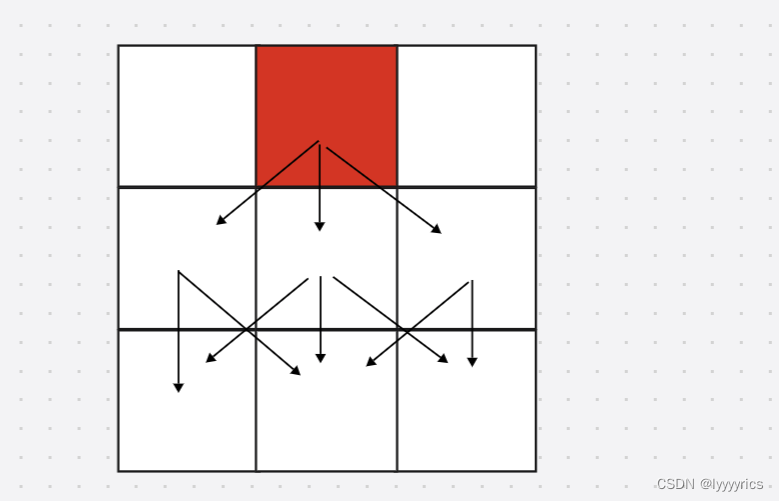
当我们选中间的格子时,可以下降的格子,我们假设当前格子的下标是[i,j],则可以访问的下一行的下降的格子应该是:[i+1,j-1] [i+1,j] [i+1,j+1]这三个下标,这道题让 我们求的就是到达最后一行的时候下降的最小的路径和,每个方格中的值就表示当前格子的路径数,所以当到达最后一行的时候走过的路径和就是走过的所有格子的值的和。
算法原理:
第一步:状态表示,这道题根据问题我们就知道这道题求的是下降路径最小和,所以我们的dp[i][j]表示的是到达[i][j]位置的时候的当前最小和。
第二步:状态转移方程,我们假设一个格子的下标是[i,j]。
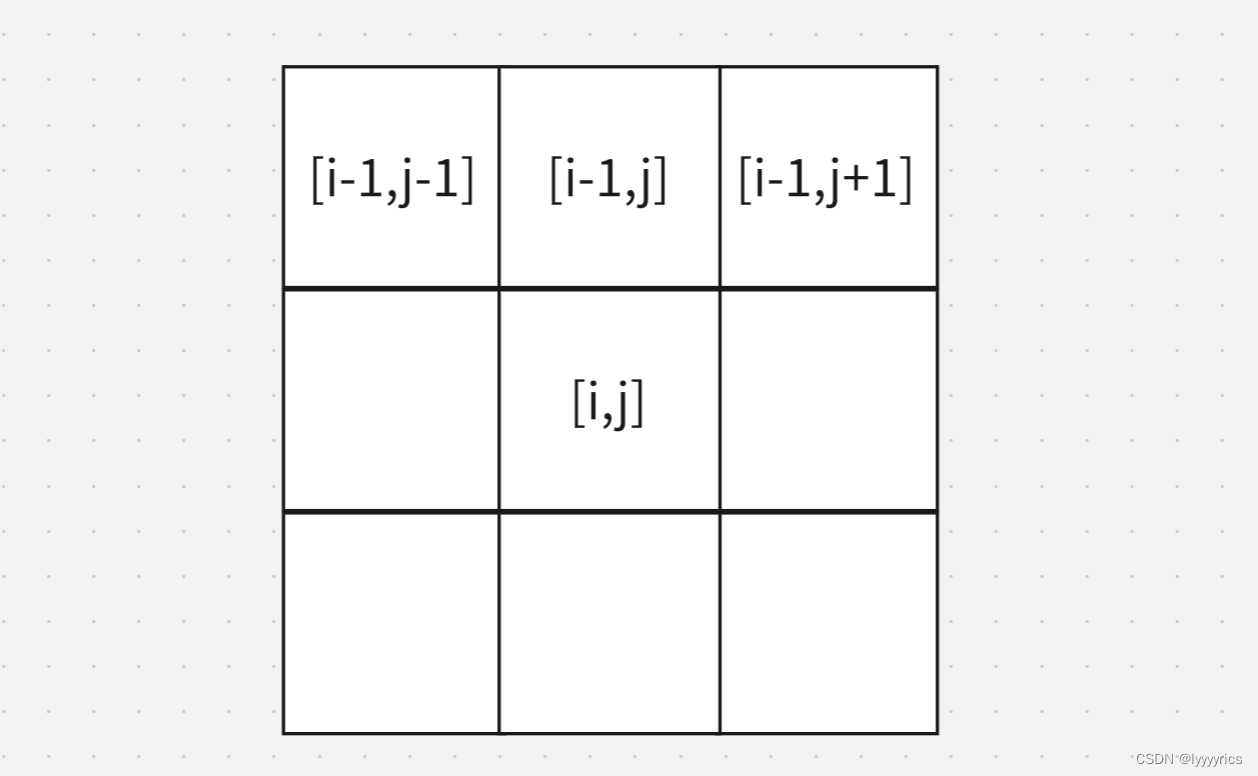
[i,j]的最小下降路径是不是应该等于上面三个的相邻的格子的最小路径加上当前格子的值。
所以状态转移方程应该是:dp[i][j]=min(dp[i-1][j],dp[i-1][j-1],dp[i-1][j+1])+matrix[i][j]
第三步:初始化为题,其实初始化还是和上面的一样,但是因为我们要用到上一行左边和右边的格子,所以这里会出现越界的格子不止左边和上面的格子还有右边的格子
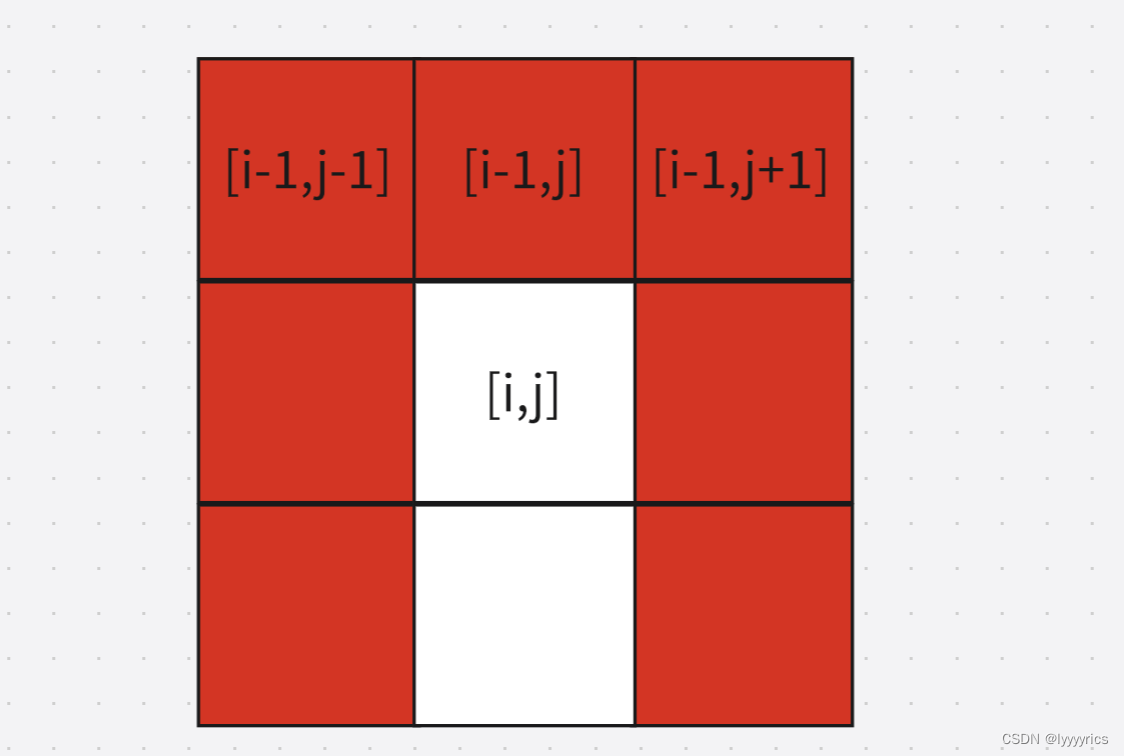
所以我们开辟空间应该这样开辟:
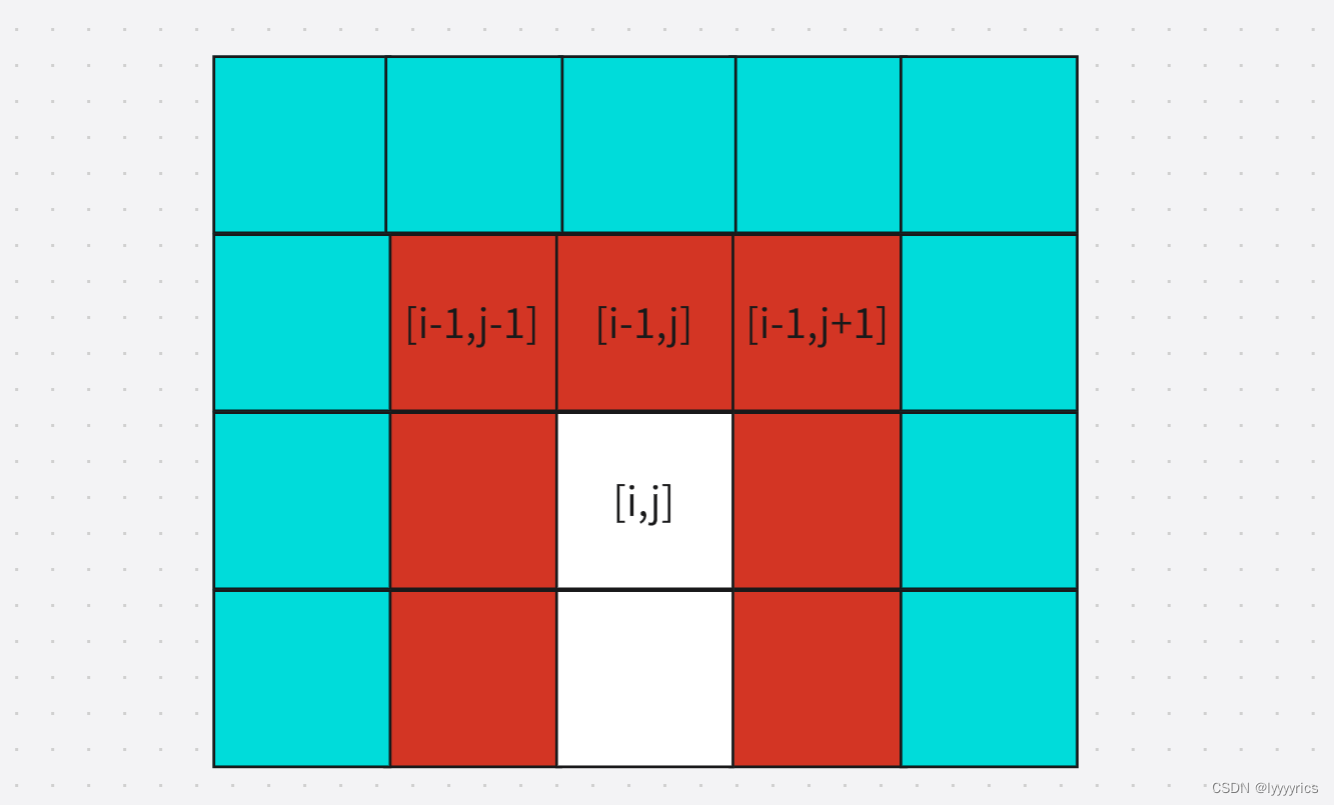
初始化应该初始化蓝色格子,由于当我们请求[i,j-1]位置的最小路径和的时候最左边的一列会影响最小值的大小,,所以这里初始化不能初始化为零,应该初始化为正无穷(INT_MAX)右边的蓝色格子也 应该初始化为正无穷,但是上面一排的格子应该初始化为0,这样才不会影响结果。
第四步:填表顺序,填表 顺序按顺序遍历。
第五步 :返回值,由于这道题求的是最小路径和,所以应该返回dp数组中最后一行中的最小值。
代码展示:
class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int m=matrix.size();int n=matrix[0].size();vector<vector<int>> dp(m+1,vector<int>(n+2,INT_MAX));for(int j=0;j<n+2;j++){dp[0][j]=0;}for(int i=1;i<m+1;i++){for(int j=1;j<n+1;j++){dp[i][j]=min(min(dp[i-1][j-1],dp[i-1][j]),dp[i-1][j+1])+matrix[i-1][j-1];}}int Min=INT_MAX;for(int j=0;j<n+2;j++){Min=min(Min,dp[m][j]);}return Min;}
};
运行结果:
4.珠宝的最高价值
题目链接
题目:
样例输出和输入:
这道题让我们求出珠宝的最高价值,
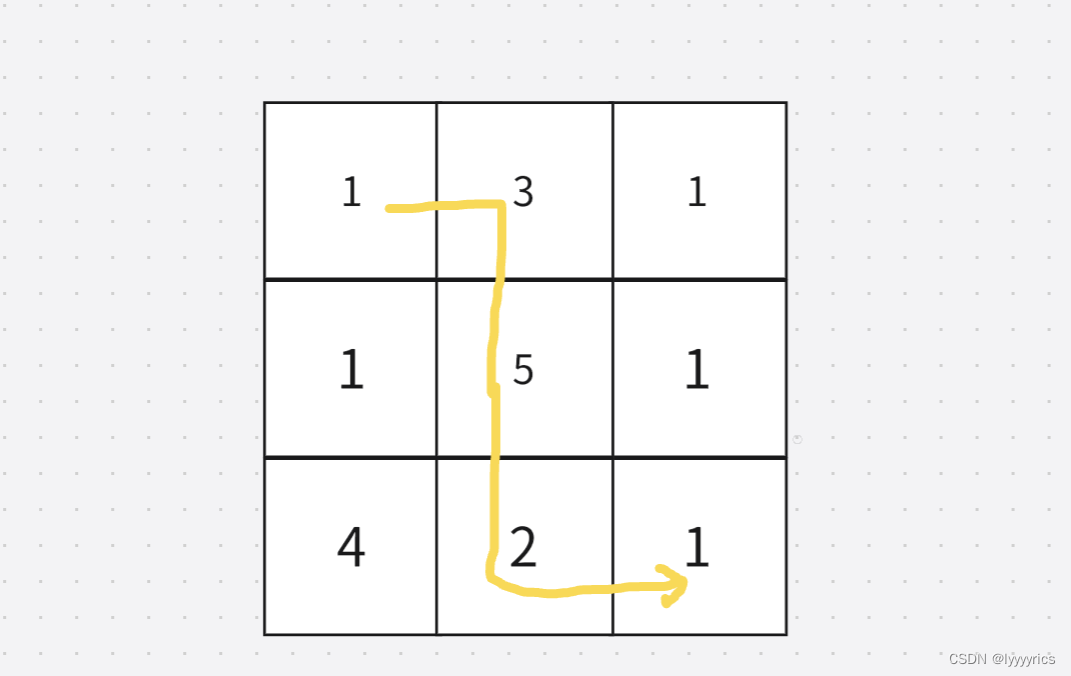
很显然根据示例一种的例子,价值最高的珠宝应该是这条路线之和,然后返回
算法原理:
状态表示:dp[i][j]当前位置的珠宝的最高价值。
状态转移方程:max(dp[i-1][j]+frame[i-1][j-1],dp[i][j-1]+frame[i-1][j-1])
初始化:初始化 应该初始化最左边和最上面,初始化为零,因为当前的礼物价值是0.
代码展示:
class Solution {
public:int jewelleryValue(vector<vector<int>>& frame) {int m=frame.size();int n=frame[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1,0));for(int i=1;i<m+1;i++){for(int j=1;j<n+1;j++){dp[i][j]=max(dp[i-1][j]+frame[i-1][j-1],dp[i][j-1]+frame[i-1][j-1]);}}return dp[m][n];}
};
运行结果:
5.地下城游戏
题目链接
题目:
样例输出和输入:
这道题让我们求出就出公主需要的最小健康值,当我们找到最小的一个路径的和加上1就是需要的最小的健康值。
算法原理:
状态表示:dp[i][j]表示当前位置救出公主需要的最小的健康程度,所以这道题的dp[i][j]应该是起点,而不是终点。
状态转移方程:我们设当前位置的最小的健康程度是dp[i][j],则当我们用dp[i][j]-dungeon[i][j]>=dp[i+1][j],同理还有一种情况:dp[i][j]-dungeon[i][j]>=dp[i][j+1]所以最小的健康程度应该是求一个最小值,则状态转移方程:dp[i][j]=min(dp[i+1][j],dp[i][j+1])-dungeon[i][j],但是需要注意的是如果dungeon是一个很大的正值的时候,会出现负数,由于这道题的题目要求是最低的健康值是1,到0或者小于零就死了,所以这道题不能出现负数,所以应该和1取一下max。
初始化,初始化我们和以前不一样,应该:
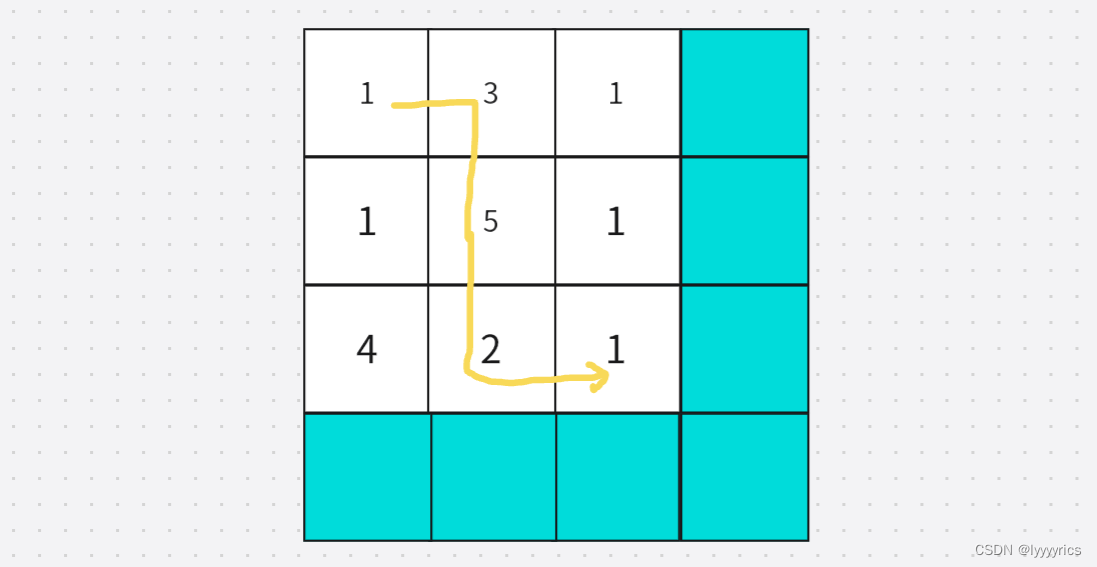
应该初始化左下角,由于取的最小值,所以不能初始化为0,应该初始化为INT_MAX,但是公主下面的和右边的格子应该初始化为1,因为救完公主的最小健康值是1,所以应该初始化为1.
填表顺序:从右下角倒着填表
返回值:返回dp数组的第一个值。
代码展示:
class Solution {
public:int calculateMinimumHP(vector<vector<int>>& dungeon) {int m=dungeon.size();int n=dungeon[0].size();vector<vector<int>> dp(m+1,vector<int>(n+1,INT_MAX));dp[m][n-1]=1;dp[m-1][n]=1;for(int i=m-1;i>=0;i--){for(int j=n-1;j>=0;j--){dp[i][j]=min(dp[i+1][j],dp[i][j+1])-dungeon[i][j];dp[i][j]=max(dp[i][j],1);}}return dp[0][0];}
};
运行结果:
总结
在这篇博客中,我们详细探讨了动态规划(DP)在解决路径问题中的应用。我们首先回顾了动态规划的基本概念和其核心思想,即通过将问题分解为更小的子问题并存储其结果来避免重复计算。然后,我们通过多个经典的路径问题示例,如最短路径问题、最长路径问题和独特路径问题,展示了如何将动态规划技术应用于实际问题中。
通过这些示例,我们可以看到,动态规划不仅提高了算法的效率,还提供了一种系统化的思维方式,使我们能够更加清晰地理解和解决复杂的路径问题。掌握动态规划技巧,不仅有助于我们在学术研究中取得突破,还能在实际工程项目中大幅度提高解决问题的能力。
希望通过这篇博客,读者们能够更好地理解动态规划的基本原理和应用场景,并在未来的学习和工作中灵活运用这一强大的工具。感谢阅读,如果您有任何问题或建议,欢迎在评论区与我交流。
相关文章:

DP:解决路径问题
文章目录 二维DP模型如何解决路径问题有关路径问题的几个问题1.不同路径2.不同路径Ⅱ3.下降路径最小和4.珠宝的最高价值5.地下城游戏 总结 二维DP模型 二维动态规划(DP)模型是一种通过引入两个维度的状态和转移方程来解决复杂问题的技术。它在许多优化和…...

Halcon OCR字符识别(极坐标转换,字符识别)
Halcon OCR字符识别(极坐标转换,字符识别) 代码 * 1.加载图片 *************************************************** dev_close_window () read_image (Image, ./img) get_image_size (Image, Width, Height) dev_get_window (WindowHandle…...

【管理咨询宝藏139】某大型快消集团公司多渠道销售管理体系方案
本报告首发于公号“管理咨询宝藏”,如需阅读完整版报告内容,请查阅公号“管理咨询宝藏”。 【管理咨询宝藏139】某大型快消集团公司多渠道销售管理体系方案 【格式】PDF版本 【关键词】罗兰贝格、营销咨询、战略规划 【核心观点】 - 销售体系建设主要需…...

大模型提问中包括时间的实战方案
大家好,我是herosunly。985院校硕士毕业,现担任算法研究员一职,热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名,CCF比赛第二名,科大讯飞比赛第三名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的见解。曾经辅导过若干个非计算机专业的学生进入到算法…...

【算法】(C语言):堆排序
堆(二叉树的应用): 完全二叉树。最大堆:每个节点比子树所有节点的数值都大,根节点是最大值。父子索引号关系(根节点为0):(向上)子节点x,父节点(x…...
ffmpeg下载/配置环境/测试
一、下载 1、访问FFmpeg官方网站下载页面:FFmpeg Download Page; 2、选择适合Windows的版本(将鼠标移动到windows端)。通常,你会找到“Windows builds from gyan.dev”或者“BtbN GitHub Releases”等选项࿰…...
C# 异步编程详解(Task,async/await)
文章目录 1.什么是异步2.Task 产生背景3.Thread(线程) 和 Task(异步)的区别3.1 几个名词3.2 Thread 与 Task 的区别 4.Task API4.1 创建和启动任务4.2 Task 等待、延续和组合4.3 task.Result4.4 Task.Delay() 和 Thread.Sleep() 区别 5.CancellationToken 和 CancellationToken…...
qt结合vs2022安装
进入清华大学开源软件: 清华大学开源软件镜像站 | Tsinghua Open Source Mirror 下载完成后,双击进行安装: 进入邮箱进行验证: 可能是因为网络问题,无法安装。 重新安装5.12.12版本。 安装后启动失败,重新…...

Kafka集群部署(手把手部署图文详细版)
1.1.1 部署zookpeer 在node02下载并解压zookeeper软件包 cd /usr/local wget https://archive.apache.org/dist/zookeeper/zookeeper-3.4.6/zookeeper-3.4.6.tar.gz 或者:scp cat192.168.28.100:/home/cat/zookeeper-3.4.6.tar.gz /tmp(注意目录…...

阿里Qwen2-72B大模型已是开源榜的王者,为什么还要推出其他参数模型,被其他模型打榜?
6 月 27 日,全球知名的开源平台 Hugging Face 的联合创始人兼首席执行官 Clem 在社交平台激动宣布,阿里 Qwen2-72B 成为了开源模型排行榜的王者。 这是一件大好事,说明了我们在大模型领域从先前的追赶,逐渐走向了领导,…...
7.基于SpringBoot的SSMP整合案例-表现层开发
目录 1.基于Restfu1进行表现层接口开发 1.1创建功能类 1.2基于Restful制作表现层接口 2.接收参数 2使用Apifox测试表现层接口功能 保存接口: 分页接口: 3.表现层一致性处理 3.1先创建一个工具类,用作后端返回格式统一类:…...

【server】3、注册中心与配置中心
1、服务注册与发现 1.1、consul 1.1.1 是什么 官网: Consul by HashiCorp spring-cloud-consul: Spring Cloud Consul :: Spring Cloud Consul gitHub 官网 :GitHub - hashicorp/consul: Consul is a distributed, highly available, and data cent…...

【大数据】—量化交易实战案例(海龟交易策略)
声明:股市有风险,投资需谨慎!本人没有系统学过金融知识,对股票有敬畏之心没有踏入其大门,今天用另外一种方法模拟炒股,后面的模拟的实战全部用同样的数据,最后比较哪种方法赚的钱多。 海龟交易…...

014-GeoGebra基础篇-快速解决滑动条的角度无法输入问题
有客户反馈,他的Geogebra一直有个bug,那就是输入角度最大值时总不按照他设定的展示,快被气炸了~ 目录 一、问题复现(1)插入一个滑动条(2)选择Angle(3)输入90,…...
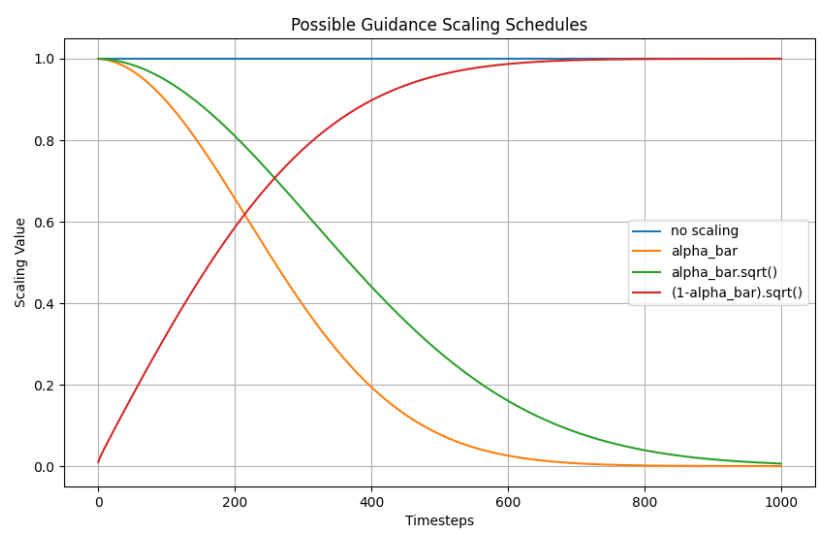
Diffusion模型的微调和引导
留意后续更新,欢迎关注微信公众号:组学之心 Diffusion模型的微调和引导 微调(fine-tuning): 从一个已经训练过的模型开始训练,我们就可以从一个学会如何“去噪”的模型开始训练,相对于随机初始…...

零基础学MySQL:从入门到实践的完整指南
引言: MySQL,作为全球最受欢迎的开源关系型数据库管理系统之一,以其高性能、易用性和灵活性,在Web开发、数据分析等领域占据着举足轻重的地位。如果你是一位编程新手,想要踏入数据库管理的大门,本文将从零…...

澳蓝荣耀时刻,6款产品入选2024年第一批《福州市名优产品目录》
近日,福州市工业和信息化局公布2024年第一批《福州市名优产品目录》,澳蓝自主研发生产的直接蒸发冷却空调、直接蒸发冷却组合式空调机组、间接蒸发冷水机组、高效间接蒸发冷却空调机、热泵式热回收型溶液调湿新风机组、防火湿帘6款产品成功入选。 以上新…...

Frrouting快速入门——OSPF组网(一)
FRR简介 FRR是FRRouting的简称,是一个开源的路由交换软件套件。其作者源自老牌项目quaga的成员,也可以算是quaga的新版本。 使用时一般查看此文档:https://docs.frrouting.org/projects/dev-guide/en/latest/index.html FRR支持的协议众多…...

记录通过Cloudflare部署属于自己的docker镜像源
引言 由于最近国内无法正常拉取docker镜像,然而找了几个能用的docker镜像源发现拉取回来的docker镜像不是最新的版本,部署到Cloudflare里Workers 和 Pages,拉取docker 镜像成功,故记录部署过程。 部署服务 登录Cloudflare后&…...

波动方程 - 在三维图中动态显示二维波动方程的解就像水面波澜起伏
波动方程 - 在三维图中动态显示二维波动方程的解就像水面波澜起伏 flyfish 波动方程的求解结果通常不是一个单一的数值,而是一个函数或一组函数,这些函数描述了波随时间和空间的传播情况。具体来说,波动方程的解可以是关于时间和空间变量的…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...