简单的自定义录屏工具
在csdn上写文章,需要配一些操作动态图,需要针对电脑录屏,可能是整个屏幕录屏,也可能是某窗口,甚至是某一小块区域。
动态图最好是gif格式,方便直接嵌入文章中。
一、设计
窗口类widget

切屏类Capturescreen
录屏类RecordScreen
线程类MyThread
【选择区域】:调用Capturescreen完成对屏幕自定义选择,回车键确认,ESC退出截屏
void Capturescreen::keyPressEvent(QKeyEvent *event)
{// Esc 键退出截图;if (event->key() == Qt::Key_Escape){close();}// Eeter键完成截图;if (event->key() == Qt::Key_Return || event->key() == Qt::Key_Enter){emit signalCompleteCature(m_capturePixmap);emit signalCompleteCatureInfo(selectedRect);close();m_beginPoint = m_endPoint = QPoint(0,0);}
}
【开始录制】:最多录制<1小时(37.5分钟),每秒40帧
【结束录制】:把每一帧保存成img下图片,并调用ffmpeg.exe合成test.mp4

【本地文件夹】:方便打开mp4所在文件夹
【mp4Togif】: 调用ffmpeg.exe把mp4转成gif格式,通过参数配置,保证不失真
二、演示
操作演示录屏

录屏效果

程序下载
https://download.csdn.net/download/chen_227/87570258
不需要积分
相关文章:

简单的自定义录屏工具
在csdn上写文章,需要配一些操作动态图,需要针对电脑录屏,可能是整个屏幕录屏,也可能是某窗口,甚至是某一小块区域。 动态图最好是gif格式,方便直接嵌入文章中。 一、设计 窗口类widget 切屏类Capturescr…...

数据结构与算法基础(王卓)(17):KMP算法详解(精讲(最简单、直接、有效的思路方法,答案以及代码原理)
本文具体思路参考: (最后证明,该教材/网课实际上是最有效的) DS第四章【3】KMP1_哔哩哔哩_bilibili 中间走的一些弯路的教材: 第06周05--第4章串、数组和广义表5-4.3串的操作--串的匹配算法2--KMP算法_哔哩哔哩_bi…...
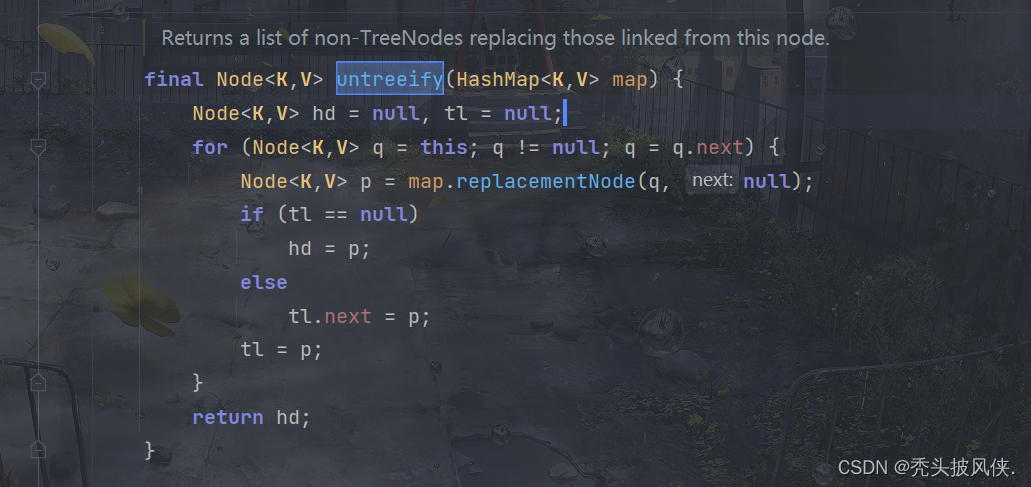
【java基础】HashMap源码解析
文章目录基础说明构造器put方法(无扩容,无冲突)put方法(无冲突,有扩容)put方法(有冲突,无树化)put方法(有冲突,树化)remove方法&#…...

实现异步的8种方式,你知道几个?
一、前言 在编程中,有时候我们需要处理一些费时的操作,比如网络请求、文件读写、数据库操作等等,这些操作会阻塞线程,等待结果返回。为了避免阻塞线程、提高程序的并发处理能力,我们常常采用异步编程。 异步编程是一种…...
二叉树的三种遍历
二叉树的遍历可以有:先序遍历、中序遍历、后序遍历先序遍历:根、左子树,右子树中序遍历:左子树、根、右子树后序遍历:左子树、右子树、根下面是我画图理解三种遍历:二叉树里都是分为左子树和右子树。分治思…...

我,30岁程序员被裁了,千万别干全栈
大家好,这里是程序员晚枫,今天是读者投稿。下面开始我们的正文。👇 关注博主👉程序员晚枫 很久了,今天给大家分享一下我从事程序员后,30岁被裁的经历,希望帮到有需要的人。 1、我被裁了 大家好…...
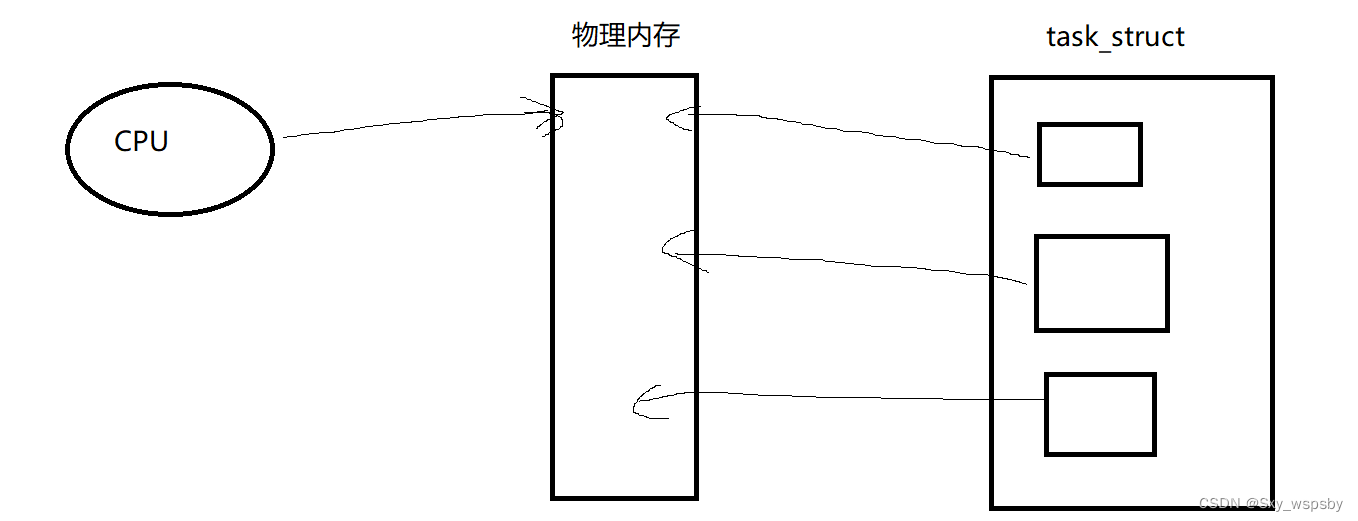
【linux】:进程地址空间
文章目录 前言一、进程地址空间总结前言 本篇文章接着上一篇文章继续讲解进程,主要讲述了进程在运行过程中是如何在内存中被读取的以及为什么要有虚拟地址的存在,CPU在运行过程中是拿到程序的虚拟地址还是真实的物理内存。 一、进程地址空间 下面我们先…...
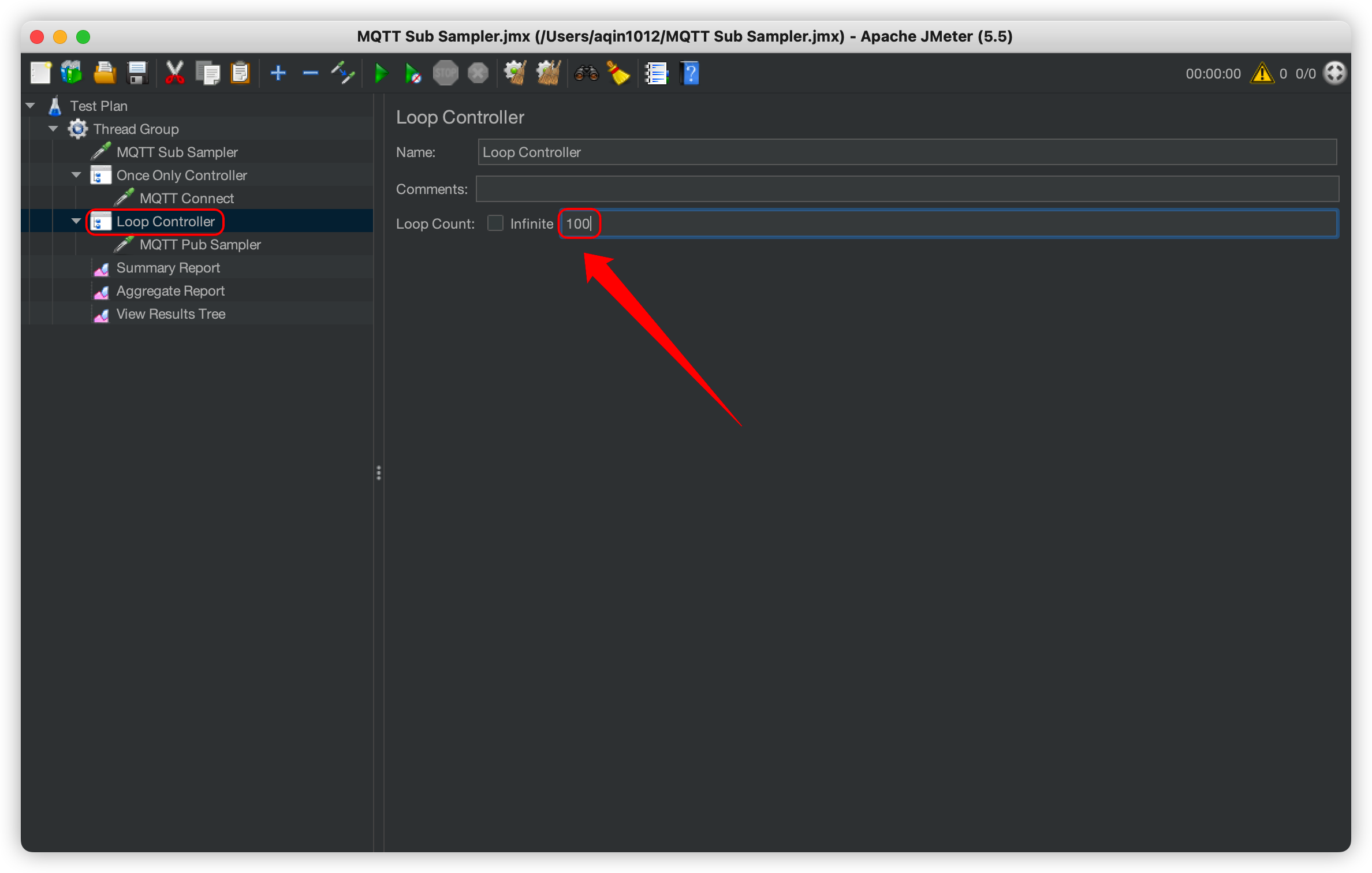
【保姆级】JMeter Mqtt 压测配置
忽然有个紧急任务要对某个服务做MQTT做压测,紧急实操下JMeter,这里记录下非专业测试员的测试过程、(▽`),欢迎👏大家检查指点( ̄∇ ̄)/下载⏬工具JMeter官方下载地址https://jmeter.apache.org/do…...

C语言数据结构初阶(4)----带头双向循环链表
我们先来看看带头双向循环链表的结构:看到这里我们可能会产生一个想法:这个链表看起来好复杂的样子,是不是它的增删改查比单链表更难写呢?嘿嘿,还真的不是这样的,双向链表的增删改查是很好写的哦࿰…...

原生javascript手写一个丝滑的轮播图
通过本文,你将学到: htmlcssjs 没错,就是html,css,js,现在是框架盛行的时代,所以很少会有人在意原生三件套,通过本文实现一个丝滑的轮播图,带你重温html,css和js基础知识。 为什么选用轮播图做示例&…...
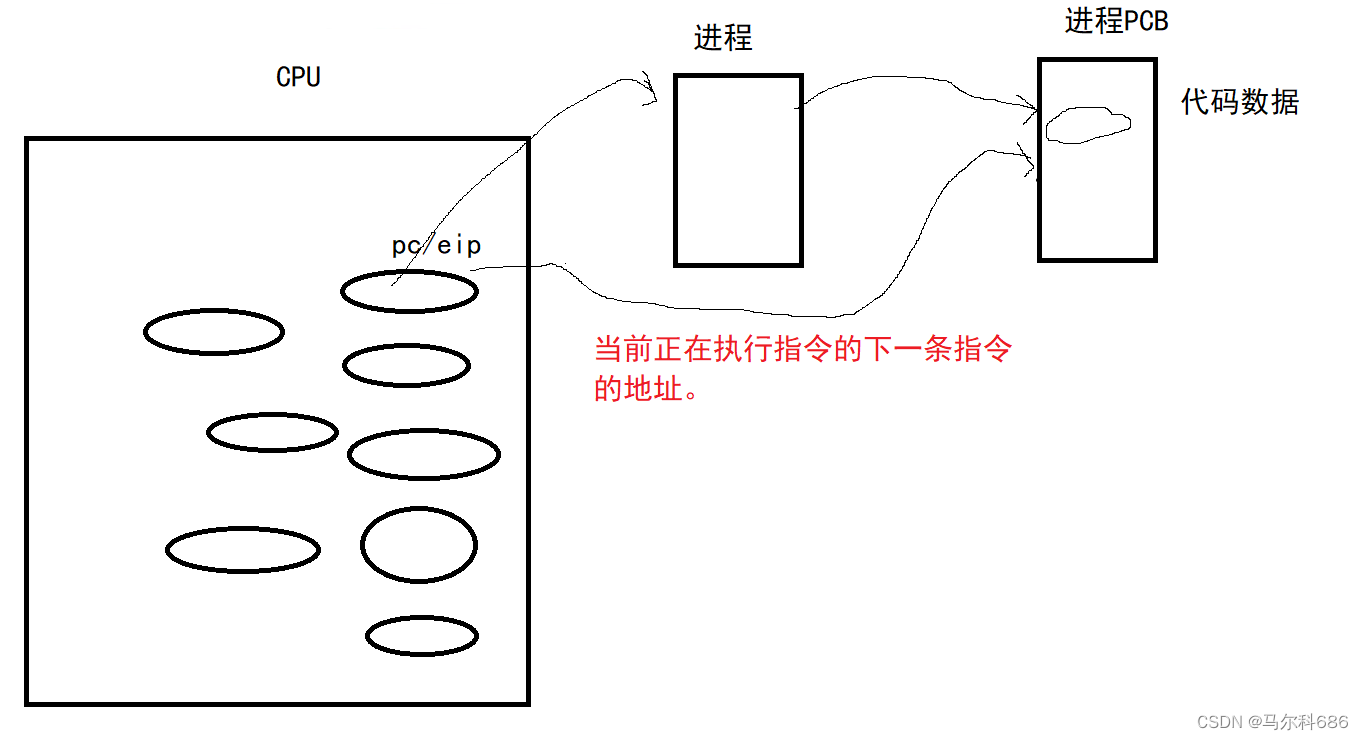
【Linux】进程优先级(进程优先级 Linux下优先级 用top命令更改已存在进程的nice 其他概念 进程切换)
文章目录进程优先级Linux下优先级用top命令更改已存在进程的nice:其他概念进程切换进程优先级 我们作为使用者一般不关心优先级,它跟我们的调度器有很大的关系,调度器是为了跟均衡的调度进程。 什么叫做优先级? 优先级和权限是两…...
2016年chatGPT之父Altman与马斯克的深度对话(值得一看)
2016年9月,现今OpenAI CEO,ChatGPT之父,时任创投公司Y Combinator的总裁Sam Altman在特斯拉加州弗里蒙特工厂采访了埃隆马斯克。马斯克阐述了创建OpenAI的初衷,以及就他而言,对于未来最为重要的五件事。这是OpenAI的两…...

基于vscode开发vue3项目的详细步骤教程 3 前端路由vue-router
1、Vue下载安装步骤的详细教程(亲测有效) 1_水w的博客-CSDN博客 2、Vue下载安装步骤的详细教程(亲测有效) 2 安装与创建默认项目_水w的博客-CSDN博客 3、基于vscode开发vue项目的详细步骤教程_水w的博客-CSDN博客 4、基于vscode开发vue项目的详细步骤教程 2 第三方图标库FontAw…...

【C语言】每日刷题 —— 牛客语法篇(5)
前言 大家好,继续更新专栏 c_牛客,不出意外的话每天更新十道题,难度也是从易到难,自己复习的同时也希望能帮助到大家,题目答案会根据我所学到的知识提供最优解。 🏡个人主页:悲伤的猪大肠9的博…...
操作系统(2.1)--进程的描述与控制
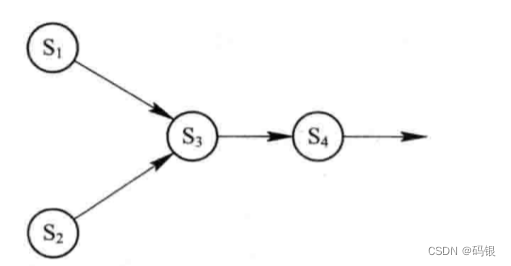
目录 一、前驱图和程序执行 1.前驱图 2.程序顺序执行 2.1 程序的顺序执行 2.2 程序顺序执行时的特征 3. 程序并发执行 3.1程序的并发执行 3.2 程序并发执行时的特征 一、前驱图和程序执行 1.前驱图 前趋图:是一个有向无循环图,用于描述进程之间执行的前后…...

JAVA查看动态代理类
JAVA查看代理类 1. 代理类 class 生成 System.setProperty // jdk8及之前的设置System.setProperty("sun.misc.ProxyGenerator.saveGeneratedFiles", "true");// or System.getProperties().put("sun.misc.ProxyGenerator.saveGenerated…...

Chapter2 : SpringBoot配置
尚硅谷SpringBoot顶尖教程 1. 全局配置文件 SpringBoot使用一个全局的配置文件 application.properties 或者 application.yml ,该配置文件放在src/main/resources目录或者类路径/config目录下面, 可以用来修改SpringBoot自动配置的默认值。 yml是YA…...

手撕单链表练习
Topic 1:LeetCode——203. 移除链表元素203. 移除链表元素 - 力扣(LeetCode)移除链表中的数字6操作很简单,我们只需要把2的指向地址修改就好了,原来的指向地址是6现在改为3这个思路是完全正确的,但是在链表…...

Kubuntu安装教程
文章目录Kubuntu介绍下载Kubuntu在VMware虚拟机中安装Kubuntu1. 点击“创建新的虚拟机”2. 选择“自定义(高级)”3. 按照下图所示进行设置设置网络4. 点击“自定义硬件”5. 开启虚拟机6. 进入安装界面,选择中文,之后点击“安装Kub…...
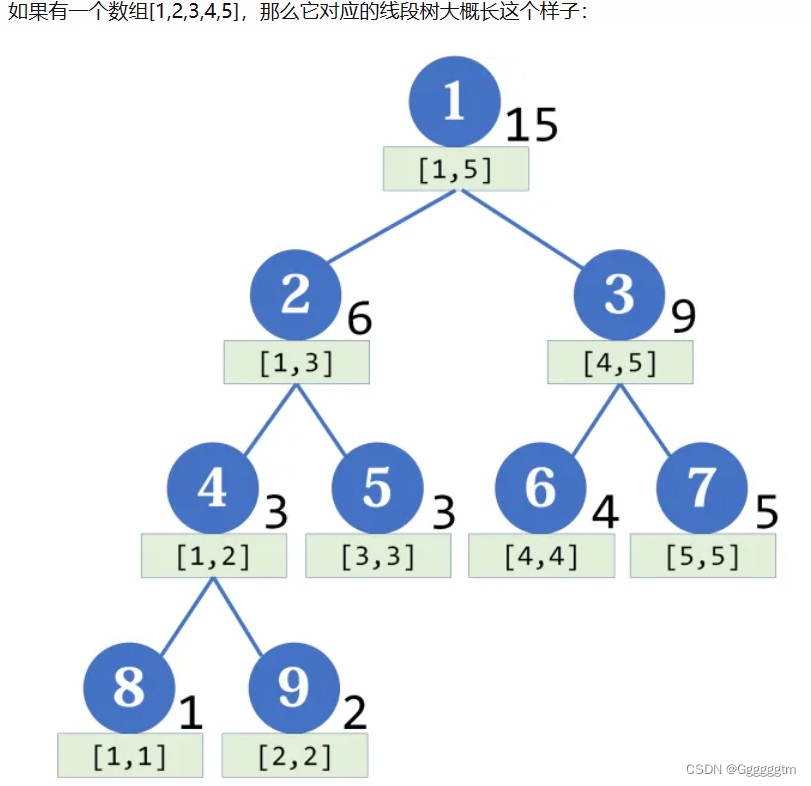
[蓝桥杯] 树状数组与线段树问题(C/C++)
文章目录 一、动态求连续区间和 1、1 题目描述 1、2 题解关键思路与解答 二、数星星 2、1 题目描述 2、2 题解关键思路与解答 三、数列区间最大值 3、1 题目描述 3、2 题解关键思路与解答 标题:树状数组与线段树问题 作者:Ggggggtm 寄语:与其…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...
