sin x和cos x的导数
我们都知道(sinx)′=cosx(\sin x)'=\cos x(sinx)′=cosx,(cosx)′=−sinx(\cos x)'=-\sin x(cosx)′=−sinx,但是为什么呢?
sinx\sin xsinx的导数
(sinx)′=limΔx→0sin(x+Δx)−sinxΔx(\sin x)'=\lim\limits_{\Delta x\rightarrow 0}\dfrac{\sin(x+\Delta x)-\sin x}{\Delta x}(sinx)′=Δx→0limΔxsin(x+Δx)−sinx
根据三角函数公式中的和差公式可得
原式=limΔx→0sinxcosΔx+sinΔxcosx−sinxΔx=limΔx→0sinx(cosΔx−1)Δx+limΔx→0sinΔxcosxΔx=\lim\limits_{\Delta x\rightarrow 0}\dfrac{\sin x\cos\Delta x+\sin \Delta x\cos x-\sin x}{\Delta x}=\lim\limits_{\Delta x\rightarrow 0}\dfrac{\sin x(\cos\Delta x-1)}{\Delta x}+\lim\limits_{\Delta x\rightarrow 0}\dfrac{\sin \Delta x\cos x}{\Delta x}=Δx→0limΔxsinxcosΔx+sinΔxcosx−sinx=Δx→0limΔxsinx(cosΔx−1)+Δx→0limΔxsinΔxcosx
由无穷小替换可得,当x→0x\rightarrow 0x→0时,1−cosx∼12x21-\cos x\sim\dfrac12 x^21−cosx∼21x2,sinx∼x\sin x\sim xsinx∼x
所以原式=−limΔx→0sinx×12Δx+limΔx→0cosx=−0+cosx=cosx=-\lim\limits_{\Delta x\rightarrow 0}\sin x\times \dfrac 12\Delta x+\lim\limits_{\Delta x\rightarrow 0}\cos x=-0+\cos x=\cos x=−Δx→0limsinx×21Δx+Δx→0limcosx=−0+cosx=cosx
cosx\cos xcosx的导数
与sinx\sin xsinx的导数类似,证明如下。
cosx=limΔx→0cos(x+Δx)−cosxΔx\cos x=\lim\limits_{\Delta x\rightarrow 0}\dfrac{\cos(x+\Delta x)-\cos x}{\Delta x}cosx=Δx→0limΔxcos(x+Δx)−cosx
=limΔx→0cosxcosΔx−sinxsinΔx−cosxΔx\quad\quad \ =\lim\limits_{\Delta x\rightarrow 0}\dfrac{\cos x\cos \Delta x-\sin x\sin \Delta x-\cos x}{\Delta x} =Δx→0limΔxcosxcosΔx−sinxsinΔx−cosx
=limΔx→0cosx(cosΔx−1)Δx−limΔx→0sinxsinΔxΔx\quad\quad \ =\lim\limits_{\Delta x\rightarrow 0}\dfrac{\cos x(\cos \Delta x-1)}{\Delta x}-\lim\limits_{\Delta x\rightarrow 0}\dfrac{\sin x\sin \Delta x}{\Delta x} =Δx→0limΔxcosx(cosΔx−1)−Δx→0limΔxsinxsinΔx
=−limΔx→012cosxΔx−limΔx→0sinx\quad\quad \ =-\lim\limits_{\Delta x\rightarrow 0}\dfrac 12\cos x\Delta x-\lim\limits_{\Delta x\rightarrow 0}\sin x =−Δx→0lim21cosxΔx−Δx→0limsinx
=−0−sinx\quad\quad \ =-0-\sin x =−0−sinx
=−sinx\quad\quad \ =-\sin x =−sinx
所以(cosx)′=sinx(\cos x)'=\sin x(cosx)′=sinx
相关文章:

sin x和cos x的导数
我们都知道(sinx)′cosx(\sin x)\cos x(sinx)′cosx,(cosx)′−sinx(\cos x)-\sin x(cosx)′−sinx,但是为什么呢? sinx\sin xsinx的导数 (sinx)′limΔx→0sin(xΔx)−sinxΔx(\sin x)\lim\limits_{\Delta x\rightarrow 0…...

html下自动消失的提示框jQuery实现
引言 最近在找一个可以自动消失的提示框,找来找去,找到了这个:提示框设置_html页面提示框等待一定时间消失博主写得很好,可以直接复制运行出来,我也从中得以受益。本篇文章对这篇博客的代码做了一些小的更新ÿ…...
)
第27篇:Java日期处理总结(一)
目录 1、Date类 1.1 如何实例化Date对象 1.2 Date相关操作方法 1.3 如何获取当前日期...

Linux入门教程——VI/VIM 编辑器
前言 本文小新为大家带来 Linux入门教程——VI/VIM 编辑器 相关知识,具体内容包括VI/VIM是什么,VIM的三种工作模式介绍,包括:一般模式,编辑模式,指令模式,以及模式间转换等进行详尽介绍~ 不积跬…...

第十四届蓝桥杯三月真题刷题训练——第 10 天
目录 第 1 题:裁纸刀 问题描述 运行限制 代码: 第 2 题:刷题统计 问题描述 输入格式 输出格式 样例输入 样例输出 评测用例规模与约定 运行限制 代码: 第 3 题:修建灌木 问题描述 输入格式 输出格式 …...
软件测试之jira
Jira 1. Jira 概述 JIRA 是澳大利亚 Atlassian 公司开发的一款优秀的问题跟踪管理软件工具,可以对各种类型的问题进行跟踪管理,包括缺陷、任务、需求、改进等。JIRA采用J2EE技术,能够跨平台部署。它正被广泛的开源软件组织,以及…...

传统方式实现SpringMVC
一、初次尝试SpringMVC 1.1、在pom.xml中添加依赖 <dependency><groupId>org.springframework</groupId><artifactId>spring-context</artifactId><version>4.2.6.RELEASE</version></dependency><dependency><grou…...
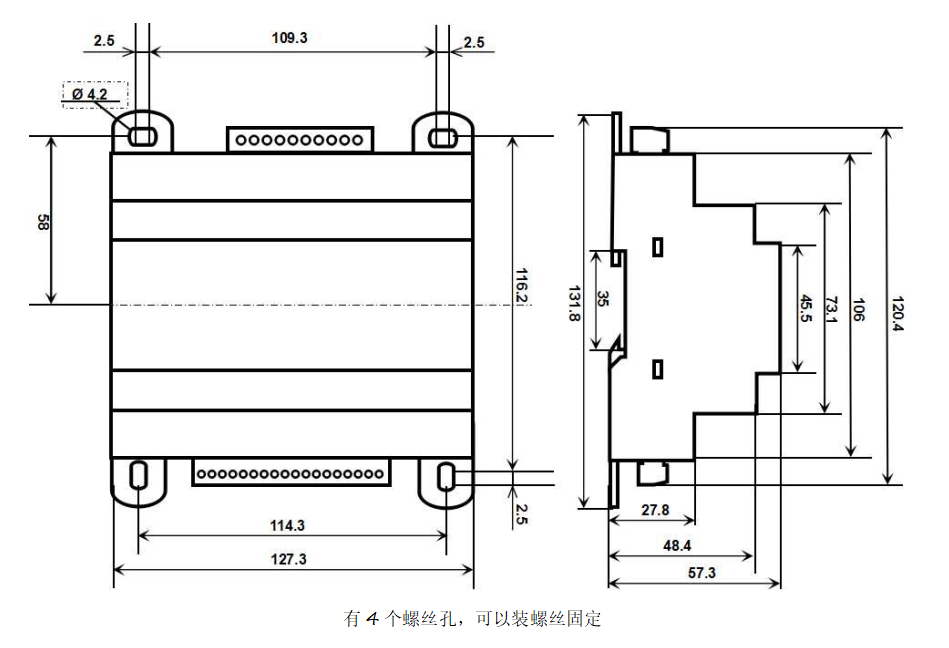
RS232/RS485信号接口转12路模拟信号 隔离D/A转换器LED智能调光控制
特点:● RS-485/232接口,隔离转换成12路标准模拟信号输出● 可选型输出4-20mA或0-10V控制其他设备● 模拟信号输出精度优于 0.2%● 可以程控校准模块输出精度● 信号输出 / 通讯接口之间隔离耐压3000VDC ● 宽电源供电范围:10 ~ 30VDC● 可靠…...

聊一聊代码重构——封装集合和替换算法的代码实践
代码重构相关内容 聊一聊代码重构——我们为什么要代码重构 聊一聊代码重构——代码中究竟存在哪些坏代码 聊一聊代码重构——关于变量的代码实践 聊一聊代码重构——关于循环逻辑的代码实践 聊一聊代码重构——关于条件表达式的代码实践 聊一聊代码重构——程序方法上的…...

FPGA解码4K分辨率4line MIPI视频 OV13850采集 提供工程源码和技术支持
目录1、前言2、Xilinx官方主推的MIPI解码方案3、纯Vhdl方案解码MIPI4、vivado工程介绍5、上板调试验证6、福利:工程代码的获取1、前言 FPGA图像采集领域目前协议最复杂、技术难度最高的应该就是MIPI协议了,MIPI解码难度之高,令无数英雄竞折腰…...
Map接口及遍历方式
1、Map接口实现类的特点1)Map与Collection并列存在。用于保存具有映射关系的数据:Key-Value(无序)2) Map中的key和value可以是任何引用类型的数据,会封装到HashMap$Node对象中3) Map 中的key不允许重复import java.util.HashMap; import java…...

一步步构建自己的前端项目
一、我们先把webpack走通 1、先安装相关依赖,webpack是用来处理命令行参数的,但是我不准备使用webpack-cli,但是还是要求必须安装webpack-cli npm install webapck webpack-cli --save-dev2、npm init -y 3、创建项目结构 build.js cons…...

VMware搭建Mac OS环境
推荐阅读 Proxifier逆向分析(Mac) MacOS Burp2021安装配置 突破iOS App双向认证抓包 App绕过iOS手机的越狱检测 iOS系统抓包入门实践之短链 各种学习环境更新MacOS虚拟机 Android和iOS静态代码扫描工具 iOS系统抓包之短链-破解双向证书 Android和iOS应用源码的静态分析…...
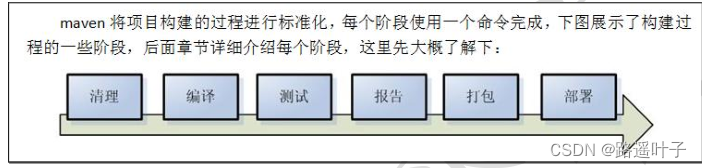
【Maven】什么是Maven?Maven有什么用?
目录 一、什么是 Maven 二、Maven 能解决什么问题 三、Maven 的优势举例 四、Maven 的两个经典作用 4.1 Maven 的依赖管理 4. 2 项目的一键构建 💟 创作不易,不妨点赞💚评论❤️收藏💙一下 一、什么是 Maven Maven 的正确发…...

【JavaSE】类和对象的详解
前言: 大家好,我还是那个不会打拳的程序猿。今天我给大家讲解的是类和对象,相信大家在之前的学习中都是面向过程的思想,那么今天就让我们走向面向对象的世界吧。 目录 1.面向过程VS面向对象 1.1什么是面向过程 1.2什么是面向对…...
2023年中职组“网络安全”赛项广西自治区竞赛任务书
2023年中职组“网络安全”赛项 广西自治区竞赛任务书 一、竞赛时间 总计:360分钟 需求环境可私信博主!点个赞加三连吧! 二、竞赛阶段 竞赛阶段 任务阶段 竞赛任务 竞赛时间 分值 A、B模块 A-1 登录安全加固 180分钟 200分 A-2…...

简单的自定义录屏工具
在csdn上写文章,需要配一些操作动态图,需要针对电脑录屏,可能是整个屏幕录屏,也可能是某窗口,甚至是某一小块区域。 动态图最好是gif格式,方便直接嵌入文章中。 一、设计 窗口类widget 切屏类Capturescr…...

数据结构与算法基础(王卓)(17):KMP算法详解(精讲(最简单、直接、有效的思路方法,答案以及代码原理)
本文具体思路参考: (最后证明,该教材/网课实际上是最有效的) DS第四章【3】KMP1_哔哩哔哩_bilibili 中间走的一些弯路的教材: 第06周05--第4章串、数组和广义表5-4.3串的操作--串的匹配算法2--KMP算法_哔哩哔哩_bi…...
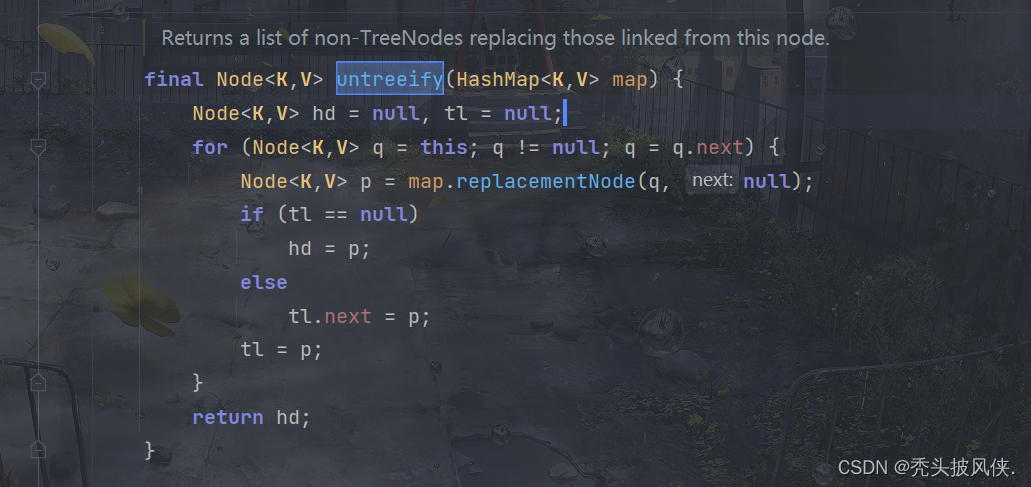
【java基础】HashMap源码解析
文章目录基础说明构造器put方法(无扩容,无冲突)put方法(无冲突,有扩容)put方法(有冲突,无树化)put方法(有冲突,树化)remove方法&#…...

实现异步的8种方式,你知道几个?
一、前言 在编程中,有时候我们需要处理一些费时的操作,比如网络请求、文件读写、数据库操作等等,这些操作会阻塞线程,等待结果返回。为了避免阻塞线程、提高程序的并发处理能力,我们常常采用异步编程。 异步编程是一种…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...
