(枚举)(模拟)(二位前缀和)99. 激光炸弹
目录
题目链接
一些话
切入点
流程
套路
ac代码
题目链接
99. 激光炸弹 - AcWing题库
数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字
数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字
一些话
~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!
切入点
现在有一种新型的激光炸弹,可以摧毁一个包含 R×R 个位置的正方形内的所有目标。
激光炸弹的投放是通过卫星定位的,但其有一个缺点,就是其爆炸范围,即那个正方形的边必须和 x,y 轴平行。
求一颗炸弹最多能炸掉地图上总价值为多少的目标。
1. 求一个矩阵内值的总和,符合二维前缀和的前提条件
2.求符合条件情况的最值,符合枚举的特征
3.写法复杂,条件多,符合模拟的特征
数据范围
0≤R≤1e9
0<N≤10000
0≤Xi,Yi≤5000
0≤Wi≤1000
1. xi,yi<5e3,可能用到双循环枚举
二维数组
流程
1.模拟题,列出伪代码
1.1读题得条件
地图上有 N 个目标,用整数 Xi,Yi, 表示目标在地图上的位置,每个目标都有一个价值 Wi。
注意:不同目标可能在同一位置。
不能直接用cin读值,要先用一个变量储存后再加入这个坐标对应的二维数组里
现在有一种新型的激光炸弹,可以摧毁一个包含 R×R 个位置的正方形内的所有目标。
激光炸弹的投放是通过卫星定位的,但其有一个缺点,就是其爆炸范围,即那个正方形的边必须和 x,y, 轴平行。
可以枚举一个坐标然后直接运算表示矩阵
1.2伪代码:枚举部分
1.2.1确定要枚举什么,如何缩小范围
1.题目要求一个与xy轴平行的矩阵值的总和最值,所以要枚举这个矩阵,矩阵边长是确定的,可以通过枚举一个顶点来表示整个矩阵,用二维前缀和求矩阵总和,只要枚举左上角的顶点然后通过坐标运算就可以表示出右下角的顶点
2.枚举边界超过最大的x,y,r时没有意义,所以只要取x,r,y,r的最大值即可
3.r的范围到1e9,但是x,y最大只有5e3,超过5e3的部分可以直接舍弃,r取5e3+1和r的最小值即可,在确认n,m前进行
1.2.3数据读入部分
题目x,y从0开始,因为要用前缀和,前缀和里有减1的操作,所以读入的坐标要先++才能用
w储存读入的值,然后加入到二维数组
1.2.2前缀和部分
双循环预处理前缀和数组,然后用枚举的坐标查询前缀和,与maxn比较
2.核验数据范围,
1.5e3可以开一个二维数组,
2.答案最多是n*w = 1e7,不用开long long
套路
1.相距为r的坐标的运算
相距为r的两个点a(x1,y1),b(x2,y2)
x2 = x1 + r - 1;
y2 = x2 + r - 1;
2.二维前缀和
//预处理
for(int i = 1;i <= n;i++){for(int j = 1;j <= n;j++){s[i][j] += s[i-1][j] + s[i][j-1] - s[i-1][j-1];}
}
// 查询左上角坐标(x1,y1),右上角坐标(x2,y2)
int res;
res = s[x1][y1] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1];ac代码
// 12:31 - 12 : 41
// 21:39 ~21:42
// 14:45~15:03
// 不能用cin读值,要加等于,x,y+r太大时变小,找最大x,y,r来确定边界
// 枚举左上角得右下角,输出前缀和#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
using namespace std;
const int N = 5e3 + 10;
int n,m,r;
int s[N][N];//5e3+10级别的二维数组开不了longlong,只能开一个数组
int maxn = -0x3f3f3f3f;
int main(){int t;cin >> t >> r;r = min(5001,r);//双循环的最大值,因为要枚举坐标,所以边界不能太大n = m = r;while(t--){int x,y,w;scanf("%d%d%d",&x,&y,&w);x++,y++;s[x][y] += w;n = max(x,n);m = max(y,m);}for(int i = 1;i <= n;i++){for(int j = 1;j <= m;j++){s[i][j] += s[i][j-1] + s[i-1][j] - s[i-1][j-1];}}for(int i = 1;i + r - 1 <= n;i++){for(int j = 1;j + r - 1<= m;j++){maxn = max(maxn,s[i+r-1][j+r-1] - s[i+r-1][j-1] - s[i-1][j+r-1] + s[i-1][j-1]);}}cout << maxn << endl;return 0;
}我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字~
相关文章:
(模拟)(二位前缀和)99. 激光炸弹)
(枚举)(模拟)(二位前缀和)99. 激光炸弹
目录 题目链接 一些话 切入点 流程 套路 ac代码 题目链接 99. 激光炸弹 - AcWing题库 数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字&am…...
vue3+vite项目移动端适配:postcss-pxtorem和amfe-flexible
一,定义 postcss-pxtorem PostCSS 的一个插件,可以从像素单位生成 rem 单位。 amfe-flexible amfe-flexible是配置可伸缩布局方案,主要是将1rem设为viewWidth/10。 二,使用 1. 设置 viewport 在 index.html 中: &l…...

sin x和cos x的导数
我们都知道(sinx)′cosx(\sin x)\cos x(sinx)′cosx,(cosx)′−sinx(\cos x)-\sin x(cosx)′−sinx,但是为什么呢? sinx\sin xsinx的导数 (sinx)′limΔx→0sin(xΔx)−sinxΔx(\sin x)\lim\limits_{\Delta x\rightarrow 0…...

html下自动消失的提示框jQuery实现
引言 最近在找一个可以自动消失的提示框,找来找去,找到了这个:提示框设置_html页面提示框等待一定时间消失博主写得很好,可以直接复制运行出来,我也从中得以受益。本篇文章对这篇博客的代码做了一些小的更新ÿ…...
)
第27篇:Java日期处理总结(一)
目录 1、Date类 1.1 如何实例化Date对象 1.2 Date相关操作方法 1.3 如何获取当前日期...

Linux入门教程——VI/VIM 编辑器
前言 本文小新为大家带来 Linux入门教程——VI/VIM 编辑器 相关知识,具体内容包括VI/VIM是什么,VIM的三种工作模式介绍,包括:一般模式,编辑模式,指令模式,以及模式间转换等进行详尽介绍~ 不积跬…...

第十四届蓝桥杯三月真题刷题训练——第 10 天
目录 第 1 题:裁纸刀 问题描述 运行限制 代码: 第 2 题:刷题统计 问题描述 输入格式 输出格式 样例输入 样例输出 评测用例规模与约定 运行限制 代码: 第 3 题:修建灌木 问题描述 输入格式 输出格式 …...
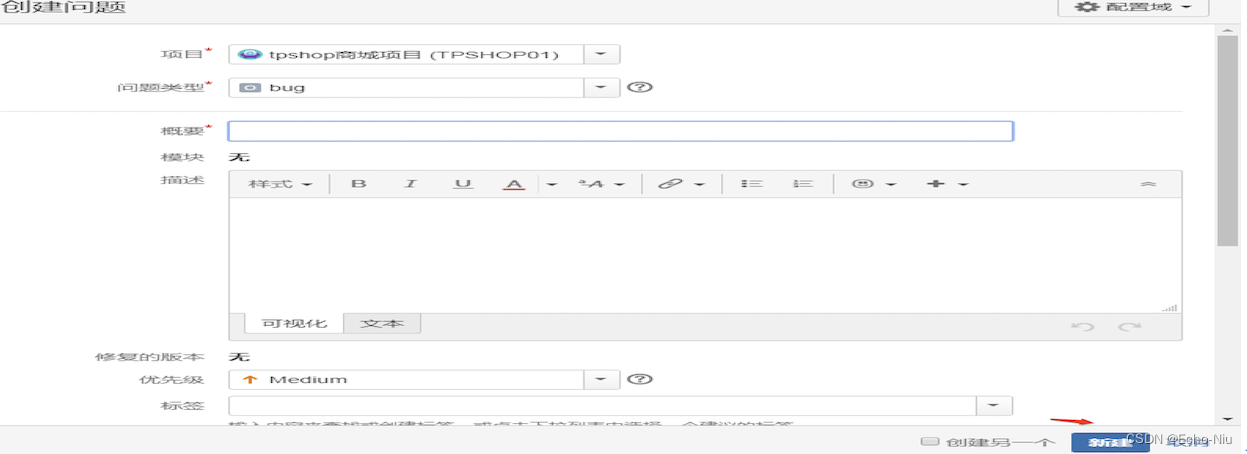
软件测试之jira
Jira 1. Jira 概述 JIRA 是澳大利亚 Atlassian 公司开发的一款优秀的问题跟踪管理软件工具,可以对各种类型的问题进行跟踪管理,包括缺陷、任务、需求、改进等。JIRA采用J2EE技术,能够跨平台部署。它正被广泛的开源软件组织,以及…...

传统方式实现SpringMVC
一、初次尝试SpringMVC 1.1、在pom.xml中添加依赖 <dependency><groupId>org.springframework</groupId><artifactId>spring-context</artifactId><version>4.2.6.RELEASE</version></dependency><dependency><grou…...
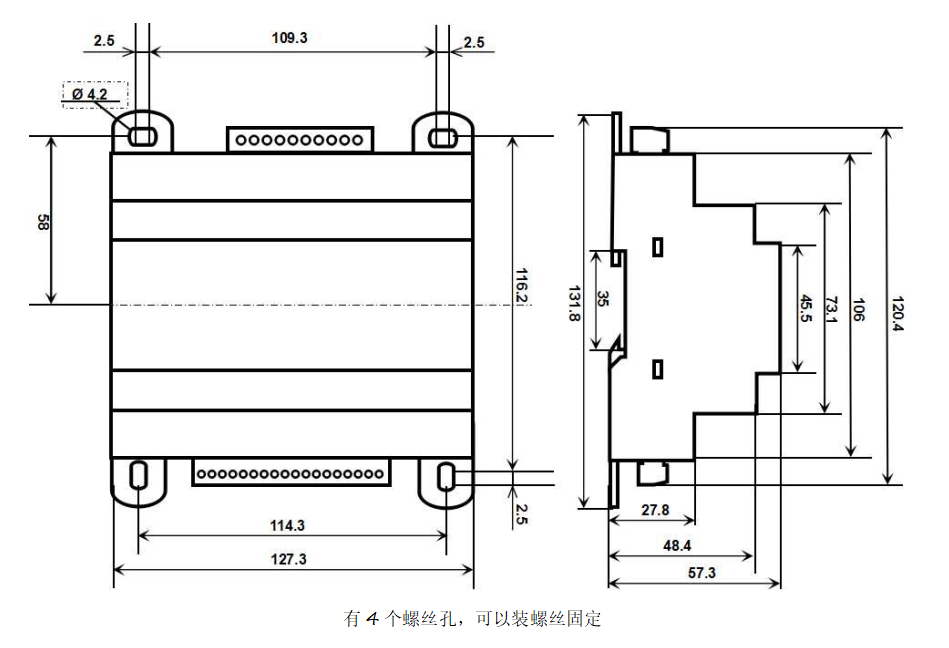
RS232/RS485信号接口转12路模拟信号 隔离D/A转换器LED智能调光控制
特点:● RS-485/232接口,隔离转换成12路标准模拟信号输出● 可选型输出4-20mA或0-10V控制其他设备● 模拟信号输出精度优于 0.2%● 可以程控校准模块输出精度● 信号输出 / 通讯接口之间隔离耐压3000VDC ● 宽电源供电范围:10 ~ 30VDC● 可靠…...

聊一聊代码重构——封装集合和替换算法的代码实践
代码重构相关内容 聊一聊代码重构——我们为什么要代码重构 聊一聊代码重构——代码中究竟存在哪些坏代码 聊一聊代码重构——关于变量的代码实践 聊一聊代码重构——关于循环逻辑的代码实践 聊一聊代码重构——关于条件表达式的代码实践 聊一聊代码重构——程序方法上的…...

FPGA解码4K分辨率4line MIPI视频 OV13850采集 提供工程源码和技术支持
目录1、前言2、Xilinx官方主推的MIPI解码方案3、纯Vhdl方案解码MIPI4、vivado工程介绍5、上板调试验证6、福利:工程代码的获取1、前言 FPGA图像采集领域目前协议最复杂、技术难度最高的应该就是MIPI协议了,MIPI解码难度之高,令无数英雄竞折腰…...
Map接口及遍历方式
1、Map接口实现类的特点1)Map与Collection并列存在。用于保存具有映射关系的数据:Key-Value(无序)2) Map中的key和value可以是任何引用类型的数据,会封装到HashMap$Node对象中3) Map 中的key不允许重复import java.util.HashMap; import java…...

一步步构建自己的前端项目
一、我们先把webpack走通 1、先安装相关依赖,webpack是用来处理命令行参数的,但是我不准备使用webpack-cli,但是还是要求必须安装webpack-cli npm install webapck webpack-cli --save-dev2、npm init -y 3、创建项目结构 build.js cons…...

VMware搭建Mac OS环境
推荐阅读 Proxifier逆向分析(Mac) MacOS Burp2021安装配置 突破iOS App双向认证抓包 App绕过iOS手机的越狱检测 iOS系统抓包入门实践之短链 各种学习环境更新MacOS虚拟机 Android和iOS静态代码扫描工具 iOS系统抓包之短链-破解双向证书 Android和iOS应用源码的静态分析…...
【Maven】什么是Maven?Maven有什么用?
目录 一、什么是 Maven 二、Maven 能解决什么问题 三、Maven 的优势举例 四、Maven 的两个经典作用 4.1 Maven 的依赖管理 4. 2 项目的一键构建 💟 创作不易,不妨点赞💚评论❤️收藏💙一下 一、什么是 Maven Maven 的正确发…...

【JavaSE】类和对象的详解
前言: 大家好,我还是那个不会打拳的程序猿。今天我给大家讲解的是类和对象,相信大家在之前的学习中都是面向过程的思想,那么今天就让我们走向面向对象的世界吧。 目录 1.面向过程VS面向对象 1.1什么是面向过程 1.2什么是面向对…...
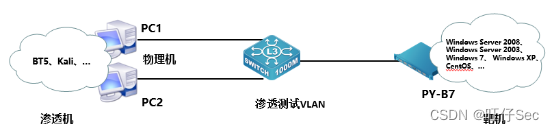
2023年中职组“网络安全”赛项广西自治区竞赛任务书
2023年中职组“网络安全”赛项 广西自治区竞赛任务书 一、竞赛时间 总计:360分钟 需求环境可私信博主!点个赞加三连吧! 二、竞赛阶段 竞赛阶段 任务阶段 竞赛任务 竞赛时间 分值 A、B模块 A-1 登录安全加固 180分钟 200分 A-2…...

简单的自定义录屏工具
在csdn上写文章,需要配一些操作动态图,需要针对电脑录屏,可能是整个屏幕录屏,也可能是某窗口,甚至是某一小块区域。 动态图最好是gif格式,方便直接嵌入文章中。 一、设计 窗口类widget 切屏类Capturescr…...

数据结构与算法基础(王卓)(17):KMP算法详解(精讲(最简单、直接、有效的思路方法,答案以及代码原理)
本文具体思路参考: (最后证明,该教材/网课实际上是最有效的) DS第四章【3】KMP1_哔哩哔哩_bilibili 中间走的一些弯路的教材: 第06周05--第4章串、数组和广义表5-4.3串的操作--串的匹配算法2--KMP算法_哔哩哔哩_bi…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...
