cpp之十大排序算法
十大排序算法
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-riZ9z3wf-1678258189998)(null)]
排序算法的稳定性:在具有多个相同关键字的记录中,若经过排序这些记录的次序保持不变,说排序算法是稳定的。
插入排序O(n2)
-
直接插入排序
动画演示如图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-g8yWt978-1678258189738)(null)]
代码如下:
void Straight_Insertion_Sort(int a[],int length){for (int i = 1;i < length;i++) {if (a[i]<a[i-1]) {int temp = a[i];for (int j = i - 1;j >= 0;j--) {a[j + 1] = a[j];if (a[j] < temp) {a[j + 1] = temp;break;}if (j == 0 && a[j] > temp) {a[j] = temp;}}}}
}
-
折半插入排序
主要分为查找和插入两个部分,图片演示:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NGdwZzKt-1678258189775)(null)]
代码如下:
void Binary_Insert_Sort(int a[],int length) {int low, high, mid;int i, j,temp;for ( i = 1;i < length;i++) {low = 0;high = i - 1;temp = a[i];while (low<=high) {mid = (low + high) / 2;if (temp<a[mid]) {high = mid - 1;}else {low = mid + 1;}}//whilefor ( j = i - 1;j > high;j--) {a[j + 1] = a[j];}a[j + 1] = temp;}//for(i)
冒泡排序O(n2)
思路:两两比较元素,顺序不同就交换
图解:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oaXan5Ej-1678258195664)(null)]
代码:
void Bubble_Sort(int a[],int length) {for (int i = 0;i < length - 1;i++) {for (int j = 0;j <length-i-1 ;j++) {if (a[j]>a[j+1]) {int temp = a[j];a[j] = a[j +1];a[j+1] = temp;}}}
}
选择排序O(n2)
思路:每一次从待排序的数据元素中选择最小(最大)的一个元素作为有序的元素。如果是升序排序,则每次选择最小值就行,这样已经排好序的部分都是生序排序选择排序是不稳定的,比如说(55231这种情况,两个5的相对顺序会变)
图解:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-V6t6QV9b-1678258189910)(null)]
代码:
void Select_Sort(int a[],int length) {for (int i = 0;i < length - 1;i++) {int min_index = i;for (int j = i+1;j < length;j++) {if (a[min_index]>a[j]) {min_index = j;}}//for jif (i!=min_index) {int temp = a[i];a[i] = a[min_index];a[min_index] = temp;}}//for i
}
希尔排序—缩小增量排序O(nlogn)
思路:
希尔排序又叫缩小增量排序,使得待排序列从局部有序随着增量的缩小编程全局有序。当增量为1的时候就是插入排序,增量的选择最好是531这样间隔着的。
其实这个跟选择排序一样的道理,都是不稳定的比如下图7变成9的话,就是不稳定的。
图解:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MFDsQWDw-1678258195700)(null)]
代码:
void Shell_Sort1(int a[], int length) {//首先定义一个初始增量,一般就是数组长度除以2或者3int gap = length / 2;while (gap >= 1) {for (int i = gap;i < length;i++) {int temp = a[i];int j = i;while (j >= gap&&temp<a[j - gap]) {a[j] = a[j - gap];j = j - gap;}//whilea[j] = temp;}//forgap=gap/2;}//while
}
/*****************另一种写法, 好理解****************************/
void shellsort3(int a[], int n)
{int i, j, gap;for (gap = n / 2; gap > 0; gap /= 2)for (i = gap; i < n; i++)/*j>gap之后,j前面的可以重新比较依次保证j前面间隔gap的也是有序的*/for (j = i - gap; j >= 0 && a[j] > a[j + gap]; j -= gap)Swap(a[j], a[j + gap]);
}
快速排序O(nlogn)
思路:快排的核心叫做“基准值“,小于基准值的放在左边,大于基准值的放在右边。然后依次递归。基准值的选取随机的,一般选择数组的第一个或者数组的最后一个,然后又两个指针low和high
图解:基准值就是第一个元素
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oMPzPYDy-1678258195792)(null)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Hd75UZnt-1678258195626)(null)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9cg43CQr-1678258189634)(null)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-C02wROnH-1678258189945)(null)]
1)设置两个变量I、J,排序开始的时候:I=0,J=N-1;
2)以第一个数组元素作为关键数据,赋值给 key ,即 key =A[0];
3)从J开始向前搜索,即由后开始向前搜索(J=J-1即J–),找到第一个小于 key 的值A[j],A[j]与A[i]交换;
4)从I开始向后搜索,即由前开始向后搜索(I=I+1即I++),找到第一个大于 key 的A[i],A[i]与A[j]交换;
5)重复第3、4、5步,直到 I=J; (3,4步是在程序中没找到时候j=j-1,i=i+1,直至找到为止。找到并交换的时候i, j指针位置不变。另外当i=j这过程一定正好是i+或j-完成的最后另循环结束。)
代码:
//快速排序 需要两个函数配合
int Quick_Sort_GetKey(int a[],int low,int high) {int temp = a[low];while (low<high) {//首先比较队尾的元素和关键之temp,如果队尾大指针就往前移动while (low<high&&a[high]>=temp) {high--;}//当a[high]<temp的时候,跳出循环然后将值付给a[low],a[low]=tempa[low] = a[high];//赋值过一次之后就立刻从队首开始比较while (low<high&&a[low]<=temp) {low++;}a[high] = a[low];}//while (low<high)a[low] = temp;//或者a[high]=tempreturn low;
}
void Quick_Sort(int a[],int low,int high) {if (low<high) {int key = Quick_Sort_GetKey(a, low,high);Quick_Sort(a,low,key-1);Quick_Sort(a,key+1,high);}
}
堆排序O(nlogn)
思路:堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。堆排序分为两步:首先将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。随后第二步将其与末尾元素进行交换,此时末尾就为最大值。然后将这个堆结构映射到数组中后,就会变成升序状态了。(即升序—大根堆)
当数组元素映射成为堆时:
- 父结点索引:(i-1)/2
- +左孩子索引:2**i*+1
- 左孩子索引:2**i*+2
图解:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GbqLA5cs-1678258189875)(null)]
基本思想:
- 首先将待排序的数组构造成一个大根堆,此时,整个数组的最大值就是堆结构的顶端
- 将顶端的数与末尾的数交换,此时,末尾的数为最大值,剩余待排序数组个数为n-1
- 将剩余的n-1个数再构造成大根堆,再将顶端数与n-1位置的数交换,如此反复执行,便能得到有序数组
代码:
//index是第一个非叶子节点的下标(根节点)
//递归的方式构建
void Build_Heap(int a[],int length,int index){int left = 2 * index + 1; //index的左子节点int right = 2 * index + 2;//index的右子节点int maxNode = index; //默认当前节点是最大值,当前节点indexif (left<length&&a[left]>a[maxNode]) {maxNode = left;}if (right<length&&a[right]>a[maxNode]) {maxNode = right;}if (maxNode!=index) {int temp = a[maxNode];a[maxNode] = a[index];a[index] = temp;Build_Heap(a,length,maxNode);}}
void Heap_Sort(int a[],int length) {// 构建大根堆(从最后一个非叶子节点向上)//注意,最后一个非叶子节点为(length / 2) - 1for (int i = (length / 2) - 1;i >= 0;i--) {Build_Heap(a, length, i);}for (int i = length - 1;i >= 1;i--) {//交换刚建好的大顶堆的堆顶和堆末尾节点的元素值,int temp = a[i];a[i] = a[0];a[0] = temp;//交换过得值不变,剩下的重新排序成大顶堆Build_Heap(a,i,0);}
}
归并排序(nlogn)
思路:分治思想,将若干个已经排好序的子序合成有序的序列。
图解:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dcYpJuz0-1678258189668)(null)]
代码:
//分治思想,先逐步分解成最小(递归)再合并
//归并
void Merge(int a[],int low,int mid,int high) {int i = low;int j = mid + 1;int k = 0;int *temp = new int[high - low + 1];while (i<=mid&&j<=high) {if (a[i]<=a[j]) {temp[k++] = a[i++];}else {temp[k++] = a[j++];}}//while (i<mid&&j<=high)while (i<=mid) {temp[k++] = a[i++];}while (j<=high) {temp[k++] = a[j++];}for (i = low, k = 0;i <= high;i++, k++) {a[i] = temp[k];}delete[] temp;}
//递归分开
void Merge_Sort(int a[], int low, int high) {if (low < high) {int mid = (low + high) / 2;Merge_Sort(a, low, mid);Merge_Sort(a, mid + 1, high);cout << "mid=" << mid <<" " <<a[mid]<< endl;cout << "low=" << low << " " << a[low] << endl;cout << "high=" << high << " " << a[high] << endl;cout << endl;//递归之后再合并Merge(a, low, mid, high);}
}
代码看不懂没关系,参考链接
计数排序O(n+k)
思路:
将待排序的数据存放到额外开辟的空间中。首先找出元素的最大最小值,然后统计每个元素i出现的次数,然后放入数组i中,数组中存放的是值为i的元素出现的个数。额外数组中第i个元素是待排序数组中值为i的元素的个数。因为要求输入的数有确定范围,同时只能对整数进行排序,有场景限制。
图解:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DpdhUIZI-1678258195743)(null)]
代码:
void Count_Sort(int a[],int length) {//得到待排序的最大值int max = a[0];int i=0;while ( i<length-1) {max = (a[i] > a[i + 1]) ? a[i] : a[i + 1];i++;}int *countArray = new int[max + 1]{0};int *temp = new int[length];for (int i = 0;i < length;i++) {countArray[a[i]]++;}//!!!这一步的思想特别重要,在非比较排序中for (int i = 1;i < max+1;i++) {countArray[i] += countArray[i - 1];}//反向遍历for (int i = length - 1;i >= 0;i--) {temp[countArray[a[i]]-1] = a[i];countArray[a[i]]--;}for (int i = 0;i < length;i++) {a[i] = temp[i];}delete[] countArray;delete[] temp;
}
基数排序O(n x k)
**思路:**基数也就表明桶的个数是定死的,就是10个。基数排序的思想是,从个位依次开始排序,首先按照个位的大小排序,将改变的序列按照十位开始排序,然后依次往后……
图解:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pbKkNGPH-1678258189839)(null)]
代码:
int Get_Max_Digits(int a[],int length) {int max = a[0];int i = 0;while (i<length-1) {max = (a[i] > a[i + 1]) ? a[i] : a[i + 1];i++;}int b = 0;//最大值的位数while (max>0) {max = max / 10;b++;}return b;
}
//切记!桶子只能是十个,是定死的
void Radix_Sort(int b[],int length) {int d = Get_Max_Digits(b, length);//得到最大值的位数int * temp = new int[length];//开辟一个和原数组相同的临时数组//根据最大值的位数进行排序次数循环int radix = 1;for (int i = 0;i < d;i++) {//每次把数据装入桶子前先清空countint count [10] = { 0 }; //计数器 每次循环都清零for (int j = 0;j < length;j++) {//统计尾数为0-9的个数,一次是个十百千....位int tail_number = (b[j]/radix)%10;count[tail_number]++;//每个桶子里面的个数 }//桶中的每一个数的位置一次分配到temp数组中,先找到位置for (int j = 1;j < 10;j++) {count[j] += count[j - 1];}//分配到temp中排序后的位置for (int j = length - 1;j >= 0;j--) {int tail_number = (b[j] / radix) % 10;temp[count[tail_number] - 1] = b[j];count[tail_number]--;}//赋值for (int j = 0;j < length;j++) {b[j] = temp[j];}radix *= 10;}//for(int i)delete[] temp;
}
桶排序O(n+k)
**思路:**基数排序和计数排序都是桶思想的应用。首先要得到整个待排序数组的最大值和最小值,然后设置桶的个数k,这样可以得到每个桶可以放的数的区间。然后遍历待排序的数组,将相关区间内的数放到对应的桶中,这样桶内在排序,就使得整个序列相对有序。
图解:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3Hkv6VD5-1678258189704)(null)]
代码:
void bucketSort(int arr[], int len) {// 确定最大值和最小值int max = INT_MIN; int min = INT_MAX;for (int i = 0; i < len; i++) {if (arr[i] > max) max = arr[i];if (arr[i] < min) min = arr[i];}// 生成桶数组// 设置最小的值为索引0,每个桶间隔为1int bucketLen = max - min + 1;// 初始化桶int bucket[bucketLen];for (int i = 0; i < bucketLen; i++) bucket[i] = 0;// 放入桶中int index = 0;for (int i = 0; i < len; i++) {index = arr[i] - min;bucket[index] += 1;}// 替换原序列int start = 0;for (int i = 0; i < bucketLen; i++) {for (int j = start; j < start + bucket[i]; j++) {arr[j] = min + i;}start += bucket[i];}
}
排序O(n)如何实现
计数排序、基数排序、桶排序。
相关文章:

cpp之十大排序算法
十大排序算法 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-riZ9z3wf-1678258189998)(null)] 排序算法的稳定性:在具有多个相同关键字的记录中,若经过排序这些记录的次序保持不变,说排序算法是稳定的。 插入排序…...
java-正装照换底色小demo-技术分享
文章目录前言java-正装照换底色小demo-技术分享01 实现思路02 效果02::01 原图:02::02 执行单元测试:02::03 效果:03 编码实现前言 如果您觉得有用的话,记得给博主点个赞,评论,收藏一键三连啊,写作不易啊^ _ ^。 而且听说点赞…...
(模拟)(二位前缀和)99. 激光炸弹)
(枚举)(模拟)(二位前缀和)99. 激光炸弹
目录 题目链接 一些话 切入点 流程 套路 ac代码 题目链接 99. 激光炸弹 - AcWing题库 数~啦!我草,又~在~水~字~数~啦!我草,又~在~水~字&am…...
vue3+vite项目移动端适配:postcss-pxtorem和amfe-flexible
一,定义 postcss-pxtorem PostCSS 的一个插件,可以从像素单位生成 rem 单位。 amfe-flexible amfe-flexible是配置可伸缩布局方案,主要是将1rem设为viewWidth/10。 二,使用 1. 设置 viewport 在 index.html 中: &l…...

sin x和cos x的导数
我们都知道(sinx)′cosx(\sin x)\cos x(sinx)′cosx,(cosx)′−sinx(\cos x)-\sin x(cosx)′−sinx,但是为什么呢? sinx\sin xsinx的导数 (sinx)′limΔx→0sin(xΔx)−sinxΔx(\sin x)\lim\limits_{\Delta x\rightarrow 0…...

html下自动消失的提示框jQuery实现
引言 最近在找一个可以自动消失的提示框,找来找去,找到了这个:提示框设置_html页面提示框等待一定时间消失博主写得很好,可以直接复制运行出来,我也从中得以受益。本篇文章对这篇博客的代码做了一些小的更新ÿ…...
)
第27篇:Java日期处理总结(一)
目录 1、Date类 1.1 如何实例化Date对象 1.2 Date相关操作方法 1.3 如何获取当前日期...

Linux入门教程——VI/VIM 编辑器
前言 本文小新为大家带来 Linux入门教程——VI/VIM 编辑器 相关知识,具体内容包括VI/VIM是什么,VIM的三种工作模式介绍,包括:一般模式,编辑模式,指令模式,以及模式间转换等进行详尽介绍~ 不积跬…...

第十四届蓝桥杯三月真题刷题训练——第 10 天
目录 第 1 题:裁纸刀 问题描述 运行限制 代码: 第 2 题:刷题统计 问题描述 输入格式 输出格式 样例输入 样例输出 评测用例规模与约定 运行限制 代码: 第 3 题:修建灌木 问题描述 输入格式 输出格式 …...
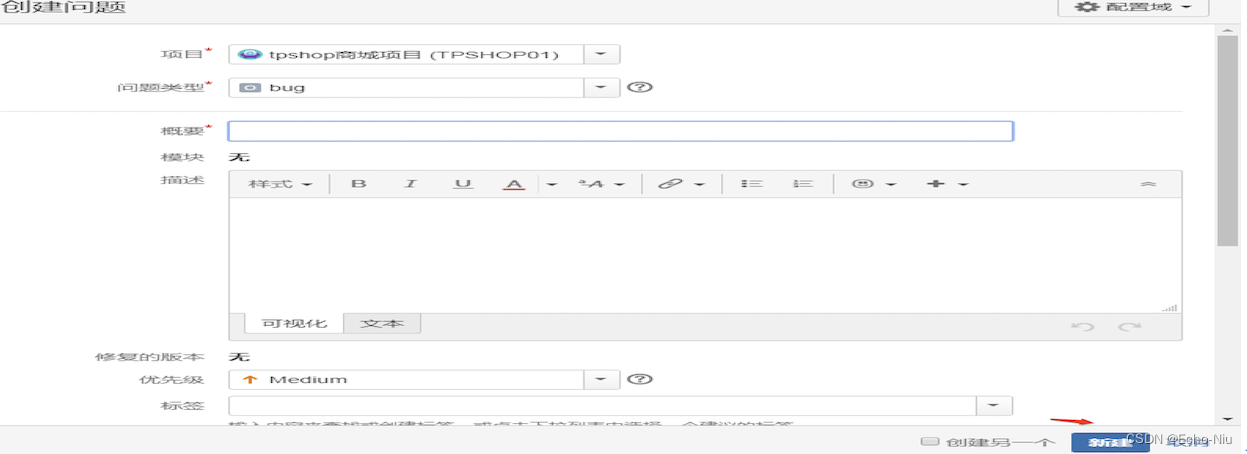
软件测试之jira
Jira 1. Jira 概述 JIRA 是澳大利亚 Atlassian 公司开发的一款优秀的问题跟踪管理软件工具,可以对各种类型的问题进行跟踪管理,包括缺陷、任务、需求、改进等。JIRA采用J2EE技术,能够跨平台部署。它正被广泛的开源软件组织,以及…...

传统方式实现SpringMVC
一、初次尝试SpringMVC 1.1、在pom.xml中添加依赖 <dependency><groupId>org.springframework</groupId><artifactId>spring-context</artifactId><version>4.2.6.RELEASE</version></dependency><dependency><grou…...
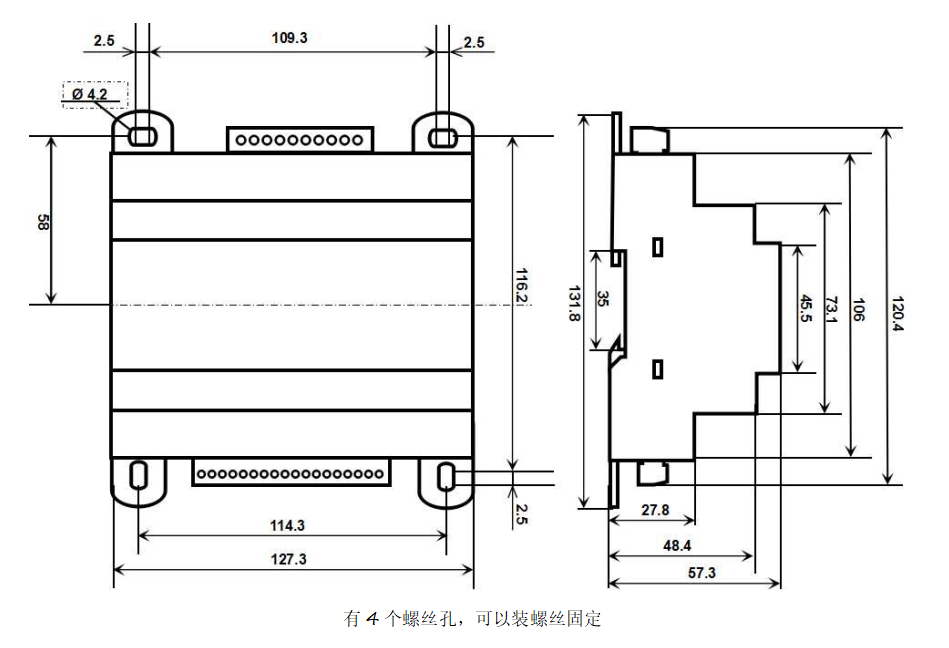
RS232/RS485信号接口转12路模拟信号 隔离D/A转换器LED智能调光控制
特点:● RS-485/232接口,隔离转换成12路标准模拟信号输出● 可选型输出4-20mA或0-10V控制其他设备● 模拟信号输出精度优于 0.2%● 可以程控校准模块输出精度● 信号输出 / 通讯接口之间隔离耐压3000VDC ● 宽电源供电范围:10 ~ 30VDC● 可靠…...

聊一聊代码重构——封装集合和替换算法的代码实践
代码重构相关内容 聊一聊代码重构——我们为什么要代码重构 聊一聊代码重构——代码中究竟存在哪些坏代码 聊一聊代码重构——关于变量的代码实践 聊一聊代码重构——关于循环逻辑的代码实践 聊一聊代码重构——关于条件表达式的代码实践 聊一聊代码重构——程序方法上的…...

FPGA解码4K分辨率4line MIPI视频 OV13850采集 提供工程源码和技术支持
目录1、前言2、Xilinx官方主推的MIPI解码方案3、纯Vhdl方案解码MIPI4、vivado工程介绍5、上板调试验证6、福利:工程代码的获取1、前言 FPGA图像采集领域目前协议最复杂、技术难度最高的应该就是MIPI协议了,MIPI解码难度之高,令无数英雄竞折腰…...
Map接口及遍历方式
1、Map接口实现类的特点1)Map与Collection并列存在。用于保存具有映射关系的数据:Key-Value(无序)2) Map中的key和value可以是任何引用类型的数据,会封装到HashMap$Node对象中3) Map 中的key不允许重复import java.util.HashMap; import java…...

一步步构建自己的前端项目
一、我们先把webpack走通 1、先安装相关依赖,webpack是用来处理命令行参数的,但是我不准备使用webpack-cli,但是还是要求必须安装webpack-cli npm install webapck webpack-cli --save-dev2、npm init -y 3、创建项目结构 build.js cons…...

VMware搭建Mac OS环境
推荐阅读 Proxifier逆向分析(Mac) MacOS Burp2021安装配置 突破iOS App双向认证抓包 App绕过iOS手机的越狱检测 iOS系统抓包入门实践之短链 各种学习环境更新MacOS虚拟机 Android和iOS静态代码扫描工具 iOS系统抓包之短链-破解双向证书 Android和iOS应用源码的静态分析…...
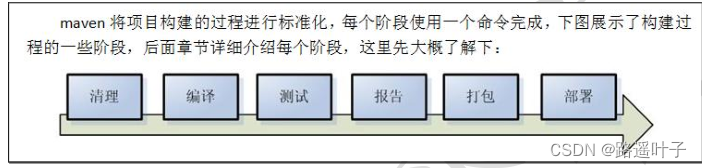
【Maven】什么是Maven?Maven有什么用?
目录 一、什么是 Maven 二、Maven 能解决什么问题 三、Maven 的优势举例 四、Maven 的两个经典作用 4.1 Maven 的依赖管理 4. 2 项目的一键构建 💟 创作不易,不妨点赞💚评论❤️收藏💙一下 一、什么是 Maven Maven 的正确发…...

【JavaSE】类和对象的详解
前言: 大家好,我还是那个不会打拳的程序猿。今天我给大家讲解的是类和对象,相信大家在之前的学习中都是面向过程的思想,那么今天就让我们走向面向对象的世界吧。 目录 1.面向过程VS面向对象 1.1什么是面向过程 1.2什么是面向对…...
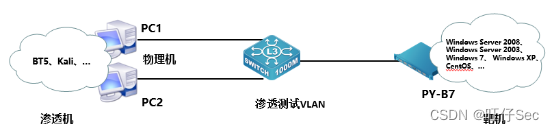
2023年中职组“网络安全”赛项广西自治区竞赛任务书
2023年中职组“网络安全”赛项 广西自治区竞赛任务书 一、竞赛时间 总计:360分钟 需求环境可私信博主!点个赞加三连吧! 二、竞赛阶段 竞赛阶段 任务阶段 竞赛任务 竞赛时间 分值 A、B模块 A-1 登录安全加固 180分钟 200分 A-2…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
