【机器学习】机器学习的重要方法——线性回归算法深度探索与未来展望
欢迎来到 破晓的历程博客


引言
在数据科学日益重要的今天,线性回归算法以其简单、直观和强大的预测能力,成为了众多领域中的基础工具。本文将详细介绍线性回归的基本概念、核心算法,并通过五个具体的使用示例来展示其应用,同时探讨其面临的挑战,并对未来进行展望。
线性回归的基本概念
线性回归是一种预测性建模技术,旨在通过线性方程来描述自变量(X)与因变量(Y)之间的关系。其核心在于找到一个最佳的线性模型,以最小化因变量预测值与实际观测值之间的误差。
线性回归的核心算法
线性回归的核心算法是最小二乘法,它通过最小化误差的平方和来求解最佳的模型参数(即回归系数)。

线性回归的五个使用示例
示例1:房价预测
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression# 假设数据集
data = {'Area': [100, 150, 200, 250, 300, 350, 400, 450, 500, 550],'Price': [200000, 250000, 300000, 350000, 400000, 450000, 500000, 550000, 600000, 650000]
}
df = pd.DataFrame(data)# 划分数据集
X = df[['Area']].values
y = df['Price'].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建并训练模型
model = LinearRegression()
model.fit(X_train, y_train)# 使用模型进行预测(此处省略实际预测结果的展示)

示例2:学生成绩预测
# 假设数据集包含学习时间、复习次数和考试成绩
data = {'StudyHours': [5, 8, 10, 12, 3, 6, 9, 15, 7, 11],'ReviewSessions': [2, 3, 4, 5, 1, 2, 3, 6, 3, 4],'Grade': [75, 85, 90, 95, 60, 70, 80, 98, 75, 88]
}
df = pd.DataFrame(data)# 划分数据集(略去具体步骤,与示例1类似)
# ...# 创建并训练模型(略去具体代码,与示例1类似)
# ...
示例3:销售额预测
# 假设数据集包含广告投入、促销活动次数和销售额
# ...(数据准备和模型训练过程与上述示例类似)
示例4:股票价格预测
# 注意:股票价格预测通常更复杂,可能需要时间序列分析或更高级的模型
# 但为了示例,我们仍假设一个简单的线性关系
# ...(数据准备和模型训练过程)
# 假设数据包含历史股价和交易量等信息
# ...
示例5:天气预测
# 天气预测通常涉及更复杂的模型,如机器学习中的集成方法或深度学习
# 但为了简化,我们假设可以根据历史温度、湿度等线性预测未来温度
# ...(数据准备和模型训练过程)
# 假设数据包含历史气象数据
# ...
注意:由于篇幅和复杂性的限制,示例4和示例5中的具体代码实现被省略了。在实际应用中,这些任务可能需要更复杂的数据处理和模型选择。
线性回归的未来挑战
尽管线性回归在许多领域都取得了成功,但它也面临着一些挑战。首先,现实世界中的关系往往是非线性的,这限制了线性回归的预测能力。为了应对这一挑战,研究者们提出了诸如多项式回归、决策树回归、随机森林回归等更复杂的模型。其次,线性回归对异常值和噪声较为敏感,这可能导致模型性能下降。因此,数据预处理和特征选择成为提高线性回归模型性能的关键步骤。最后,随着大数据时代的到来,如何在海量数据中高效地
相关文章:

【机器学习】机器学习的重要方法——线性回归算法深度探索与未来展望
欢迎来到 破晓的历程博客 引言 在数据科学日益重要的今天,线性回归算法以其简单、直观和强大的预测能力,成为了众多领域中的基础工具。本文将详细介绍线性回归的基本概念、核心算法,并通过五个具体的使用示例来展示其应用,同时探…...

百度云智能媒体内容分析一体机(MCA)建设
导读 :本文主要介绍了百度智能云MCA产品的概念和应用。 媒体信息海量且复杂,采用人工的方式对视频进行分析处理,面临着效率低、成本高的困难。于是,MCA应运而生。它基于百度自研的视觉AI、ASR、NLP技术,为用户提供音视…...

笔记本电脑部署VMware ESXi 6.0系统
正文共:888 字 18 图,预估阅读时间:1 分钟 前面我们介绍了在笔记本上安装Windows 11操作系统(Windows 11升级不了?但Win10就要停服了啊!来,我教你!),也介绍了…...
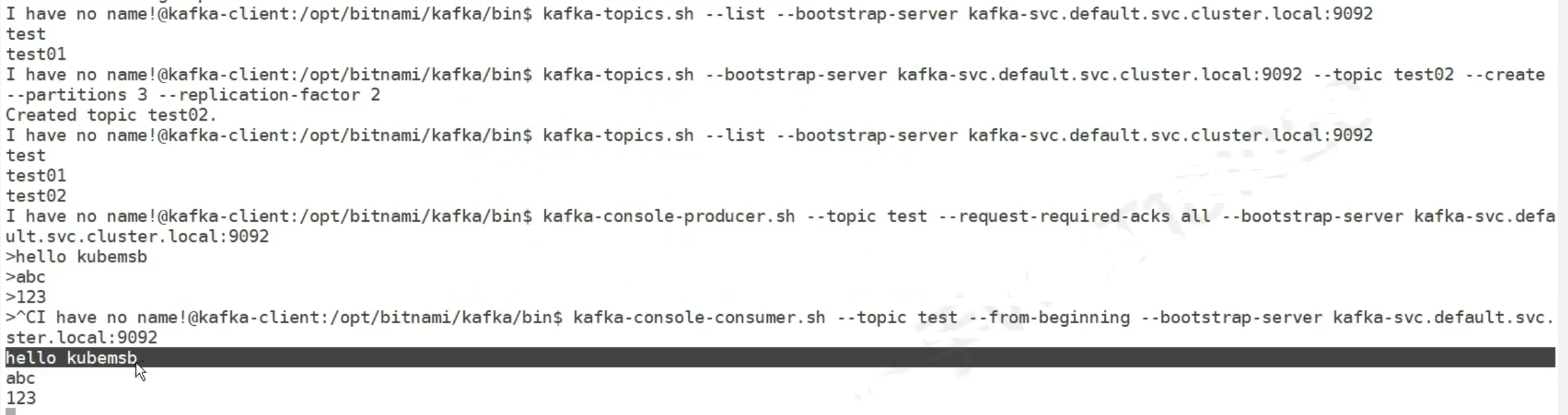
k8s 中间件
1. zookeeper 是的,Zookeeper 和 Kafka 经常一起使用,Zookeeper 在 Kafka 中扮演了关键角色。以下是 Zookeeper 和 Kafka 在实际项目中的结合使用及其作用的详细说明。 项目背景 假设我们有一个分布式数据处理系统,该系统需要高吞吐量的实…...

如何 提升需求确定性
提升需求确定性是确保项目成功的关键之一。以下是一些方法和策略可以帮助你提升需求的确定性: 积极的利益相关者参与: 确保所有关键利益相关者(包括最终用户、业务所有者、开发团队等)参与需求收集和确认过程。他们的参与可以提供…...

探索Sui的面向对象模型和Move编程语言
Sui区块链作为一种新兴的一层协议(L1),采用先进技术来解决常见的一层协议权衡问题。Cointelegraph Research详细剖析了这一区块链新秀。 Sui使用Move编程语言,该语言专注于资产表示和访问控制。本文探讨了Sui的对象中心数据存储模…...

【vue动态组件】VUE使用component :is 实现在多个组件间来回切换
VUE使用component :is 实现在多个组件间来回切换 component :is 动态父子组件传值 相关代码实现: <component:is"vuecomponent"></component>import componentA from xxx; import componentB from xxx; import componentC from xxx;switch(…...
springboot dynamic配置多数据源
pom.xml引入jar包 <dependency><groupId>com.baomidou</groupId><artifactId>dynamic-datasource-spring-boot-starter</artifactId><version>3.5.2</version> </dependency> application配置文件配置如下 需要主要必须配置…...
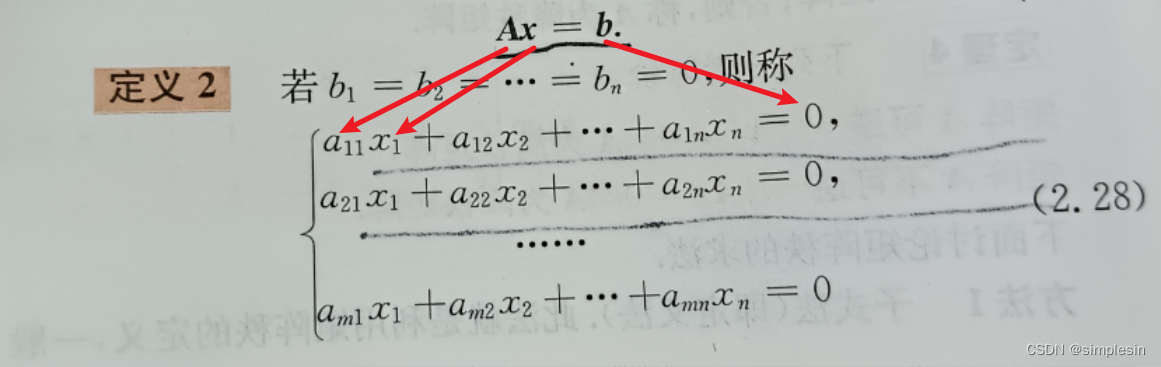
线性代数知识点搜刮
求你别考太细... 目录 异乘变零定理 行列式转置 值不变 重要关系 中间相等,取两头 特征值公式 向量正交 点积为0 拉普拉斯定理 矩阵的秩 特征值和特征向量 |A|特征值的乘积 & tr(A)特征值的和 要记要背 增广矩阵 异乘变零定理 某行(…...

景区智能厕所系统,打造智能化,人性化公共空间
在智慧旅游的大潮中,景区智能厕所系统正逐渐成为提升公共空间智能化、人性化水平的关键载体。作为智慧城市建设的重要组成部分,智能厕所系统不仅解决了传统公厕存在的诸多问题,更通过科技的力量,为游客创造了更加舒适、便捷的如厕…...

Windows中Git的使用(2024最新版)
Windows中Git的使用 获取ssh keys本地绑定邮箱初始化本地仓库添加到本地缓存区提交到本地缓存区切换本地分支为main关联远程分支推送到GitHub查看推送日志 Git 2020年发布了新的默认分支名称"main",取代了"master"作为主分支的名称。操作有了些…...
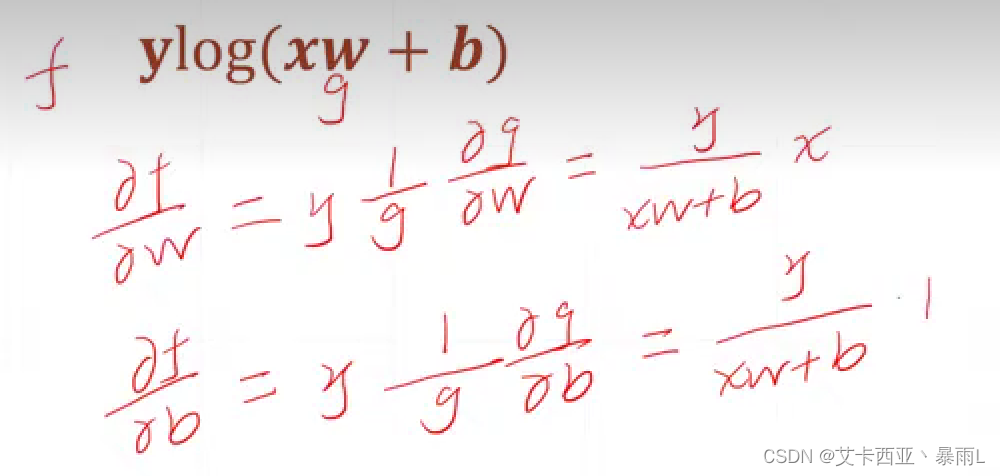
【pytorch12】什么是梯度
说明 导数偏微分梯度 梯度:是一个向量,向量的每一个轴是每一个方向上的偏微分 梯度是有方向也有大小,梯度的方向代表函数在当前点的一个增长的方向,然后这个向量的长度代表了这个点增长的速率 蓝色代表比较小的值,红色…...

南京,协同开展“人工智能+”行动
南京,作为江苏省的省会城市,一直以来都是科技创新和产业发展的高地。近日,南京市政府正式印发了《南京市进一步促进人工智能创新发展行动计划(2024—2026 年)》和《南京市促进人工智能创新发展若干政策措施》的“11”文…...
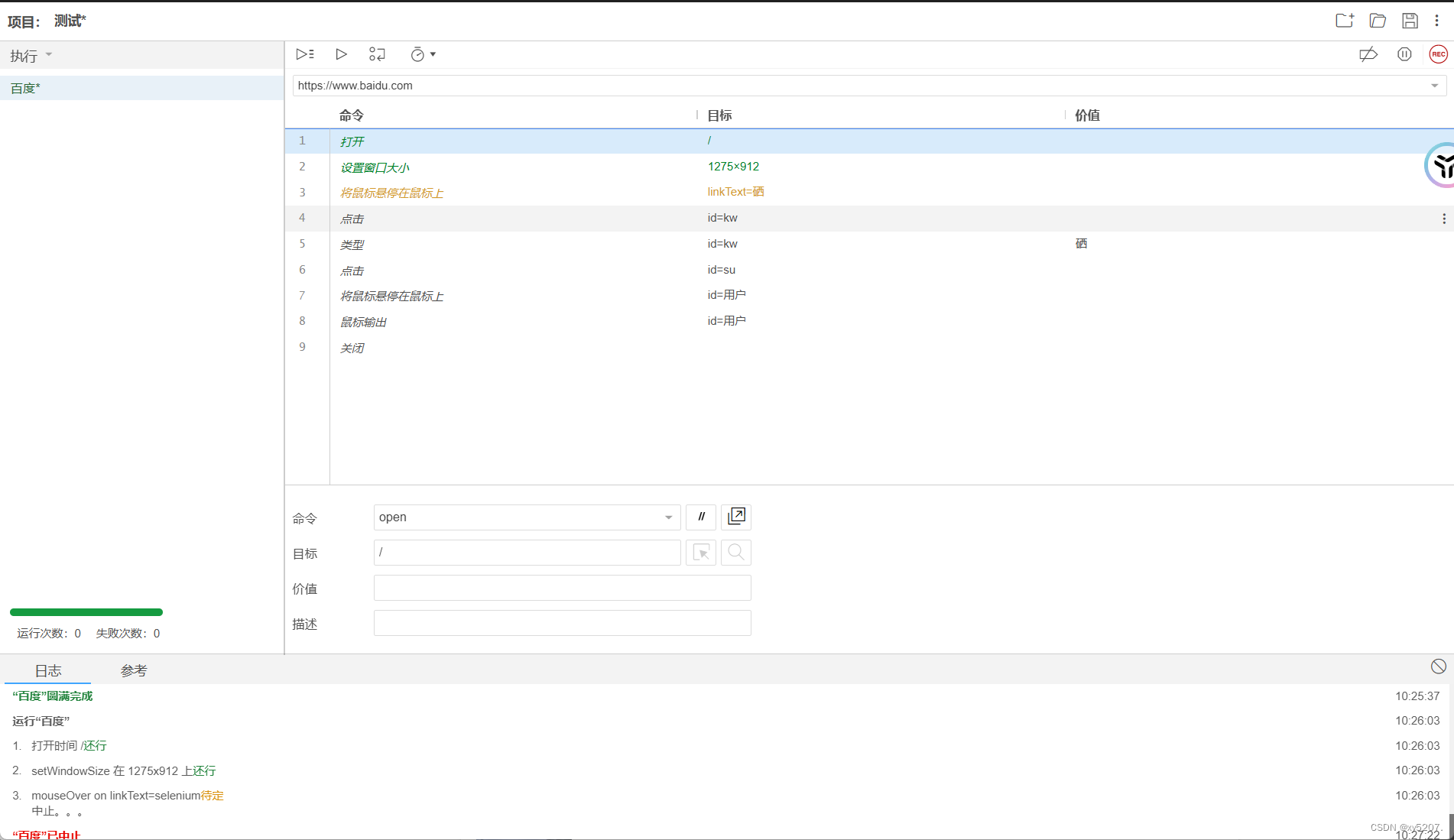
Selenium IDE 的使用指南
Selenium IDE 的使用指南 在自动化测试的领域中,Selenium 是一个广为人知且强大的工具集。而 Selenium IDE 作为其中的一个组件,为测试人员提供了一种便捷且直观的方式来创建和执行自动化测试脚本。 一、Selenium IDE 简介 Selenium IDE 是一个用于录…...

vue配置sql规则
vue配置sql规则 实现效果组件完整代码父组件 前端页面实现动态配置sql条件,将JSON结构给到后端,后端进行sql组装。 这里涉及的分组后端在组装时用括号将这块规则括起来就行,分组的sql连接符(并且/或者)取组里的第一个。…...

面试官:Redis执行lua脚本能保证原子性吗?
核心问题 Redis执行lua脚本是否能确保原子性? 面试经历 面试者在面试中自信回答Redis执行lua脚本能保证原子性,但未能深入解释原因。 原子性概念 原子性:一个事务的所有命令要么全部执行成功,要么全部执行失败。 Redis官方说…...

基于Chrome扩展的浏览器可信事件与网页离线PDF导出
基于Chrome扩展的浏览器可信事件与网页离线PDF导出 Chrome扩展是一种可以在浏览器中添加新功能和修改浏览器行为的软件程序,我们可以基于Manifest规范的API实现对于浏览器和Web页面在一定程度上的修改,例如广告拦截、代理控制等。Chrome DevTools Proto…...
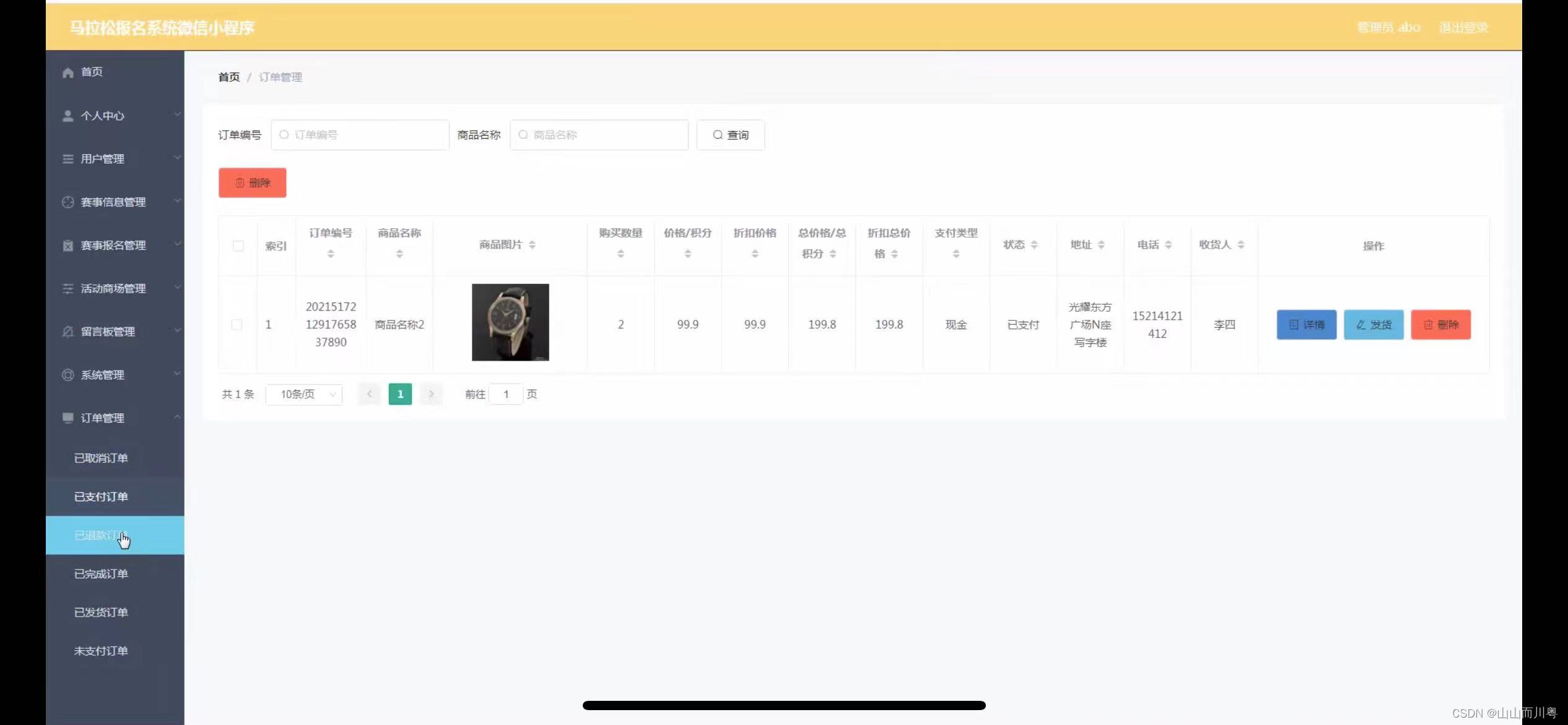
马拉松报名小程序的设计
管理员账户功能包括:系统首页,个人中心,用户管理,赛事信息管理,赛事报名管理,活动商城管理,留言板管理,系统管理 微信端账号功能包括:系统首页,赛事信息&…...
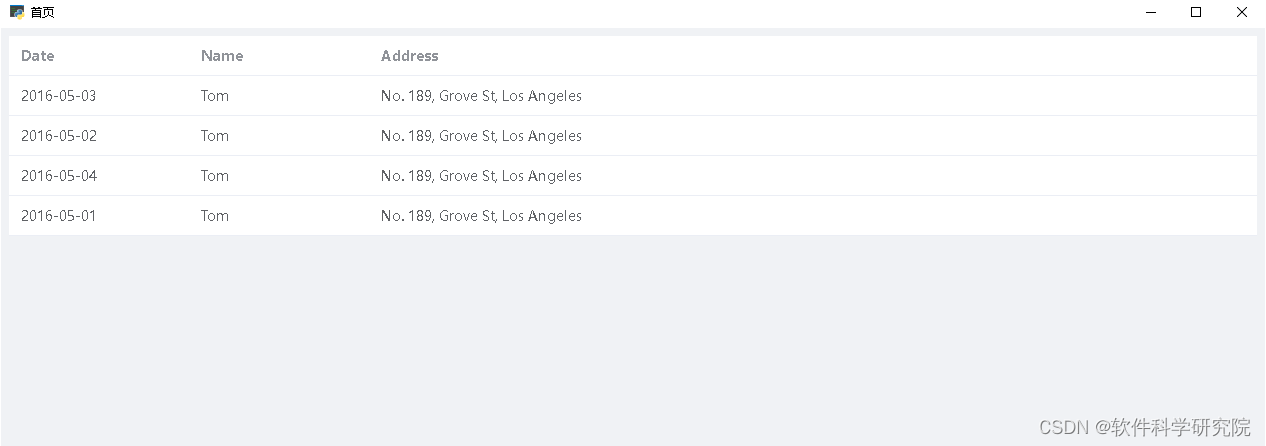
python使用pywebview集成vue3和element-plus开发桌面系统框架
随着web技术越来越成熟,就连QQ的windows客户端都用web技术来开发,所以在未来,web技术来开发windows桌面软件也会越来越多,所以在此发展驱动之下,将最近流程的python与web技术相结合,使用vue3和element-plus…...

C++线程的使用
C11之前,C语言没有对并发编程提供语言级别的支持,这使得我们在编写可移植的并发程序时,存在诸多的不便。现在C11中增加了线程以及线程相关的类,很方便地支持了并发编程,使得编写的多线程程序的可移植性得到了很大的提高…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...
