管理才是最根本的核心竞争力
相信大家对于华为提出的“管理是核心竞争力”“管理才是企业的核心竞争力”等言论并不陌生,而华为的确也一直践行这样的理念。比如,在华为发展历史上很艰难的2002年,华为仍然坚持重点抓管理。总裁任正非后来提到:“2002年华为快崩溃的时候,我们的主题还是抓管理,外界都嘲笑我们”。
任总还提到“单靠技术壁垒取胜的时代很快就要转变为靠管理取胜的时代”,的确技术差距是暂时的,可以通过科学化、高效的管理来缩短这种差距,进而实现超越。当年高通评估华为通信芯片的技术水平,觉得比高通“差3代”,过了两年,认为“差2代”,再过两年,评估“差1代”,又过了两年,认为“已经平起平坐了”!
我们通常认为管理的主要作用是提高效率,我认为:在当今时代,管理的主要目的是加快创新的速度,尤其是产品与技术的创新速度!

但是,管理体系建设的效果体现是比较慢的、逐步的,一般需要相当长时间才能显现出来。当年华为从1996年就开始搞业务流程建设、实施ERP、制定《基本法》、1998年开始引进IPD、2001年开始加强战略管理,到2002年发现与国内两家主要对手(中兴、UT-斯达康)并没有拉开差距,尤其是UT-斯达康似乎势头很猛,大有赶超华为之势。这里背后有华为没有抓住“小灵通”发展机会的原因,但不可否认的是华为花大力气抓管理建设的作用并没有怎么发挥出来。
2003年开始,华为的管理优势就逐步释放出来,而且越来越显著,随着时间的推移,就大大拉开了与对手的差距。中兴还是比较重视管理的,到今天还是一家优秀的企业,只是华为的光环太耀眼了。UT-斯达康经历了爆发期后,管理跟不上,业务转型均以失败告终,早就淡出了通信市场。
的确,华为等一些卓越企业长期发展的历程表明:管理才是最根本的核心竞争力!
相关文章:

管理才是最根本的核心竞争力
相信大家对于华为提出的“管理是核心竞争力”“管理才是企业的核心竞争力”等言论并不陌生,而华为的确也一直践行这样的理念。比如,在华为发展历史上很艰难的2002年,华为仍然坚持重点抓管理。总裁任正非后来提到:“2002年华为快崩…...

Raid阵列中硬盘损坏后,新硬盘可以直接换上吗?
RAID更换的方式基本类似,这里以RAID 1为例。 1. 关闭服务器:确保服务器或RAID控制器处于关闭或已停止状态,以避免数据写入或损坏。确定损坏硬盘:通过RAID控制器的管理界面,确定哪一块硬盘在RAID 中损坏。 2. 拆卸原硬…...

Python爬虫康复训练——笔趣阁《神魂至尊》
还是话不多说,很久没写爬虫了,来个bs4康复训练爬虫,正好我最近在看《神魂至尊》,爬个txt文件下来看看 直接上代码 """ 神魂至尊网址-https://www.bqgui.cc/book/1519/ """ import requests from b…...

Kaptcha验证码
Kaptcha验证码 Kaptcha 是一个用于生成验证码的开源库,在 Java 中使用它可以轻松地为应用程序添加验证码功能。 一、引入依赖 首先,需要在项目的 pom.xml 文件(如果是 Maven 项目)中添加 Kaptcha 的依赖: <depend…...
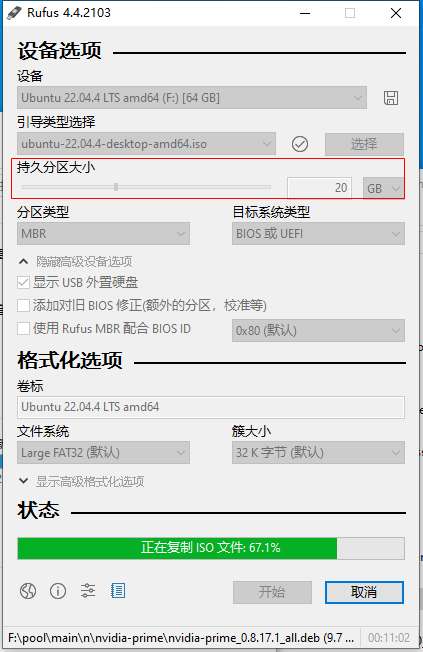
Rufus 制作启动盘 | 便携的工作空间
唠唠闲话 最近服务器硬盘故障多,在修复过程中,学习了一些操作,这里做个记录。本期主要介绍 U盘启动盘的制作,以及持久化存储。 U 盘启动盘 镜像选择 Ubuntu 的版本命名遵循 “Adjective Animal” 的模式,即 “形容…...

python函数参数
Python 函数参数是函数定义时用于接收传递给函数的值的变量。在Python中,函数可以有多种类型的参数,这增加了函数的灵活性和可重用性。下面是一些主要的参数类型: 1. 位置参数(Positional Arguments) 位置参数是最常…...
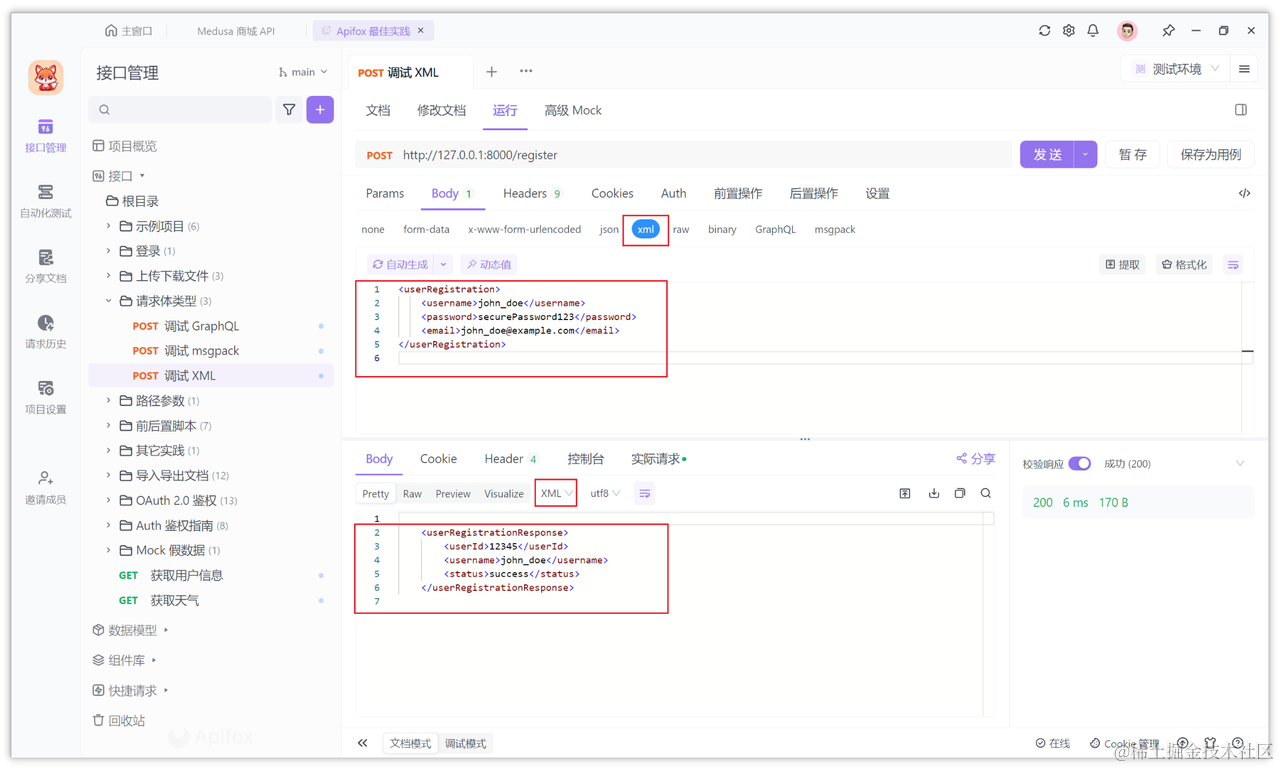
深入理解 XML 和 HTML 之间的区别
在现代网络技术的世界中,XML(可扩展标记语言)和 HTML(超文本标记语言) 是两个非常重要的技术。尽管它们都使用标签和属性的格式来描述数据,但它们在形式和用途上有显著的区别。 概述 什么是 XMLÿ…...

代码随想录算法训练营第四十四天|188.买卖股票的最佳时机IV、309.最佳买卖股票时机含冷冻期、714.买卖股票的最佳时机含手续费
188.买卖股票的最佳时机IV 题目链接:188.买卖股票的最佳时机IV 文档讲解:代码随想录 状态:不会 思路: 在股票买卖1使用一维dp的基础上,升级成二维的即可。 定义dp[k1][2],其中 dp[j][0] 表示第j次交易后持…...

YOLOv8改进 添加CVPR2024 PKINet中注意力机制CAAttention
一、PKINet论文 论文地址:2403.06258 (arxiv.org) 二、CAAttention结构 CAA(Context Anchor Attention)注意力模块是一种用于捕捉长距离上下文信息的并行模块。 在计算机视觉领域中,上下文信息是指与目标物体或任务相关的周围环境和语境信息。上下文信息可以帮助我们更好…...

油猴Safari浏览器插件:Tampermonkey for Mac 下载
Tampermonkey 是一个强大的浏览器扩展,用于运行用户脚本,这些脚本可以自定义和增强网页的功能。它允许用户在网页上执行各种自动化任务,比如自动填写表单、移除广告、改变页面布局等。适用浏览器: Tampermonkey 适用于多数主流浏览…...

如何在Vue中添加事件监听器
在Vue中添加事件监听器主要有两种方式:在模板中直接添加和使用Vue实例的方法。以下将详细解释这两种方法。 1. 在模板中直接添加 在Vue的模板中,你可以直接在HTML元素上使用v-on指令(或其简写形式)来监听DOM事件,并在…...

软设之UML图中的用例图
UML图中用例图 用例图描述一组用例,参与者及它们之间的关系 关系包括: 包含关系,扩展关系,泛化关系 用例建模的流程: 识别参与者 合并需求获得用例 细化用例描述 调整用例模型...

弹性伸缩高性能计算服务一一黑石裸金属服务器
在电商、直播、游戏等业务场景中,对服务器的性能、安全性和稳定性要求尤为苛刻。黑石裸金属服务器作为一种创新的计算服务,以其独特的优势,满足了这些行业对高性能计算服务的迫切需求。本文将详细解析黑石裸金属服务器的优势,并在…...

欢乐钓鱼大师攻略:西沙群岛攻略,内置自动辅助云手机!
《欢乐钓鱼大师》是一款以钓鱼为主题的休闲游戏,玩家可以在虚拟的钓鱼世界中体验真实的钓鱼乐趣,并通过捕捉各种珍稀鱼类来提升自己的钓鱼技能和成就。在这篇攻略中,我们将重点介绍如何在西沙群岛区域有效地捕捉各种典藏鱼类,并提…...
)
Apipost接口测试工具的原理及应用详解(六)
本系列文章简介: 随着软件行业的快速发展,API(应用程序编程接口)作为不同软件组件之间通信的桥梁,其重要性日益凸显。API的质量直接关系到软件系统的稳定性、性能和用户体验。因此,对API进行严格的测试成为…...
)
矩阵的奇异值(Singular Values)
矩阵的奇异值(Singular Values)是奇异值分解(SVD)过程中得到的一组重要特征值。它们在许多应用中非常重要,如信号处理、数据压缩和统计学等。以下是对奇异值及其计算和性质的详细解释: 奇异值分解…...
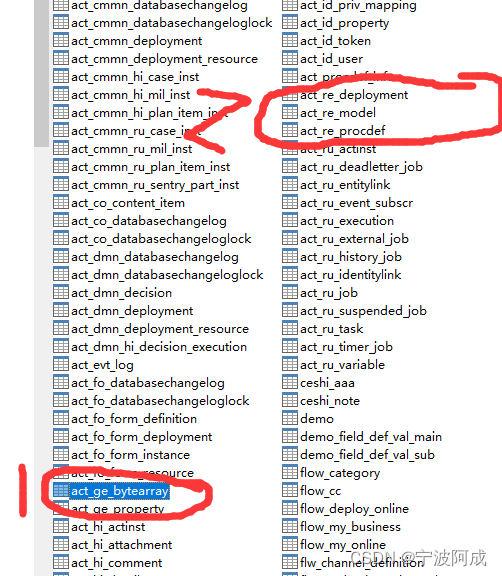
清空flowable的表定义的相关表
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 http://218.75.87.38:9666/ 更多nbcio-boot功能请看演示系统 gitee源代码地址 后端代码: h…...

Tailwind CSS 在vue里 的使用
在Vue项目中使用Tailwind CSS,你需要按照以下步骤操作: 安装Tailwind CSS npm包: npm install -D tailwindcss postcss autoprefixer 使用Tailwind CSS CLI工具创建配置文件: npx tailwindcss init -p 3.在tailwind.config.js中…...

【人工智能】--强化学习(2.0)
个人主页:欢迎来到 Papicatch的博客 课设专栏 :学生成绩管理系统 专业知识专栏: 专业知识 文章目录 🍉强化学习与有监督学习的区别 🍈数据特点 🍈学习目标 🍈反馈机制 🍈策略…...

跟着峰哥学java 微信小程序 第二天 封装ES7 + 后端工作
1.前端 1.1使用promise封装 使用promise封装以至于在图片路径 统一路径中修改 //封装统一请求域名 const baseUrl "http://localhost:8080"; //封装后需导出 export const getBaseUrl()>{return baseUrl; } 导入外来资源 初始化数据 设置数据 将处理后的数据…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
