矩阵的奇异值(Singular Values)
矩阵的奇异值(Singular Values)是奇异值分解(SVD)过程中得到的一组重要特征值。它们在许多应用中非常重要,如信号处理、数据压缩和统计学等。以下是对奇异值及其计算和性质的详细解释:
奇异值分解(SVD)
奇异值分解是矩阵分解的一种方法,它将任意一个实数或复数矩阵分解为三个特定矩阵的乘积。具体来说,对于一个 m × n m \times n m×n的矩阵 M \mathbf{M} M,其奇异值分解表示为:
M = U Σ V ⊤ \mathbf{M} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^\top M=UΣV⊤
其中:
- U \mathbf{U} U是一个 m × m m \times m m×m的正交矩阵,包含了矩阵 M \mathbf{M} M的左奇异向量。
- Σ \mathbf{\Sigma} Σ是一个 m × n m \times n m×n的对角矩阵,对角线上是矩阵 M \mathbf{M} M的奇异值,其余元素为零。
- V ⊤ \mathbf{V}^\top V⊤是一个 n × n n \times n n×n的正交矩阵,包含了矩阵 M \mathbf{M} M的右奇异向量。
奇异值的计算
奇异值 σ i \sigma_i σi是矩阵 M \mathbf{M} M的奇异值分解中对角矩阵 Σ \mathbf{\Sigma} Σ的非负对角元素。它们是 M M ⊤ \mathbf{M} \mathbf{M}^\top MM⊤和 M ⊤ M \mathbf{M}^\top \mathbf{M} M⊤M的非负特征值的平方根。具体来说,如果 M \mathbf{M} M的奇异值为 σ i \sigma_i σi,那么 σ i \sigma_i σi满足以下条件:
M M ⊤ u i = σ i 2 u i \mathbf{M} \mathbf{M}^\top \mathbf{u}_i = \sigma_i^2 \mathbf{u}_i MM⊤ui=σi2ui
M ⊤ M v i = σ i 2 v i \mathbf{M}^\top \mathbf{M} \mathbf{v}_i = \sigma_i^2 \mathbf{v}_i M⊤Mvi=σi2vi
其中, u i \mathbf{u}_i ui和 v i \mathbf{v}_i vi分别是 M M ⊤ \mathbf{M} \mathbf{M}^\top MM⊤和 M ⊤ M \mathbf{M}^\top \mathbf{M} M⊤M的特征向量。
奇异值的性质
- 非负性:奇异值总是非负的,即 σ i ≥ 0 \sigma_i \geq 0 σi≥0。
- 排列顺序:奇异值通常按降序排列,即 σ 1 ≥ σ 2 ≥ ⋯ ≥ σ min ( m , n ) \sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_{\min(m,n)} σ1≥σ2≥⋯≥σmin(m,n)。
- 数量:一个 m × n m \times n m×n矩阵最多有 min ( m , n ) \min(m, n) min(m,n)个奇异值。
- 对称性:奇异值是对称矩阵的特征值的绝对值。
奇异值的应用
奇异值在许多领域都有广泛应用,包括但不限于:
- 矩阵近似:通过截断较小的奇异值,可以得到矩阵的低秩近似,用于数据压缩和降维。
- 数据压缩:在图像处理和压缩中,保留较大的奇异值可以有效减少数据存储量,同时保持较高的数据质量。
- 信号处理:奇异值分解用于去噪和信号恢复。
- 统计学:在主成分分析(PCA)中,奇异值用于确定数据的主成分方向和方差。
通过以上解释,希望能帮助你更好地理解奇异值及其在矩阵分析中的重要性。
好的,让我们通过一个具体的例子来说明奇异值的计算过程。
示例矩阵
考虑一个 2 × 2 2 \times 2 2×2的矩阵 A \mathbf{A} A:
A = ( 3 1 1 3 ) \mathbf{A} = \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix} A=(3113)
计算奇异值
- 计算 A ⊤ A \mathbf{A}^\top \mathbf{A} A⊤A和 A A ⊤ \mathbf{A} \mathbf{A}^\top AA⊤
首先,计算 A ⊤ A \mathbf{A}^\top \mathbf{A} A⊤A和 A A ⊤ \mathbf{A} \mathbf{A}^\top AA⊤:
A ⊤ A = ( 3 1 1 3 ) ⊤ ( 3 1 1 3 ) = ( 10 6 6 10 ) \mathbf{A}^\top \mathbf{A} = \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix}^\top \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix} = \begin{pmatrix} 10 & 6 \\ 6 & 10 \end{pmatrix} A⊤A=(3113)⊤(3113)=(106610)
A A ⊤ = ( 3 1 1 3 ) ( 3 1 1 3 ) ⊤ = ( 10 6 6 10 ) \mathbf{A} \mathbf{A}^\top = \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix} \begin{pmatrix} 3 & 1 \\ 1 & 3 \end{pmatrix}^\top = \begin{pmatrix} 10 & 6 \\ 6 & 10 \end{pmatrix} AA⊤=(3113)(3113)⊤=(106610)
注意到这两个矩阵是相同的。
- 求解 A ⊤ A \mathbf{A}^\top \mathbf{A} A⊤A的特征值
接下来,求解 A ⊤ A \mathbf{A}^\top \mathbf{A} A⊤A的特征值。设 A ⊤ A \mathbf{A}^\top \mathbf{A} A⊤A的特征值为 λ \lambda λ,我们需要解特征方程:
det ( A ⊤ A − λ I ) = 0 \det(\mathbf{A}^\top \mathbf{A} - \lambda \mathbf{I}) = 0 det(A⊤A−λI)=0
即:
det ( 10 − λ 6 6 10 − λ ) = 0 \det\begin{pmatrix} 10 - \lambda & 6 \\ 6 & 10 - \lambda \end{pmatrix} = 0 det(10−λ6610−λ)=0
计算行列式:
( 10 − λ ) 2 − 36 = 0 (10 - \lambda)^2 - 36 = 0 (10−λ)2−36=0
解这个二次方程:
λ 2 − 20 λ + 64 = 0 \lambda^2 - 20\lambda + 64 = 0 λ2−20λ+64=0
求解得到特征值:
λ = 16 和 λ = 4 \lambda = 16 \quad \text{和} \quad \lambda = 4 λ=16和λ=4
- 计算奇异值
奇异值是 A \mathbf{A} A的特征值的平方根。因此:
σ 1 = 16 = 4 \sigma_1 = \sqrt{16} = 4 σ1=16=4
σ 2 = 4 = 2 \sigma_2 = \sqrt{4} = 2 σ2=4=2
因此,矩阵 A \mathbf{A} A的奇异值为 σ 1 = 4 \sigma_1 = 4 σ1=4和 σ 2 = 2 \sigma_2 = 2 σ2=2。
奇异值分解
我们可以进一步进行奇异值分解(SVD),将矩阵 A \mathbf{A} A分解为:
A = U Σ V ⊤ \mathbf{A} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^\top A=UΣV⊤
其中:
- U \mathbf{U} U和 V \mathbf{V} V是正交矩阵(包含左奇异向量和右奇异向量)。
- Σ \mathbf{\Sigma} Σ是对角矩阵,包含奇异值。
对于本例中的矩阵 A \mathbf{A} A:
Σ = ( 4 0 0 2 ) \mathbf{\Sigma} = \begin{pmatrix} 4 & 0 \\ 0 & 2 \end{pmatrix} Σ=(4002)
计算 U \mathbf{U} U和 V \mathbf{V} V
左奇异向量 U \mathbf{U} U和右奇异向量 V \mathbf{V} V是通过求解以下方程得到的:
A A ⊤ u i = σ i 2 u i \mathbf{A} \mathbf{A}^\top \mathbf{u}_i = \sigma_i^2 \mathbf{u}_i AA⊤ui=σi2ui
A ⊤ A v i = σ i 2 v i \mathbf{A}^\top \mathbf{A} \mathbf{v}_i = \sigma_i^2 \mathbf{v}_i A⊤Avi=σi2vi
我们已知:
A A ⊤ = A ⊤ A = ( 10 6 6 10 ) \mathbf{A} \mathbf{A}^\top = \mathbf{A}^\top \mathbf{A} = \begin{pmatrix} 10 & 6 \\ 6 & 10 \end{pmatrix} AA⊤=A⊤A=(106610)
求解这两个矩阵的特征向量即可得到 U \mathbf{U} U和 V \mathbf{V} V。
通过计算,得到:
u 1 = v 1 = ( 1 2 1 2 ) , u 2 = v 2 = ( − 1 2 1 2 ) \mathbf{u}_1 = \mathbf{v}_1 = \begin{pmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{pmatrix}, \quad \mathbf{u}_2 = \mathbf{v}_2 = \begin{pmatrix} -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{pmatrix} u1=v1=(2121),u2=v2=(−2121)
因此:
U = V = ( 1 2 − 1 2 1 2 1 2 ) \mathbf{U} = \mathbf{V} = \begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} U=V=(2121−2121)
综上,矩阵 A \mathbf{A} A的奇异值分解为:
A = U Σ V ⊤ = ( 1 2 − 1 2 1 2 1 2 ) ( 4 0 0 2 ) ( 1 2 1 2 − 1 2 1 2 ) \mathbf{A} = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^\top = \begin{pmatrix} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} \begin{pmatrix} 4 & 0 \\ 0 & 2 \end{pmatrix} \begin{pmatrix} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{pmatrix} A=UΣV⊤=(2121−2121)(4002)(21−212121)
这就是矩阵 A \mathbf{A} A的奇异值计算和奇异值分解的完整过程。
相关文章:
)
矩阵的奇异值(Singular Values)
矩阵的奇异值(Singular Values)是奇异值分解(SVD)过程中得到的一组重要特征值。它们在许多应用中非常重要,如信号处理、数据压缩和统计学等。以下是对奇异值及其计算和性质的详细解释: 奇异值分解…...
清空flowable的表定义的相关表
更多ruoyi-nbcio功能请看演示系统 gitee源代码地址 前后端代码: https://gitee.com/nbacheng/ruoyi-nbcio 演示地址:RuoYi-Nbcio后台管理系统 http://218.75.87.38:9666/ 更多nbcio-boot功能请看演示系统 gitee源代码地址 后端代码: h…...

Tailwind CSS 在vue里 的使用
在Vue项目中使用Tailwind CSS,你需要按照以下步骤操作: 安装Tailwind CSS npm包: npm install -D tailwindcss postcss autoprefixer 使用Tailwind CSS CLI工具创建配置文件: npx tailwindcss init -p 3.在tailwind.config.js中…...

【人工智能】--强化学习(2.0)
个人主页:欢迎来到 Papicatch的博客 课设专栏 :学生成绩管理系统 专业知识专栏: 专业知识 文章目录 🍉强化学习与有监督学习的区别 🍈数据特点 🍈学习目标 🍈反馈机制 🍈策略…...

跟着峰哥学java 微信小程序 第二天 封装ES7 + 后端工作
1.前端 1.1使用promise封装 使用promise封装以至于在图片路径 统一路径中修改 //封装统一请求域名 const baseUrl "http://localhost:8080"; //封装后需导出 export const getBaseUrl()>{return baseUrl; } 导入外来资源 初始化数据 设置数据 将处理后的数据…...

QT学习(6)——QT中的定时器事件,两种实现方式;事件的分发event,事件过滤器
目录 引出定时器事件QTimerEventQTimer 事件的分发事件过滤器 总结QT中的鼠标事件定义QLable的鼠标进入离开事件提升为myLabel重写QLabel的函数鼠标的事件鼠标的左中右键枚举鼠标多事件获取和鼠标移动鼠标追踪 QT中的信号和槽自定义信号和槽1.自定义信号2.自定义槽3.建立连接4.…...

ASP.NET Core 6.0 使用 Action过滤器
Action过滤器 在ASP.NET Core中,Action过滤器用于在执行Action方法之前或之后执行逻辑。你可以创建自定义的Action过滤器来实现这一点。 继承 ActionFilterAttribute 类: [TypeFilter(typeof(CustomAllActionResultFilterAttribute))]public IActionRe…...
Java 并发集合:CopyOnWrite 写时复制集合介绍
大家好,我是栗筝i,这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 016 篇文章,在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验,并希望进…...

Linux 查看修改系统时间| date -s
Linux 查看修改系统时间 date 命令的介绍date基本语法date命令使用示例显示指定条件的时间设置指定条件的时间时间加减操作显示文件最后修改时间显示 UTC 时间 备注 date 命令的介绍 date 命令在 Linux/Unix 系统上的使用。 date 命令可以用于查看和设置系统时间。 date基本语…...

数据库MySQL学习笔记
数据库MySQL学习笔记 主要记录常见的MySQL语句学习过程,增删改查。 -- 显示所有数据库 SHOW DATABASES;-- 创建新数据库 CREATE DATABASE mydatabase;-- 使用数据库 USE mydatabase;-- 显示当前数据库中的所有表 SHOW TABLES;-- 创建新表 CREATE TABLE users (id …...

四端口千兆以太网交换机与 SFP 扩展功能
在数字化时代,网络基础设施的重要性日益凸显,它是企业和个人取得成功的关键支撑。配备 SFP 插槽的 4 端口千兆以太网交换机提供了一种灵活且可扩展的网络解决方案,能够应对快速的数据传输、低延迟以及不断增长的带宽需求。本篇文章深入探讨了…...

Renderless 思想正在影响前端开发
本文由前端小伙伴方长_beezen 原创。欢迎大家踊跃投稿。 原文链接:https://juejin.cn/post/7385752495535472655 前言 截止到 2024 年,跨端应用开发所需要考虑的兼容性,已经涵盖了框架、平台和设备类型等多个方面,例如࿱…...
maven 打包执行配置(对maven引用的包或者丢进去的包都包含在里面)打成jar包
一 、springboot jar包 maven的pom文件 1 在resources下放了一些文件想打进去jar包 2 在lib下放了其他稀奇古怪jar包文件想打进去jar包 编写如下引入jar <build><!-- 打包名称 --><finalName>${project.artifactId}</finalName><resources><…...

Python酷库之旅-第三方库Pandas(004)
目录 一、用法精讲 5、pandas.DataFrame.to_csv函数 5-1、语法 5-2、参数 5-3、功能 5-4、返回值 5-5、说明 5-6、用法 5-6-1、代码示例 5-6-2、结果输出 6、pandas.read_fwf函数 6-1、语法 6-2、参数 6-3、功能 6-4、返回值 6-5、说明 6-6、用法 6-6-1、代码…...

天猫超市卡怎么用
猫超卡是在天猫超市里面消费用的卡 但是我们现在买东西都喜欢货比三家,肯定是哪家划算在哪买,要是淘宝其他店铺或京东卖的更便宜,猫超卡自然就用不上了 这种情况的话,还不如直接把猫超卡的余额提出来,买东西也不受限…...

ai智能语音机器人电销系统:让销售更快速高效
智能机器人电销系统是指采用人工智能和机器人技术来实现的自动电销工具。随着企业竞争加剧,销售团队面临的挑战也越来越大。在人力资源和成本控制方面有很大的限制,而传统的电销方式也已经无法满足市场需求,因此需要一种新的解决方案来提高营…...

Redis 中的通用命令(命令的返回值、复杂度、注意事项及操作演示)
Redis 中的通用命令(高频率操作) 文章目录 Redis 中的通用命令(高频率操作)Redis 的数据类型redis-cli 命令Keys 命令Exists 命令Expire 命令Ttl 命令Type命令 Redis 的数据类型 Redis 支持多种数据类型,整体来说,Redis 是一个键值对结构的,…...

【Hive实战】 HiveMetaStore的指标分析
HiveMetaStore的指标分析(一) 文章目录 HiveMetaStore的指标分析(一)背景目标部署架构 hive-site.xml相关配置元数据服务的指标相关配置 源码部分(hive2.3系)JvmPauseMonitor.javaHiveMetaStore的内部类HMS…...

【Linux系统】CUDA的安装与graspnet环境配置遇到的问题
今天在安装环境时遇到报错: The detected CUDA version (10.1) mismatches the version that was used to compile PyTorch (11.8). Please make sure to use the same CUDA versions. 报错原因:安装的cuda版本不对应,我需要安装cuda的版本…...
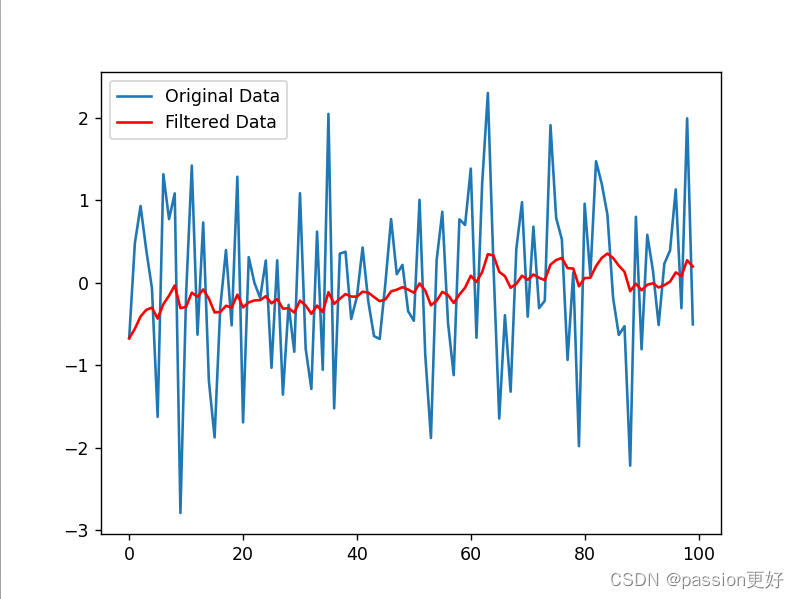
滤波算法学习笔记
目录 引言 一、定义 二、分类 三、常见滤波算法 四、应用与优势 五、发展趋势 例程 1. 均值滤波(Moving Average Filter) 2. 中值滤波(Median Filter) 3. 高斯滤波(Gaussian Filter) 4.指数移动…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
