滤波算法学习笔记
目录
引言
一、定义
二、分类
三、常见滤波算法
四、应用与优势
五、发展趋势
例程
1. 均值滤波(Moving Average Filter)
2. 中值滤波(Median Filter)
3. 高斯滤波(Gaussian Filter)
4.指数移动平均滤波(Exponential Moving Average Filter)
引言
滤波算法是一种数学技术,广泛应用于信号处理和图像处理领域,旨在通过特定的算法对信号的频谱特性进行处理,以达到去噪、平滑、增强或分析信号的目的。以下是对滤波算法的详细概述:
一、定义
滤波(Wave filtering)是将信号中特定波段频率滤除的操作,是抑制和防止干扰的一项重要措施。滤波算法的目的是从原始有干扰的测量数据中提取出有用信号,或者对信号进行某种特定的处理以改善其质量。
二、分类
滤波算法可以根据不同的标准进行分类,常见的分类方式包括:
- 按动力学系统的线性或非线性特征分类:
- 线性滤波:如最小二乘估计法、维纳滤波法、卡尔曼滤波法等,这类算法基于线性系统理论,适用于线性系统或可近似为线性系统的场景。
- 非线性滤波:如扩展卡尔曼滤波算法、无迹卡尔曼滤波算法、粒子滤波算法等,这类算法能够处理非线性系统,具有更高的灵活性和适应性。
- 按系统的不同噪声特性分类:
- 高斯白噪声滤波:针对噪声符合高斯分布且功率谱密度在整个频域内均匀分布的情况设计的滤波算法。
- 非高斯白噪声滤波:针对噪声不符合高斯分布或功率谱密度不均匀的情况设计的滤波算法。
三、常见滤波算法
-
维纳滤波:一种基于最小均方误差准则的线性滤波算法,适用于平稳随机过程的滤波和预测问题。维纳滤波公式是通过平稳过程的谱分解导出的,但在实际应用中受到一定限制。
-
卡尔曼滤波:一种高效的递推滤波算法,适用于线性动态系统的状态估计。卡尔曼滤波通过预测和更新两个步骤不断迭代,以实现对系统状态的实时估计。
-
中值滤波:一种常用的非线性滤波算法,在图像处理中尤为常见。中值滤波通过选择待处理像素邻域内各像素值的中值来代替待处理像素值,从而消除噪声并保护图像边缘信息。
-
高斯滤波:一种线性平滑滤波算法,适用于消除高斯噪声。高斯滤波通过对整幅图像进行加权平均处理,使图像中的每个像素值都由其邻域内的像素值加权平均后得到。
-
其他滤波算法:还包括限幅滤波、算术平均滤波、滑动窗口滤波、防脉冲干扰平均滤波、一阶滞后滤波、加权递推平均滤波、消抖滤波等多种算法,它们各自具有不同的特点和适用范围。
四、应用与优势
滤波算法在信号处理和图像处理领域具有广泛的应用,如通信、雷达、声纳、自动控制、图像处理、生物医学工程等领域。滤波算法的优势在于能够有效地抑制噪声、提高信号质量、提取有用信息等,从而改善系统的性能和可靠性。
五、发展趋势
随着计算机技术的不断发展和算法的不断优化,滤波算法也在不断演进。未来的滤波算法将更加智能化、自适应化,能够更好地应对复杂多变的信号处理需求。同时,随着大数据和人工智能技术的兴起,滤波算法也将与这些先进技术相结合,为信号处理领域带来更多的创新和发展机遇。
例程
1. 均值滤波(Moving Average Filter)
均值滤波是一种简单的线性滤波,通过计算数据点周围一定范围内的平均值来平滑数据。
工作原理:
- 选择一个窗口大小(滤波器长度)。
- 将窗口沿着数据序列滑动。
- 在每个位置上,计算窗口内所有数据点的平均值。
- 将计算出的平均值作为该位置滤波后的结果。
优点:
- 实现简单。
- 对随机噪声有很好的抑制效果。
缺点:
- 可能导致信号边缘模糊。
- 不适用于非平稳信号。
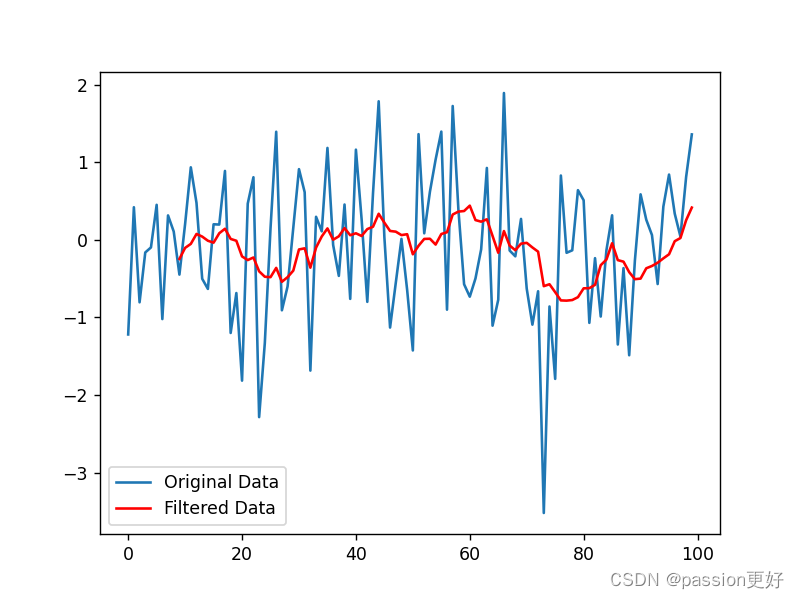
import numpy as npdef moving_average(x, window_size):ret = np.cumsum(x, dtype=float)ret[window_size:] = ret[window_size:] - ret[:-window_size]return ret[window_size - 1:] / window_size# 示例数据
data = np.random.randn(100)
window_size = 10
filtered_data = moving_average(data, window_size)# 可视化
import matplotlib.pyplot as pltplt.plot(data, label='Original Data')
plt.plot(np.arange(window_size - 1, len(data)), filtered_data, label='Filtered Data', color='r')
plt.legend()
plt.show()2. 中值滤波(Median Filter)
中值滤波是一种非线性滤波技术,它将每个数据点替换为其邻域内的中位数,对于去除椒盐噪声特别有效。
工作原理:
- 选择一个窗口大小。
- 将窗口沿着数据序列滑动。
- 在每个位置上,对窗口内的数据点进行排序。
- 选取排序后的中位数作为该位置滤波后的结果。
优点:
- 对椒盐噪声有很好的抑制效果。
- 能够较好地保持信号的边缘信息。
缺点:
- 对高斯噪声的抑制效果不如均值滤波和高斯滤波。
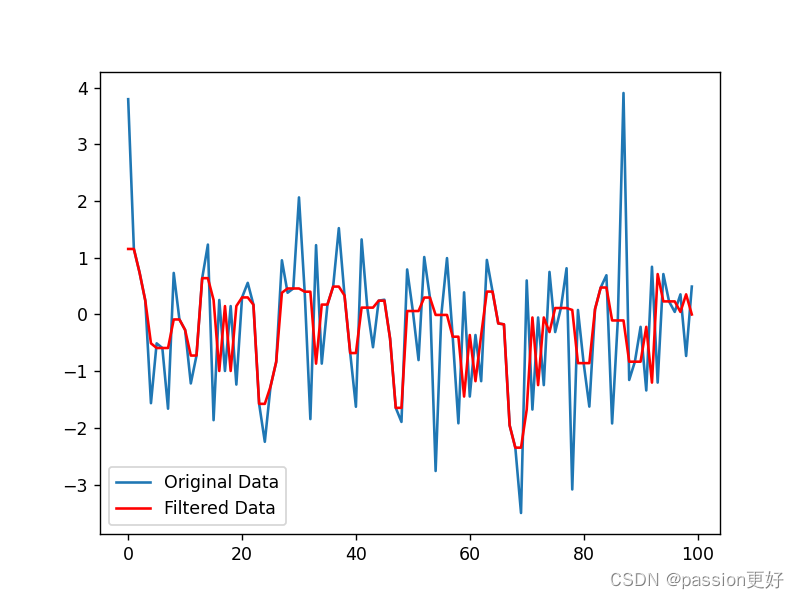
from scipy.signal import medfilt
import numpy as np
import matplotlib.pyplot as plt# 示例数据
data = np.random.randn(100)
# 添加一些噪声
data[np.random.choice(np.arange(len(data)), 10, replace=False)] = np.random.uniform(low=-5, high=5, size=10)# 应用中值滤波
filtered_data = medfilt(data, kernel_size=3)# 可视化
plt.plot(data, label='Original Data')
plt.plot(filtered_data, label='Filtered Data', color='r')
plt.legend()
plt.show()3. 高斯滤波(Gaussian Filter)
高斯滤波是一种线性平滑滤波,其权重由高斯函数给出。这种方法适用于去除高斯噪声,同时能够在一定程度上保持信号的细节信息。
工作原理:
- 选择一个高斯核(即高斯函数的离散形式),该核的大小和标准差决定了滤波的平滑程度。
- 将高斯核沿着数据序列(或图像)滑动。
- 在每个位置上,计算高斯核与对应数据点(或像素)的加权和。
- 将加权和作为该位置滤波后的结果。
优点:
- 对高斯噪声有很好的抑制效果。
- 能够在一定程度上保持信号的细节信息。
缺点:
- 相对于均值滤波,计算量较大。
- 如果标准差选择不当,可能导致信号过平滑或细节丢失。
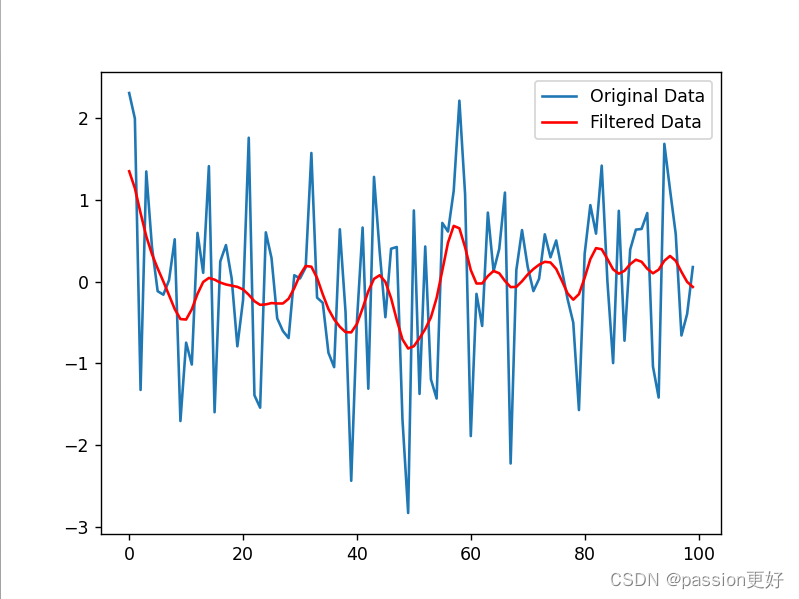
import numpy as np
import matplotlib.pyplot as pltfrom scipy.ndimage import gaussian_filter# 示例数据
data = np.random.randn(100)# 应用高斯滤波
sigma = 2 # 标准差
filtered_data = gaussian_filter(data, sigma=sigma)# 可视化
plt.plot(data, label='Original Data')
plt.plot(filtered_data, label='Filtered Data', color='r')
plt.legend()
plt.show()4.指数移动平均滤波(Exponential Moving Average Filter)
指数移动平均滤波(是一种在信号处理中广泛应用的加权移动平均滤波技术。它通过对历史数据进行加权平均,并赋予较新数据点更高的权重,从而实现对时间序列数据的平滑处理。
工作原
- 加权机制:与简单的移动平均滤波(等权重平均)不同,EWMA采用指数衰减的方式对历史数据进行加权平均。即较新的数据点具有更高的权重,而较旧的数据点权重逐渐降低。
- 迭代计算:每次新的数据点到来时,都会根据当前的平滑系数(α)和前一时刻的输出值(Y_{n-1})以及当前输入值(X_n)来计算新的输出值(Y_n)。这种迭代计算方式使得EWMA能够动态地适应数据的变化。
优点
- 快速响应:由于较新数据点具有更高的权重,EWMA能够更快地捕捉到数据的变化趋势,对于实时性要求较高的应用场景尤为适用。
- 灵活性:通过调整平滑系数(α),可以灵活地控制滤波器的响应速度和平滑程度。较大的α值会使滤波器更快地响应数据变化,而较小的α值则会使滤波器更加平滑。
- 稳定性:虽然EWMA对数据的快速变化敏感,但其加权机制也确保了滤波器在数据相对稳定时能够保持较好的平滑效果,减少噪声对数据的影响。
缺点
- 滞后性:尽管EWMA比简单移动平均滤波具有更快的响应速度,但在极端情况下(如数据发生突变时),它仍然可能存在一定的滞后性。这是因为平滑系数的选择需要在响应速度和平滑程度之间做出权衡。
- 参数敏感性:平滑系数(α)的选择对滤波器的性能具有重要影响。如果α选择不当,可能会导致滤波器过度平滑或响应不足。因此,在实际应用中需要根据具体情况仔细调整该参数。
- 计算复杂度:虽然EWMA的计算过程相对简单,但在处理大规模数据时,其迭代计算方式可能会增加计算复杂度。特别是在实时系统中,需要确保计算速度能够满足应用需求。
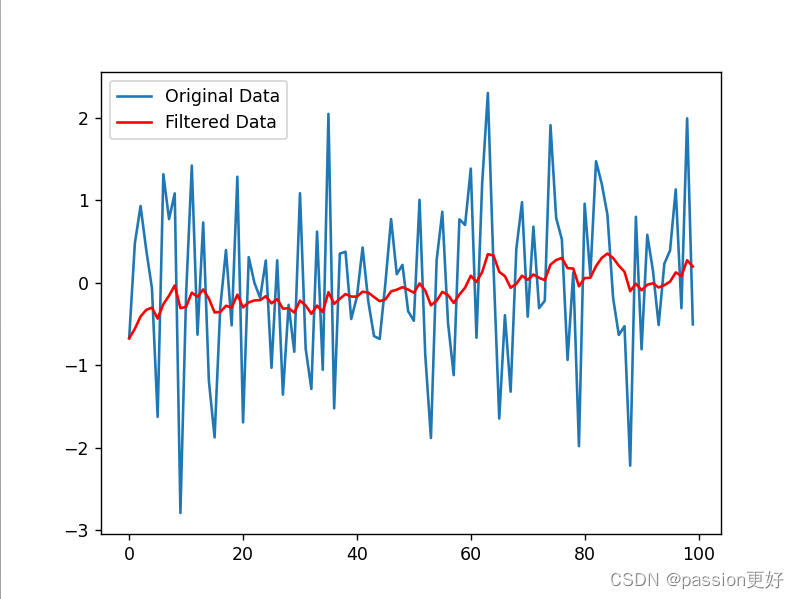
import numpy as np
def exponential_moving_average(data, alpha):"""计算指数移动平均滤波。参数:data -- 输入数据,numpy数组。alpha -- 平滑系数,介于0和1之间。返回:filtered_data -- 滤波后的数据,numpy数组。"""result = np.zeros_like(data)result[0] = data[0]for n in range(1, len(data)):result[n] = alpha * data[n] + (1 - alpha) * result[n - 1]return result# 示例数据
data = np.random.randn(100)
alpha = 0.1
filtered_data = exponential_moving_average(data, alpha)# 可视化
import matplotlib.pyplot as pltplt.plot(data, label='Original Data')
plt.plot(filtered_data, label='Filtered Data', color='r')
plt.legend()
plt.show()相关文章:

滤波算法学习笔记
目录 引言 一、定义 二、分类 三、常见滤波算法 四、应用与优势 五、发展趋势 例程 1. 均值滤波(Moving Average Filter) 2. 中值滤波(Median Filter) 3. 高斯滤波(Gaussian Filter) 4.指数移动…...
【机器学习】机器学习的重要方法——线性回归算法深度探索与未来展望
欢迎来到 破晓的历程博客 引言 在数据科学日益重要的今天,线性回归算法以其简单、直观和强大的预测能力,成为了众多领域中的基础工具。本文将详细介绍线性回归的基本概念、核心算法,并通过五个具体的使用示例来展示其应用,同时探…...

百度云智能媒体内容分析一体机(MCA)建设
导读 :本文主要介绍了百度智能云MCA产品的概念和应用。 媒体信息海量且复杂,采用人工的方式对视频进行分析处理,面临着效率低、成本高的困难。于是,MCA应运而生。它基于百度自研的视觉AI、ASR、NLP技术,为用户提供音视…...

笔记本电脑部署VMware ESXi 6.0系统
正文共:888 字 18 图,预估阅读时间:1 分钟 前面我们介绍了在笔记本上安装Windows 11操作系统(Windows 11升级不了?但Win10就要停服了啊!来,我教你!),也介绍了…...
k8s 中间件
1. zookeeper 是的,Zookeeper 和 Kafka 经常一起使用,Zookeeper 在 Kafka 中扮演了关键角色。以下是 Zookeeper 和 Kafka 在实际项目中的结合使用及其作用的详细说明。 项目背景 假设我们有一个分布式数据处理系统,该系统需要高吞吐量的实…...

如何 提升需求确定性
提升需求确定性是确保项目成功的关键之一。以下是一些方法和策略可以帮助你提升需求的确定性: 积极的利益相关者参与: 确保所有关键利益相关者(包括最终用户、业务所有者、开发团队等)参与需求收集和确认过程。他们的参与可以提供…...

探索Sui的面向对象模型和Move编程语言
Sui区块链作为一种新兴的一层协议(L1),采用先进技术来解决常见的一层协议权衡问题。Cointelegraph Research详细剖析了这一区块链新秀。 Sui使用Move编程语言,该语言专注于资产表示和访问控制。本文探讨了Sui的对象中心数据存储模…...

【vue动态组件】VUE使用component :is 实现在多个组件间来回切换
VUE使用component :is 实现在多个组件间来回切换 component :is 动态父子组件传值 相关代码实现: <component:is"vuecomponent"></component>import componentA from xxx; import componentB from xxx; import componentC from xxx;switch(…...
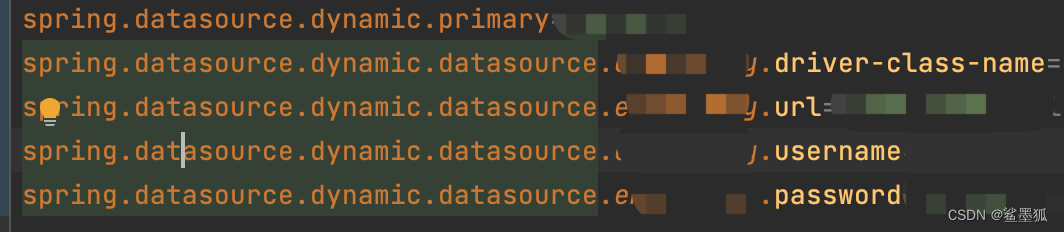
springboot dynamic配置多数据源
pom.xml引入jar包 <dependency><groupId>com.baomidou</groupId><artifactId>dynamic-datasource-spring-boot-starter</artifactId><version>3.5.2</version> </dependency> application配置文件配置如下 需要主要必须配置…...
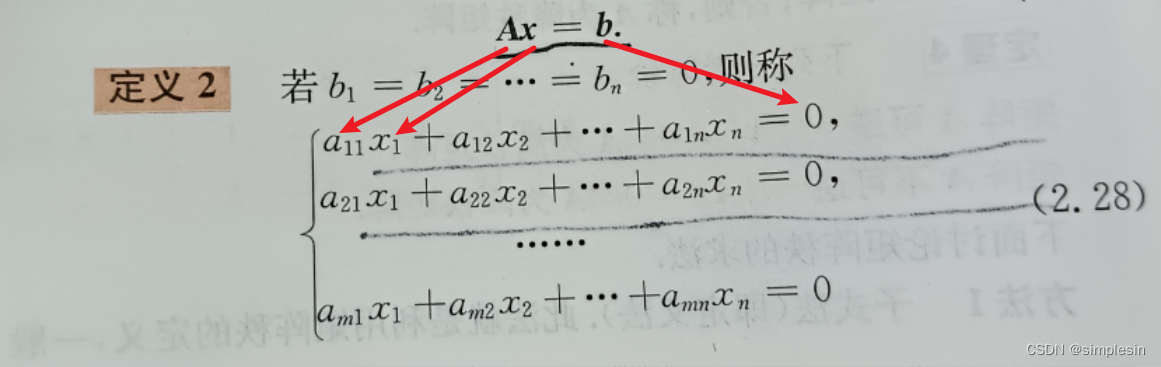
线性代数知识点搜刮
求你别考太细... 目录 异乘变零定理 行列式转置 值不变 重要关系 中间相等,取两头 特征值公式 向量正交 点积为0 拉普拉斯定理 矩阵的秩 特征值和特征向量 |A|特征值的乘积 & tr(A)特征值的和 要记要背 增广矩阵 异乘变零定理 某行(…...

景区智能厕所系统,打造智能化,人性化公共空间
在智慧旅游的大潮中,景区智能厕所系统正逐渐成为提升公共空间智能化、人性化水平的关键载体。作为智慧城市建设的重要组成部分,智能厕所系统不仅解决了传统公厕存在的诸多问题,更通过科技的力量,为游客创造了更加舒适、便捷的如厕…...

Windows中Git的使用(2024最新版)
Windows中Git的使用 获取ssh keys本地绑定邮箱初始化本地仓库添加到本地缓存区提交到本地缓存区切换本地分支为main关联远程分支推送到GitHub查看推送日志 Git 2020年发布了新的默认分支名称"main",取代了"master"作为主分支的名称。操作有了些…...
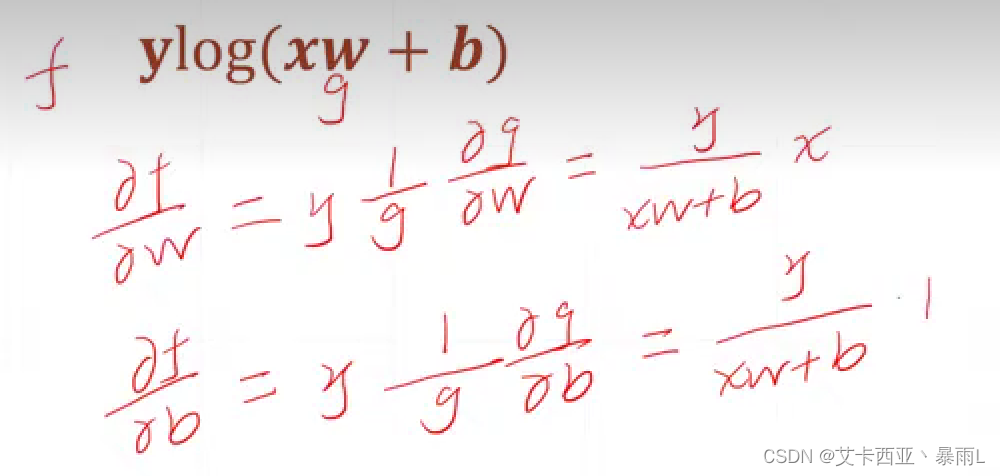
【pytorch12】什么是梯度
说明 导数偏微分梯度 梯度:是一个向量,向量的每一个轴是每一个方向上的偏微分 梯度是有方向也有大小,梯度的方向代表函数在当前点的一个增长的方向,然后这个向量的长度代表了这个点增长的速率 蓝色代表比较小的值,红色…...

南京,协同开展“人工智能+”行动
南京,作为江苏省的省会城市,一直以来都是科技创新和产业发展的高地。近日,南京市政府正式印发了《南京市进一步促进人工智能创新发展行动计划(2024—2026 年)》和《南京市促进人工智能创新发展若干政策措施》的“11”文…...
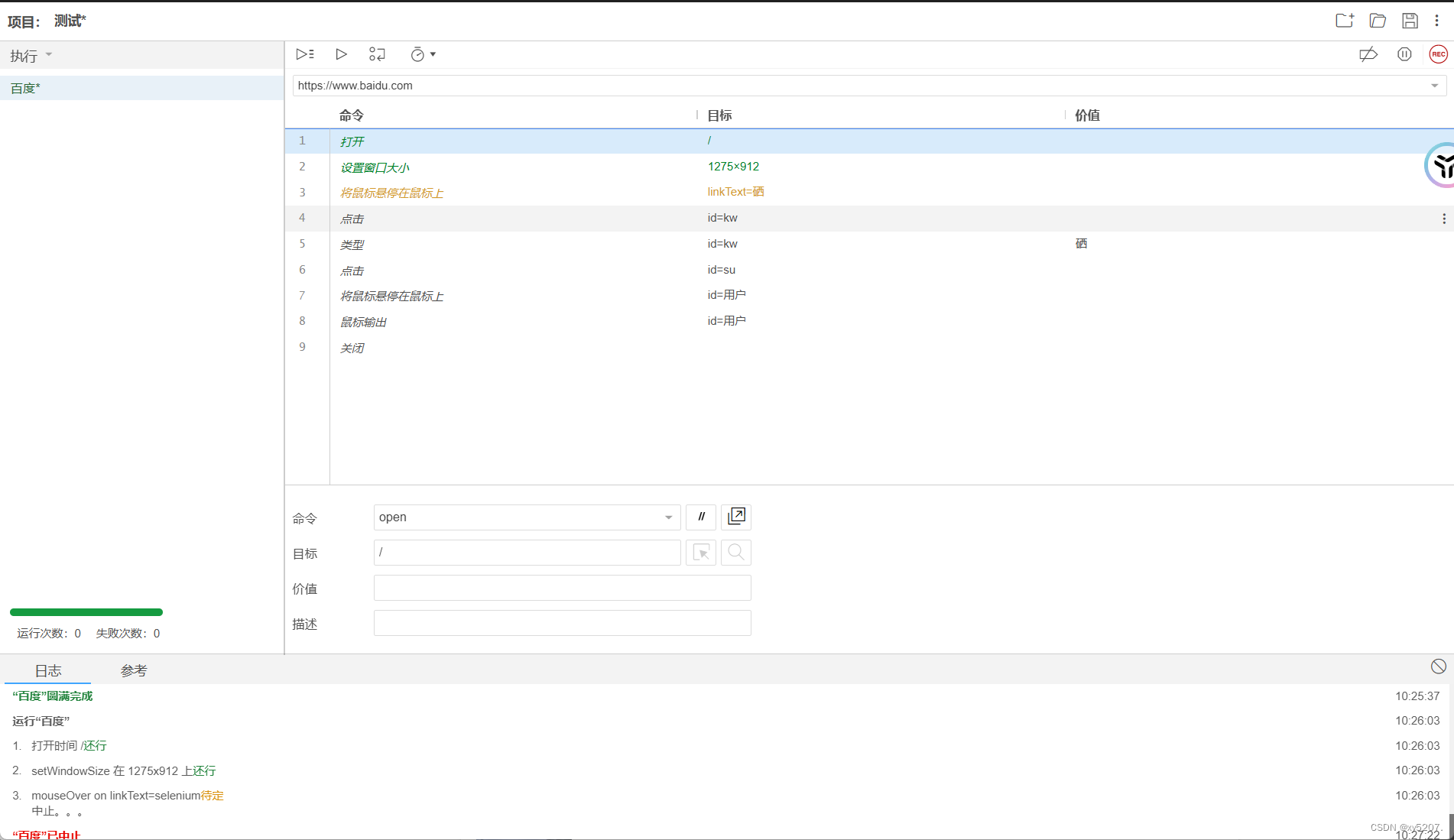
Selenium IDE 的使用指南
Selenium IDE 的使用指南 在自动化测试的领域中,Selenium 是一个广为人知且强大的工具集。而 Selenium IDE 作为其中的一个组件,为测试人员提供了一种便捷且直观的方式来创建和执行自动化测试脚本。 一、Selenium IDE 简介 Selenium IDE 是一个用于录…...

vue配置sql规则
vue配置sql规则 实现效果组件完整代码父组件 前端页面实现动态配置sql条件,将JSON结构给到后端,后端进行sql组装。 这里涉及的分组后端在组装时用括号将这块规则括起来就行,分组的sql连接符(并且/或者)取组里的第一个。…...

面试官:Redis执行lua脚本能保证原子性吗?
核心问题 Redis执行lua脚本是否能确保原子性? 面试经历 面试者在面试中自信回答Redis执行lua脚本能保证原子性,但未能深入解释原因。 原子性概念 原子性:一个事务的所有命令要么全部执行成功,要么全部执行失败。 Redis官方说…...

基于Chrome扩展的浏览器可信事件与网页离线PDF导出
基于Chrome扩展的浏览器可信事件与网页离线PDF导出 Chrome扩展是一种可以在浏览器中添加新功能和修改浏览器行为的软件程序,我们可以基于Manifest规范的API实现对于浏览器和Web页面在一定程度上的修改,例如广告拦截、代理控制等。Chrome DevTools Proto…...
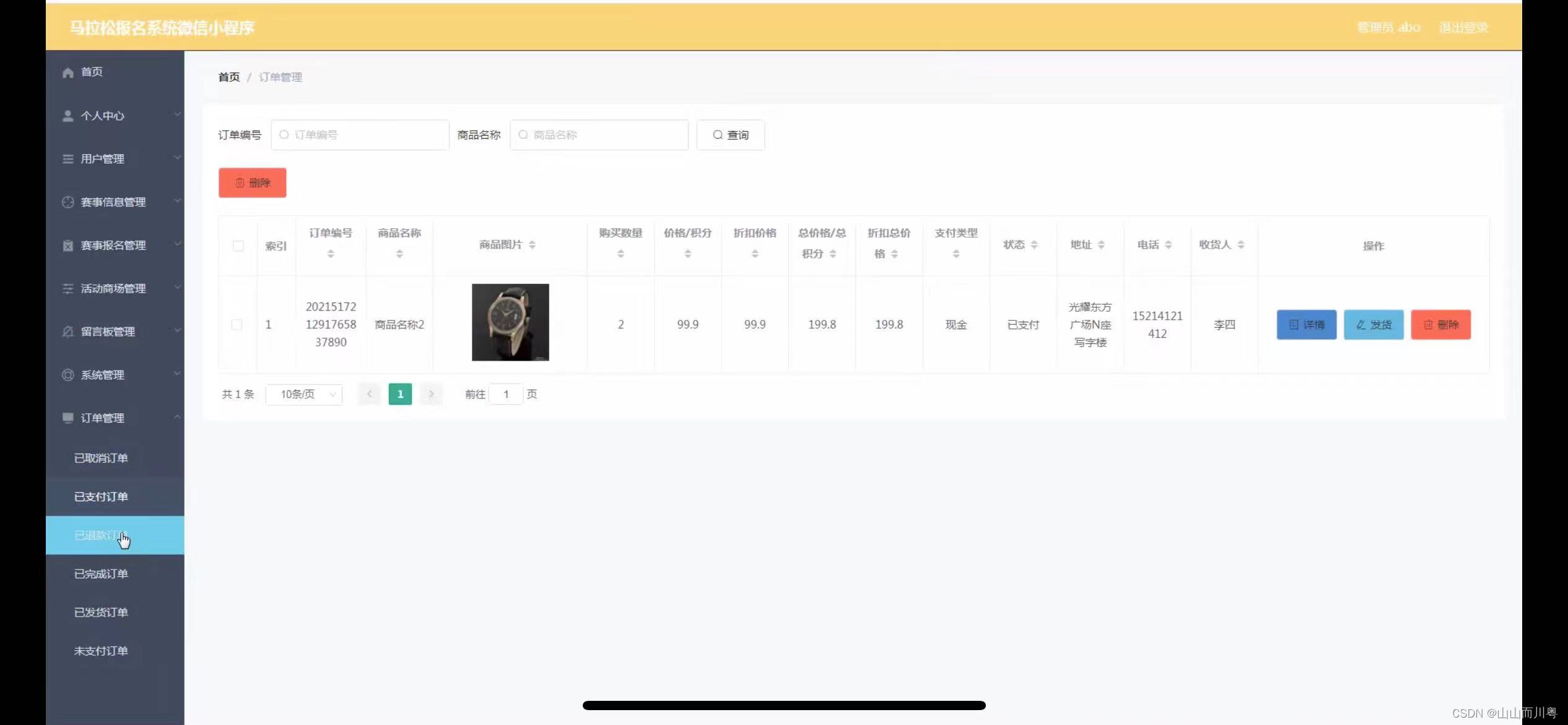
马拉松报名小程序的设计
管理员账户功能包括:系统首页,个人中心,用户管理,赛事信息管理,赛事报名管理,活动商城管理,留言板管理,系统管理 微信端账号功能包括:系统首页,赛事信息&…...
python使用pywebview集成vue3和element-plus开发桌面系统框架
随着web技术越来越成熟,就连QQ的windows客户端都用web技术来开发,所以在未来,web技术来开发windows桌面软件也会越来越多,所以在此发展驱动之下,将最近流程的python与web技术相结合,使用vue3和element-plus…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...
