当前位置：首页 > news >正文

基于布雷格曼偏差校正技术的全变分一维时间序列信号降噪方法（MATLAB R2018A）

news 文章来源：https://blog.csdn.net/weixin_39402231/article/details/140110255 2024/10/5 14:24:21

信号降噪是信号处理的重要步骤之一，目的是提高所获得信号数据的质量，以达到更高的定性和定量分析精度。信号降噪能提升信号处理其他环节的性能和人们对信息识别的准确率，给信号处理工作提供更可靠的保证。信号降噪的难点是降低噪声的同时也会破坏原始信号中一些有效的细节信息，如峰或边缘。在分析信号中，谱峰包含着重要的物理或化学性质。为了降低信号中的噪声，通常需要对信号进行平滑处理，尤其对于导数谱分析方法，信号平滑是必不可少的环节，一旦谱峰被平滑掉，在后续分析过程中很难再恢复，从而影响分析结果。

时间域降噪直接对信号本身进行处理，包括滑动均值法、Savitzky-Golay 方法、正则化方法、中值滤波以及基于偏微分方程的方法等。滑动均值法是用滑动窗口内所有点的平均值替换中心点来实现平滑。Savitzky-Golay 方法是滑动均值法的推广，它通过一个低阶多项式来拟合整个窗口内的数据。作为 Savitzky-Golay 方法的改进，一种基于惩罚最小二乘的正则化方法被提出。中值滤波是一种非线性滤波方法，它是将邻域内所有点按强度排序，然后用中间值代替邻域中心点来实现滤波。邻域窗口的大小和形状对降噪效果有着很大的影响。基于偏微分方程的方法是将降噪过程看作物理学中的热扩散，通过求解热扩散方程得到最终的降噪结果。

变换域降噪方法是将信号从时间域变换到频域，然后处理变换后的系数，最终通过逆变换获得降噪后的信号。长期以来，傅里叶变换是变换域降噪的主要手段，对于平稳信号有着不错的效果，但在实际应用中，大多数信号都是非平稳的，这给傅里叶变换降噪带来了困难。随着小波理论的不断发展，小波方法逐渐被应用于信号降噪领域。Mallat 提出了信号奇异性检测的理论，并利用小波变换模极大值的方法进行信号降噪；Donoho提出了基于非线性小波变换阈值的信号降噪方法。但是，该方法会在信号不连续处产生伪吉布斯现象，于是在阈值法的基础上，一种改进的平移不变量小波降噪方法被提出。此外，多小波与小波包理论的研究也为变换域降噪带来了新的方法。

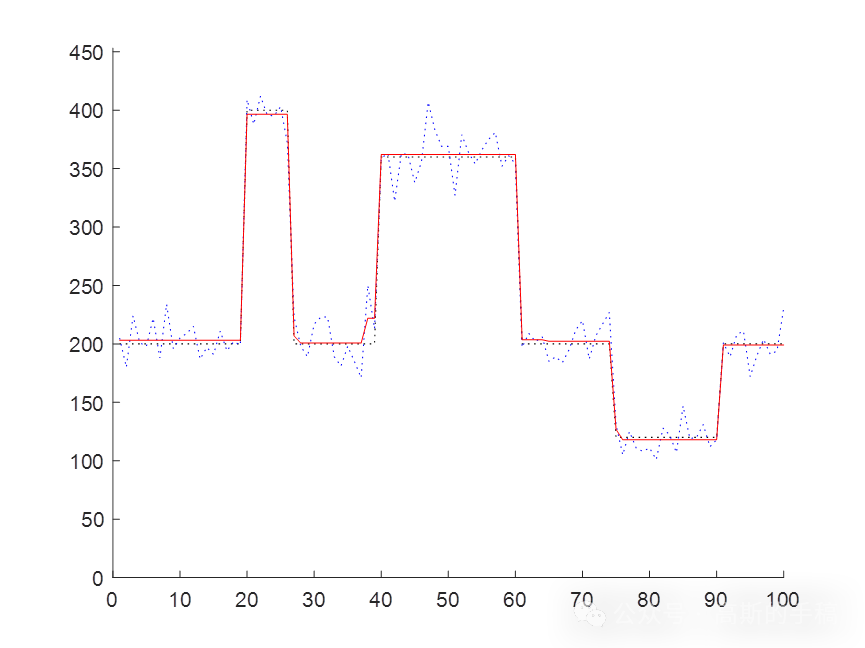
鉴于此，采用基于布雷格曼偏差校正技术的全变分一维时间序列信号降噪方法，运行环境为MATLAB R2018A。


function [u, iter] = denoise_1D(g, mu, delta)
l.
%
% Input:    g       -   noisy 1D signal
%           mu      -   regularization parameter
%           delta   -   noise level. needed for disc. principle stop crit
%                       If noise level is not set, use a variance estimate
% Output:   u       -   solution of the ROF model%% check inputs, potentially assign discrepancy principle threshold
fprintf('Bregman iterative denoising started\n');assert(size(g,1) == 1 || size(g,2) == 1, 'input signal must be 1D')
g = reshape(g,[],1);
N = size(g,1);% if no noise level is set, use variance estimate
if nargin == 2delta = sqrt((N-1)*var(g)); fprintf('no noise level provided, estimating discrepancy principle threshold to sqrt((N-1)*variance).\n');fprintf('Iterate until ||u-f||_2 < %.4f.\n',delta);
elsefprintf('Iterate until ||u-f||_2 < %.4f.\n',delta);
end%% iteration
u = zeros(N,1);
v = u;
k = 0;
fprintf('%5s\t|\t%12s\t|\t%12s\n','k','||u-f||_2','||v||_2');
fprintf([repmat('_',1,45),'\n'])
while norm(u - g) > deltak = k + 1;u = ROF_1D(g + v,mu);     % modified ROFv = v + g - u;                  % update noisefprintf('%5d\t|\t%12.4g\t|\t%12.4g\n',k,norm(u-g),norm(v));
end
end完整代码：https://mbd.pub/o/bread/ZpWXlpdq
擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。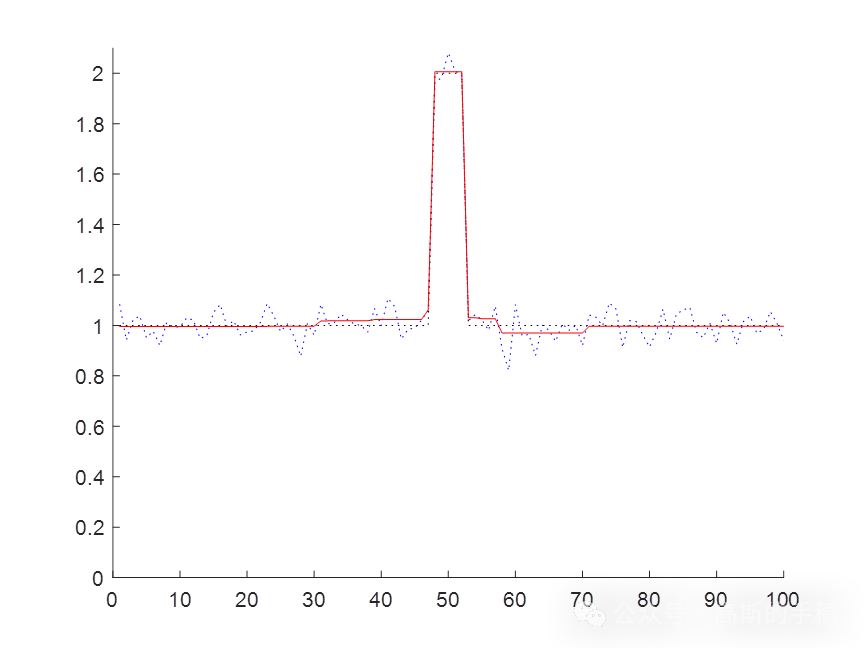

擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。

相关文章：