Finding Global Homophily in Graph Neural Networks When Meeting Heterophily
本文发表于:ICML22
推荐指数: #paper/⭐⭐⭐
问题背景:
异配图的邻接矩阵难以确定,以及异配图的计算复杂度开销大
可行的解决办法:高通滤波+多跳邻居,GPRGNN(pagerank一类,各阶邻居的权重不同,ACM-GCN(高低通滤波,H2GCN(应该复杂度很大) WRGAT,GGCN(signed message) LINKX(MLP+graph)
模型

方法:两个MLP学习X和A,拼接后卷积
H X ( 0 ) = M L P 1 ( X ) , H A ( 0 ) = M L P 2 ( A ) H_X^{(0)}=M\mathrm{LP}_1(X),~H_A^{(0)}=\mathrm{MLP}_2(A) HX(0)=MLP1(X), HA(0)=MLP2(A)
仿照APPNP,再加上初等残差:
H ( 0 ) = ( 1 − α ) H X ( 0 ) + α H A ( 0 ) H^{(0)}=(1-\alpha)H_X^{(0)}+\alpha H_A^{(0)} H(0)=(1−α)HX(0)+αHA(0)
H ( l ) = ( 1 − γ ) Z ( l ) H ( l ) + γ H ( 0 ) + O ( l ) H^{(l)}=(1-\gamma)Z^{(l)}H^{(l)}+\gamma H^{(0)}+O^{(l)} H(l)=(1−γ)Z(l)H(l)+γH(0)+O(l)
我们可以得到下面优化问题:
min Z ( l ) ∥ H ( l ) − ( 1 − γ ) Z ( l ) H ( l ) − γ H ( 0 ) ∥ F 2 + β 1 ∥ Z ( l ) ∥ F 2 + β 2 ∥ Z ( l ) − ∑ k = 1 K λ k A ^ k ∥ F 2 \min_{Z^{(l)}}\|H^{(l)}-(1-\gamma)Z^{(l)}H^{(l)}-\gamma H^{(0)}\|_{F}^{2}+\beta_{1}\|Z^{(l)}\|_{F}^{2}+\beta_{2}\|Z^{(l)}-\sum_{k=1}^{K}\lambda_{k}\hat{A}^{k}\|_{F}^{2} Z(l)min∥H(l)−(1−γ)Z(l)H(l)−γH(0)∥F2+β1∥Z(l)∥F2+β2∥Z(l)−k=1∑KλkA^k∥F2
第一项是优化问题,第二项是F范数,第三项是逼近Z与多跳邻居
可得Z:
Z ( l ) ∗ = [ ( 1 − γ ) H ( l ) ( H ( l ) ) T + β 2 ∑ k = 1 K λ k A ^ k − γ ( 1 − γ ) H ( 0 ) ( H ( l ) ) T ] [ ( 1 − γ ) 2 H ( l ) ( H ( l ) ) T + ( β 1 + β 2 ) I n ] − 1 \begin{aligned} Z^{(l)*}& =\left[(1-\gamma)H^{(l)}(H^{(l)})^T+\beta_2\sum_{k=1}^K\lambda_k\hat{A}^k-\gamma(1-\gamma)H^{(0)}(H^{(l)})^T\right] \\ &\left[\left(1-\gamma\right)^2H^{(l)}(H^{(l)})^T+(\beta_1+\beta_2)I_n\right]^{-1} \end{aligned} Z(l)∗=[(1−γ)H(l)(H(l))T+β2k=1∑KλkA^k−γ(1−γ)H(0)(H(l))T][(1−γ)2H(l)(H(l))T+(β1+β2)In]−1
计算加速
H ( l + 1 ) = ( 1 − γ ) Z ( l ) ∗ H ( l ) + γ H ( 0 ) . H^{(l+1)}=(1-\gamma)Z^{(l)*}H^{(l)}+\gamma H^{(0)}. H(l+1)=(1−γ)Z(l)∗H(l)+γH(0).
H ( l + 1 ) = ( 1 − γ ) H ( l ) ( H ( l ) ) T Q ( l + 1 ) + β 2 ∑ k = 1 K λ k A ^ k Q ( l + 1 ) − γ ( 1 − γ ) H ( 0 ) ( H ( l ) ) T Q ( l + 1 ) + γ H ( 0 ) \begin{gathered} H^{(l+1)}= (1-\gamma)H^{(l)}(H^{(l)})^TQ^{(l+1)}+\beta_2\sum_{k=1}^K\lambda_k\hat{A}^kQ^{(l+1)} \\ -\gamma(1-\gamma)H^{(0)}(H^{(l)})^TQ^{(l+1)}+\gamma H^{(0)} \end{gathered} H(l+1)=(1−γ)H(l)(H(l))TQ(l+1)+β2k=1∑KλkA^kQ(l+1)−γ(1−γ)H(0)(H(l))TQ(l+1)+γH(0)
其中, Q ( l + 1 ) = 1 − γ β 1 + β 2 H ( l ) − 1 − γ ( β 1 + β 2 ) 2 H ( l ) . [ 1 ( 1 − γ ) 2 I c + 1 β 1 + β 2 ( H ( l ) ) T H ( l ) ] − 1 ( H ( l ) ) T H ( l ) \begin{aligned} Q^{(l+1)}=& \frac{1-\gamma}{\beta_1+\beta_2}H^{(l)}-\frac{1-\gamma}{(\beta_1+\beta_2)^2}H^{(l)}. \\ &\left[\frac1{(1-\gamma)^2}I_c+\frac1{\beta_1+\beta_2}(H^{(l)})^TH^{(l)}\right]^{-1}(H^{(l)})^TH^{(l)} \end{aligned} Q(l+1)=β1+β21−γH(l)−(β1+β2)21−γH(l).[(1−γ)21Ic+β1+β21(H(l))TH(l)]−1(H(l))TH(l)
Group Effective
Definition 4. 1. ( Grouping effect ( Li et al. , 2020) ) . Given \textbf{Definition 4. 1. }( \textbf{Grouping effect ( Li et al. , 2020) ) . Given} Definition 4. 1. (Grouping effect ( Li et al. , 2020) ) . Given,a set of nodes V = { v i } i = 1 n \mathcal{V}=\{v_i\}_{i=1}^n V={vi}i=1n, let v i → v j v_i\to v_j vi→vj denote the condi-tion that ( 1 ) ∥ x i − x j ∥ 2 → 0 (1)\left\|x_i-x_j\right\|_2\to0 (1)∥xi−xj∥2→0 and ( 2 ) ∥ a ^ i k − a ^ j k ∥ 2 → 0 ( 2) \left \| \hat{a} _i^k- \hat{a} _j^k\right \| _2\to 0 (2) a^ik−a^jk 2→0, ∀ k ∈ \forall k\in ∀k∈ [ 1 , K ] . [1,K]. [1,K]. A matrix Z Z Z is said to have grouping effect if
v i → v j ⇒ ∣ Z i p − Z j p ∣ → 0 , ∀ 1 ≤ p ≤ n . v_i\to v_j\Rightarrow|Z_{ip}-Z_{jp}|\to0,\forall1\leq p\leq n. vi→vj⇒∣Zip−Zjp∣→0,∀1≤p≤n.
对于任意两个节点vi和vj,无论它们在图中有多远,如果它们共享相似的特征向量和局部结构,我们都可以得出结论:(1),它们将被给予相似的系数向量;(2),它们将在描述其他节点时扮演相似的角色;而(3),它们将得到相似的表示向量。另一方面,在具有异质性的图中,相邻的节点更有可能出现不同的情况,因此它们会得到不同的嵌入。此外,对于特征相似度较低的两个节点,如果它们具有较高的结构相似性,则可以通过局部图结构的正则化项来增强其表征
GloGNN++
之前的这个H矩阵是 纵向的 attention,即 节点和 邻居之间的。 这里提出 横向的 attention,就是自身节点特征的重要性不同,采用常规的方法,增加一个对角矩阵作为每一维特征的attention
讨论
1.GAT中的权重是自动学习的,缺乏可解释性,但我们的模型中的Z(l)是来自一个精心设计良好的优化问题,并且有一个封闭的解
2.其次,GAT中的注意权值总是非负值,而我们的方法中的Z(l)允许有符号值。因此,GAT只使用低通卷积滤波器,而我们的方法同时结合了低通和高通滤波器。
3.对于每个节点,GAT对图中所有节点执行的邻域聚合计算代价昂贵,具有二次时间复杂度w.r.t.节点数。然而,我们的方法加速了聚合,并推导出了一个线性的时间复杂度
相关文章:

Finding Global Homophily in Graph Neural Networks When Meeting Heterophily
本文发表于:ICML22 推荐指数: #paper/⭐⭐⭐ 问题背景: 异配图的邻接矩阵难以确定,以及异配图的计算复杂度开销大 可行的解决办法:高通滤波多跳邻居,GPRGNN(pagerank一类,各阶邻居的权重不同,ACM-GCN(高低通滤波,H2GCN(应该复杂度很大&…...

DisFormer:提高视觉动态预测的准确性和泛化能力
最新的研究进展已经显示出目标中心的表示方法在视觉动态预测任务中可以显著提升预测精度,并且增加模型的可解释性。这种表示方法通过将视觉场景分解为独立的对象,有助于模型更好地理解和预测场景中的变化。 尽管在静态图像的解耦表示学习方面已经取得了一…...
)
Android SurfaceFlinger——Surface和Layer介绍(十九)
按照前面系统开机动画的流程继续分析,在获取到显示屏信息后,下一步就是开始创建 Surface和设置 Layer 层级,这里就出现了两个新的概念——Surface 和 Layer。 一、基本概念 1、Surface介绍 在 Android 系统中,Surface 是一个非常核心的概念,它是用于显示图像的生产者-消…...

C++基础(七):类和对象(中-2)
上一篇博客学的默认成员函数是类和对象的最重要的内容,相信大家已经掌握了吧,这一篇博客接着继续剩下的内容,加油! 目录 一、const成员(理解) 1.0 引入 1.1 概念 1.2 总结 1.2.1 对象调用成员函数 …...

对秒杀的思考
一、秒杀的目的 特价商品,数量有限,先到先得,售完为止 二、优惠券的秒杀 和特价商品的秒杀是一样的,只不过秒杀的商品是优惠券 三、秒杀的需求 秒杀前:提前将秒杀商品,存放到Redis秒杀中:使…...
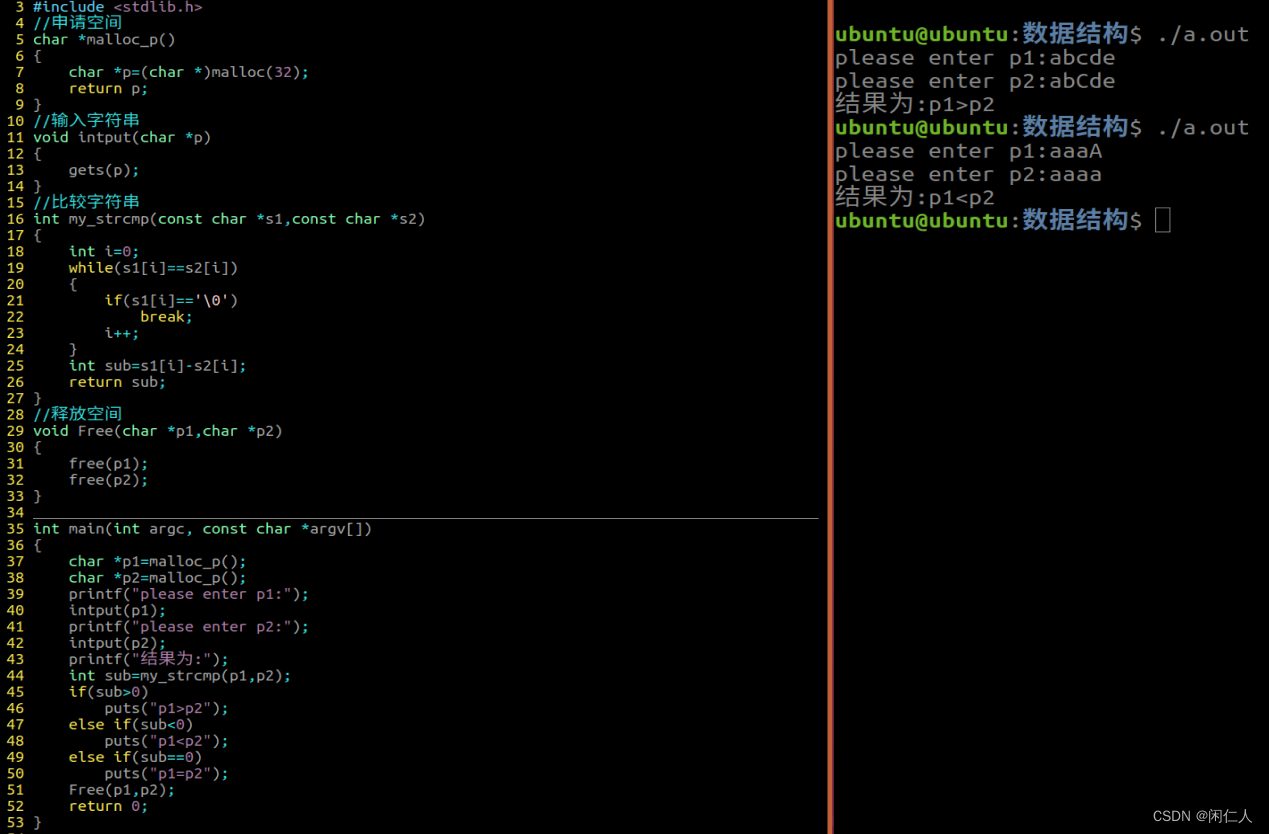
数据结构预科
在堆区申请两个长度为32的空间,实现两个字符串的比较【非库函数实现】 要求: 1> 定义函数,在对区申请空间,两个申请,主函数需要调用2次 2> 定义函数,实现字符串的输入,void input(char …...

想做亚马逊测评技术需要解决哪些问题,有哪些收益?
现在真正有亚马逊测评技术的人赚的盆满钵满,有些人看到别人赚取就自己盲目去做,买完了账号和设备就感觉自己懂了,却不知里面的水深着,花了钱却没有掌握真正的技术,号莫名其妙就封完了,而每一次大风控注定要…...

1117 数字之王
solution 判断现有数字是否全为个位数 全为个位数,找出出现次数最多的数字,并首行输出最多出现次数,第二行输出所有出现该次数的数值不全为个位数 若当前位数值为0,无需处理若当前位数值非0,则每位立方相乘࿰…...

关于ORACLE单例数据库中的logfile的切换、删除以及添加
一、有关logfile的状态解释 UNUSED: 尚未记录change的空白group(一般会出现在loggroup刚刚被添加,或者刚刚使用了reset logs打开数据库,或者使用clear logfile后) CURRENT: 当前正在被LGWR使用的gro…...

Linux高并发服务器开发(十三)Web服务器开发
文章目录 1 使用的知识点2 http请求get 和 post的区别 3 整体功能介绍4 基于epoll的web服务器开发流程5 服务器代码6 libevent版本的本地web服务器 1 使用的知识点 2 http请求 get 和 post的区别 http协议请求报文格式: 1 请求行 GET /test.txt HTTP/1.1 2 请求行 健值对 3 空…...

人工智能系列-NumPy(二)
🌈个人主页:羽晨同学 💫个人格言:“成为自己未来的主人~” 链接数组 anp.array([[1,2],[3,4]]) print(第一个数组:) print(a) print(\n) bnp.array([[5,6],[7,8]]) print(第二个数组:) print(b) print(\n) print…...

[单master节点k8s部署]19.监控系统构建(四)kube-state-metrics
kube-state-metrics 是一个Kubernetes的附加组件,它通过监听 Kubernetes API 服务器来收集和生成关于 Kubernetes 对象(如部署、节点和Pod等)的状态的指标。这些指标可供 Prometheus 进行抓取和存储,从而使你能够监控和分析Kubern…...

字符串函数5-9题(30 天 Pandas 挑战)
字符串函数 1. 相关知识点1.5 字符串的长度条件判断1.6 apply映射操作1.7 python大小写转换1.8 正则表达式匹配2.9 包含字符串查询 2. 题目2.5 无效的推文2.6 计算特殊奖金2.7 修复表中的名字2.8 查找拥有有效邮箱的用户2.9 患某种疾病的患者 1. 相关知识点 1.5 字符串的长度条…...

【C语言题目】34.猜凶手
文章目录 作业标题作业内容2.解题思路3.具体代码 作业标题 猜凶手 作业内容 日本某地发生了一件谋杀案,警察通过排查确定杀人凶手必为4个嫌疑犯的一个。 以下为4个嫌疑犯的供词: A说:不是我。 B说:是C。 C说:是D。 D说ÿ…...

C++ 多进程多线程间通信
目录 一、进程间通信 1、管道(Pipe) 2、消息队列(Message Queue) 3、共享内存(Shared Memory) 4、信号量(Semaphore) 5、套接字(Socket) 6、信号&…...

怎么做防御系统IPS
入侵防御系统(IPS)是入侵检测系统(IDS)的增强版本,它不仅检测网络流量中的恶意活动,还能自动采取措施阻止这些活动。实现IPS的主要工具包括Snort和Suricata。以下是使用Snort和Suricata来实现IPS的详细步骤…...

达梦数据库的系统视图v$auditrecords
达梦数据库的系统视图v$auditrecords 在达梦数据库(DM Database)中,V$AUDITRECORDS 是专门用来存储和查询数据库审计记录的重要系统视图。这个视图提供了对所有审计事件的访问权限,包括操作类型、操作用户、时间戳、目标对象等信…...

Spring Boot与MyBatis-Plus:代码逆向生成指南
在Spring Boot项目中使用MyBatis-Plus进行代码逆向生成,可以通过MyBatis-Plus提供的代码生成器来快速生成实体类、Mapper接口、Service接口及其实现类等。以下是一个简单的示例步骤: 代码逆向生成 1.添加依赖: 在pom.xml文件中添加MyBati…...
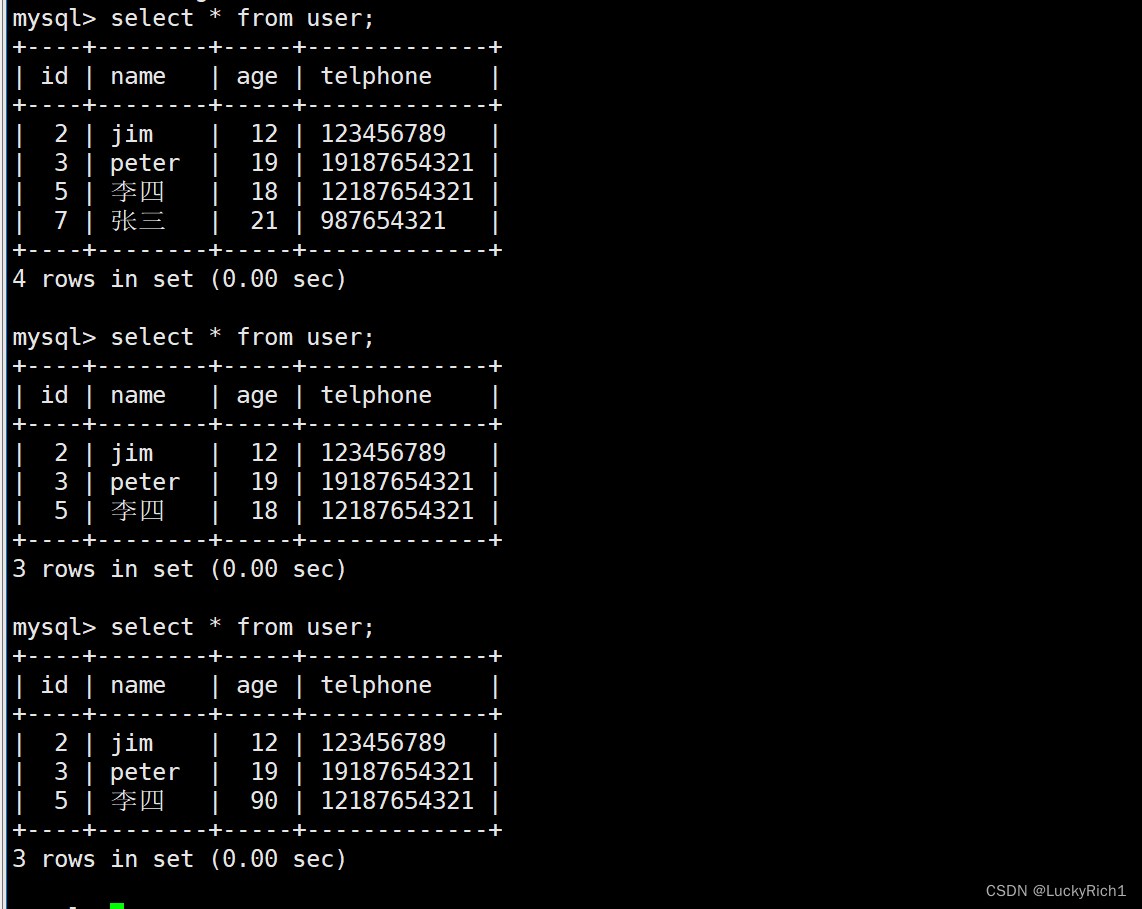
【MySQL】mysql访问
mysql访问 1.引入MySQL 客户端库2.C/C 进行增删改3.查询的处理细节4.图形化界面访问数据库4.1下载MYSQL Workbench4.2MYSQL Workbench远程连接数据库 点赞👍👍收藏🌟🌟关注💖💖 你的支持是对我最大的鼓励&a…...
(1)Jupyter Notebook 下载及安装
目录 1. Jupyter Notebook是什么?2. Jupyter Notebook特征3. 组成部分3.1 网页应用3.2 文档 4. 适用场景5. 利用Google Colab安装Jupyter Notebook3.1 什么是 Colab?3.2 访问 Google Colab3.3 新建笔记本 1. Jupyter Notebook是什么? 百度百科…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
