Java求自然常数e的近似值(课堂实例1)
❤❤引言🎃🎃
❤点关注编程梦想家(大学生版)-CSDN博客不迷路~~~~~~❤
自然常数 𝑒e 是数学中一个非常重要的常数,约等于 2.71828,它在自然对数、复合利息计算等领域有着广泛的应用。本文将介绍如何使用Java编程语言来计算自然常数 𝑒e 的近似值。
一、自然常数 𝑒e 的定义
自然常数 𝑒e 可以通过无限级数求和来定义:
𝑒=∑𝑛=0∞1𝑛!=1+11!+12!+13!+⋯e=∑n=0∞n!1=1+1!1+2!1+3!1+⋯
二、算法实现
在Java中,我们可以使用一个循环来计算上述级数的每一项,并累加到结果中。为了提高计算效率,我们可以在计算 𝑛!n! 时使用一个累积变量。
1.Java代码实现
public class Calculate {public static void main(String[] args) {int precision = 10; // 精度,即计算前10项double e = calculateE(precision);System.out.printf("自然常数 e 的近似值为: %.5f%n", e);}public static double calculateE(int precision) {double e = 1.0; // 初始化e的值double factorial = 1.0; // 用于累积阶乘的值for (int i = 1; i <= precision; i++) {factorial *= i; // 计算阶乘e += 1.0 / factorial; // 累加级数项}return e;}
}2.代码解释
main方法中,我们设置了计算的精度,即计算前precision项。calculateE方法接受一个整数参数precision,表示计算级数的项数。- 我们使用一个
for循环来计算每一项,并累加到变量e中。factorial变量用于累积阶乘的值,避免了重复计算。- 使用
System.out.printf来格式化输出结果。
三、结果分析
随着 precision 值的增加,计算得到的 𝑒e 的近似值将更加接近真实值。然而,由于计算机的浮点数精度限制,当 precision 非常大时,结果可能会受到精度误差的影响。
四、结语
本文介绍了自然常数 𝑒e 的定义和使用Java计算其近似值的方法。通过调整计算精度,可以得到不同精度的 𝑒e 值。希望本文能够帮助你理解自然常数 𝑒e 以及如何在Java中实现相关计算。
五、参考资料
自然常数_百度百科 (baidu.com)
相关文章:
)
Java求自然常数e的近似值(课堂实例1)
❤❤引言🎃🎃 ❤点关注编程梦想家(大学生版)-CSDN博客不迷路~~~~~~❤ 自然常数 𝑒e 是数学中一个非常重要的常数,约等于 2.71828,它在自然对数、复合利息计算等领域有着广泛的应用。本文将介绍如…...

简过网:什么是咨询工程师?我不允许还有人不知道!
咨询工程师真的有必要考吗?近期小编收到很多关于咨询工程师的的问题,今天,小编给大家整理汇总了一下关于咨询工程师的相关问题,希望能够帮助到大家! 一、什么是咨询工程师? 咨询工程师是从事工程咨…...

数据泄露时代的安全之道:访问认证的重要性
引言 想象一下:你一觉醒来,收到一条通知——你的公司遭遇了数据泄露。你感到恐惧,因为这意味着客户数据被曝光,公司声誉受损,还有巨额罚款在等着你。在当今的数字化环境中,这种情况太常见了。全球各地的组…...

XLSX + LuckySheet + LuckyExcel + Web Worker实现前端的excel预览
文章目录 功能简介简单代码实现web worker 版本效果参考 功能简介 通过LuckyExcel的transformExcelToLucky方法, 我们可以把一个文件直接转成LuckySheet需要的json字符串, 之后我们就可以用LuckySheet预览excelLuckyExcel只能解析xlsx格式的excel文件&a…...
)
Java版本迭代的过程(Java面经)
Java 5: 泛型与注解 泛型:使得Web应用可以编写更加类型安全的代码,特别是在处理各种数据结构时,如集合框架的使用。注解:极大地简化了配置管理,Spring框架的崛起得益于Java 5的注解支持,使得依赖注入和AOP…...
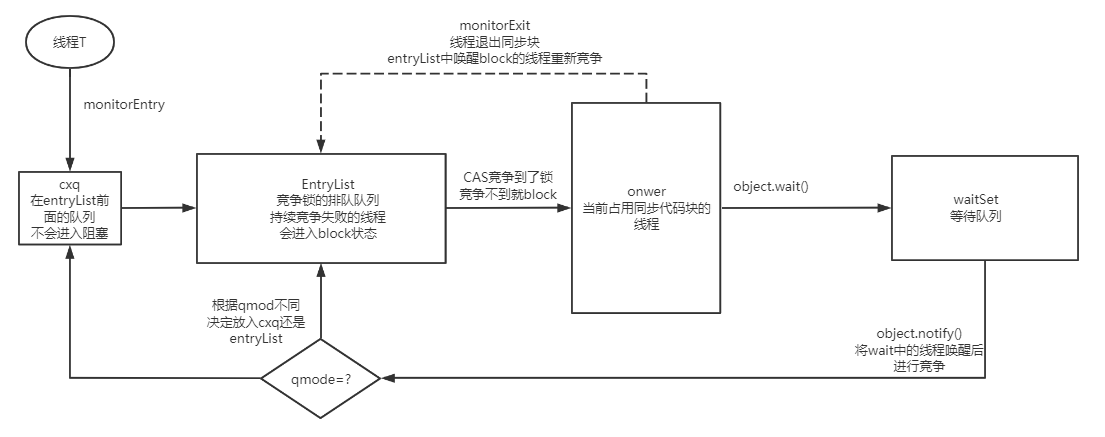
深入了解java锁升级可以应对各种疑难问题
对于java锁升级,很多人都停留在比较浅层的表面理解,一定程度下也许够用,但如果学习其中的细节,我们更好地理解多线程并发时各种疑难问题的应对方式! 因此我将锁升级过程中可能涉及的大部分细节或者疑问都整合成了一篇…...

C++初学者指南-4.诊断---基础:警告和测试
C初学者指南-4.诊断—基础知识:警告和测试 文章目录 C初学者指南-4.诊断---基础知识:警告和测试1. 术语和技术记住:使用专用类型! 2.编译器警告Gcc/CLang 编译器选项MS Visual Studio 编译器选项 3.断言运行时断言静态断言&#x…...

docker使用镜像jms_all部署jumpserver
创建容器需要挂载出来的服务器对应目录 mkdir -p /data/redis/data mkdir -p /opt/mysql/{data,conf,logs}docker安装redis docker run -d -it --name redis -p 6379:6379 -v /data/redis/data:/data --restart=always...

在Java项目中集成单元测试与覆盖率工具
在Java项目中集成单元测试与覆盖率工具 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 单元测试是软件开发中至关重要的一环,它用于验证代码在独立…...

CTF实战:从入门到提升
CTF实战:从入门到提升 🚀前言 没有网络安全就没有国家安全,网络安全不仅关系到国家整体信息安全,也关系到民生安全。近年来,随着全国各行各业信息化的发展,网络与信息安全得到了进一步重视,越…...

Spring Boot集成olingo快速入门demo
1.什么是olingo? Apache Olingo 是个 Java 库,用来实现 Open Data Protocol (OData)。 Apache Olingo 包括服务客户端和 OData 服务器方面。 Open Data Protocol (开放数据协议,OData) 是用来查询和更新数据的一种W…...
)
GPT对话代码库——HAL库下 USART 的配置及问题(STM32G431CBT6)
目录 1,问: 1,答: 示例代码 正确的HAL库初始化方式 自定义初始化方式(不推荐) 总结 2,问: 2,答: 代码详细解释 初始部分 主初始化部分 初始化调用…...
——ProgressiveMediaPeriod)
ExoPlayer架构详解与源码分析(14)——ProgressiveMediaPeriod
系列文章目录 ExoPlayer架构详解与源码分析(1)——前言 ExoPlayer架构详解与源码分析(2)——Player ExoPlayer架构详解与源码分析(3)——Timeline ExoPlayer架构详解与源码分析(4)—…...

docker部署kafka(单节点) + Springboot集成kafka
环境: 操作系统:win10 Docker:Docker Desktop 4.21.1 (114176)、Docker Engine v24.0.2 SpringBoot:2.7.15 步骤1:创建网络: docker network create --subnet172.18.0.0/16 net-kafka 步骤2:安…...

一.1.(3)半导体二极管基本电路的分析方法及常见应用电路
1.二极管基本电路的分析方法 先标正负极,再看是否理想二极管 将二极管视为断路,求两端电压 两端电压均大于导通电压,压差大的先导通(由于电源不是完全的阶跃,而是有一个电压爬升的过程) 2.常见应用电路 1.求…...

银河麒麟V10 SP1 审计工具 auditd更新
前言 银河麒麟V10 SP1 审计工具 auditd 引发的内存占用过高, 内存使用率一直在 60% 以上, 内存一直不释放 排查 可以使用ps或者top查看系统进程使用情况 ps -aux|sort -k4nr|head -n 5 发现银河麒麟审计工具 auditd 一直占用内存不释放 解决 办法一…...
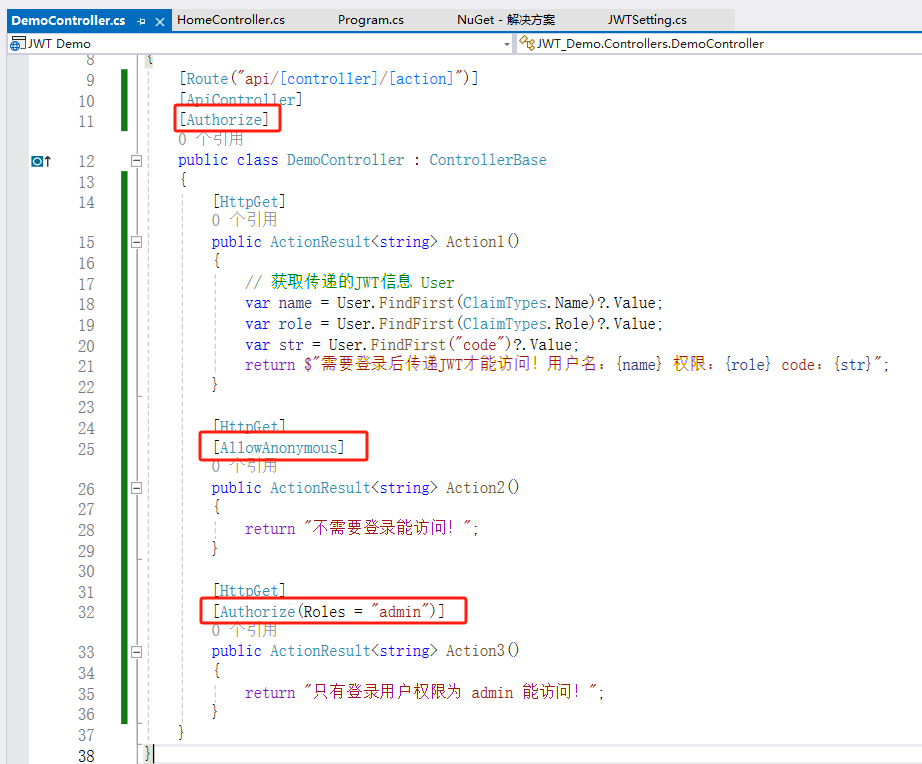
JWT(Json Web Token)在.NET Core中的使用
登录成功时生成JWT字符串目录 JWT是什么? JWT的优点: JWT在.NET Core 中的使用 JWT是什么? JWT把登录信息(也称作令牌)保存在客户端为了防止客户端的数据造假,保存在客户端的令牌经过了签名处理…...

《QT从基础到进阶·四十三》QPlugin插件多线程问题和只有插件dll没有头文件和lib文件时调用插件中的方法
1、插件和多线程问题: 创建插件对象不能放到多线程执行,不然报错:ASSERT failure in QWidget: "Widgets must be created in the GUlthread. //不能放在多线程执行 QPluginLoader pluginLoader(pluginsDir.absoluteFilePath(fileName))…...
)
Android SurfaceFlinger——屏幕状态初始化(二十二)
对于开机启动动画前期准备的相关步骤,我们已经分析了前 5 个,对于第 6 步调用 eglGetDisplay() 函数对 OpenGL ES 初始化并获取默认屏幕,我们在介绍 OpenGL ES 的时候也进行了详细的分析,下一步我们我们来分析对屏幕的状态进行初始化。 1)getInternalDisplayToken:获取显…...

3101. 交替子数组计数 Medium
给你一个 二进制数组 nums 。 如果一个 子数组 中 不存在 两个 相邻 元素的值 相同 的情况,我们称这样的子数组为 交替子数组 。 返回数组 nums 中交替子数组的数量。 示例 1: 输入: nums [0,1,1,1] 输出: 5 解释&…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
