算法系列--分治排序|再谈快速排序|快速排序的优化|快速选择算法

前言:本文就前期学习快速排序算法的一些疑惑点进行详细解答,并且给出基础快速排序算法的优化版本

一.再谈快速排序

快速排序算法的核心是分治思想,分治策略分为以下三步:

1. 分解:将原问题分解为若干相似,规模较小的子问题
2. 解决:如果子问题规模较小,直接解决;否则递归解决子问题
3. 合并:原问题的解等于若干子问题解的合并

应用到快速排序算法:

1. 分解:快速排序算法要实现的是对整个数组进行排序,但是规模较大,要想办法减少规模;他的解决策略是"选择一个基准元素,将数组划分为两部分,左边都是小于基准元素,右边都是大于基准元素",不断的重复上述过程,就能完成对整个数组的排序.对整个数组完成一次这样的操作后,再对左右两个区间分别执行上述过程
2. 递归地对两个子数组进行快速排序，直到每个子数组的长度为0或1，此时数组已经有序。
3. 由于在递归过程中子数组已经被分别排序，因此不需要再进行额外的合并步骤。

二.代码实现和细节讲解

快速排序的关键代码在于如何根据基准元素划分数组区间(parttion),分解的方法有很多,这里只提供一种方法挖坑法
代码:

class Solution {public int[] sortArray(int[] nums) {quick(nums, 0, nums.length - 1);return nums;}private void quick(int[] arr, int start, int end) {if(start >= end) return;// 递归结束条件int pivot = parttion(arr, start, end);// 递归解决子问题quick(arr, start, pivot - 1);quick(arr, pivot + 1, end);}// 挖坑法进行分解private int parttion(int[] arr, int left, int right) {int key = arr[left];while(left < right) {while(left < right && arr[right] >= key) right--;arr[left] = arr[right];while(left < right && arr[left] <= key) ++left;arr[right] = arr[left];}arr[left] = key;return left;}}

---

细节解答:
1.为什么start>=end是递归结束条件?

不断的分解子问题,最终子问题的规模大小是1,即只有一个元素,此时无需继续进行分解,start和end指针同时指向该元素

2.为什么要right先走?而不是left先走?

具体谁先走取决于基准元素的位置,在上述代码中,基准元素(key)是最左边的元素,如果先移动left,left先遇到一个比基准元素大的元素,此时执行arr[right] = arr[left],由于没有保存arr[right],这个元素就会丢失
如果先走right,right先遇到一个比基准元素小的元素,此时执行arr[left]=arr[right],因为此时left并没有移动,还是pivot,但是pivot已经被我们使用key进行保存了

3.为什么是arr[right]>=key?>不行吗

大于等于主要是为了处理重复元素问题
例如有数组[6,6,6,6,6]如果是>,right指针不会发生移动,left指针也不会发生移动,此时陷于死循环

4.为什么叫做挖坑法

当r指针遇到第一个<pivot的元素后停止,执行arr[r] = arr[l],此时l位置就空白出来,形成了一个坑

---

三.快速排序的优化

主要有两个优化方向:

1. 基准值pivot的选取,可以证明的是当随机选取基准值时,快速排序的时间复杂度趋近于O(N*logN),即最好的时间复杂度
2. 重复元素的处理:如果区间内部有大量的重复元素,上述版本的快速排序算法会对相同的元素重复执行多次;为了减少冗余的操作,使用数组分三块的思想解决,同时如果遇到特殊的测试用例(顺序数组或逆序数组)时间复杂度会退化到O(N^2)

先根据一道题目(颜色分类)了解什么是数组分三块
分析

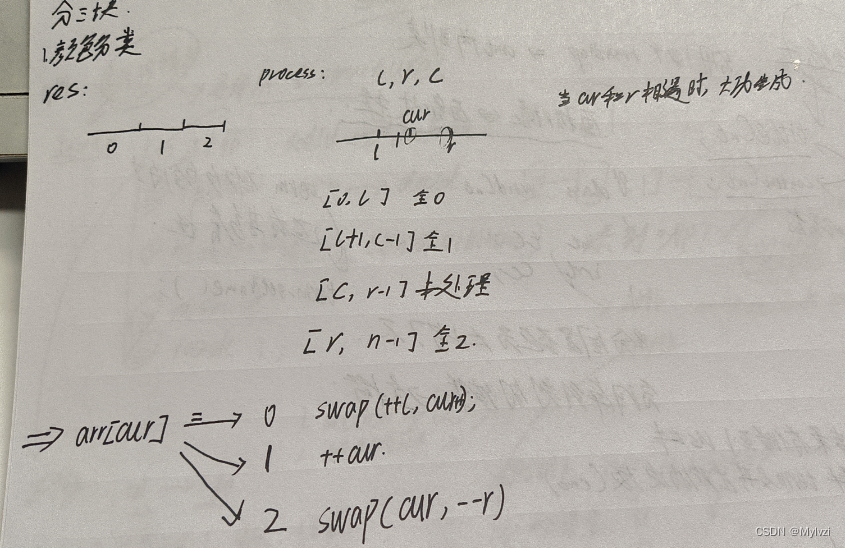
代码:

class Solution {public void sortColors(int[] nums) {// 分治 --// 1.定义三指针int i = 0;// 遍历整个数组int l = -1, r = nums.length;while(i < r) {if(nums[i] == 0) swap(nums,++l,i++);else if(nums[i] == 1) i++;else swap(nums,--r,i);}return;}private void swap(int[] nums,int x,int y) {int tmp = nums[x]; nums[x] = nums[y]; nums[y] = tmp;}
}

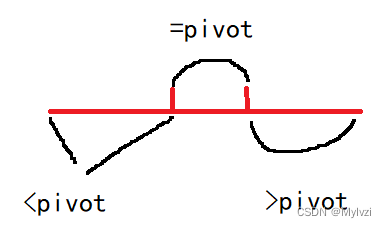
• 注意l,r的起始位置,第一个元素和最后一个元素在开始的时候属于未处理状态,所以`l,r不能指向这两个元素,必须在区间之外
• 所谓的数组分三块,就是使用三个指针去分别维护四个区间,其中的一个区间是未处理区间,随着cur指针的不断移动,所有的区间都被处理,最终也就只有三个区间

将上述思路应用于快速排序的parttion中,最终的结果就是划分为三个区间

代码实现:

class Solution {// 快速排序优化版// 分解--解决--合并public int[] sortArray(int[] nums) {qsort(nums, 0, nums.length - 1);return nums;}private void qsort(int[] nums, int start, int end) {if(start >= end) return;// 递归结束条件// 分解int pivot = nums[start];int l = start - 1, r = end + 1, i = start;while(i < r) {int cur = nums[i];if(cur < pivot) swap(nums, ++l, i++);else if(cur == pivot) ++i;else swap(nums, --r, i);}// [start, l]  [l+1, r-1]  [r, end]// 递归解决qsort(nums, start, l);qsort(nums, r, end);}private void swap(int[] nums,int i, int j) {int tmp = nums[i];  nums[i] = nums[j]; nums[j] = tmp;}
}

2.随机选取基准值
采用随机数的方式随机选取基准值

        int pivot = nums[start + new Random().nextInt(end - start + 1)];//               起始位置      随机产生的偏移量

完整的改进代码:

class Solution {// 快速排序优化版// 分解--解决--合并public int[] sortArray(int[] nums) {qsort(nums, 0, nums.length - 1);return nums;}private void qsort(int[] nums, int start, int end) {if(start >= end) return;// 递归结束条件// 分解int pivot = nums[start + new Random().nextInt(end - start + 1)];int l = start - 1, r = end + 1, i = start;while(i < r) {int cur = nums[i];if(cur < pivot) swap(nums, ++l, i++);else if(cur == pivot) ++i;else swap(nums, --r, i);}// [start, l]  [l+1, r-1]  [r, end]// 递归解决qsort(nums, start, l);qsort(nums, r, end);}private void swap(int[] nums,int i, int j) {int tmp = nums[i]; nums[i] = nums[j]; nums[j] = tmp;}
}

• 效率明显提升

四.快速选择算法

快速选择算法是基于快速排序优化版本的一种时间复杂度可达到O(N)的选择算法,使用场景为第K大/前K大之类的选择问题

01.数组中的第K个最大的元素
链接:https://leetcode.cn/problems/kth-largest-element-in-an-array/
分析

• 暴力解法就是直接使用sort进行排序,然后返回第K大即可
• 时间复杂度:O(N*logN)
• 空间复杂度:O(logN)递归产生的栈调用

接下来采用快速选择算法,实现O(N)的时间复杂度
代码:

class Solution {public int findKthLargest(int[] nums, int k) {return qsort(nums, 0, nums.length - 1, k);}private int qsort(int[] nums, int start, int end, int k) {if(start >= end) return nums[start];int pivot = nums[start + new Random().nextInt(end - start + 1)];// 数组分三块  <pivot  ==pivot  >pivotint l = start - 1, r = end + 1, i = start;while(i < r) {if(nums[i] < pivot) swap(nums, ++l, i++);else if(nums[i] == pivot) ++i;else swap(nums, --r, i);}// [start, l]  [l+1, r - 1]  [r, end]int c = end - r + 1, b = r - 1 - (l + 1) + 1, a = l - start + 1;// 分情况讨论  进行选择if(c >= k) return qsort(nums, r, end, k);else if(b + c >= k) return pivot;else return qsort(nums, start, l, k - b - c);// 找较小区间的第(k-b-c)大}private void swap(int[] arr, int i, int j) {int tmp = arr[i]; arr[i] = arr[j]; arr[j] = tmp;}
}

• 快速选择算法和快速排序的思想很像,不同点在于快速选择算法只对每次parttion结果的一部分区间进行递归,而不是像快速排序一样对整个区间进行递归,所以快速选择算法的时间复杂度降到了O(N)