【C++】B树及其实现
写目录
- 一、B树的基本概念
- 1.引入
- 2.B树的概念
- 二、B树的实现
- 1.B树的定义
- 2.B树的查找
- 3.B树的插入操作
- 4.B树的删除
- 5.B树的遍历
- 6.B树的高度
- 7.整体代码
- 三、B+树和B*树
- 1.B+树
- 2.B*树
- 3.总结
一、B树的基本概念
1.引入
我们已经学习过二叉排序树、AVL树和红黑树三种树形查找结构,但上述结构适用于数据量相对不是很大,能够一次性放进内存中,进行数据查找的场景。如果数据量非常大,比如由100G数据,无法一次放进内存中,那就只能放在磁盘上了。此时想要搜索数据就需要将存放关键字及其映射的数据的地址放到内存中的搜索树的节点中,那么要访问数据时,先取这个地址去磁盘访问数据。
但是由于磁盘访问的速度很慢,对于上述树形查找结构来说就是需要logN次的IO,这是一个很难接受的结果。
那么如何加速对数据的访问呢?
- 提高IO的速度(SSD相比传统机械硬盘是快了不少,但还是没有得到本质性的提升)
- 降低树的高度——多路平衡查找树
2.B树的概念
B树是一种平衡的多叉树。一颗m阶(m>2)的B树,是一棵的m路平衡搜索树,它可以是空树或者满足以下性质:
- 根节点至少有两个孩子。
- 每个分支节点都包含k-1个关键字和k个孩子,其中 ceil(m/2) ≤ k ≤ m (ceil是向上取整函数)。
- 每个叶子节点都包含k-1个关键字,其中 ceil(m/2) ≤ k ≤ m。
- 所有的叶子节点都在同一层。
- 每个节点中的关键字从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域划分。
- 每个结点的结构为:(n,A0,K1,A1,K2,A2,… ,Kn,An)其中,Ki(1≤i≤n)为关键字,且Ki<Ki+1(1≤i≤n-1)。Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。
n为结点中关键字的个数,满足ceil(m/2)-1≤n≤m-1。
二、B树的实现
1.B树的定义
为了方便学习,我们在这里先将m设为3,这时每个结点能存2个关键字和3个孩子。不过为了方便后续插入,分别额外多开了一个空间。

template<class K, size_t M>
struct BTreeNode
{K _keys[M]; // 用于存储关键字BTreeNode<K, M>* _subs[M + 1]; // 用于存储孩子BTreeNode<K, M>* _parent; size_t _n; // 存储当前孩子的数量BTreeNode(){for (size_t i = 0; i < M; ++i){_keys[i] = K();_subs[i] = nullptr;}_subs[M] = nullptr;_parent = nullptr;_n = 0;}
};
2.B树的查找
查找的具体步骤应该是先进入根结点,如果等于data1,则返回,如果小于data1,则进入child1,如果大于data1则++i,此时i指向data2,若小于data2,则进入child2,若大于data2,则进入child3。
pair<Node*, int> Find(const K& key)
{Node* parent = nullptr;Node* cur = _root;while (cur){size_t i = 0;while (i < cur->_n) // 在当前结点进行查找{if (key < cur->_keys[i]) // 如果小于则进入与当前下标相同的孩子{break;}else if (key > cur->_keys[i]) //如果大于则++i{++i;}else{return make_pair(cur, i); // 找到了就返回当前结点以及该关键字所在的位置}}parent = cur;cur = cur->_subs[i];}return make_pair(parent, -1); //找不到返回父结点
}
3.B树的插入操作
用序列{53, 139, 75, 49, 145, 36, 101}构建B树的过程如下:







插入过程总结:
- 如果树为空,直接插入新节点中,该节点为树的根节点
- 树非空,找待插入元素在树中的插入位置(注意:找到的插入节点位置一定在叶子节点中)
- 检测是否找到插入位置(假设树中的key唯一,即该元素已经存在时则不插入)
- 按照插入排序的思想将该元素插入到找到的节点中
- 检测该节点是否满足B-树的性质:即该节点中的元素个数是否等于M,如果小于则满足
- 如果插入后节点不满足B树的性质,需要对该节点进行分裂:
- 申请新节点
- 找到该节点的中间位置
- 将该节点中间位置右侧的元素以及其孩子搬移到新节点中
- 将中间位置元素以及新节点往该节点的双亲节点中插入,即继续4
- 如果向上已经分裂到根节点的位置,插入结束
// 插入操作中用到的函数
void InsertKey(Node* node, const K& key, Node* child) // 插入新关键字
{int end = node->_n - 1;while (end >= 0){if (key < node->_keys[end]){node->_keys[end + 1] = node->_keys[end];node->_subs[end + 2] = node->_subs[end + 1];--end;}else{break;}}node->_keys[end + 1] = key;node->_subs[end + 2] = child;if (child){child->_parent = node;}++node->_n;
}
// B树的插入
bool Insert(const K& key)
{if (_root == nullptr) //如果根结点为空{_root = new Node;_root->_keys[0] = key;++_root->_n;return true;}pair<Node*, int> ret = Find(key); // 借助查找操作来判定是否存在要插入的值if (ret.second >= 0) // 如果不存在则可以找到要进行插入的位置{return false;}Node* parent = ret.first;K newKey = key;Node* child = nullptr;while (1){InsertKey(parent, newKey, child); // 先利用插入排序的方法进行插入if (parent->_n < M) // 如果没有破坏B树的性质则返回true{return true;}else // 否则进行分裂操作{size_t mid = M / 2;Node* brother = new Node;size_t i = mid + 1;size_t j = 0;for (; i < M; ++i) // 把一半的数据分给新建的兄弟结点{brother->_keys[j] = parent->_keys[i];brother->_subs[j] = parent->_subs[i];if (parent->_subs[i]){parent->_subs[i]->_parent = brother;}++j;// 拷走重置一下方便观察parent->_keys[i] = K();parent->_subs[i] = nullptr;}brother->_subs[j] = parent->_subs[i];if (parent->_subs[i]){parent->_subs[i]->_parent = brother;}parent->_subs[i] = nullptr;brother->_n = j;parent->_n -= (brother->_n + 1);K midKey = parent->_keys[mid];parent->_keys[mid] = K();if (parent->_parent == nullptr) // 如果没有父结点,则新建{_root = new Node;_root->_keys[0] = midKey;_root->_subs[0] = parent;_root->_subs[1] = brother;_root->_n = 1;parent->_parent = _root;brother->_parent = _root;break;}else // 有父结点则将插入排序的参数修改,然后回到循环开始插入{newKey = midKey;child = brother;parent = parent->_parent;}}}return true;
}
B树插入的代码实现非常复杂,需要十分细心,要注意对结点的维护。
4.B树的删除
B树的删除分为3种情况:
- 直接删除关键字:若删除当前关键字后仍然满足B树定义,则直接删除该关键字。
- 兄弟够借:若再删除一个关键字就会破坏B树定义,并且左,右兄弟的关键字个数大于等于ceil(m/2),则需要调整该结点、右(或左)兄弟结点及其父结点(父子换位法),以达到新的平衡。
- 兄弟不够借:若左、右兄弟结点的关键字个数都不足以被借,则将关键字删除后与左(或右)兄弟结点及父结点的关键字进行合并。
由于B树的删除用代码实现非常复杂,就不多讲了。
5.B树的遍历
B树的遍历就不难了,与查找的过程类比即可。
void _InOrder(Node* cur)
{if (cur == nullptr)return;// 左 根 左 根 ... 右size_t i = 0;for (; i < cur->_n; ++i){_InOrder(cur->_subs[i]); // 左子树cout << cur->_keys[i] << " "; // 根}_InOrder(cur->_subs[i]); // 最后的那个右子树
}void InOrder()
{_InOrder(_root);
}
6.B树的高度
B树的效率取决于B树的高度,因为磁盘存取次数与高度成正比。
若n>=1,则对任意一颗包含n个关键字、高度为h、阶数为m的B树:
- 若让每个结点中的关键字个数达到最多,则容纳同样多关键字的B树的高度达到最小。因为B树种每个结点最多有m棵子树,m-1个关键字,所以在一颗高度为h的m阶B树中关键字的个数应满足 n < = ( m − 1 ) ( 1 + m + m 2 + . . . + m h − 1 ) = m h − 1 n<=(m-1)(1+m+m^2+...+m^{h-1})=m^h-1 n<=(m−1)(1+m+m2+...+mh−1)=mh−1,因此有 h > = l o g m ( n + 1 ) h>=log_m(n+1) h>=logm(n+1)
- 若让每个结点中的关键字个数达到最少,则容纳同样多关键字的B树高度达到最大。第一层至少有1个结点;第二层至少有两个结点;除根结点外的每个非叶结点至少有ceil(m/2)棵子树,则第三层至少有2ceil(m/2)个结点……第h+1层至少有 2 ( c e i l ( m / 2 ) ) h − 1 2(ceil(m/2))^{h-1} 2(ceil(m/2))h−1个结点,注意到第h+1层是不包含任何信息的叶结点。对于关键字个数为n的B树,叶结点即查找不成功的结点为n+1,由此有 n + 1 > = 2 ( c e i l ( m / 2 ) ) h − 1 n+1>=2(ceil(m/2))^{h-1} n+1>=2(ceil(m/2))h−1,即 h < = l o g c e i l ( m / 2 ) ( ( n + 1 ) / 2 ) + 1 h<=log_{ceil(m/2)}((n+1)/2)+1 h<=logceil(m/2)((n+1)/2)+1。
7.整体代码
#include <iostream>
using namespace std;template<class K, size_t M>
struct BTreeNode
{K _keys[M];BTreeNode<K, M>* _subs[M + 1];BTreeNode<K, M>* _parent;size_t _n;BTreeNode(){for (size_t i = 0; i < M; ++i){_keys[i] = K();_subs[i] = nullptr;}_subs[M] = nullptr;_parent = nullptr;_n = 0;}
};template<class K, size_t M>
class BTree
{typedef BTreeNode<K, M> Node;
public:pair<Node*, int> Find(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){size_t i = 0;while (i < cur->_n) // 在当前结点进行查找{if (key < cur->_keys[i]) // 如果小于则进入与当前下标相同的孩子{break;}else if (key > cur->_keys[i]) //如果大于则++i{++i;}else{return make_pair(cur, i); // 找到了就返回当前结点以及该关键字所在的位置}}parent = cur;cur = cur->_subs[i];}return make_pair(parent, -1); //找不到返回父结点}void InsertKey(Node* node, const K& key, Node* child) // 插入新关键字{int end = node->_n - 1;while (end >= 0){if (key < node->_keys[end]){node->_keys[end + 1] = node->_keys[end];node->_subs[end + 2] = node->_subs[end + 1];--end;}else{break;}}node->_keys[end + 1] = key;node->_subs[end + 2] = child;if (child){child->_parent = node;}++node->_n;}bool Insert(const K& key){if (_root == nullptr) //如果根结点为空{_root = new Node;_root->_keys[0] = key;++_root->_n;return true;}pair<Node*, int> ret = Find(key); // 借助查找操作来判定是否存在要插入的值if (ret.second >= 0) // 如果不存在则可以找到要进行插入的位置{return false;}Node* parent = ret.first;K newKey = key;Node* child = nullptr;while (1){InsertKey(parent, newKey, child); // 先利用插入排序的方法进行插入if (parent->_n < M) // 如果没有破坏B树的性质则返回true{return true;}else // 否则进行分裂操作{size_t mid = M / 2;Node* brother = new Node;size_t i = mid + 1;size_t j = 0;for (; i < M; ++i) // 把一半的数据分给新建的兄弟结点{brother->_keys[j] = parent->_keys[i];brother->_subs[j] = parent->_subs[i];if (parent->_subs[i]){parent->_subs[i]->_parent = brother;}++j;// 拷走重置一下方便观察parent->_keys[i] = K();parent->_subs[i] = nullptr;}brother->_subs[j] = parent->_subs[i];if (parent->_subs[i]){parent->_subs[i]->_parent = brother;}parent->_subs[i] = nullptr;brother->_n = j;parent->_n -= (brother->_n + 1);K midKey = parent->_keys[mid];parent->_keys[mid] = K();if (parent->_parent == nullptr) // 如果没有父结点,则新建{_root = new Node;_root->_keys[0] = midKey;_root->_subs[0] = parent;_root->_subs[1] = brother;_root->_n = 1;parent->_parent = _root;brother->_parent = _root;break;}else // 有父结点则将插入排序的参数修改,然后回到循环开始插入{newKey = midKey;child = brother;parent = parent->_parent;}}}return true;}void _InOrder(Node* cur){if (cur == nullptr)return;// 左 根 左 根 ... 右size_t i = 0;for (; i < cur->_n; ++i){_InOrder(cur->_subs[i]); // 左子树cout << cur->_keys[i] << " "; // 根}_InOrder(cur->_subs[i]); // 最后的那个右子树}void InOrder(){_InOrder(_root);}
private:Node* _root = nullptr;
};void TestBtree()
{int a[] = { 53, 139, 75, 49, 145, 36, 101 };BTree<int, 3> t;for (auto e : a){t.Insert(e);}t.InOrder();
}
三、B+树和B*树
1.B+树
B+树是B树的变形,是在B树基础上优化的多路平衡搜索树,B树的规则跟B树基本类似,但是又在B树的基础上做了以下几点改进优化:
- 分支节点的子树指针与关键字个数相同
- 分支节点的子树指针p[i]指向关键字值大小在[k[i],k[i+1])区间之间
- 所有叶子节点增加一个链接指针链接在一起
- 所有关键字及其映射数据都在叶子节点出现

B+树的特性:
- 所有关键字都出现在叶子结点的链表中,且链表中的结点都是有序的。
- 不可能在分支结点中命中。
- 分支结点相当于是叶子结点的索引,叶子结点才是存储数据的数据层。
B+树的分裂:
当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增
加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向
兄弟的指针。
2.B*树
B*树是B+树的变形,在B+树的非根和非叶子节点再增加指向兄弟节点的指针。

B*树的分裂:
当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结
点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如
果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父
结点增加新结点的指针。
所以,B*树分配新结点的概率比B+树要低,空间使用率更高;
3.总结
通过以上介绍,大致将B树,B+树,B*树总结如下:
- B树:有序数组+平衡多叉树;
- B+树:有序数组链表+平衡多叉树;
- B*树:一棵更丰满的,空间利用率更高的B+树。
相关文章:

【C++】B树及其实现
写目录 一、B树的基本概念1.引入2.B树的概念 二、B树的实现1.B树的定义2.B树的查找3.B树的插入操作4.B树的删除5.B树的遍历6.B树的高度7.整体代码 三、B树和B*树1.B树2.B*树3.总结 一、B树的基本概念 1.引入 我们已经学习过二叉排序树、AVL树和红黑树三种树形查找结构&#x…...

C++(Qt)-GIS开发-QGraphicsView显示瓦片地图简单示例
C(Qt)-GIS开发-QGraphicsView显示瓦片地图简单示例 文章目录 C(Qt)-GIS开发-QGraphicsView显示瓦片地图简单示例1、概述2、实现效果3、主要代码4、源码地址 更多精彩内容👉个人内容分类汇总 👈👉GIS开发 👈 1、概述 支持多线程加…...

CTFShow的RE题(三)
数学不及格 strtol 函数 long strtol(char str, char **endptr, int base); 将字符串转换为长整型 就是解这个方程组了 主要就是 v4, v9的关系, 3v9-(v10v11v12)62d10d4673 v4 v12 v11 v10 0x13A31412F8C 得到 3*v9v419D024E75FF(1773860189695) 重点&…...
WordPress主题开发进群付费主题v1.1.2 多种引流方式
全新前端UI界面,多种前端交互特效让页面不再单调,进群页面群成员数,群成员头像名称,每次刷新页面随机更新不重复,最下面评论和点赞也是如此随机刷新不重复 进群页面简介,群聊名称,群内展示&…...
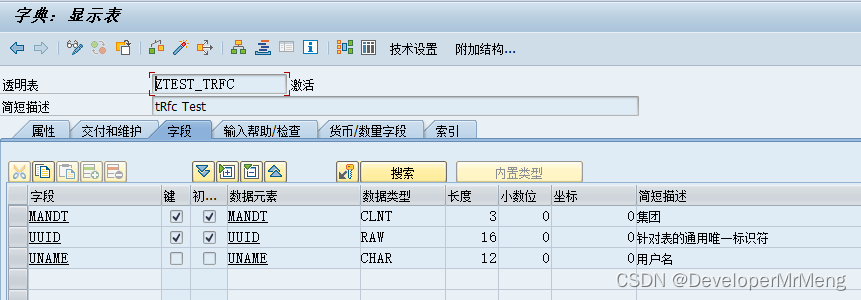
SAP中的 UPDATA TASK 和 BACKGROUND TASK
前言: 记录这篇文章起因是调查生产订单报工问题引申出来的一个问题,后来再次调查后了解了其中缘由,大概记录以下,如有不对,欢迎指正。问题原贴如下: SAP CO11N BAPI_PRODORDCONF_CREATE_TT连续报工异步更…...
UDP协议:独特之处及其在网络通信中的应用
在网络通信领域,UDP(用户数据报协议,User Datagram Protocol)是一种广泛使用的传输层协议。与TCP(传输控制协议,Transmission Control Protocol)相比,UDP具有其独特的特点和适用场景…...
及Python和MATLAB实现)
支持向量机(Support Vector Machine,SVM)及Python和MATLAB实现
支持向量机(Support Vector Machine,SVM)是一种经典的机器学习算法,广泛应用于模式识别、数据分类和回归分析等领域。SVM的背景可以追溯到1990s年代,由Vladimir Vapnik等人提出,并在之后不断发展和完善。 …...
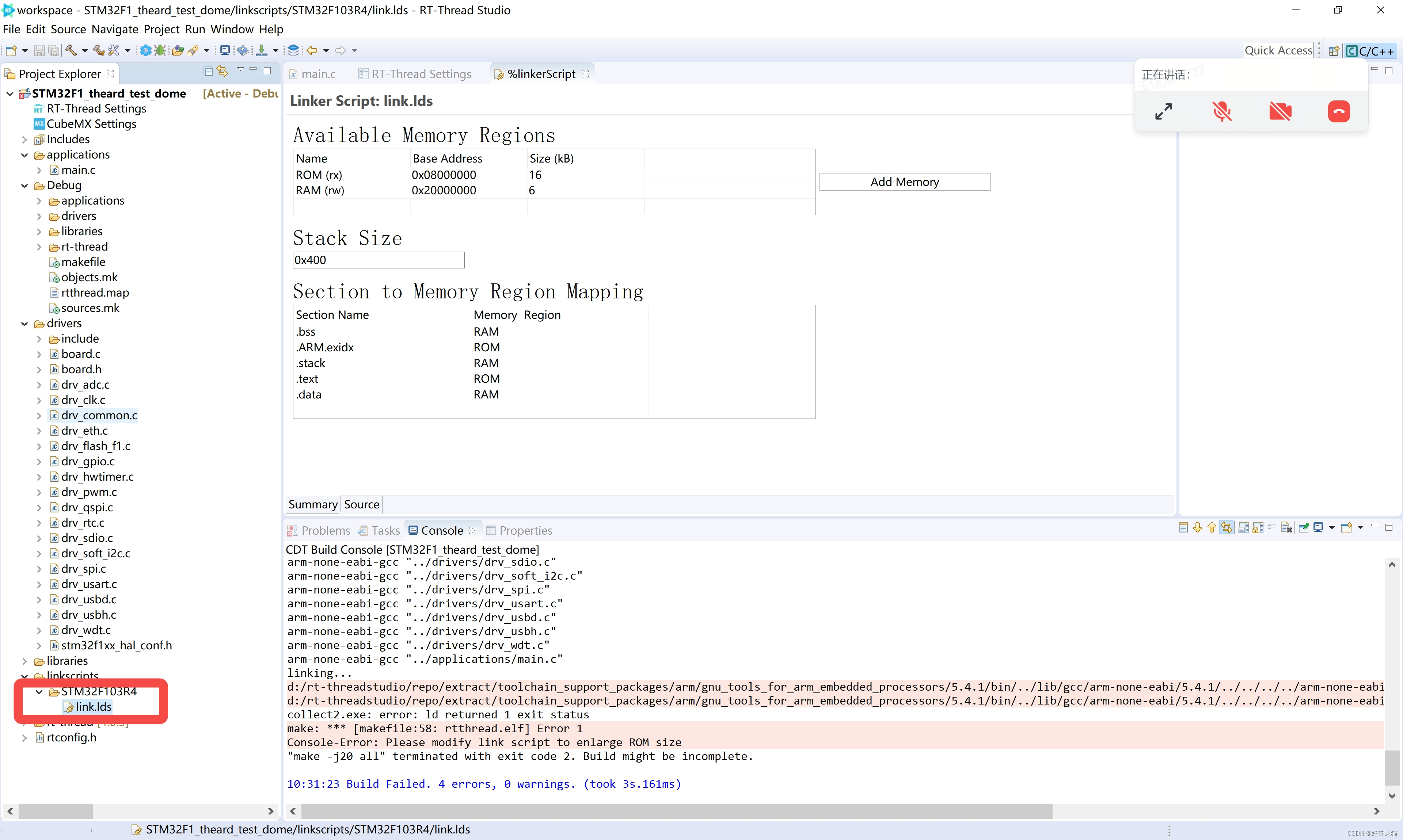
【RT-thread studio 下使用STM32F103-学习sem-信号量-初步使用-线程之间控制-基础样例】
【RT-thread studio 下使用STM32F103-学习sem-信号量-初步使用-线程之间控制-基础样例】 1、前言2、环境3、事项了解(1)了解sem概念-了解官网消息(2)根据自己理解,设计几个使用方式(3)不建议运行…...

使用nodejs输出著作权申请所需的word版源码
使用nodejs输出著作权申请所需的word版源码 背景 软件著作权申请需要提供一份80页的word版源代码,如果手工复制源码到word文档中,工作量将无聊到让任何一个DAO人员血压爆表,因此我们不得不编写一个简单的文本处理代码,通过自动方…...

[Vite]vite-plugin-react和vite-plugin-react-swc插件原理了解
[Vite]vite-plugin-react和vite-plugin-react-swc插件原理了解 共同的作用 JSX 支持:插件为 React 应用程序中的 JSX 语法提供支持,确保它可以被正确地转换为 JavaScript。Fast Refresh:提供热更新功能,当应用程序在开发服务器上…...

记一次使用“try-with-resources“的语法导致的BUG
背景描述 最近使用try-catch的时候遇到了一个问题,背景是这样的:当第一次与数据库建立连接以后执行查询完毕并没有手动关闭连接,但是当我第二次获取连接的时候报错了,显示数据库连接失败,连接已经关闭。 org.postgres…...

用Excel处理数据图像,出现交叉怎么办?
一、问题描述 用excel制作X-Y散点图,意外的出现了4个交叉点,而实际上的图表数据是没有交叉的。 二、模拟图表 模拟部分数据,并创建X-Y散点图,数据区域,X轴数据是依次增加的,因此散点图应该是没有交叉的。…...

SpringBoot | 大新闻项目后端(redis优化登录)
该项目的前篇内容的使用jwt令牌实现登录认证,使用Md5加密实现注册,在上一篇:http://t.csdnimg.cn/vn3rB 该篇主要内容:redis优化登录和ThreadLocal提供线程局部变量,以及该大新闻项目的主要代码。 redis优化登录 其实…...

ESP32——物联网小项目汇总
商品级ESP32智能手表 [文章链接] 用ESP32,做了个siri?!开源了! [文章链接]...

flutter:监听路由的变化
问题 当从路由B页面返回路由A页面后,A页面需要进行数据刷新。因此需要监听路由变化 解决 使用RouteObserver进行录音监听 创建全局变量,不在任何类中 final RouteObserver<PageRoute> routeObserver RouteObserver<PageRoute>();在mai…...

Linux多进程和多线程(六)进程间通信-共享内存
多进程(六) 共享内存共享内存的创建 示例: 共享内存删除 共享内存映射 共享内存映射的创建解除共享内存映射示例:写入和读取共享内存中的数据 写入: ### 读取: 大致操作流程: 多进程(六) 共享内存 共享内存是将分配的物理空间直接映射到进程的⽤户虚拟地址空间中, 减少数据在…...

ruoyi后台修改
一、日志文件过大分包 \ruoyi-admin\src\main\resources\logback.xml <!-- 系统日志输出 --> <appender name"file_info" class"ch.qos.logback.core.rolling.RollingFileAppender"><file>${log.path}/sys-info.log</file><!…...

macOS查看系统日志的方法
1、command空格键打开搜索框,输入‘控制台’并打开 2、选择日志报告,根据日期打开自己需要的文件就可以...

数字信号处理及MATLAB仿真(3)——采样与量化
今天写主要来编的程序就是咱们AD变换的两个步骤。一个是采样,还有一个是量化。大家可以先看看,这一过程当中的信号是如何变化的。信号的变换图如下。 先说说采样,采样是将连续时间信号转换为离散时间信号的过程。在采样过程中,连续…...
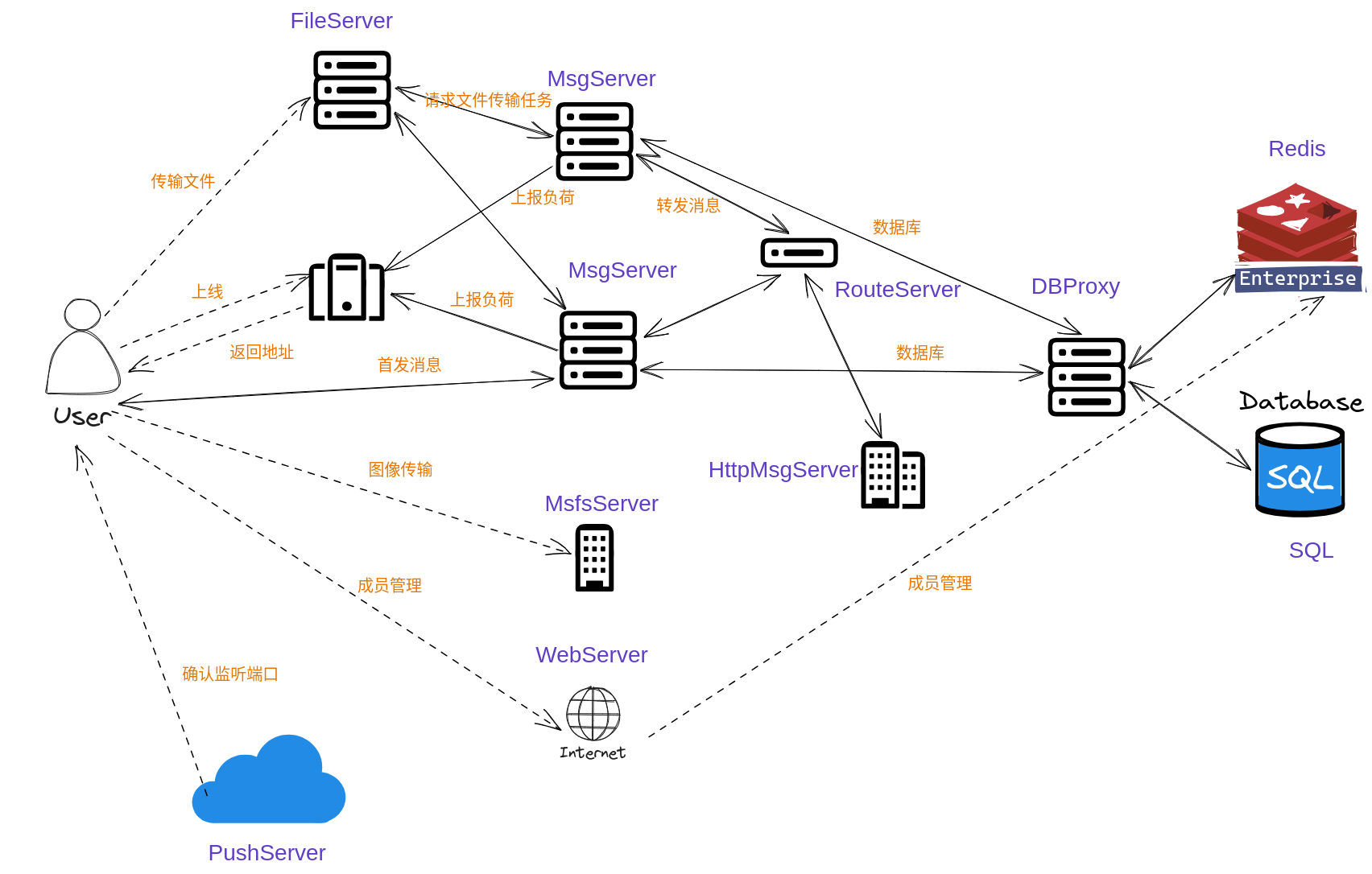
云端AI大模型群体智慧后台架构思考
1 大模型的调研 1.1 主流的大模型 openai-chatgpt 阿里巴巴-通义千问 一个专门响应人类指令的大模型。我是效率助手,也是点子生成机,我服务于人类,致力于让生活更美好。 百度-文心一言(千帆大模型) 文心一言"…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
