QT slots 函数
文章目录
- 概述
- 小结
概述
在Qt中,slots 是一种特殊的成员函数,它们可以与对象发出的信号连接。当信号被触发时,连接的槽函数会被调用。
来个简单的示例吧,如下图:
#include <QObject>
#include <QDebug>class MyClass : public QObject {Q_OBJECTpublic:MyClass() {// 连接信号和槽connect(this, &MyClass::someSignal, this, &MyClass::someSlot);}signals:void someSignal(); // 声明一个无参数的信号public slots:void someSlot() { // 声明一个无参数的槽函数qDebug() << "someSlot called!";}void anotherSlot(int value) { // 声明一个有参数的槽函数qDebug() << "anotherSlot called with value:" << value;}
};int main() {MyClass obj;obj.emit someSignal(); // 发出信号obj.anotherSlot(42); // 直接调用槽函数return 0;
}
如果对C++熟悉,可以直接把connect函数改成其他格式,如下是lamda表达式:
#include <QObject>
#include <QDebug>class MyClass : public QObject {Q_OBJECTpublic:MyClass() {// 连接信号和槽connect(this, &MyClass::someSignal, this, [this](){qDebug() << "someSlot Called!"; //1将调用写到lamda中//emit anotherSlot(42); // 2也可以调用另外一个slot函数});}signals:void someSignal(); // 声明一个无参数的信号public slots:// void someSlot() { // 声明一个无参数的槽函数// qDebug() << "someSlot called!";// }void anotherSlot(int value) { // 声明一个有参数的槽函数qDebug() << "anotherSlot called with value:" << value;}
};int main() {MyClass obj;obj.emit someSignal(); // 发出信号obj.anotherSlot(42); // 直接调用槽函数return 0;
}
小结
这篇主要写了qt slots函数,不熟悉qt经常忘记这个,其余的内容对c++程序来说就容易驾驭多了。OK,下篇写点有用的,好玩的内容。
相关文章:

QT slots 函数
文章目录 概述小结 概述 在Qt中,slots 是一种特殊的成员函数,它们可以与对象发出的信号连接。当信号被触发时,连接的槽函数会被调用。 来个简单的示例吧,如下图: #include <QObject> #include <QDebug>…...

pycharm如何使用jupyter
目录 配置jupyter新建jupyter文件别人写的方法(在pycharm种安装,在网页中使用) pycharm专业版 配置jupyter 在pycharm终端启动一个conda虚拟环境,输入 conda install jupyter会有很多前置包需要安装: 新建jupyter…...

机器学习——无监督学习(k-means算法)
1、K-Means聚类算法 K表示超参数个数,如分成几个类别,K值就取多少。若无需求,可使用网格搜索找到最佳的K。 步骤: 1、随机设置K个特征空间内的点作为初始聚类中心; 2、对于其他每个点计算到K个中心的距离,…...

强化学习-6 DDPG、PPO、SAC算法
文章目录 1 DPG方法2 DDPG算法3 DDPG算法的优缺点4 TD3算法4.1 双Q网络4.2 延迟更新4.3 噪声正则 5 附15.1 Ornstein-Uhlenbeck (OU) 噪声5.1.1 定义5.1.2 特性5.1.3 直观理解5.1.4 数学性质5.1.5 代码示例5.1.6 总结 6 重要性采样7 PPO算法8 附28.1 重要性采样方差计算8.1.1 公…...

vue3实现多表头列表el-table,拖拽,鼠标滑轮滚动条优化
需求背景解决效果index.vue 需求背景 需要实现多表头列表的用户体验优化 解决效果 index.vue <!--/** * author: liuk * date: 2024-07-03 * describe:**** 多表头列表 */--> <template><el-table ref"tableRef" height"calc(100% - 80px)&qu…...

Micron近期发布了32Gb DDR5 DRAM
Micron Technology近期发布了一项内存技术的重大突破——一款32Gb DDR5 DRAM芯片,这项创新不仅将存储容量翻倍,还显著提升了针对人工智能(AI)、机器学习(ML)、高性能计算(HPC)以及数…...

SQL Server时间转换
第一种:format --转化成年月日 select format( GETDATE(),yyyy-MM-dd) --转化年月日,时分秒,这里的HH指24小时的,hh是12小时的 select format( GETDATE(),yyyy-MM-dd HH:mm:ss) --转化成时分秒的,这里就不一样的&…...

kubernetes集群部署:node节点部署和CRI-O运行时安装(三)
关于CRI-O Kubernetes最初使用Docker作为默认的容器运行时。然而,随着Kubernetes的发展和OCI标准的确立,社区开始寻找更专门化的解决方案,以减少复杂性和提高性能。CRI-O的主要目标是提供一个轻量级的容器运行时,它可以直接运行O…...

03:Spring MVC
文章目录 一:Spring MVC简介1:说说自己对于Spring MVC的了解?1.1:流程说明: 一:Spring MVC简介 Spring MVC就是一个MVC框架,Spring MVC annotation式的开发比Struts2方便,可以直接代…...

玩转springboot之springboot注册servlet
springboot注册servlet 有时候在springboot中依然需要注册servlet,filter,listener,就以servlet为例来进行说明,另外两个也都类似 使用WebServlet注解 在servlet3.0之后,servlet注册支持注解注册,而不需要在…...

推荐好玩的工具之OhMyPosh使用
解除禁止脚本 Set-ExecutionPolicy RemoteSigned 下载Oh My Posh winget install oh-my-posh 或者 Install-Module oh-my-posh -Scope AllUsers 下载Git提示 Install-Module posh-git -Scope CurrentUser 或者 Install-Module posh-git -Scope AllUser 下载命令提示 Install-Mo…...
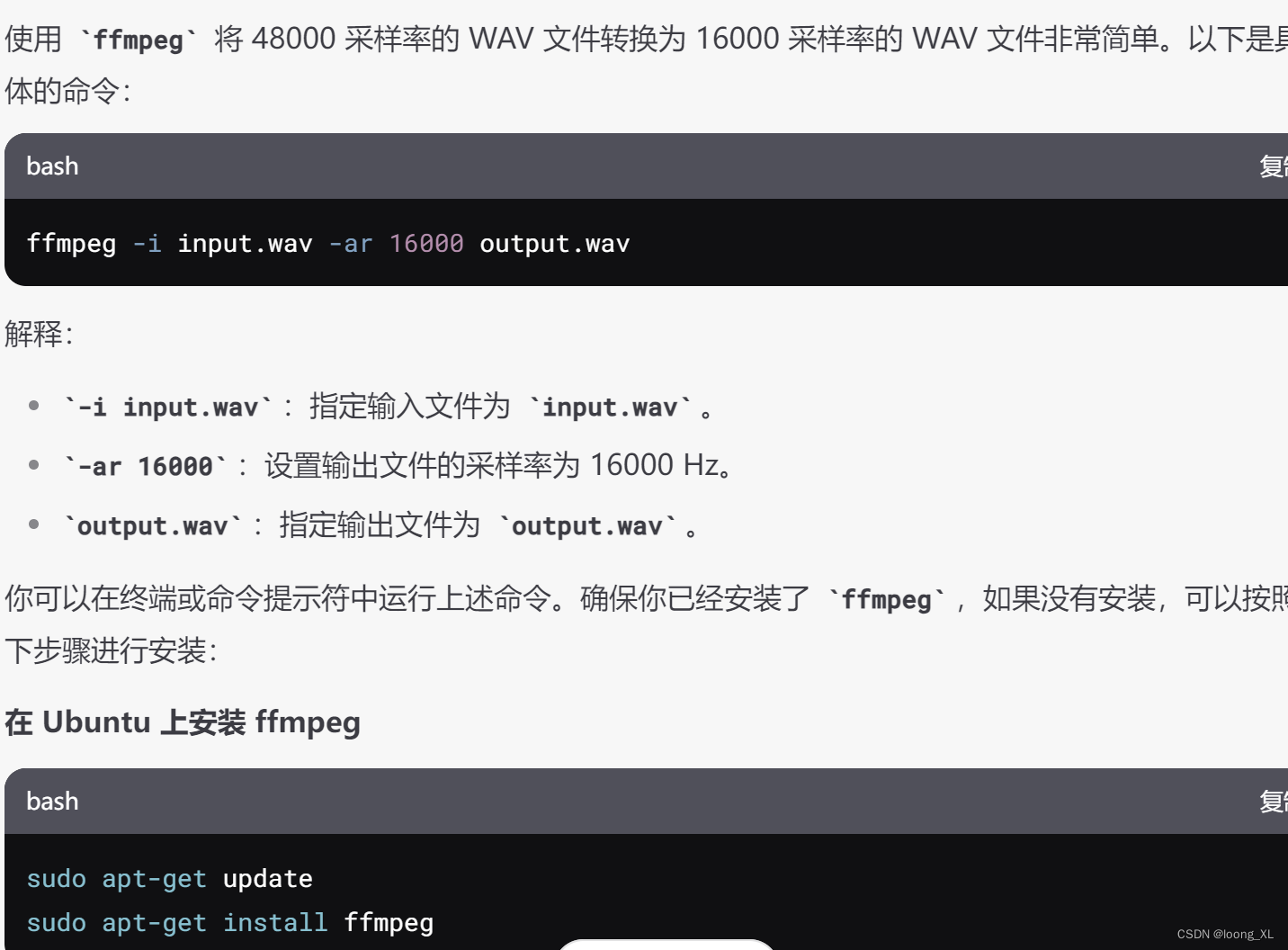
pydub、ffmpeg 音频文件声道选择转换、采样率更改
快速查看音频通道数和每个通道能力判断具体哪个通道说话;一般能量大的那个算是说话 import wave from pydub import AudioSegment import numpy as npdef read_wav_file(file_path):with wave.open(file_path, rb) as wav_file:params wav_file.getparams()num_cha…...

0803实操-Windows Server系统管理
Windows Server系统管理 系统管理与基础配置 查看系统信息、更改计算机名称 网络配置 启用网络发现 Windows启用网络发现是指在网络设置中启用一个功能,该功能允许您的计算机在网络上识别和访问其他设备和计算机。具体来说,启用网络发现后ÿ…...

使用Java构建物联网应用的最佳实践
使用Java构建物联网应用的最佳实践 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿! 随着物联网(IoT)技术的快速发展,越来越…...
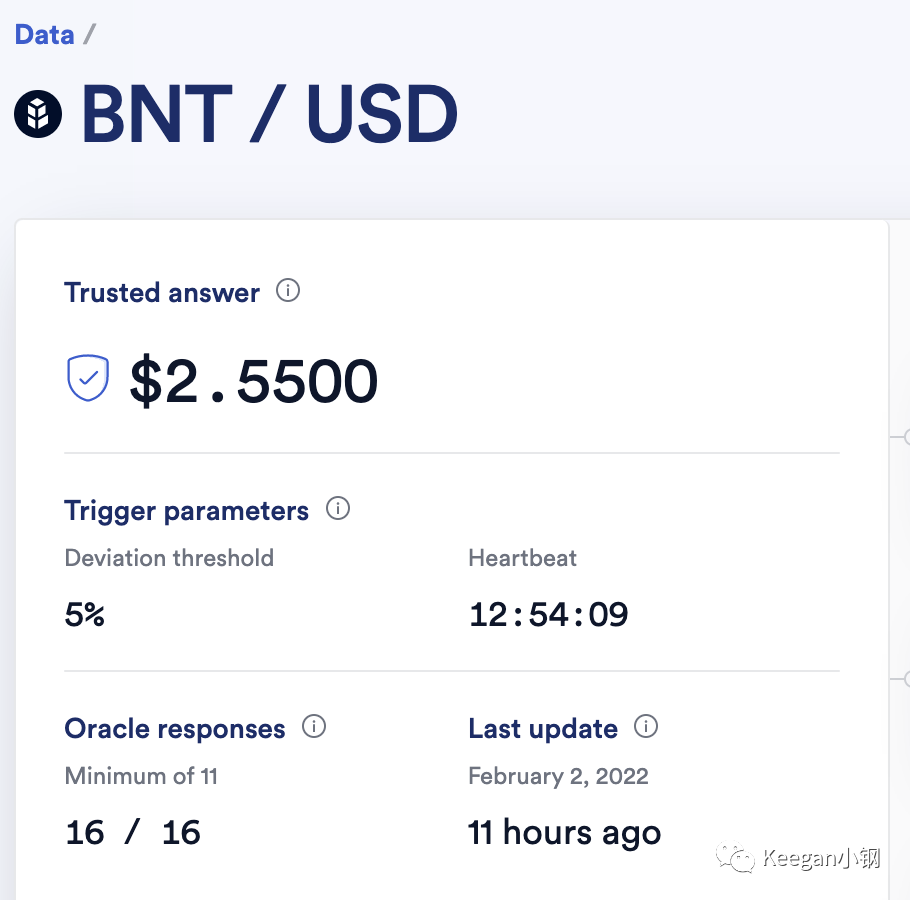
价格预言机的使用总结(一):Chainlink篇
文章首发于公众号:Keegan小钢 前言 价格预言机已经成为了 DeFi 中不可获取的基础设施,很多 DeFi 应用都需要从价格预言机来获取稳定可信的价格数据,包括借贷协议 Compound、AAVE、Liquity ,也包括衍生品交易所 dYdX、PERP 等等。…...
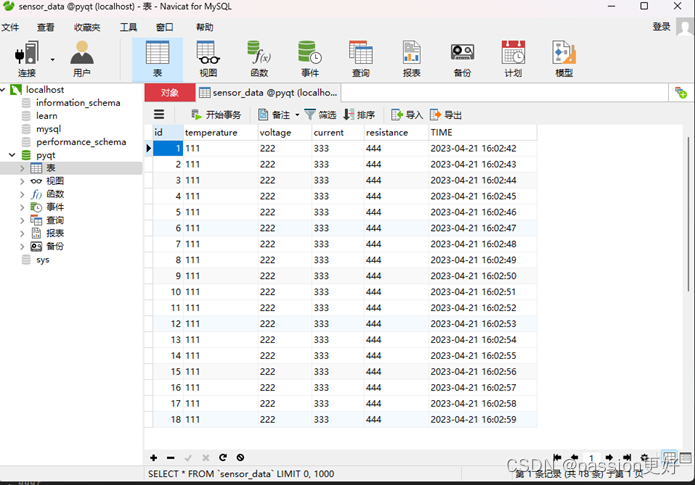
【Pyhton】读取寄存器数据到MySQL数据库
目录 步骤 modsim32软件配置 Navicat for MySQL 代码实现 步骤 安装必要的库:确保安装了pymodbus和pymysql。 配置Modbus连接:设置Modbus从站的IP地址、端口(对于TCP)或串行通信参数(对于RTU)。 连接M…...

jmeter-beanshell学习3-beanshell获取请求报文和响应报文
前后两个报文,后面报文要用前面报文的响应结果,这个简单,正则表达式或者json提取器,都能实现。但是如果后面报文要用前面请求报文的内容,感觉有点难。最早时候把随机数写在自定义变量,前后两个接口都用这个…...

【C++】B树及其实现
写目录 一、B树的基本概念1.引入2.B树的概念 二、B树的实现1.B树的定义2.B树的查找3.B树的插入操作4.B树的删除5.B树的遍历6.B树的高度7.整体代码 三、B树和B*树1.B树2.B*树3.总结 一、B树的基本概念 1.引入 我们已经学习过二叉排序树、AVL树和红黑树三种树形查找结构&#x…...

C++(Qt)-GIS开发-QGraphicsView显示瓦片地图简单示例
C(Qt)-GIS开发-QGraphicsView显示瓦片地图简单示例 文章目录 C(Qt)-GIS开发-QGraphicsView显示瓦片地图简单示例1、概述2、实现效果3、主要代码4、源码地址 更多精彩内容👉个人内容分类汇总 👈👉GIS开发 👈 1、概述 支持多线程加…...

CTFShow的RE题(三)
数学不及格 strtol 函数 long strtol(char str, char **endptr, int base); 将字符串转换为长整型 就是解这个方程组了 主要就是 v4, v9的关系, 3v9-(v10v11v12)62d10d4673 v4 v12 v11 v10 0x13A31412F8C 得到 3*v9v419D024E75FF(1773860189695) 重点&…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
