自动控制:反馈控制
自动控制:反馈控制
反馈控制(Feedback Control)是一种在控制系统中通过测量输出信号,并将其与期望信号进行比较,产生误差信号,再根据误差信号调整输入来达到控制目标的方法。反馈控制是自动控制系统中最常见和最重要的控制策略之一,广泛应用于工业、自动化、机器人、航空航天等各个领域。
反馈控制的基本原理
反馈控制的基本原理可以概括如下:
- 测量输出:通过传感器或测量装置,实时测量系统的输出信号。
- 计算误差:将测量得到的输出信号与期望的参考信号进行比较,计算误差信号。
- 控制律:根据预先设计的控制律(如比例-积分-微分控制器,PID),计算控制输入。
- 施加控制输入:将计算得到的控制输入施加到系统中,以减小误差,使输出信号逐渐趋近期望值。
反馈控制系统的基本框图如下:
+---------------------+| || 系统 || |+----------+----------+|v+---------+----------+| || 传感器/测量 || |+---------+----------+|v+----------+----------+| || 误差计算 || e = r - y || |+----------+----------+|v+----------+----------+| || 控制律 || |+----------+----------+|v+----------+----------+| || 控制输入 u || |+---------------------+
其中:
- r r r 是期望的参考信号
- y y y 是系统的实际输出信号
- e e e是误差信号,即 e = r − y e = r - y e=r−y
- u u u 是控制输入信号
反馈控制的优点
- 稳定性:反馈控制能够自动调节系统的输入,使系统稳定在期望的输出值附近,即使存在扰动或参数变化。
- 鲁棒性:反馈控制对系统参数的不确定性和外界扰动具有较强的鲁棒性,能够在一定程度上克服模型的不准确性。
- 自动校正:反馈控制能够根据误差自动调整控制输入,使系统输出迅速趋近期望值。
- 广泛适用性:反馈控制适用于各种类型的系统,包括线性系统和非线性系统、时不变系统和时变系统。
常见的反馈控制策略
比例控制(P控制)
比例控制(Proportional Control, P控制)是一种最简单的反馈控制策略。它根据误差信号的比例调整控制输入。其控制律如下:
u ( t ) = K p ⋅ e ( t ) u(t) = K_p \cdot e(t) u(t)=Kp⋅e(t)
其中, K p K_p Kp 是比例增益。
比例-积分-微分控制(PID控制)
PID控制是一种广泛应用的反馈控制策略,由比例控制、积分控制和微分控制三部分组成。其控制律如下:
u ( t ) = K p ⋅ e ( t ) + K i ∫ e ( t ) d t + K d ⋅ d e ( t ) d t u(t) = K_p \cdot e(t) + K_i \int e(t) \, dt + K_d \cdot \frac{d e(t)}{dt} u(t)=Kp⋅e(t)+Ki∫e(t)dt+Kd⋅dtde(t)
其中:
- K p K_p Kp是比例增益
- K i K_i Ki 是积分增益
- K d K_d Kd 是微分增益
滑模控制(Sliding Mode Control, SMC)
滑模控制是一种处理非线性系统和不确定性系统的有效控制策略。它通过设计一个滑模面,并驱动系统状态达到并保持在该滑模面上,从而实现控制目标。
反馈控制的应用
反馈控制在工业和日常生活中有着广泛的应用。例如:
- 温度控制:通过反馈控制,恒温器可以自动调节加热器的功率,使房间温度保持在设定值附近。
- 速度控制:在电动机控制中,反馈控制能够根据速度传感器的反馈信号,调整电动机的输入电压或电流,使电动机的转速保持在期望值。
- 自动驾驶:在自动驾驶系统中,反馈控制能够根据车辆的实际位置和速度,与预定的轨迹进行比较,调整转向角度和速度,使车辆沿着预定路线行驶。
Python代码示例
下面是一个简单的Python代码示例,演示反馈控制的基本原理。假设我们有一个简单的温度控制系统,通过反馈控制保持系统温度在期望值。
import numpy as np
import matplotlib.pyplot as plt# 定义系统参数
dt = 0.1 # 时间步长
t = np.arange(0, 10, dt) # 时间数组
n = len(t)# 初始化状态变量
temperature = np.zeros(n) # 系统温度
desired_temperature = np.ones(n) * 0 # 期望温度
external_disturbance = np.sin(t) * 10 # 外界扰动# 控制器参数
Kp = 2.0 # 比例增益
Ki = 1.0 # 积分增益
Kd = 0.5 # 微分增益# 初始化误差变量
e_prev = 0 # 上一时刻的误差
integral = 0 # 误差积分# 模拟系统
for i in range(1, n):# 计算误差e = desired_temperature[i] - temperature[i-1]# 误差积分integral += e * dt# 误差微分derivative = (e - e_prev) / dt# PID控制器u = Kp * e + Ki * integral + Kd * derivative# 更新系统温度temperature[i] = temperature[i-1] + (u + external_disturbance[i]) * dt# 更新上一时刻的误差e_prev = e# 绘制结果
plt.figure(figsize=(10, 4))
plt.plot(t, desired_temperature, label='Desired Temperature')
plt.plot(t, temperature, label='Actual Temperature')
plt.plot(t, external_disturbance, label='External Disturbance')
plt.xlabel('Time [s]')
plt.ylabel('Temperature')
plt.legend()
plt.title('Feedback Control for Temperature System')
plt.grid(True)
plt.show()

代码解释
- 系统参数和时间数组:定义了时间步长
dt和时间数组t,用来模拟系统在一段时间内的行为。 - 状态变量初始化:初始化了系统温度
temperature、期望温度desired_temperature和外界扰动external_disturbance。 - 控制器参数:定义了PID控制器的比例增益
Kp、积分增益Ki和微分增益Kd。 - 误差变量初始化:初始化了上一时刻的误差
e_prev和误差积分integral。 - 系统模拟:通过迭代计算,在每个时间步长内根据PID控制律计算控制输入,并更新系统温度。
- 结果绘制:使用
matplotlib绘制系统温度、期望温度和外界扰动的变化曲线。
结论
反馈控制是一种通过实时测量系统输出并根据误差调整输入的控制策略,能够有效地提高系统的稳定性、鲁棒性和控制精度。常见的反馈控制策略包括比例控制、比例-积分-微分控制(PID控制)和滑模控制。在实际应用中,反馈控制广泛用于温度控制、速度控制和自动驾驶等领域。结合Python代码示例,可以更直观地理解反馈控制的基本原理和实现方法。
相关文章:

自动控制:反馈控制
自动控制:反馈控制 反馈控制(Feedback Control)是一种在控制系统中通过测量输出信号,并将其与期望信号进行比较,产生误差信号,再根据误差信号调整输入来达到控制目标的方法。反馈控制是自动控制系统中最常…...
sqlite 数据库 介绍
文章目录 前言一、什么是 SQLite ?二、语法三、SQLite 场景四、磁盘文件 前言 下载 目前已经出到了, Version 3.46.0 SQLite,是一款轻型的数据库,是遵守ACID的关系型数据库管理系统,它包含在一个相对小的C库中。它是…...

【机器学习】机器学习重塑广告营销:精准触达,高效转化的未来之路
📝个人主页🌹:Eternity._ 🌹🌹期待您的关注 🌹🌹 ❀目录 📒1. 引言📙2. 机器学习基础与广告营销的结合🧩机器学习在广告营销中的核心应用领域🌹用…...

常见的Java运行时异常
常见的Java运行时异常 1、ArithmeticException(算术异常)2、ClassCastException (类转换异常)3、IllegalArgumentException (非法参数异常)4、IndexOutOfBoundsException (下标越界异常…...
CANoe的capl调用Qt制作的dll
闲谈 因为Qt封装了很多个人感觉很好用的库,所以一直想通过CAPL去调用Qt实现一些功能,但是一直没机会(网络上也没看到这方面的教程),这次自己用了两天,踩了很多坑,终于是做成了一个初步的调用方…...

论如何搭建属于自己的服务器?
在现如今的数字化时代中,为了能够搭建网站和运行应用程序,很多人选择搭建属于自己的服务器,下面我们就来了解一下如何搭建服务器吧! 搭建服务器我们首先需要选择适合自身需求的硬件设备,其中包含内存、CPU和存储等配置…...

【C++ OpenCV】机器视觉-二值图像和灰度图像的膨胀、腐蚀、开运算、闭运算
原图 结果图 //包含头文件 #include <opencv2/opencv.hpp>//命名空间 using namespace cv; using namespace std;//全局函数声明部分//我的腐蚀运算 Mat Erode(Mat src, Mat Mask, uint32_t x0, uint32_t y0) {uint32_t x 0, y 0;Mat dst(src.rows, src.cols, CV_8U…...

STMF4学习笔记RTC(天空星)
前言:本篇笔记参考嘉立创文档,连接放在最后 #RTC相关概念定义 Real-Time Clock 缩写 RTC 翻译 实时时钟,是单片机片内外设的一种,作用于提供准确的时间还有日期,这个外设有独立的电源,当单片机停止供电…...

vue数组变化的侦测***
数组变化的侦测 变更方法 vue能够侦听响应式数组的变更方法,并在他们被调用时触发相关更新。这些变更方法包括: push()pop()shift()unshift()splice()sort()reverse() 替换一个数组 变更方法,顾名思义,就是会对调用他们的原数组进…...

k8s-第十节-Ingress
Ingress 介绍 Ingress 为外部访问集群提供了一个 统一 入口,避免了对外暴露集群端口;功能类似 Nginx,可以根据域名、路径把请求转发到不同的 Service。可以配置 https 跟 LoadBalancer 有什么区别? LoadBalancer 需要对外暴露…...
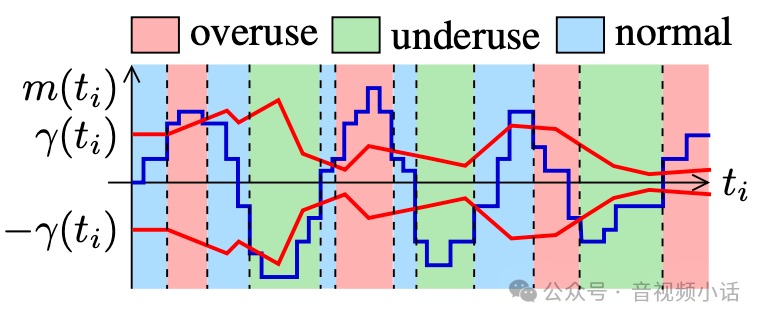
webrtc gcc详解
webrtc的gcc算法(Google Congestion Control),貌似国内很多文章都没有细讲,原理是怎么样的,具体怎么进行计算的。这里详解一下gcc。 gcc算法,主要涉及到: 拥塞控制的关键信息和公式 卡曼滤波算法 gcc如何使用卡曼滤…...

Linux多进程和多线程(七)进程间通信-信号量
进程间通信之信号量 资源竞争 多个进程竞争同一资源时,会发生资源竞争。 资源竞争会导致进程的执行出现不可预测的结果。 临界资源 不允许同时有多个进程访问的资源, 包括硬件资源 (CPU、内存、存储器以及其他外 围设备) 与软件资源(共享代码段、共享数据结构) …...
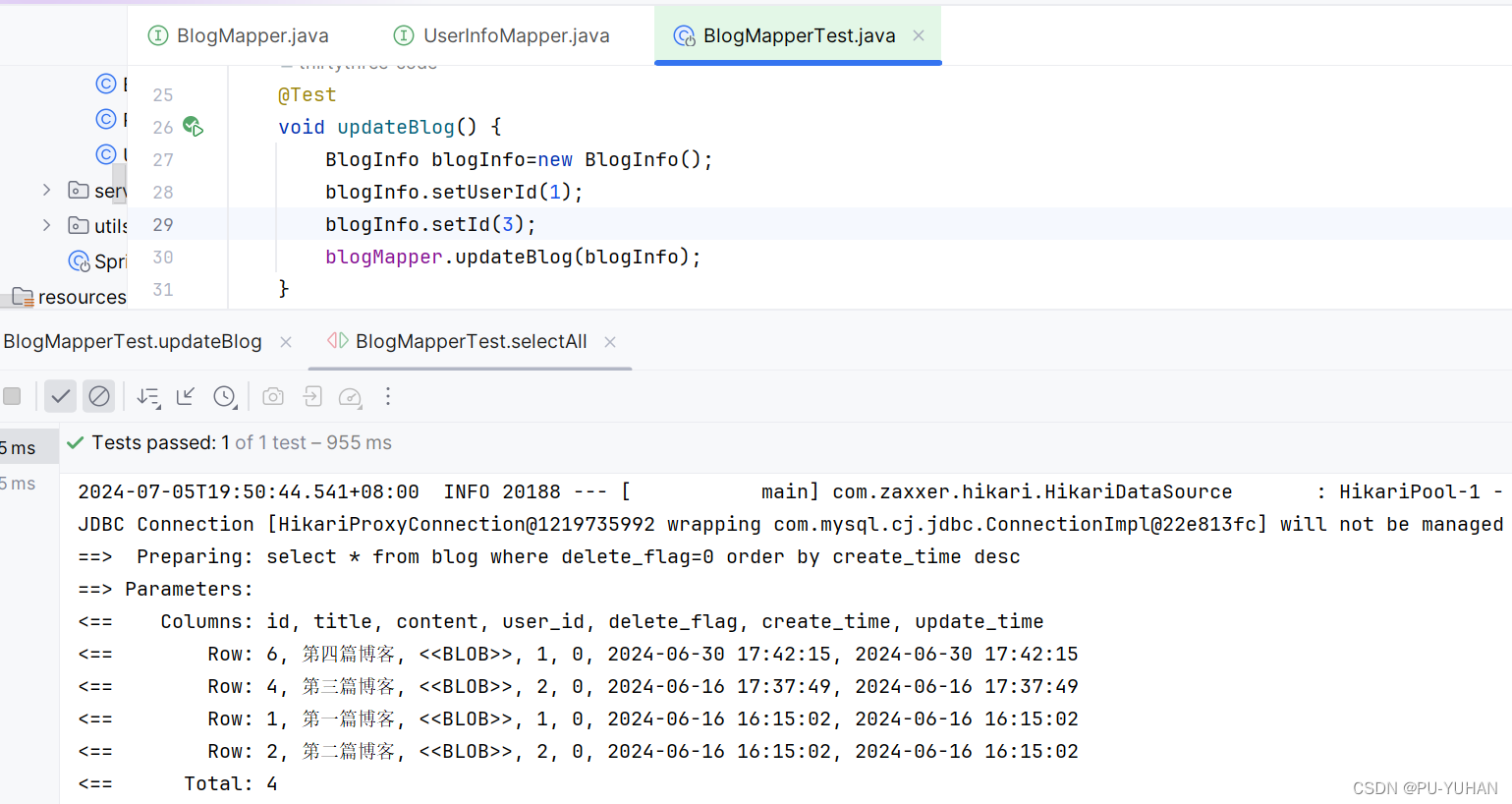
【项目日记(一)】梦幻笔耕-数据层实现
❣博主主页: 33的博客❣ ▶️文章专栏分类:项目日记◀️ 🚚我的代码仓库: 33的代码仓库🚚 🫵🫵🫵关注我带你了解更多项目内容 目录 1.前言2.后端模块3数据库设计4.mapper实现4.1UserInfoMapper4.2BlogMapper 5.总结 1.…...

ElementUI的中国省市区级联数据插件element-china-area-data
安装 npm install element-china-area-data -S import 使用 import {provinceAndCityData,pcTextArr,regionData,pcaTextArr,codeToText, } from "element-china-area-data"; provinceAndCityData省市二级联动数据,汉字+coderegionData省市区三级联动数据pcTextAr…...
Kotlin算法:把一个整数向上取值为最接近的2的幂指数值
Kotlin算法:把一个整数向上取值为最接近的2的幂指数值 import kotlin.math.ln import kotlin.math.powfun main(args: Array<String>) {val number intArrayOf(2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18)number.forEach {println("$…...

简单且循序渐进地查找软件中Bug的实用方法
“Bug”这个词常常让许多开发者感到头疼。即使是经验丰富、技术娴熟的开发人员在开发过程中也难以避免遭遇到 Bug。 软件中的故障会让程序员感到挫败。我相信在你的软件开发生涯中,也曾遇到过一些难以排查的问题。软件中的错误可能会导致项目无法按时交付。因此&…...

基于springboot+vue+uniapp的高校宿舍信息管理系统小程序
开发语言:Java框架:springbootuniappJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包&#…...

(完整音频)DockerHub、OpenAI、GitCode,脱钩时代,我们该如何自处?
本期主播 朱峰:「津津乐道播客网络」创始人,产品及技术专家。(微博:zhufengme)高春辉:「科技乱炖」主播。“中国互联网站长第一人”,科技、互联网领域的连续创业者。(微博࿱…...

macos 10.15系统下载包,macOS Catalina for mac
macOS Catalina 让你喜欢的种种 Mac 体验都更进一步。你可以领略音乐、播客这两款全新 Mac app 的表演;在 Mac 上畅享各款自己心爱的 iPad app;拿起 iPad 和 Apple Pencil,拓展工作空间,释放创意灵感;再打开那些平时常…...
 和 uni.showShareImageMenu({}) 的区别)
uni.showShareMenu({}) 和 uni.showShareImageMenu({}) 的区别
ChatGPT uni.showShareMenu({}) 和 uni.showShareImageMenu({}) 是 Uni-app 中两个不同的 API,它们的作用和用法有所不同: uni.showShareMenu({}) 作用:用于显示当前页面的分享菜单,通常显示在页面的右上角(类似于微…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...
