HTML CSS 基础复习笔记 - 列表使用
用于自己复习
自定义列表
示例代码
<!DOCTYPE html>
<html>
<head><title>Definition List Example</title>
</head>
<body><h1>古诗</h1><dl><dt>静夜思</dt><dd>床前明月光，疑是地上霜。举头望明月，低头思故乡。</dd><dt>草</dt><dd>离离原上草，一岁一枯荣。野火烧不尽，春风吹又生。</dd><dt>春晓</dt><dd>春眠不觉晓，处处闻啼鸟。夜来风雨声，花落知多少。</dd></dl>
</body>
</html>
效果：
代码简要说明
dl代表的是 Definition List，表示自定义列表
dt代表是Definition Term，表示定义（术语）标题
dd代表是Definition Description，表示定义描述
有序列表
示例代码
<!DOCTYPE html>
<html>
<head><title>Definition List Example</title><style>ol {list-style-type: decimal;list-style-position: inside;/* list-style-image: url(dove.png); */}</style>
</head>
<body><h1>古诗</h1><ol start="2" reversed type="1"><li>静夜思 - 床前明月光，疑是地上霜。举头望明月，低头思故乡。</li><li>草 - 离离原上草，一岁一枯荣。野火烧不尽，春风吹又生。</li><li value="21">春晓 - 春眠不觉晓，处处闻啼鸟。夜来风雨声，花落知多少。</li><li>登鹳雀楼 - 白日依山尽，黄河入海流。欲穷千里目，更上一层楼。</li><li>江雪 - 千山鸟飞绝，万径人踪灭。孤舟蓑笠翁，独钓寒江雪。</li></ol>˙
</body>
</html>效果
代码简要说明
ol代表order list，有序列表
li代表 list item，即每一个项
其中：ol拥有属性 start是指序号起始值，reversed是序号反转，type是指序号类型，与style中的style作用基本一致，均指序号类型，可选值为 - 1、A、a、I、i
li中的value属性，特指该项的序号为21，后面以此为起始值
样式属性中
list-style-type: decimal; 代表使用数字类型
可选值 - decimal、decimal-leading-zero、lower-roman、upper-roman、lower-alpha、upper-alpha、lower-greek、upper-latin、lower-latin、none
list-style-position: inside (或是 outside); 代表项目符号是出现在列表项内、外
无序列表
示例代码
<!DOCTYPE html>
<html>
<head><title>Definition List Example</title><style>ul {list-style-type: square;list-style-position: inside;list-style-image: url(item.jpg);}</style>
</head>
<body><h1>古诗</h1><ul><li>静夜思 - 床前明月光，疑是地上霜。举头望明月，低头思故乡。</li><li>草 - 离离原上草，一岁一枯荣。野火烧不尽，春风吹又生。</li><li>春晓 - 春眠不觉晓，处处闻啼鸟。夜来风雨声，花落知多少。</li><li>登鹳雀楼 - 白日依山尽，黄河入海流。欲穷千里目，更上一层楼。</li><li>江雪 - 千山鸟飞绝，万径人踪灭。孤舟蓑笠翁，独钓寒江雪。</li></ul>˙
</body>
</html>效果
代码简要说明
ul指的是unorder list 即无序列表，没有上述ul拥有的属性，同样，li也不具备value属性。
样式属性中
list-style-type: square; 代表项目符号使用方形
可选值 - disc、circle、square、none
list-style-position: outside / inside;
list-style-image: url(item.jpg); 代表使用图片作为项目符号
相关文章：
HTML CSS 基础复习笔记 - 列表使用
用于自己复习 自定义列表 示例代码 <!DOCTYPE html> <html> <head><title>Definition List Example</title> </head> <body><h1>古诗</h1><dl><dt>静夜思</dt><dd>床前明月光，疑…...
017-GeoGebra基础篇-微积分函数求解圆弧面积问题
基础篇慢慢的走进尾声，今天给大家带来一个小项目，是关于高中数学微积分部分的展示，这个项目主要包含了函数的介绍、函数与图形绘制的区别、区域函数图像的绘制、积分函数的应用、动态文本的调用、嵌套滑动条的应用等等，以及其他常…...
Element中的选择器组件Select （一级选择组件el-select）
简述：在 Element UI 中，ElSelect（或简称为 Select）是一个非常常用的选择器组件，它提供了丰富的功能来帮助用户从一组预定义的选项中选择一个或多个值。这里来简单记录一下 一. 组件和属性配置 <el-selectv-model&q…...
数值分析笔记（五）线性方程组解法
三角分解法 A的杜利特分解公式如下： u 1 j a 1 j ( j 1 , 2 , ⋯ , n ) , l i 1 a i 1 / u 11 ( i 2 , 3 , ⋯ , n ) , u k j a k j − ∑ m 1 k − 1 l b m u m j ⇒ a k j ( j k , k 1 , ⋯ , n ) , l i k ( a i k − ∑ m 1 k − 1 l i n u m k ) /…...
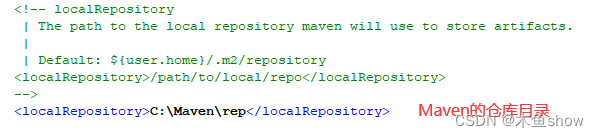
IDEA中Maven的配置
目录 1. 安装maven 2. 配置环境变量 3. IDEA中配置Maven 4. 配置仓库目录 1. 安装maven 官网下载地址：Maven – Download Apache Maven 下载后，将zip压缩包解压到某个目录即可。 2. 配置环境变量 变量名称随意，通常为M2_HOMEÿ…...
成人高考本科何时报名-深职训学校帮您规划学习之路
你有想过继续深造自己的学历吗？也许你已经工作多年，但总觉得学历是一块心病，想要通过成人高考本科来提升自己。不用着急，今天我们来聊一聊成人高考本科的报名时间，以及深职训学校如何帮助你顺利完成报名。 深圳成人高…...
)
C++ STL 协程(Coroutines)
一：什么是协程(Coroutines)： 协程是轻量级线程，可以暂停和恢复执行，协程拥有自己的暂停点状态，协程暂停时，将当前状态保存起来，在恢复执行时会恢复之前保存的状态。 二：例子： #include <coroutine> #include <iostream>void doTheWork() {std::cout <…...
虚拟机下基于海思移植QT（一）——虚拟机下安装QT
0.参考资料 1.海思Hi3516DV300 移植Qt 运行并在HDMI显示器上显示 2.搭建海思3559A-Qt4.8.7Openssl开发环境 1.报错解决 通过下面命令查询 strings /lib/x86_64-linux-gnu/libc.so.6 | grep GLIBC_通过命令行没有解决： sudo apt install libc6-dev libc6参考解决…...
计算机网络部分知识点整理
停止等待协议的窗口尺寸为 1。 √以太网标准是IEEE802.3TCP/IP四层，OSI模型有7层，地址解析协议 ARP 在 OSI 参考七层协议属于数据链路层，在TCP/IP 协议属于网络层，ARP作用：将 IP 地址映射到第二层地址，交换…...
【Qt】Qt概述
目录 一. 什么是Qt 二. Qt的优势 三. Qt的应用场景 四. Qt行业发展方向 一. 什么是Qt Qt是一个跨平台的C图形用户界面应用程序框架，为应用程序开发者提供了建立艺术级图形界面所需的所有功能。 Qt是完全面向对象的，很容易扩展，同时Qt为开发…...
读书笔记-《魔鬼经济学》
这是一本非常有意思的经济学启蒙书，作者探讨了许多问题，并通过数据找到答案。 我们先来看看作者眼中的“魔鬼经济学”是什么，再选一个贴近我们生活的例子进行阐述。 01 魔鬼经济学 中心思想：假如道德代表人类对世界运转方式的期…...
2024.7.7总结
今天是惊心动魄的一天，记录一下吧! 昨天晚上害怕早上闹铃响了听不到，担心有意外出现，错过回家的车票，于是便在晚上设置了3个闹铃，6:50，7:00，7:05然后也关了静音。没想到，早上按照正…...
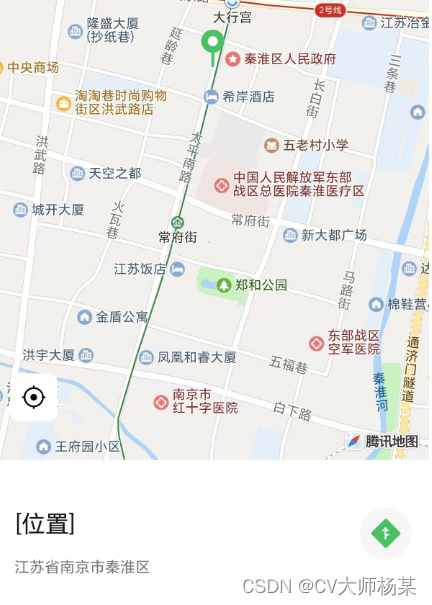
uniapp做小程序内打开地图展示位置信息
使用场景：项目中需要通过位置信息打开地图查看当前位置信息在地图那个位置，每个酒店有自己的经纬度和详细地址，点击地图按钮打开内置地图如图 方法如下： <view class"dttu" click"openMap(info.locationY,info.…...
leetcode 283.移动零
leetcode 283.移动零 自己刷题并且进行记录一下 题解 c class Solution { public:void moveZeroes(vector<int>& nums) {int count 0;for (int i 0; i < nums.size(); i) {if(nums[i] ! 0) {nums[count] nums[i];if (count !i) {nums[i] 0;}count;}}} };...
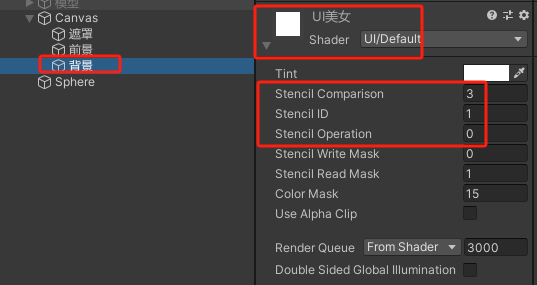
Unity | Shader基础知识(第十七集：学习Stencil并做出透视效果)
目录 一、前言 二、了解unity预制的材质 三、什么是Stencil 四、UGUI如何使用Stencil（无代码） 1.Canvas中Image使用Stencil制作透视效果 2.学习Stencil 3.分析透视效果的需求 五、模型如何使用Stencil 1.shader准备 2.渲染顺序 3.Stencil代码语…...
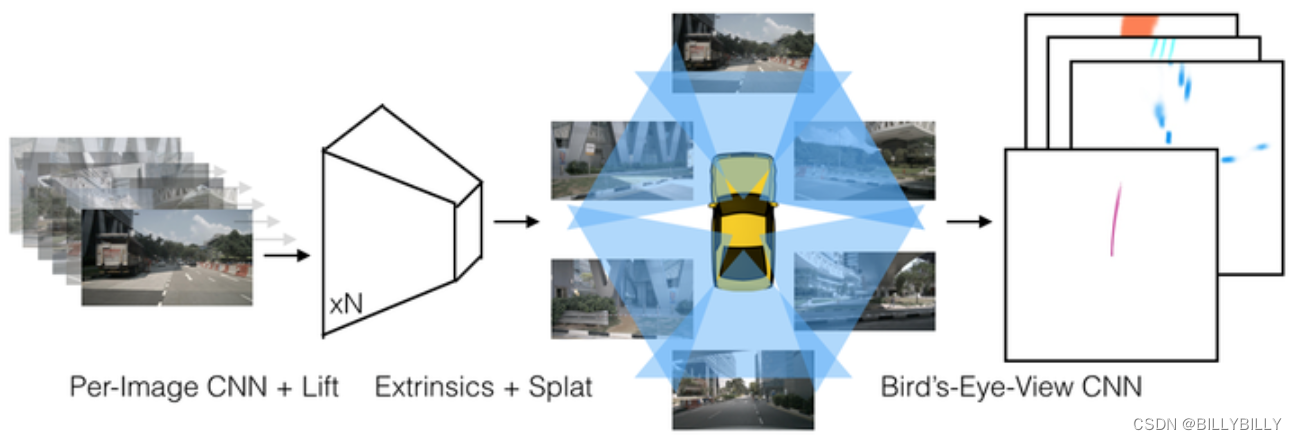
【3D-＞2D转换（1）】LSS（提升，投放，捕捉）
Lift, Splat, Shoot 这是一个端到端架构，直接从任意数量的摄像头数据提取给定图像场景的鸟瞰图表示。将每个图像分别“提升（lift）”到每个摄像头的视锥（frustum），然后将所有视锥“投放（splat&a…...
MyBatis 框架核心及面试知识要点
1、什么是 MyBatis? MyBatis 是一款优秀的支持自定义 SQL 查询、存储过程和高级映射的持久层框架，消除了 几乎所有的 JDBC 代码和参数的手动设置以及结果集的检索 。 MyBatis 可以使用 XML,或注解进 行配置和映射，MyBatis 通过将参数映射到配置的 SOL,形…...
《linux系统内核设计与实现》-实现最简单的字符设备驱动
开发linux内核驱动需要以下4个步骤： 1 编写hello驱动代码 驱动代码如下 helloDev.c，这是一个最小、最简单的驱动，去掉了其他的不相干代码，尽量让大家能了解驱动本身。 #include <linux/module.h> #include <linux/mod…...
【MotionCap】pycharm 远程在wsl2 ubuntu20.04中root的miniconda3环境
pycharm wsl2 链接到pycharmsbin 都能看到内容，/root 下内容赋予了zhangbin 所有，pycharm还是看不到/root 下内容。sudo 安装了miniconda3 引发了这些问题 由于是在 root 用户安装的miniconda3 所以安装路径在/root/miniconda3 里 这导致了环境也是root用户的，会触发告警 WA…...
[BJDCTF 2nd]简单注入
sqlsqlsqlsqlsql又来喽 过滤了单双引号，等于符号，还有select等，但是这里没有二次注入 。扫描发现hint.txt 看出题人的意思是，得到密码即可获得flag。 select * from users where username$_POST["username"] and passw…...
论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（二）
HoST框架核心实现方法详解 - 论文深度解读（第二部分） 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章： 论文深度解读 + 算法与代码分析（二） 作者机构： 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题： 人形机器人…...
逻辑回归：给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告（肿瘤大小、血液指标），你需要做出一个**决定性判断**：恶性还是良性？这种“非黑即白”的抉择，正是**逻辑回归（Logistic Regression）** 的战场&a…...
【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中，有几种方法可以执行Shell指令： 1. 使用system()函数 这是最简单的方法，包含在stdlib.h头文件中： #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...
Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...
【机器视觉】单目测距——运动结构恢复
ps：图是随便找的，为了凑个封面 前言 在前面对光流法进行进一步改进，希望将2D光流推广至3D场景流时，发现2D转3D过程中存在尺度歧义问题，需要补全摄像头拍摄图像中缺失的深度信息，否则解空间不收敛…...
基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架，支持"一次开发，多端部署"，可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务，为旅游应用带来…...
Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧！！！非常感谢！！持续更新！！！ 🚀 AI篇持续更新中！（长期更新） 目前2025年06月05日更新到： AI炼丹日志-28 - Aud…...
从零开始打造 OpenSTLinux 6.6 Yocto 系统（基于STM32CubeMX）（九）
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile，新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...
NFT模式：数字资产确权与链游经济系统构建
NFT模式：数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新：构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议：基于LayerZero协议实现以太坊、Solana等公链资产互通，通过零知…...
OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波（Mean Shift Filtering）函数meanShiftFiltering()
操作系统：ubuntu22.04 OpenCV版本：OpenCV4.9 IDE:Visual Studio Code 编程语言：C11 算法描述 在 GPU 上对图像执行 均值漂移滤波（Mean Shift Filtering），用于图像分割或平滑处理。 该函数将输入图像中的…...