二叉树的链式结构
前言
Hello,友友们,小编将继续重新开始数据结构的学习,前面讲解了堆的部分知识,今天将讲解二叉树的链式结构的部分内容。
1.概念回顾与新增
二叉树是一种数据结构,其中每个节点最多有两个子节点,分别是左子节点和右子节点。二叉树的链式结构表示是使用指针(或引用)来连接节点,形成树形结构。每个节点包含一个数据元素和两个指向子节点的指针。

2.简单创建二叉树
分为节点的定义,创建节点,创建树
下面我们将简单的手撕一个二叉树:
typedef struct BTnode {int val;struct BTnode* left;struct BTnode* right;
}Node;//节点创建
Node* BuyNode(int x) {Node* node = (Node*)malloc(sizeof(Node));if (node == NULL) {perror("node fail");return NULL;}node->val = x;node->left = NULL;node->right = NULL;return node;
}
//树的创建
Node* CreatTree() {Node* node1 = BuyNode(1);Node* node2 = BuyNode(2);Node* node3 = BuyNode(3);Node* node4 = BuyNode(4);Node* node5 = BuyNode(5);Node* node6 = BuyNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
}3.二叉树的遍历
3.1前序遍历
void PreOrder(Node* root) {if (root == NULL) {printf("N ");return;}printf("%d ", root->val);PreOrder(root->left);PreOrder(root->right);}

3.2中序遍历
void InOrder(Node* root) {if (root == NULL) {printf("N ");return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);}运行结果:N 3 N 2 N 1 N 5 N 4 N 6 N
3.3后序遍历
void PostOrder(Node* root) {if (root == NULL) {printf("N ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);}运行结果:N N 3 N 2 N N 5 N N 6 4 1
3.4层序遍历

3.4.1队列的实现
// 队列结构
typedef struct Queue {Node* data[MAX];int front;int rear;
} Queue;// 初始化队列
void initQueue(Queue* q) {q->front = 0;q->rear = 0;
}// 入队
void enqueue(Queue* q, Node* node) {if ((q->rear + 1) % MAX == q->front) {printf("Queue is full\n");return;}q->data[q->rear] = node;q->rear = (q->rear + 1) % MAX;
}// 出队
Node* dequeue(Queue* q) {if (q->front == q->rear) {printf("Queue is empty\n");return NULL;}Node* node = q->data[q->front];q->front = (q->front + 1) % MAX;return node;
}// 判断队列是否为空
int isEmpty(Queue* q) {return q->front == q->rear;
}3.4.2层序遍历实现
从根节点开始,将每个节点的值打印出来,并依次将其左子节点和右子节点加入队列。
// 层序遍历函数
void levelOrder(Node* root) {if (root == NULL) {return;}Queue q;initQueue(&q);enqueue(&q, root);while (!isEmpty(&q)) {Node* node = dequeue(&q);printf("%d ", node->val);if (node->left) {enqueue(&q, node->left);}if (node->right) {enqueue(&q, node->right);}}
}3.5主函数测试代码
int main() {Node* root = CreatTree();PreOrder(root);printf("\n");InOrder(root);printf("\n");PostOrder(root);printf("\n");levelOrder(root);return 0;
}运行结果展示:

4.遍历相关选择练习
结束语
好了,本节内容到此结束了,主要对二叉树的遍历有了新的认识理解,下一节小编将介绍二叉树的相关计算操作。最后感谢友友们的支持,动下手指给小编点点赞,发个评论吧!!!
相关文章:

二叉树的链式结构
前言 Hello,友友们,小编将继续重新开始数据结构的学习,前面讲解了堆的部分知识,今天将讲解二叉树的链式结构的部分内容。 1.概念回顾与新增 二叉树是一种数据结构,其中每个节点最多有两个子节点,分别是左子节点和右子…...

【STM32】在标准库中使用DMA
1.MDA简介 DMA全称Direct Memory Access,直接存储区访问。 DMA传输将数据从一个地址空间复制到另一个地址空间。当CPU初始化这个传输动作,传输动作本身是由DMA控制器来实现和完成的。DMA传输方式无需CPU直接控制传输,也没有中断处理方式那样保留现场和…...
多线程详解
文章目录 多线程创建方式p3一些教程 狂神说 多线程创建方式p3 代码: package com.demo1;//创建线程方式一:继承Thread类,重写run()方法,调用start开启线程/*** 总结:注意,线程开启不一定立即执行,dCPU调度执行*/public class TestThread1 extends Thre…...

软件工程需求之:业务需求与用户需求
在软件开发项目中,"业务需求"和"用户需求"是两个核心概念,它们分别从不同的角度描述了软件应该具备的功能和特性。理解这两个概念的区别对于成功地规划和开发软件至关重要。 业务需求 业务需求主要关注于软件项目如何帮助实现企业…...

Nettyの源码分析
本篇为Netty系列的最后一篇,按照惯例会简单介绍一些Netty相关核心源码。 1、Netty启动源码分析 代码就使用最初的Netty服务器案例,在bind这一行打上断点,观察启动的全过程: 由于某些方法的调用链过深,节约篇幅…...

MySQL远程登录
root是超级管理员,默认情况下,root不能作为远程登录的用户名,远程登录前,需要将登录的数据库在本地登录,修改权限,输入: update user set host % where user root ; 回车键,再输…...

html的作业
目录 作业题目 1.用户注册 A图 B代码 2.工商银行电子汇款单 A图 B代码 3.李白诗词 A图 B代码 4.豆瓣电影 A图 B代码 学习产出: 作业题目 1.用户注册 A图 B代码 <!DOCTYPE html> <html lang"zh"> <head><meta charset&qu…...

【TORCH】查看dataloader里的数据,通过dataloader.dataset或enumerate
文章目录 dataloader.dataset示例代码使用自定义数据集使用 MNIST 数据集 说明 enumerate示例代码说明使用 MNIST 数据集的例子 dataloader.dataset 是的,您可以直接访问 train_loader 的数据集来查看数据,而不必通过 enumerate 遍历数据加载器。可以通…...

KDTree 简单原理与实现
介绍 K-D树是一种二叉树的数据结构,其中每个节点代表一个k维点,可用于组织K维空间中的点,其中K通常是一个非常大的数字。二叉树结构允许对多维空间中的点进行非常有效的搜索,包括最近邻搜索和范围搜索,树中的每个非叶…...

[c++] 可变参数模版
前言 可变参数模板是C11及之后才开始使用,学校的老古董编译器不一定能用 相信大家在刚入门c/c时都接触过printf函数 int printf ( const char * format, ... ); printf用于将数据格式化输出到屏幕上,它的参数非常有意思,可以支持任意数量,任意类型的多参数.而如果我们想实现类…...

QWidget窗口抗锯齿圆角的一个实现方案(支持子控件)2
QWidget窗口抗锯齿圆角的一个实现方案(支持子控件)2 本方案使用了QGraphicsEffect,由于QGraphicsEffect对一些控件会有渲染问题,比如列表、表格等,所以暂时仅作为研究,优先其他方案 在之前的文章中&#…...

数据结构之“队列”(全方位认识)
🌹个人主页🌹:喜欢草莓熊的bear 🌹专栏🌹:数据结构 前言 上期博客介绍了” 栈 “这个数据结构,他具有先进后出的特点。本期介绍“ 队列 ”这个数据结构,他具有先进先出的特点。 目录…...
密码学复习
目录 基础 欧拉函数 欧拉函数φ(n)定义 计算方法的技巧 当a=a_1*a_2*……*a_n时 欧拉定理 剩余系 一些超简单密码 维吉尼亚 密钥fox 凯撒(直接偏移) 凯特巴氏(颠倒字母表) 摩斯密码(字母对应电荷线) 希尔(hill)密码 一些攻击 RSA 求uf+vg=1 快速幂模m^…...
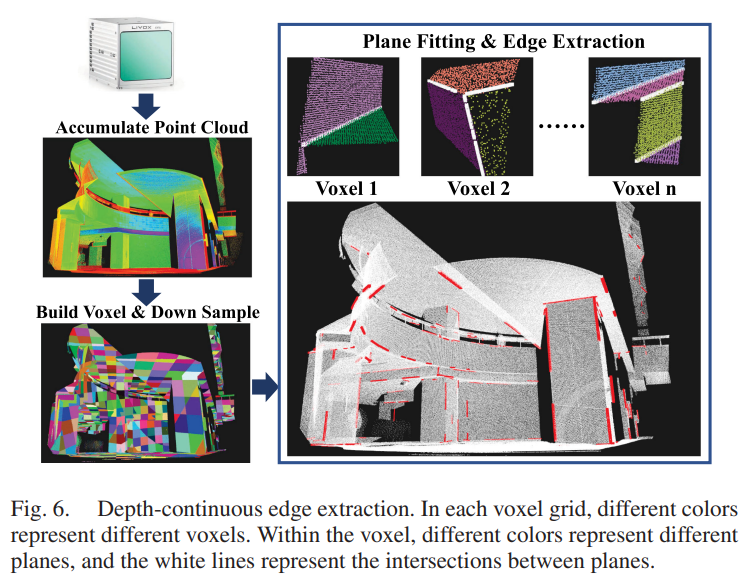
【文献解析】一种像素级的激光雷达相机配准方法
大家好呀,我是一个SLAM方向的在读博士,深知SLAM学习过程一路走来的坎坷,也十分感谢各位大佬的优质文章和源码。随着知识的越来越多,越来越细,我准备整理一个自己的激光SLAM学习笔记专栏,从0带大家快速上手激…...

Http 实现请求body体和响应body体的双向压缩方案
目录 一、前言 二、方案一(和http header不进行关联) 二、方案二(和http header进行关联) 三、 客户端支持Accept-Encoding压缩方式,服务器就一定会进行压缩吗? 四、参考 一、前言 有时请求和响应的body体比较大,需要进行压缩,以减少传输的带宽。 二、方案一(和…...

C++(Qt)-GIS开发-简易瓦片地图下载器
Qt-GIS开发-简易瓦片地图下载器 文章目录 Qt-GIS开发-简易瓦片地图下载器1、概述2、安装openssl3、实现效果4、主要代码4.1 算法函数4.2 瓦片地图下载url拼接4.3 多线程下载 5、源码地址6、参考 更多精彩内容👉个人内容分类汇总 👈👉GIS开发 …...

誉天教育7月开班计划:为梦想插上腾飞的翅膀!
随着夏日的脚步渐近,誉天教育也迎来了新一轮的学习热潮。在这个充满活力和希望的季节里,我们精心策划了7月的开班计划,旨在为广大学子提供一个优质、高效的学习平台,助力他们追逐梦想,实现自我价值。 本月 Linux云计算…...

STM32基础篇:GPIO
GPIO简介 GPIO:即General Purpose Input/Output,通用目的输入/输出。就是一种片上外设(内部模块)。 对于STM32的芯片来说,周围有一圈引脚,有时需要对引脚进行读写(读:从外部输入一…...

HTTPS 发送请求出现TLS握手失败
最近在工作中,调外部接口,发现在clientHello步骤报错,服务端没有返回serverHello。 从网上找了写方法,都没有解决; 在idea的vm options加上参数: -Djavax.net.debugSSL,handshake 把SSL和handshake的日…...

数字化精益生产系统--IFS财务管理系统
IFS财务管理系统是一款功能丰富、高效且灵活的企业财务管理软件,广泛应用于多个行业和不同规模的企业中。以下是对IFS财务管理系统的功能设计:...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

