【学习笔记】程序设计竞赛
程序设计竞赛
文章目录
- 程序设计竞赛
- 0x00 基本操作指南
- 0x01 算法分析
- 0x02 STL和基本数据结构
- 栈
- 队列
- 集合
- map
- 0x03 排序
- 插入排序
- 归并排序(Merge Sort)
- 快速排序
- 0x04 搜索技术
- BFS
- DFS
- 回溯与剪枝
- 深度迭代
- ID A*
- A star
- 双向广搜
- 0x05 递推方程
- 0x06 高级数据结构
- 并查集
- 二叉树
- 二叉搜索树
- 退化树
- Treap树(堆)
- 伸展树Splay
- 线段树
- 树状数组
- 0x07 分治法*
- 一般方法
- 求最大最小元
- 二分搜索
- 排序问题
- 选择问题
- 斯特拉森
- 0x08 动态规划(Dynamic Programming,DP)*
- 定义
- 硬币组合
- 0/1 背包问题
- 滚动数组
- 最短路径问题
- 最长公共子序列(LCS)
- 最少拦截问题 => LIS 最长递增子序列
- 矩阵连乘问题
- 0x09 基础语法
- 0x10 二分答案
- 概念
- 练习
- 整数域二分
- 实数域二分
- 0x11 贪心法(Greedy)*
- 导言
- 背包问题
- 0/1 背包问题
- 一般背包问题
- 活动安排问题
- 最佳合并模式
- 0x12 数论
- 质数
- 快速幂
- 矩阵快速幂
- 约数
- 扩欧算法
- 0x13 图论
- 基本概念
- 无向图和有向图的连通性
- 0x14 回溯法*
- 基本概念
- 涂色问题
- 4/n-皇后问题
- 0/1背包问题
- 0x15 分支限界法*
- 4-皇后问题
- 0x16 优先队列
0x00 基本操作指南
输入的结束,推荐使用下面的非~:位运算符,按位取反;只有当x值为-1时(-1的补码:11111111),~x的值才为0
while(~scanf("%d%d", &a, &b))
指定数据个数结束,提高程序编写效率
int main(){int n, a, b;scanf("%d", &n);while(n -- ){}
}
以特定元素作结束符,以读取到0结束为例
while(~scanf("%d", &n) && n)
-
测试的两种方法:
- 在程序中加入测试代码
#include<stdio.h> #define mytest int main(){int n;#ifdef mytestfreopen("test.in", "r", stdin); //将stdin重定向到test.in文件,file redirect 不需要从键盘输入了//freopen("test.out", "w", stdout); #endifwhile(~scanf("%d", &n) && n){printf("%d\n", n * n);}return 0; }- 在命令行中重定向 好处在于不需要修改源代码适合测多个文件
#include<stdio.h> int main(){int n;while(~scanf("%d", &n) && n){printf("%d\n", n * n);}return 0; }上面文件abc.cpp 一定注意要把源文件进行编译 生成exe文件
然后在相同位置 创建test.in文件 记事本
在该位置进入到当前目录 执行命令
abc < test1.in > test1.out
<: 输入>: 输出重定向把结果存入到test1.out
然后对比我们的结果和答案(答案是我们预测的结果)是否相同
fc test1.out answer.out
命令进阶版
创建xxx.bat文件 批量化执行命令脚本
abc <test1.in> test1.out abc <test2.in> test2.out abc <test3.in> test3.out fc test1.out answer1.out fc test2.out answer2.out fc test3.out answer3.out pause
提速:
- 使用STL库
- 不使用动态调试 而是通过打印中间信息
- 模板
算法证明 :
- 归纳法
- 反证法
在c++ 中引入c的函数进行提速文件头
#include<iostream>
#include<cstdio>
#include<cmath>using namespace std;int main(){return 0;
}
- 题目类型:
- Ad Hoc,杂题;
- Complete Search(Iterative/Recursive),穷举搜索
- Divide and Conquer,分治法
- Greedy,贪心法
- Dynamic Programming,动态规划
- Graph,图论
- Mathmatics,数学
- String Processing,字符串处理
- Computation Geometry,计算几何
- Some Harder,罕见问题
- 代码规范
- 少用
课本推荐的题目全部要做掉 没时间做来上课干嘛
int最大:2147483647 20多个亿
- 报错:
RE:Runtime Error 运行错误 大部分都是数组越界 特殊:除0越界
MLE:数组开太大
- 区分scanf和cin的区别
主要是在输入一个数字+一段字符时容易出错
cin cout 提速代码: 数据达到百万级 注意:如果进行了加速 scanf 和printf就必须禁用
ios::sync_with_stdio(flase);
cin.tie(0);
cout.tie(0);
- bug 避坑
如果创建副本 会导致执行相同的exe文件 所以需要修改前面的命名
- 大数据测试方法:
记事本打不开 直接死掉
使用fopen
freopen("1.in","r",stdin);
//输出
freopen("1.txt", "w", stdout);
-
数组建议从1开始 因为在搜索的时候 地图如果从0开始可能有问题
-
double 类型的数据 在读入的时候是lf 但是输出本身就是f
0x01 算法分析
- 多项式复杂度
- 指数复杂度(一般是暴力求解出现)
O ( 2 n ) < O ( n ! ) < O ( n n ) O(2^n) < O(n!) < O(n^n) O(2n)<O(n!)<O(nn)
最快的方法:打表法
只输出结果
打表法:以素数个数求解
float Sum(float list[], const int n){float tempsum = 0.0;count ++;for(int i = 0; i < n; i++){count ++;tempsum += list[i];count ++;}count ++;count ++;return tempsum;
}
确定问题的规模 根据count ++的数量 T(n) = 2 * n + 3
f ( n ) = 2 n + 3 = O ( n ) 当 n ≥ 3 时 f(n) = 2n +3 = O(n)\\ 当n\ge3时 f(n)=2n+3=O(n)当n≥3时
一点一点放
10 n 2 + 4 n + 2 当 n ≥ 2 时,原式 ≤ 10 n 2 + 5 n 当 n ≥ 5 是,上式 ≤ 10 n 2 + n 2 = 11 n 2 = > O ( n 2 ) 10n^2 + 4n +2\\ 当n\ge2时,原式\le10n^2 +5n \\ 当n\ge5是,上式\le10n^2+n^2 = 11n^2 =>O(n^2) 10n2+4n+2当n≥2时,原式≤10n2+5n当n≥5是,上式≤10n2+n2=11n2=>O(n2)
反证法
10 n 2 + 9 ≠ O ( n ) 10n^2 + 9 \neq O(n) 10n2+9=O(n)
- 矩阵乘法
for(i = 0; i < n; i++){for(j = 0; j < n; j++){c[i][j] = 0;for(k = 2; k < n; k++){xxx...xxx}}
}
O(n次方)
主方法:
理解与应用
证明不会重点考查
除法相对于其他运算会非常慢 所以一般采用移位进行做除法
增长率计算方法:https://blog.csdn.net/qq_37657182/article/details/102826437


0x02 STL和基本数据结构
- STL
Standard Template Library,C++的标准模板库,竞赛中常用的数据结构和算法可以直接调用。
容器:存放数据的,如Vector list queue stack map(映射) set(集合)
容器适配器:在别的容器的基础上加上外壳 把原有的容器的基础上做一些限制和处理 如stack queue priority_queue
关联容器:set map multiset(关键词可以重复) multimap
无序关联容器:真正使用哈希表 从c++11开始 在关联容器的前面+unordered_
通用功能:
begin() 存在数据 end() 无数据
迭代器:容器和算法之间的桥梁,可以认为是一个特殊的指针,指明数据的来源和去处
算法:如sort
函数对象:谓词,比如在排序的时候按照从大到小还是从小到大 利用函数对象进行说明
在竞赛中尽量不用vector 推荐数组 Vector为动态数组
栈
hdu 1237 自己做
队列
大量删除操作 绝对别用vector
集合
set和map 本质是红黑树 Red Black Tree
本身是有序的
1 3 5 7 9
使用必须有序
A.lower_bound(k) x>=
A.upper_bound() x >
hdu 2094
凡是选手进第一个集合
失败者进第二个集合
最终比较两个集合的差 如果差是1 产生冠军 否则没有冠军
map
关联容器 键值对 key => value 映射
hdu 2648
homework
提交解题报告 用到哪些原理 基础知识 算法 源程序
每一个程序至少5个测试数据 需要大规模测试数据 不能常规的
0x03 排序
插入排序
打扑克牌的插入方法,在部分有序的数列中不断插入新的元素
//c++
template<class Type> //把类型抽象成参数 不再依赖于具体的数据类型
void insertion_sort(Type *a, int n){Type key;for(int i = 1; i < n; i++){key = a[i];int j = i - 1;while(j >= 0 && a[j] > key){a[j + 1] = a[j];j--;}a[i + 1] = key;}
}
归并排序(Merge Sort)
快速排序
0x04 搜索技术
BFS DFS 深搜 广搜
本质就是暴力搜索,走投无路就暴搜
广搜索:一层一层拨开,先离我距离为1的 再距离我为我2的 采用队列!
BFS
宽搜:绝对不要自己手写队列
/*来存一个BFS的模板
*/
int dx[] = {1, 0, -1, 0};
int dy[] = {0, 1, 0, -1};
int vis[1005][1005]; //做标记 是否访问过
struct P{int x,y,z;
};bool BFS(int x, int y, int mid){queue<P> q;q.push({x, y, a[x][y]});while(!q.empty()){P x = q.front();q.pop();//if(a[x.x][x.y] <= mid){//如果走到头了 直接返回true if(x.x == n) return true;//没走到头 继续往下走for(int k = 0; k < 4; k++){int nx = x.x + dx[k];int ny = x.y + dy[k];//矩阵范围判断 if(nx >= 1 && ny >= 1 && nx <= n && ny <= m && vis[nx][ny] == 0 && a[nx][ny] <= mid){q.push({nx, ny, max(x.z, a[nx][ny])});vis[nx][ny] = 1; //表示访问过了 }} } }return false;
}
DFS
深搜:自己手写栈
回溯与剪枝
如果明确知道某个分支下面不可行 则不再向下走
八皇后问题:
不在一个斜线:
∣ i − j ∣ = ∣ x i − x j ∣ |i - j| = |x_i - x_j| ∣i−j∣=∣xi−xj∣
剪枝的过程中要不断check
bool check(int c, int r){ for(int i = 0; i < r; i++){if(col[i] != c && abs(i - r) != abs(col[i] - c)){} } }
深度迭代
ID A*
A star
曼哈顿启发式算法
∣ x 1 − x 2 ∣ + ∣ y 1 − y 2 ∣ |x_1 - x_2| + |y_1 - y_2| ∣x1−x2∣+∣y1−y2∣
双向广搜
0x05 递推方程
分解问题的规模,以及问题的相关性
列出递推方程进行求解问题
-
必须有一个初始条件
-
计算时的常用三种方法:
-
替换法:首先猜测递推式的解,然后使用归纳法证明,如解决汉诺塔问题
T ( n ) = { 1 n = 1 2 T ( n − 1 ) + 1 n > 1 T(n)= \begin{cases} 1 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~n=1\\ 2T(n-1) + 1~~~~~~~~n>1 \end{cases} T(n)={1 n=12T(n−1)+1 n>1void Hanoi(int n, tower x, tower y, tower z){if(n){Hanoi(n-1, x, y, z);Move(n, x, y);Hanoi(n-1, z, y, x);} } -
迭代法:针对T(n)进行推导 不带入具体数据
-
主方法:
-
递归树:把中间的节点一分为2
0x06 高级数据结构
并查集
指的是不想交的集合 disjoint
经典应用:连通子图、最小生成树Kruskal算法 最近共同祖先
实现代码:
int parent[105];// 并查集初始化
void UFset() {for (int i = 1; i <= n; i++) {parent[i] = -1;}
}int find(int i) {//update the value of tempint temp;for (temp = i; parent[temp] >= 0; temp = parent[temp]);while (temp != i) {int t = parent[i];parent[i] = temp;i = t;}return temp;
}// 合并两个集合
void merge(int a, int b) {int r1 = find(a);int r2 = find(b);int tmp = parent[r1] + parent[r2];if (parent[r1] > parent[r2]) {parent[r1] = r2;parent[r2] = tmp;} else {parent[r2] = r1;parent[r1] = tmp;}
}// Kruskal算法求最小生成树的总权值
int kruskal() {int sumWeight = 0;UFset(); // 初始化并查集for (int i = 1; i <= m; i++) {int u = edges[i].u;int v = edges[i].v;// 如果 u 和 v 不在同一个集合中,选择该边if (find(u) != find(v)) {sumWeight += edges[i].w;merge(u, v); // 合并 u 和 v 所在的集合cnt++;}// 已选择的边数达到 n-1 条时,退出循环if (cnt == n - 1) {break;}}return sumWeight;
}
二叉树
后序遍历:
先往下走 先左后右 无右向上
二叉搜索树
BST,比左孩子大,比右孩子小
红黑树是其中一种 set和map就是基于红黑树的一种
Treap树:在二叉搜索树的基础上增加了优先级
意味着成为一个树堆(大根堆、小根堆)
旋转:
void rotate(Node* &o, int d){Node *k = o -> son[d ^ 1];o
}
注意son[0] 表示左孩子
son[1] 表示右孩子
在竞赛中尽量别用平衡二叉树 太繁琐
退化树
Treap树(堆)
插入:
删除:
struct 可以视为一个类
#include <iostream>using namespace std;struct Node{int x, y;Node(int x, int y){this -> x = x;this -> y = y;}void print(){cout << x << y;}
}//或者真正用类 但是注意其他的方法都是private 所以需要先声明权限
class Node{public:int x, y;Node(int x, int y){this -> x = x;this -> y = y;}//或者:Node(int x, int y):x(x),y(y){}void print(){cout << x << y;}
}
int main(){}
伸展树Splay
不要求树是平衡的 允许把任何结点放到根上去
单旋
三点共线旋
三点不共线旋
线段树
考查较少
树状数组
往往和折半查找混合在一起用
0x07 分治法*
一般方法
分-将要求解的较大规模的问题分割成k个更小规模的子问题 注意子问题和子问题之间是独立的
合-将求解出的小规模的问题的解合并为一个更大规模问题的解,自底向上逐步求出原来问题的解
SolutionType DandC(ProblemType P){ProblemType P1, P2,..., Pk;if(Small(P)) return S(P);else{Divide(P, P1, P2, P3, ... , Pk);Return Combine(DandC(P1), DandC(P2), ... , DandC(Pk));}
}
求最大最小元
说白了就是求最大值和最小值
传统法:规模不大可以用
maxmin(float a[], int n){max = min = a[0];for(int i = 1; i < n; i++){if(max < a[i]) max = a[i];else if(min > a[i]) min = a[i];}
}
分治法:
构造树,每个子树的范围为除以二
扩展:求次最大元 次最小元
#include <iostream>
#include <climits>using namespace std;const int N = 100;
float a[N];void maxmin(int left, int right, float &max, float &second_max, float &min, float &second_min) {if (left == right) {max = a[left];second_max = INT_MIN;min = a[left];second_min = INT_MAX;} else if (left + 1 == right) {if (a[left] > a[right]) {max = a[left];second_max = a[right];min = a[right];second_min = a[left];} else {max = a[right];second_max = a[left];min = a[left];second_min = a[right];}} else {int mid = left + (right - left) / 2;float lmax, left_second_max, lmin, left_second_min;float rmax, right_second_max, rmin, right_second_min;maxmin(left, mid, lmax, left_second_max, lmin, left_second_min);maxmin(mid + 1, right, rmax, right_second_max, rmin, right_second_min);// Update maxif (lmax > rmax) {max = lmax;// Check if rmax is greater than left_second_max or notif (rmax > left_second_max) {second_max = rmax;} else {second_max = left_second_max;}} else {max = rmax;// Check if lmax is greater than right_second_max or notif (lmax > right_second_max) {second_max = lmax;} else {second_max = right_second_max;}}// Update minif (lmin < rmin) {min = lmin;// Check if rmin is less than left_second_min or notif (rmin < left_second_min) {second_min = rmin;} else {second_min = left_second_min;}} else {min = rmin;// Check if lmin is less than right_second_min or notif (lmin < right_second_min) {second_min = lmin;} else {second_min = right_second_min;}}}
}int main() {int n;cin >> n;for (int i = 0; i < n; i++) {cin >> a[i];}float max, second_max, min, second_min;maxmin(0, n - 1, max, second_max, min, second_min);cout << max << " " << second_max << endl;cout << second_min << " " << min << endl;return 0;
}
二分搜索
每次砍一半,效率较高
扩展:三分搜索
#include <iostream>using namespace std;/*
三分搜索
*/const int N = 101;
int a[N];
int n;int ternarySearch(int find){int left = 0;int right = n - 1;while(left <= right){int mid1 = left + (right - left) / 3;int mid2 = right - (right - left) / 3;//给出结果 if(a[mid1] == find){return mid1;}if(a[mid2] == find){return mid2;}//调整查找范围if(find < a[mid1]){right = mid1 - 1;} else if(find > a[mid2]){left = mid2 + 1;}//在中间 else{left = mid1 + 1;right = mid2 - 1;}}return -1;
}int main(){cin >> n; for(int i = 0; i < n; i++){cin >> a[i];}int find;cin >> find;int re = ternarySearch(find);cout << re;return 0;
}
排序问题
- 二路归并排序
两段有序序列
然后谁小把谁拉下来
//Merge- 快速排序
划分:选定一个记录作为轴值,以轴值为基准将整个序列划分为两个子序列,把比轴值小的放左边,比轴值大的放右边
左右寻找的方法:最左边放i 最右边放j 然后同时向中间缩,根据大小不断交换
void QuickSort(int a[], int p, int r){if(p < r){int q = Partition(a, p, r);QuickSort(a, p, p - 1); //对左半段排序QuickSort(a, p + 1, r); //对右半段排序}
}
int Partition(int a[], int p, int r){int i = p, j = r + 1;int x = a[p];while(ture){while(a[++i] < x);while(a[--j] > x);}
}
主元选择:
- 随机选(不做要求)
- 线性时间选择
int RandomizedSelect(int a[], int p, int r, int k){if(p == r) return a[p];int i = RandomizedPartition(a, p, r);j = i - p + 1;if(k <= j) return RandomizedSelect(a, p, i, k);else return RandomizedSelect(a, i + 1, r, k - j);
}
划分:n -> 3/4 n
五个一组进行划分 然后每组组内进行排序
1 2 3 4 5
2 3 4 5 6
. . . | . . .
. . . | . . .
. . . | . . .
这样划分后左上角一定比中间的小 右下角一定比中间的大
前面找一个大的 与后面找一个小的地方进行交换
原理:
选择一个基准元素
然后从两端向基准元素探测,直到右边的比基准元素小,左边的比基准元素大,我们进行比较,如果这两个探测的元素还是原位置,没有交界,则这两个元素互换位置。因为我们的目的就是基准元素左边的比它小,右边的比它大
当ij相遇,则交换基准元素位置和相遇位置元素
对左右分割段采用递归调用重复操作
完整代码:
#include <iostream>
using namespace std;/**
* 分治法实现快速排序
**/
int a[100005];
int n;int Partition(int l, int r){int i = l - 1;int j = r + 1;int x = i + j >> 1; //选择主元 右除 while(i < j){do{i ++;}while(a[i] < a[x]);do{j --;}while(a[j] > a[x]);if(i < j) swap(a[i], a[j]);}return j;
} void quickSort(int l, int r){if(l < r){//pos作为分隔元素 对前后进行排练 int pos = Partition(l, r);quickSort(l, pos);quickSort(pos + 1, r); }
}
//数组就从下标为0开始吧
int main(){cin >> n;for(int i = 0; i < n; i ++){cin >> a[i];} quickSort(0, n - 1);for(int i = 0; i < n; i++){cout << a[i] << " ";}return 0;
}
选择问题
选第k小
分治法思想:
一趟划分 分成两个左右子表 主元是随机选的
然后主元+左子表个数为p 如果k=p直接找到 如果k<p 则只在前面找 后面直接舍弃
注意如果k > p时 在右边找的话要找第p-k小
二次选中法确定主元
斯特拉森
0x08 动态规划(Dynamic Programming,DP)*
定义
运筹学的一个分支
与分治法的区别:
-
子问题与子问题之间有交叉,重叠子问题 只解一次 => 所以效率比较高
-
并且这个问题满足最优性原理(问题的最优解包含了子问题的最优解)
-
无后向性
满足上面三个条件,可用DP
实质就是动态的表格题, 用数组来保存结果, 就是在填dp数组的表
表格是动态的,每次都在修订
大部分是从后往前搞,把原问题转化为子问题,缩小问题规模 即自底向上
硬币组合
0/1 背包问题
特殊点在于物品无法分割 ,只能全放或者全不放,这如果使用贪心算法就可能会存在一些空间的过度浪费
从右边往左边选f(j,X) = max{f(j-1, X), f(j-1, X-wj) + pj}
两步:
dp[i][j] = max{dp[i][j-1], dp[i-wj][j-1] + vj}
构造两个二维表格进行存储数据
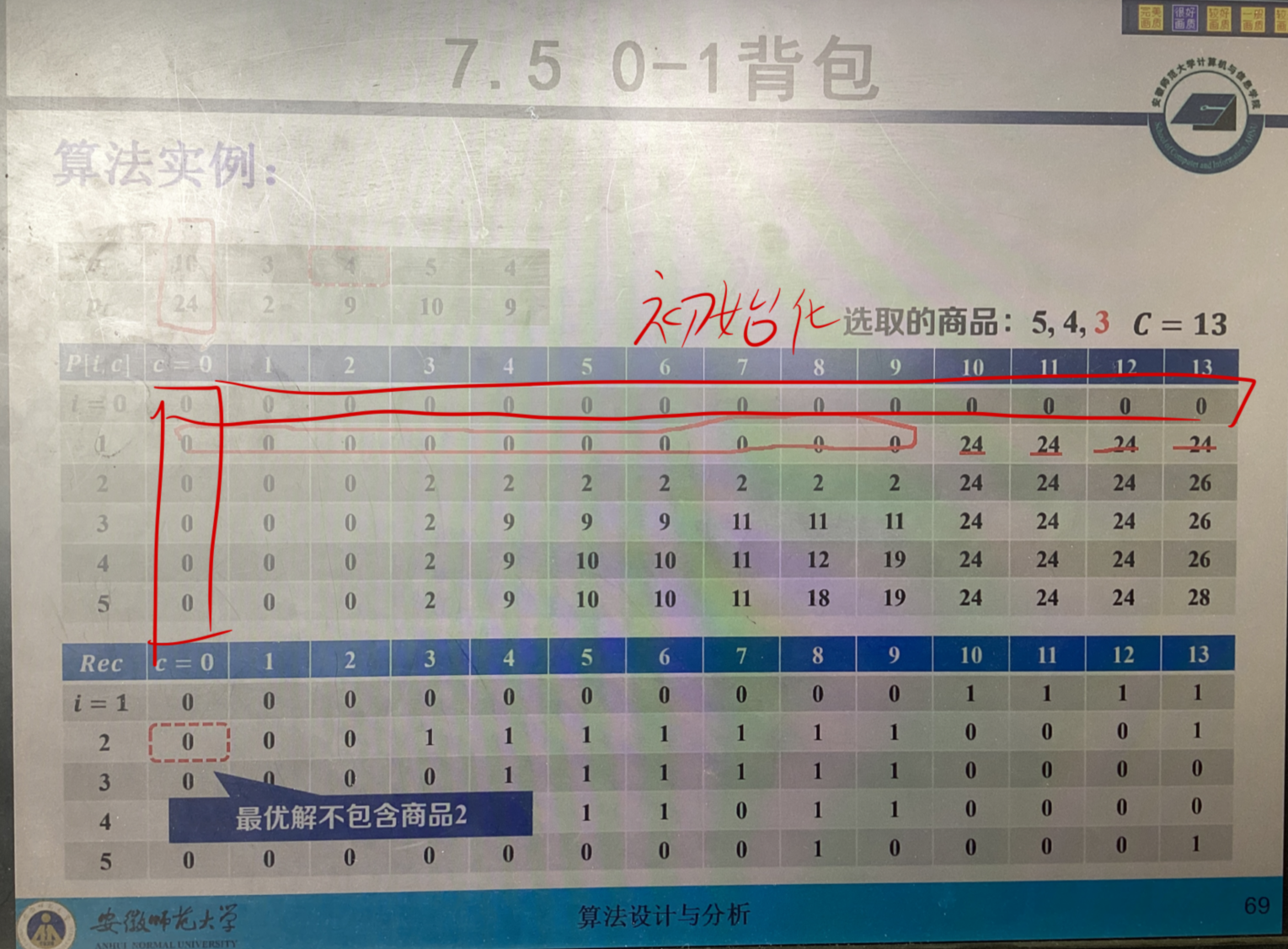
解释含义:
c 表示当背包容量为c的时候 能放入的最大价值
i 表示只选择i个的物品的情况,注意这里按顺序选择就好 比如i = 2就是计算装前两个的情况
表格数据推导:
当i = 1的时候,只判断第1个物品,c为1到9都装不下 当c=10 也就是背包容量为10的时候,可以装装下,价值为24,当背包容量继续扩大,那包装下的啊
当i = 2的时候,判断第1个和第2个物品,当c=1的时候,针对物品2列式子,有两种可能 针对上一个判断
f(2,1)= f(1, 1-3) + 2 = f(1, -2) + 2 装入
f(2,1) = f(1,1) 不装入
在f函数中第一个参数表示第几个物品,第二个参数表示背包容量情况
因为-2不符合实际要求,所以只能不装入,值为f(1,1)= 0
以此类推,当c=3时
f(2,3)=f(1, 3-3) + 2 = f(1, 0) + 2 = 2 装入
f(2,3)=f(1,3) = 0 不装入
选较大值 即为2
代码实现:
//初始化 n行 m列
for(int i = 0; i <= n; i++) f[i][0] = 0;
for(int i = 0; i <= m; i++) f[0][i] = 0;
for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){//放if(j >= w[i]){f[i][j] = max(f[i - 1][j - w[i]] + p[i], f[i - 1][j]);}//不放else{f[i][j] = f[i - 1][j];}}
}
printf("%d\n", f[n][m]);
例题:


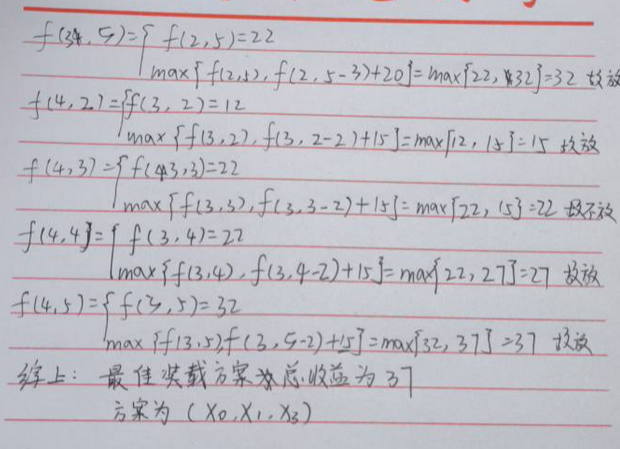
参考:https://cloud.tencent.com/developer/article/2109840
滚动数组
最短路径问题
例题:
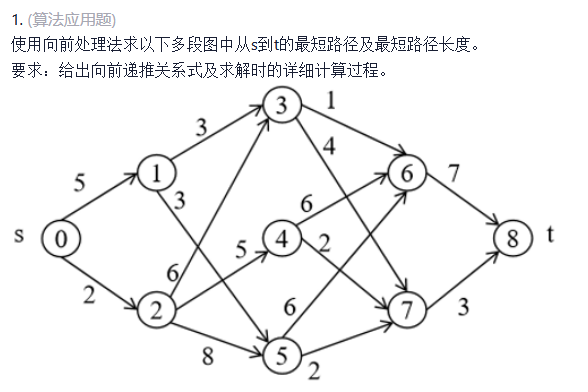
从结果往前推,一层一层进行


最长公共子序列(LCS)
实例:
X : A B C B D A B
y : B D C A B A
子序列的定义就是按照下标严格递增
考察末尾字符
如果想要进行切分,条件在于末尾字符要相同,否则去掉末尾字符可能会遗漏一些公共子序列
相等的话则一定是公共子序列啦,所以 是删除后求最优解 然后结果加上末尾相同的个数
构建过程:
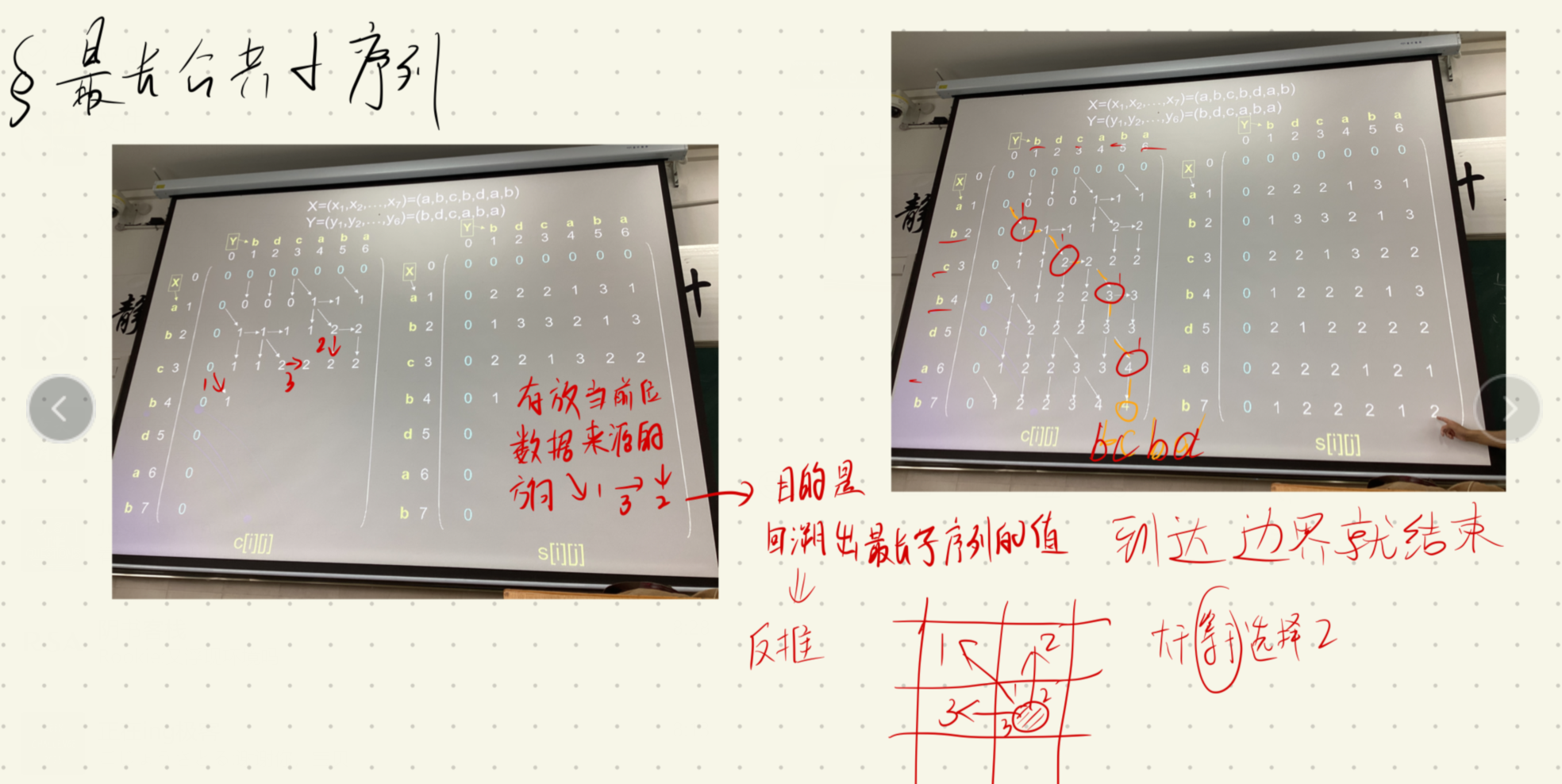
回溯代码:
void LCS(int i, int j, X, S){if(i == 0 || j == 0) return;if(S[i][j] == 1){LCS(i - 1, j - 1);cout << a[i];}else if(S[i][j] == 2) LCS(i - 1, j);else LSC(i, j - 1);
}
时间复杂度 : O(m + n)
例题:


简单来说就是如果行列的字符相同 则是左上角的值+1
如果不相同,则是左边和上面的值比较 取较大值 如果两值相等 直接数据来源于上方
参考:https://blog.csdn.net/2301_79582459/article/details/139198609
最少拦截问题 => LIS 最长递增子序列
hdu1257
举例:
3 1 5 2 4 6递增序列:
1 2 4 6 (LIS)
1 5 6
3 4 6
1 5
以3结尾:dp[0] = 1 数据长度
以1结尾:dp[1] = 1
dp[2] = 2
dp[i] = max{dp[i], dp[j]} + 1 (a[j] < a[i])
- 找出最优解的性质,并刻画其结构特征
- 递归地定义最优值
- 以自底向上
存模板:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010;
int a[N],q[N]; //a是原数组 q是需要维护的数组存储递增子序列
int n;
int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);int len = 0;for (int i = 0; i < n; i ++ ){int l = 0, r = len;//二分 不理解?? while (l < r){int mid = l + r + 1 >> 1;if (q[mid] < a[i]) l = mid;else r = mid - 1;}len = max(len, r + 1);q[r + 1] = a[i]; //不断给q插值 }printf("%d\n", len);return 0;
}
矩阵连乘问题
每行 和 每列 连乘相加 放到元素位置
乘法次数 10 * 100 100 * 5 = > 10 * 100 * 5 !是这样的
在位置k处切一道 左边最小 + 右边最小
画表 记录 在数组中
两个矩阵为4,6 6,10
次数为4 * 6 * 10
一般设置两个表
一个存放最优解的值 另一个存放如何切分才能得到最优解
设置数组
对于一系列矩阵
A i A i + 1 . . . A j m [ i ] [ j ] 表示 A i 到 A j 的最小乘法次数 A_iA_{i+1}...A_j\\ m[i][j]表示A_i到A_j的最小乘法次数 AiAi+1...Ajm[i][j]表示Ai到Aj的最小乘法次数

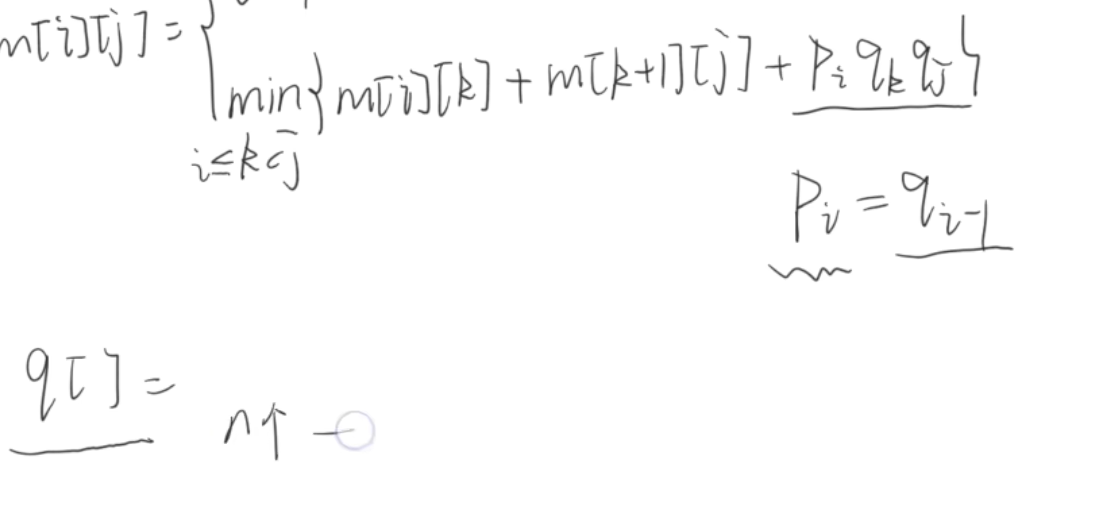
对于n个矩阵 使用q这个一维数组 n+1个元素就够了
例题:


0x09 基础语法
引用:
int a = 5;
int &x = a; //x作为a的一个引用
x = 4;
printf("%d", a); //输出是4
0x10 二分答案
概念
使用二分查找需要满足:一定要有序 单调性
识别题目:存在最大的最少 最少的最大这类字眼
#include <cstdio>
int a[1000000], n; //全局变量自动赋值为0
//如果是局部变量 记得赋值0 然后使用sum++ 这类函数 否则是随机数进行++/*** 基本二分查找实现
*/
int check(int key){int left = 0, right = n - 1, mid;while(left <= right){ //一定是小于等于mid = (left + right) >> 1; //这就是除2 其实右移和除2不是一回事 因为在正数情况下无影响 负数存在向0取整-3 右移是-2 除2是-1if(key == a[mid]) return 1;if(key > a[mid]){left = mid + 1;}else if(key < a[mid]){right = mid - 1;}}return 0; //在win下不写也能过 但是在Linux中有问题
}
例题:洛谷 P1873
看完题目一定要看一下题目范围 初步判断一下这个题目是否需要开long long
#include <bits/stdc++.h>
using namespace std;/*** 定义变量:* 1. 尽量全局* 2. 尽量见词知意*
*/
int n, m, l, r = 1e9, mid; //1e9=10的9次方
long long a[1000005], sum;int main(){scanf("%d%d", &n, &m);for(int i = 1; i <= n; i++){scanf("%lld", &a[i]);}while(l <= r){ //二分结果:1. rl位置关系 2. l = r + 1 sum = 0; //清零mid = (l + r) / 2;for(int i = 1; i <= n; i ++){if(a[i] > mid){sum += a[i] - mid;}}//可以写sum >= m 然后可以删除掉最后else的部分 因为相等时l定住不动 r一点点靠近if(sum > m){l = mid + 1;}else if(sum < m){r = mid - 1;}//仅仅这个题中符合该条件else{cout << mid;return 0;}}cout << r; //需要分析清楚return 0;
}
P1182 数列分段 SectionII
P1824 进击的奶牛
//P1824 进击的奶牛
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int n,c,a[100005];
int check(int mid){int pos=1;int k=c;while(--k){pos=lower_bound(a+1, a+n+1, a[pos]+mid)-a;if(pos==n+1) {return 0;}}return 1;
}
int main(){scanf("%d%d",&n,&c);for(int i=1; i<=n; i++) scanf("%d",&a[i]);sort(a+1, a+n+1);int l=1,r=1e9;while(l<=r){int mid=(l+r)>>1;if(check(mid)) l=mid+1;else r=mid-1; }cout<<r;return 0;
}/*
二分答案
这里二分的是奶牛之间的间隔 */
练习
课后oj例题:
A:奶茶店选址
B:野外探险
分析:
D天活动,N份干粮,N份粮食进行编号,小明从小到大开始吃 花费D天全部吃完
每份粮食能量值为Hi 每天获得能量是当天吃下的所有干粮的能量值之和 (每天吃或者不吃 吃多少都不一定)
每天的能量会在第二天开始时消耗掉一半 注意是整除的一半
设计方案,让小明获得能量值最小的那一天最大 ! 关键字眼(最小的最大)
思考:
对答案进行二分
答案的最小值是1 最大一定要设置的大一点 预测一下答案范围
解决:
每一天都要大于mid 所以不断吃 直到大于mid换下一天 看看能否正好满足天数
代码:
#include<bits/stdc++.h>using namespace std;
int N, D;
int a[50005];int check(int mid){int k = 1; //表示第几份食物 int sum[D + 5];//该函数的作用是给sum赋值为0 N个食物 D天 memset(sum, 0, sizeof(sum));//第1天灌食 因为mid是最小 所以每天获得的大于mid才能到下一天 while(sum[1] < mid && k <= N){sum[1] += a[k]; //吃能量 k++;} if(sum[1] < mid){return 0;} //第2天往后 for(int i = 2; i <= D; i++){sum[i] = sum[i - 1] / 2; //获取前一天的能量值 while(sum[i] < mid && k <= N){ //注意啊 N份食物 可以一直吃 所以有等号 要不然结果不对! sum[i] += a[k];k++; } if(sum[i] < mid){return 0;} } return 1;
}int main(){scanf("%d%d", &N, &D); for(int i = 1; i <= N ; i++){scanf("%d", &a[i]); }//需要思考 二分的是答案 对答案进行二分查找 作为最后的结果不断带进场景中做check int l = 1, r = 1e9; while(l <= r){int mid = (l + r) >> 1;if(check(mid)){l = mid + 1;} else r = mid - 1;} cout << r;return 0;
}
C:龙年邮票
分析:集邮票活动,一套完整的龙年邮票共有n种不同的造型
小明有第i种造型的邮票ai张,m张万能邮票
万能邮票可以抵任意一张,问一共能集齐多少套邮票
非常像之前支付宝的集五福啊!还有一个万能福
思考:
同样是对答案进行二分查找
代码:(有点想不到)
#include <bits/stdc++.h>using namespace std;int n, m;
int a[100];
int b[100];int check(int mid){int sum=0; //记录万能票使用数量 memcpy(b,a,sizeof b); //把a的值赋给b 对b进行操作 for(int i = 1;i <= n; i++){int x = mid - a[i]; //套数 - 当前品种数量 1 2 3 3 0 1//如果套数小于当前品种邮票数量 正常执行 检测下一个品种的邮票 if(x <= 0)continue;//如果当前品种邮票不足以支撑目标套数 则启动万能票 差x张 2 3else{for(int j = 1; j <= n; j++){if(i != j && b[j] < x) //如果存在其他品种 比当前差值还少 直接完蛋 因为万能票只能用一次 return 0;else if(i != j) //否则 对其他品种减去万能票数 b[j] -= x;}}sum += x;}if(sum <= m)return 1;return 0;}int main(){cin >> n >> m;for(int i = 1; i <= n; i++){cin >> a[i];}//把所有存在的邮票 按数量从小到大排列 sort(a + 1, a + 1 + n);int l = 1, r = 1e9;while(l <= r){int mid = (l + r) >> 1;if(check(mid)){l = mid + 1;}else{r = mid - 1;}}cout << r;return 0;
}
D : 消耗的能量
分析:n行 m列数字矩阵 第一行均为0 从第一行出发 到第n行任意位置结束
规定消耗能量为每行行走过的格子各自和的最大值
求所有路径中,小明消耗能量的最小是多少
思考:最大 最小!!! 二分答案的关键词!!!
然后涉及到路径 那么我们考虑使用bfs 去探测路径
然后在探测路径的过程中,需要去对每一行的横向进行能量探测,如果能量大于我们的二分答案值 则换下一个答案
#include <bits/stdc++.h>using namespace std;int n, m;
int a[1005][1005];/*来存一个BFS的模板
*/
int dx[] = {1, 0, -1, 0};
int dy[] = {0, 1, 0, -1};
int vis[1005][1005]; //做标记 是否访问过
struct P{int x,y,z;
};bool BFS(int x, int y, int mid){queue<P> q;q.push({x, y, a[x][y]});while(!q.empty()){P x = q.front();q.pop();//if(a[x.x][x.y] <= mid){//如果走到头了 直接返回true if(x.x == n) return true;//没走到头 继续往下走for(int k = 0; k < 4; k++){int nx = x.x + dx[k];int ny = x.y + dy[k];//矩阵范围判断 if(nx >= 1 && ny >= 1 && nx <= n && ny <= m && vis[nx][ny] == 0 && a[nx][ny] <= mid){q.push({nx, ny, max(x.z, a[nx][ny])});vis[nx][ny] = 1; //表示访问过了 }} } }return false;
}
int check(int mid){ memset(vis, 0, sizeof vis); //对vis数组 全部赋值 为0 表示没有访问过bool ans = false;for(int i = 1; i <= m; i++){ans = ans || BFS(2, i, mid); //第1行是初始行 全部为0 所以从第2行开始BFS } return ans;
}
int main(){cin >> n >> m;for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){cin >> a[i][j];}}int l = 1, r = 1005;while(l <= r){int mid = (l + r) >> 1;if(!check(mid)){ //思考一下返回的是什么 不要光想着套模板!! l = mid + 1;}else{r = mid - 1;}}cout << l;return 0;
}
整数域二分
洛谷 P1577 切绳子
有一个问题就是如果答案结果是1.99
与2.00进行相减判断 但是不通过 因为二进制表示的问题,0.1无法用二进制精确表示,所以在二进制相减中可能存在问题
Specual Judge问题,不用太在意格式 因为最终的评判标准时是与标准值作差 然后进行评判的 一般说保留三位 但是要考虑精度问题 尽量保留5位
转换方法:将小数转化到整数 先扩大 后结果缩小
实数域二分
P1570 KC 喝咖啡
P1678 烦恼的高考志愿
0x11 贪心法(Greedy)*
导言
找零问题:
每一步的判断是当前的最优选择,但是需要思考局部最优能否达到全局最优的问题
局部最优代替整体最优,其最终结果近似最优解
有点像背包问题啊
给个例子:
xi = {1, 5, 10, 20, 50, 100}
y = ∑ w i x i \sum w_ix_i ∑wixi
求min ∑ w i \sum w_i ∑wi
可行解:问题给定一些约束条件,可以满足
最优解:
通过分步决策的方法,每一步决策产生一个向量
流程:
- 存在可能解的集合
背包问题
0/1 背包问题
物体不能分割 只有两种状态 装入或者不装
一般背包问题
物体可分割,可以把物体x的xi部分装入到背包中
贪心思路:
- 价值最大
- 重量最轻
- 单位重量价值最大
方案一:按物体价值降序装包
方案二:按物品重量非降序装包
方案三:按物体价值与重量比值的降序装包 先装最大的
活动安排问题
按结束的时间进行排列
最佳合并模式
类似于哈夫曼树
0x12 数论
质数
快速幂
( a b ) m o d n (a^b) ~mod~ n (ab) mod n
快速幂就是解决上述问题
算法的思想是:分治
区分一下分治和二分的区别:
二分是舍弃掉一半,而分治是不断划分 然后合而治之
模板:
递归代码:
int quickPow(int a, int b){if(b == 1) return a;if(b % 2 == 0){int t = quickPow(a, b/2);return t * t % mod;}else{int t = quickPow(a, b/2);t = t * t % mod;t = t * a % mod;return t;}
}
非递归代码1:
int quickPow(int a, int b){int t =
}
补充:
while(b){b = b / 2;
}
该式的时间复杂度为log n 级别的
例题:P1226
例题2:
数列求值
矩阵快速幂
单位矩阵:主对角线上的元素都是1
void matrixMulti(){for(int i = 1; i <= m; i++){for(int)}
}
最关键的地方:
不是矩阵乘幂的计算,而是如何得到一个可以用来形成乘幂计算的矩阵
S n = 1 ∗ S n − 1 + 1 ∗ f n + 0 ∗ f n − 1 f n + 1 = 0 ∗ S n − 1 + 1 ∗ f n + 1 ∗ f n − 1 f n = 0 ∗ S n − 1 + 1 ∗ f n + 0 ∗ f n − 1 S_n=1*S_{n-1}+1*f_n+0*f_{n-1}\\ f_{n+1}=0*S_{n-1}+1*f_n+1*f_{n-1}\\ f_n=0*S_{n-1}+1*f_n+0*f_{n-1} Sn=1∗Sn−1+1∗fn+0∗fn−1fn+1=0∗Sn−1+1∗fn+1∗fn−1fn=0∗Sn−1+1∗fn+0∗fn−1
约数
求N的正约数集合:
- 试除法
- 倍数法
最大公约数和最小公倍数 P1029
扩欧算法
贝祖定理(斐蜀定理)
0x13 图论
基本概念
无向图和有向图的连通性
割点:去掉这个点之后 剩下的图不连通 那么这个点就是割点
割边:
双连通问题:
0x14 回溯法*
基本概念
需要找出问题的最优解 在一定的约束下进行,使用回溯法
设置一个目标函数,用来衡量每一个可能解的情况
搜索:
- 以深度优先方式搜索解空间
- 在搜索过程中使用剪枝函数,避免无效搜索
常用剪枝函数: 舍得!不行的就放弃 别挣扎
- 用约束函数在扩展结点处减去不满足约束的子树 (不满足不可行)
- 用限界函数剪去得不到最优解的字数 (可行但不最优)
涂色问题
前提:
- 不是优化问题,没有限界函数
- 搜索策略:深度优先
- 约束条件:相邻结点,不同颜色
4/n-皇后问题
解向量 :
( x 1 , x 2 , . . . , x n ) (x_1,x_2,...,x_n) (x1,x2,...,xn)
注意这个写法 直接限制了每一行只能放一个
设置约束条件:
限制列:i != j
限制对角线:
程序:
bool Place(int k, int i, int* ){for()
}
0/1背包问题
0x15 分支限界法*
4-皇后问题
广度优先
//结构体模板
template <class T>
struct Node{T cost;Node* parent;
}Node<int> t; //创建结构体 意味着上面模板中的T为int
注意上下界问题
0x16 优先队列
相关文章:

【学习笔记】程序设计竞赛
程序设计竞赛 文章目录 程序设计竞赛0x00 基本操作指南0x01 算法分析0x02 STL和基本数据结构栈队列集合map 0x03 排序插入排序归并排序(Merge Sort)快速排序 0x04 搜索技术BFSDFS回溯与剪枝 深度迭代ID A*A star双向广搜 0x05 递推方程0x06 高级数据结构并查集二叉树…...

11-云服务器处理单细胞转录组数据
目录 安装R及相关包 安装 shiny 进行安装包 安装BiocManager 安装Seurat包 网页端Rstudio需打开8787端口 Ubuntu上安装R包linux库缺失 关于服务器配置及相关处理可见:linux学习笔记_hx2024的博客-CSDN博客 安装R及相关包 8-阿里云服务器 ECS配置R及Studio Server-CS…...

vs+qt5.0 使用poppler-qt5 操作库获取pdf所有文本输出到txt操作
先获取poppler库,编译出lib与dll,配置好依赖环境,获取某页所有文本: QList<QString> PDFkitEngine::GetText(int nPageNum) { QList<QString> lstText; Poppler::Page* pPage NULL; pPage GetPage(nPageNu…...

[AIGC] ClickHouse分布式表与本地表的区别及如何查询所有本地表记录
在大规模数据处理和分析场景中,ClickHouse是一种高性能的列式数据库管理系统。ClickHouse支持分布式表和本地表两种表类型,本文将介绍这两种表类型的区别,并探讨如何建表以查询所有本地表的记录。 文章目录 一、ClickHouse分布式表与本地表的…...

202406 CCF-GESP Python 四级试题及详细答案注释
202406 CCF-GESP Python 四级试题及详细答案注释 1 单选题(每题 2 分,共 30 分)第 1 题 小杨父母带他到某培训机构给他报名参加CCF组织的GESP认证考试的第1级,那他可以选择的认证语言有几种?( ) A. 1 B. 2 C. 3 D. 4答案:C解析:目前CCF组织的GESP认证考试有C++、Pyth…...
—— 使用门控残差和变量选择网络进行分类)
政安晨:【Keras机器学习示例演绎】(五十二)—— 使用门控残差和变量选择网络进行分类
目录 简介 数据集 安装准备 数据准备 定义数据集元数据 创建用于训练和评估的 tf.data.Dataset 创建模型输入 对输入特征进行编码 实施门控线性单元 实施门控余留网络 实施变量选择网络 创建门控残差和变量选择网络模型 编译、训练和评估模型 政安晨的个人主页:政…...

Spring AOP、Spring MVC工作原理、发展演变、常用注解
Spring AOP 概念 AOP全称为Aspect Oriented Programming,表示面向切面编程。切面指的是将那些与业务无关,但业务模块都需要使用的功能封装起来的技术。 AOP基本术语 **连接点(Joinpoint):**连接点就是被拦截到的程序执…...

grid布局下的展开/收缩过渡效果【vue/已验证可正常运行】
代码来自GPT4o:国内官方直连GPT4o <template><div class"container"><button class"butns" click"toggleShowMore">{{ showAll ? 收回 : 显示更多 }}</button><transition-group name"slide-fade&…...

Qt/C++编写地图应用/离线地图下载/路径规划/轨迹回放/海量点/坐标转换
一、前言说明 这个地图组件写了很多年了,最初设计的比较粗糙,最开始只是为了满足项目需要,并没有考虑太多拓展性,比如最初都是按照百度地图写死在代码中,经过这几年大量的现场实际应用,以及大量的用户提出…...

最新版Python安装教程
一、安装Python 1.下载Python 访问Python官网: https:/www.oython.orgl 点击downloads按钮,在下拉框中选择系统类型(windows/Mac OS./Linux等) 选择下载最新稳定版本的Python 以下内容以演示安装Windows操作系统64位的python 左边是稳定发布版本Stabl…...

1.3镜像管理
【必知必会】了解镜像的命名及导入导出镜像 1.3.1镜像的命名 一般情况下,镜像是按照如下格式命名的 服务器ip:端口/分类/镜像名:tag 如果不指明端口,默认是80,tag是latest,比如:192.168.26.101:5000,再比如hub.c.163.com/library/mysql:latest.分类也可以不写,比如d…...
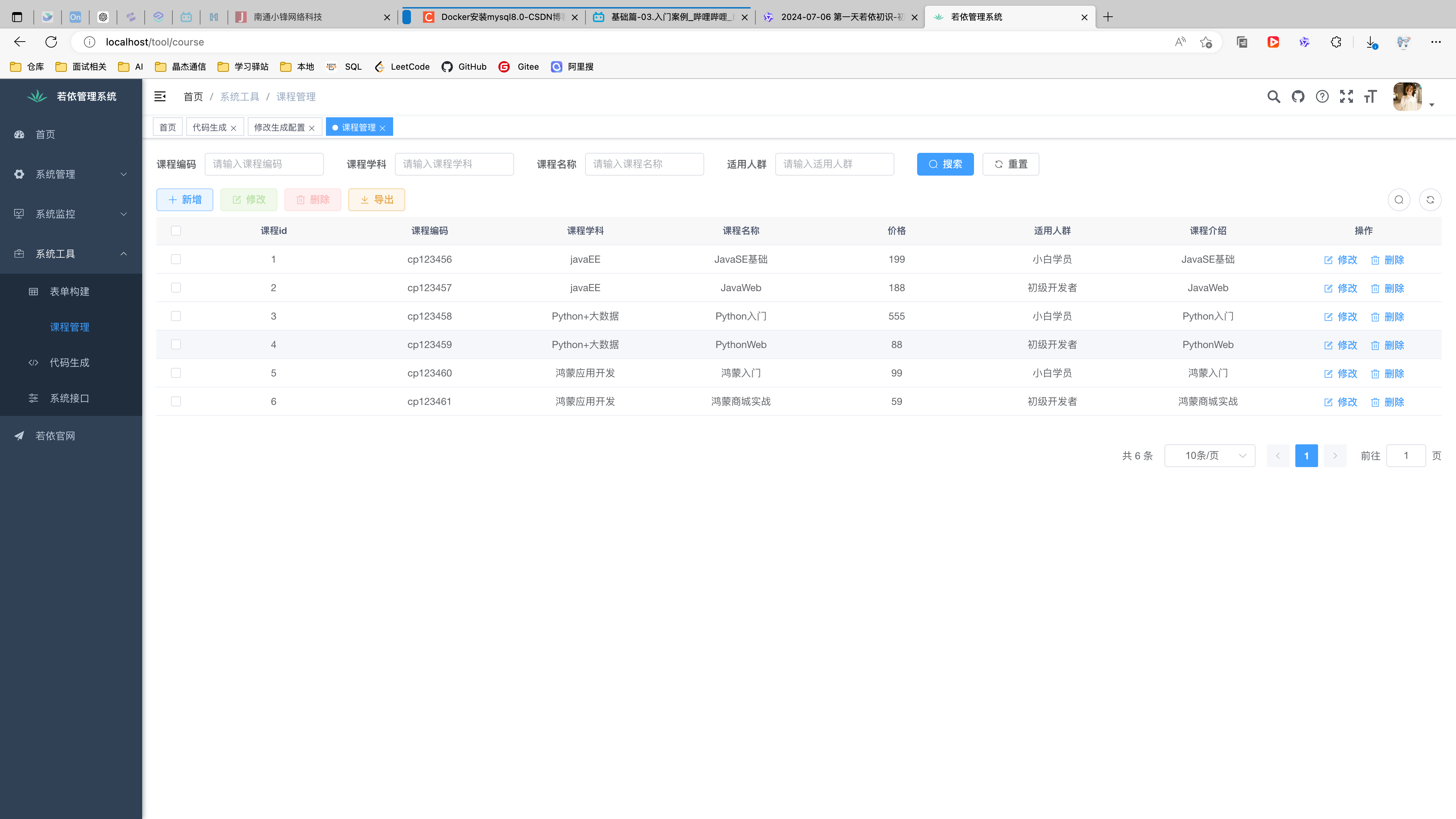
黑马|最新AI+若依 |初识项目
本章主要内容是: 1.快速搭建了若依前后端项目在本地 2.实现了单表的增删改查快速生成 文章目录 介绍1.若依介绍2.若依的不同版本3.项目运行环境 初始化前后端项目1.下载若依项目2.初始化后端a.把表导入到数据库中b.更改application.yml文件 3.初始化前端a.安装依赖…...

ArrayList综合案例-模拟外卖中的商家系统
一案例要求: 二代码要求: package 重修;import java.util.ArrayList; import java.util.Random; import java.util.Scanner;import static java.lang.System.exit;public class first {public static void main(String[] args) {Scanner scnew Scanne…...

Postgres JSON字段怎么修改key的名称
场景 当你不小心将 key 的名称写错了(人员类别:多了一个冒号),或者想把引文改为中文(type改为类型) 大致思路是添加一个新的 key,然后将旧的 key 删除 sql语句 假如 JSON 列为 extra&#x…...

GStreamer学习5----probe数据探测
参考资料: gstreamer中如何使用probe(探针)获取帧数据_gstreamer 视频编码时获取视频关键帧信息-CSDN博客 Gstreamer中可以使用AppSink作为一个分支来查看管线中的数据,还可以使用probe去处理。 在GStreamer中,probe…...

Open3D 点云的圆柱形邻域搜索
目录 一、概述 1.1原理 1.2应用 二、代码实现 2.1完整代码 2.2程序说明 三、实现效果 3.1原始点云 3.2搜索后点云 一、概述 1.1原理 圆柱邻域搜索的基本思想是确定点云中的哪些点位于给定圆柱的内部。一个圆柱可以由以下几个参数定义: 中心点:…...
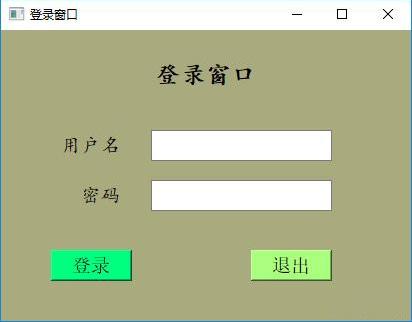
python如何设计窗口
PyQt是一个基于Qt的接口包,可以直接拖拽控件设计UI界面,下面我简单介绍一下这个包的安装和使用,感兴趣的朋友可以自己尝试一下: 1、首先,安装PyQt模块,这个直接在cmd窗口输入命令“pip install pyqt5”就行…...

C语言获取当前时间
一共有两段代码,一个是获取当前时间,一个是获取到现在的总毫秒数 求关注😄 互粉必回 获取当前时间 #include <stdio.h> #include <time.h> int main() { time_t rawtime; struct tm * timeinfo; char buffer[20]; // 获取当前…...

【每日一练】python三目运算符的用法
""" 三目运算符与基础运算的对比 """ a 1 b 2#1.基础if运算判断写法: if a > b:print("基础判断输出:a大于b") else:print("基础判断输出: a不大于b")#2.三目运算法判断:…...
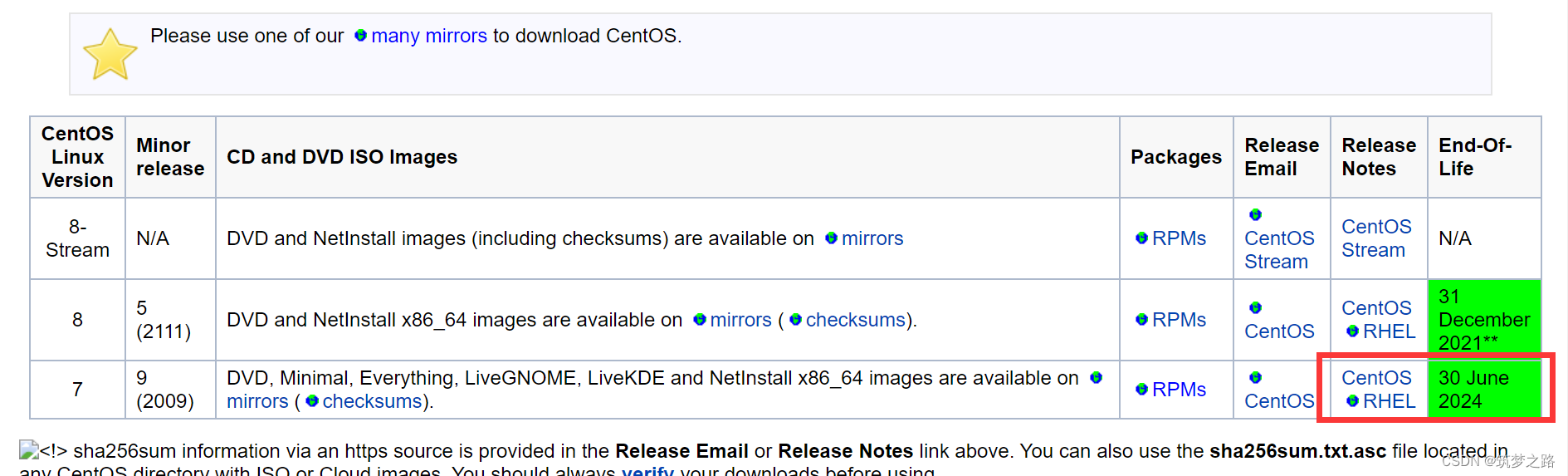
CentOS 7.9 停止维护(2024-6-30)后可用在线yum源 —— 筑梦之路
众所周知,centos 7 在2024年6月30日,生命周期结束,官方不再进行支持维护,而很多环境一时之间无法完全更新替换操作系统,因此对于yum源还是需要的,特别是对于互联网环境来说,在线yum源使用方便很…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
