秋招突击——7/4——复习{}——新作{最长公共子序列、编辑距离、买股票最佳时机、跳跃游戏}
文章目录
- 引言
- 复习
- 新作
- 1143-最长公共子序列
- 个人实现
- 参考实现
- 编辑距离
- 个人实现
- 参考实现
- 贪心——买股票的最佳时机
- 个人实现
- 参考实现
- 贪心——55-跳跃游戏
- 个人实现
- 参考做法
- 总结
引言
-
昨天主要是面试,然后剩下的时间都是用来对面试中不会的东西进行查漏补缺,顺便和同学聚会。今天继续把算法做了。
-
总觉得自己的进度还是太慢了,项目不整理出来,连简历都没有办法修改,这里得加快一下进度,然后今天除了刷算法,主要是干两件事
- 整理想去参加的暑期openday,记录在表格中
- 继续准备项目,并且根据项目完善自己的简历。
-
动态规划基本上已经全部做完了,今天能够最后几题收个尾,练了那么久,基本上都能够做出来。
复习
新作
1143-最长公共子序列
题目链接
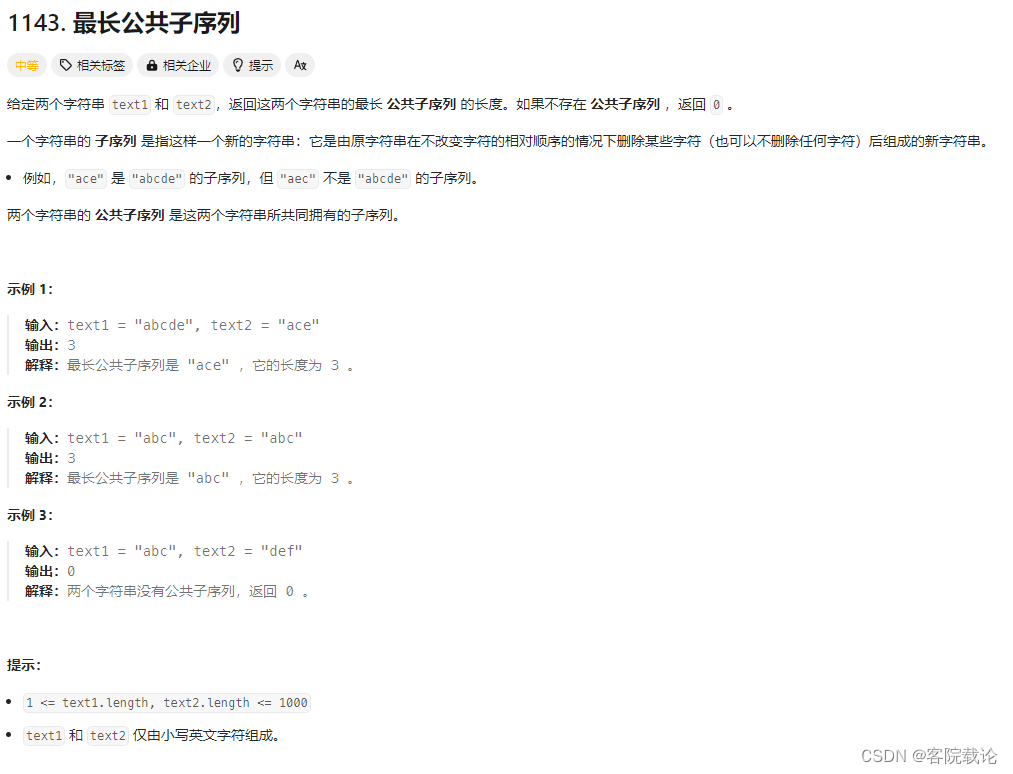
注意
- 都是小写英文字母组成==》可以使用ACSCII码进行操作
- 字符串的长度从1到1000==》注意边界条件
- 子序列==》不改变原始序列中字符相对位置的情况下,删除一部分的元素
- abcde==》ade
- 返回最长公共子序列的长度,没有返回零
个人实现
-
这道题不在之前任何一个模板里面,没什么思路,只能自己使用集合的角度去考虑问题,想想看。
-
单纯使用暴力搜索的算法是怎么做的?
- 如何提取出一个字符串的子串?每一个字符存在两种情况,加入或者不加入,假设有n个字符,那就是的2的n次方个字串了,这个问题规模太大了。何况是两个字符串
- 假设能够将两个字符串的所有子串都提取出来,那么再一个一个匹配,就是 2 n 2^n 2n * 2 n 2^n 2n,然后在比较获取最长的长度,这样问题规模就已经爆炸了。
-
在转换一下,最长的子串,肯定是建立在较短的字符子串上面的
- 任何一个字符串新增加一个字母,都有可能会改变的最终匹配的字符串的长度
- 如何从短的字符串过渡到长的字符串?使用什么方法?或者表达式?两个字符串,是不是需要从两个维度进行考虑f[i][j],分别表示的两个字符串对应到对应索引的位置,然后最长的公共子串长度?但是有一个问题,就是你需要记录的是匹配的字符串长度的索引,然后一旦后续有变化,在往后面的索引继续增加就行了。
具体推导,看是看图吧,如下图,是我自己的推导

- 整理出来了,但是没有使用集合的角度去分析,但是大概的逻辑是对的就行了,先做着吧。时间复杂度就是m*n
class Solution {
public:int longestCommonSubsequence(string t1, string t2) {int m = t1 n = t2;vector<vector<int>> f(t1,f(t2,0));vector<vector<int>> td1(t1,f(t2,0));vector<vector<int>> td2(t1,f(t2,0));// 遍历对应的索引位置for(int i = 0;i < m;i ++){for(int j = 0;j < n;j ++){// 多种情况,分别是仅仅增加i、仅仅增加j或者两者同时增加if(i) f[i][j] = max(f[i][j],f[i-1][j]+commonSeq(t1.substr(td1[i - 1][j],i),t2.substr(td2[i - 1][j],j)))if(j) f[i][j] = max(f[i][j],f[i][j-1]+commonSeq(t1.substr(td1[i][j-1],i),t2.substr(td2[i][j-1],j)))if(i && j) f[i][j] = max(f[i][j],f[i-1][j-1]+commonSeq(t1.substr(td1[i-1][j-1],i),t2.substr(td2[i-1][j-1],j)))// 还需要更新最后两者索引相同的最后的索引,方便下次调用。// 这里得更新两次,不过还是能做的,如果能够写完,还是对的。}}}
};
总结
- 整理思路加上画图,以及最后的写代码,差不多用了半个小时,还是没写完,不过严格按照时间限定出发,没做出来,不过我觉得我的思路大体还是对的。
- 有一个问题
- 单独增加一个和单独增加多个,没有任何意义,因为能够增加多个,就是表示两个数组都没有遍历完,所以还是有问题的。
思路有问题,实现不了
参考实现
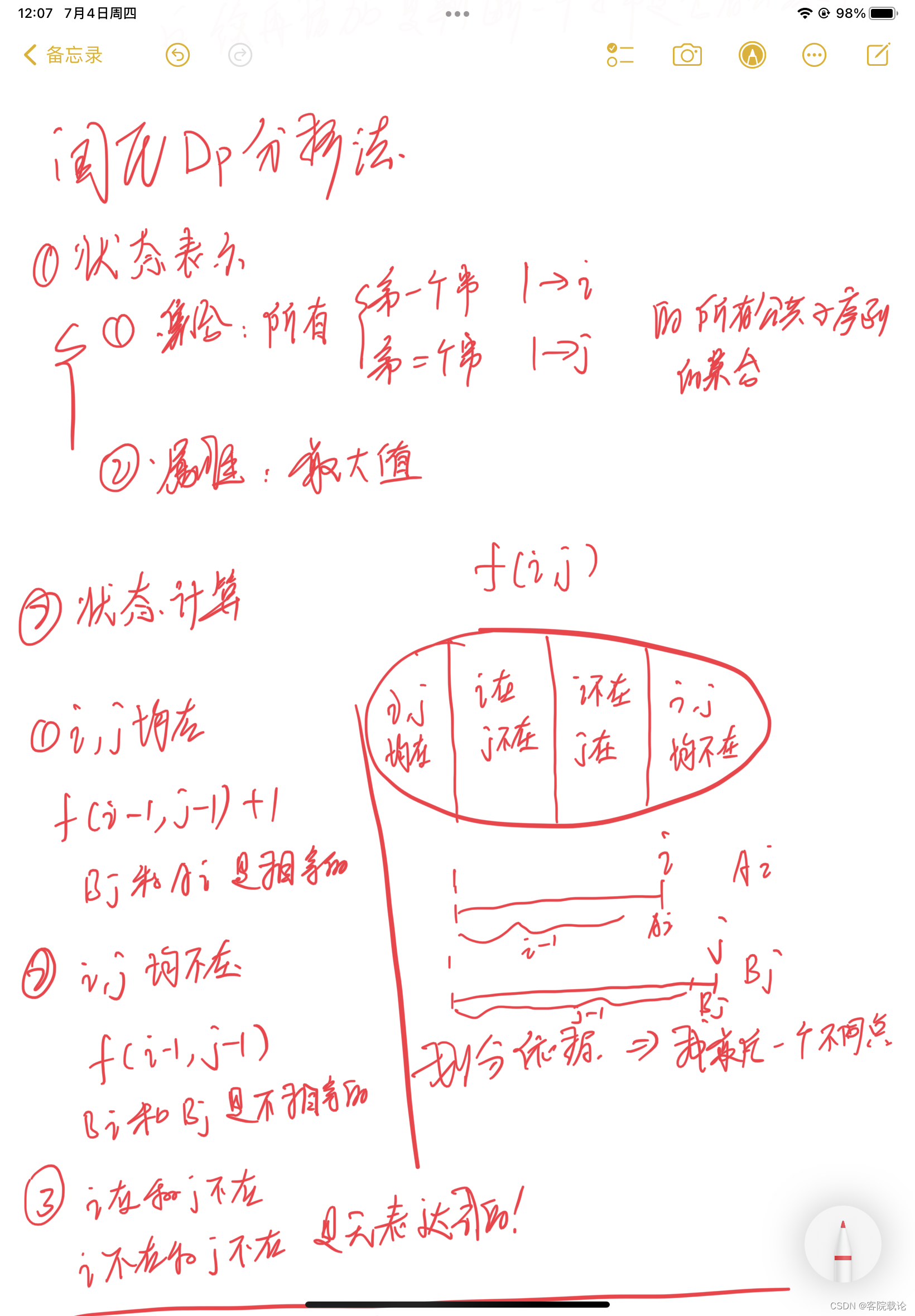

- 思路和我分析的还是比较相似的,只不过我有一个问题,就是没有意识到如果相同就加一,不同就不变,然后任何一个状态都是从最初的状态一步一步迭代过来,就像我之前的推理一一样,最基础的这个问题的形态我没有搞清楚。
- 状态当成主要有两个作用
- f[i][j] = f[i - 1][j - 1] + 1这个是表示对应的相同的迭代情况。
- 其余的不变就是, 是为了把状态不断延续下去,这个原理有的时候并不好想,也比较难想,我就是这里没有想出来,确实是一个问题。
疑难解答
- 之前还是有一个问题,就是如何保证,A列表加入一个新元素之后,另外一个列表不增加新的元素,然后新增加的元素会带来更多公共子串
- 不用担心,这里正常每一个字符串都会相互匹配一次,下一次两者 相同的时候,一定会加上这个情况
- 对于那种单个边相加的,只需要考虑上一个状态是怎么计算的就行了。
下面是我参考他的思路写的代码
class Solution {
public:int longestCommonSubsequence(string t1, string t2) {int m = t1.size(), n = t2.size();vector<vector<int>> f(m + 1,vector<int>( n + 1,0));t1 = " " + t1;t2 = " " + t2;// 遍历对应的索引位置for(int i = 1;i <= m;i ++){for(int j = 1;j <= n;j ++){// 这里是单边相加if(t1[i] != t2[j]) f[i][j] = max(f[i][j-1],f[i-1][j]);else f[i][j] = f[i - 1][j - 1] + 1;}}return f[m][n];}
};
- 这里并不知道如何处理索引为0的情况,所以这里在开头增加了一个空格
再参考修改
- 这里使用i- 1来判定是否相等就可,很聪明,跟之前个优先队列的提前试探一样。
class Solution {
public:int longestCommonSubsequence(string t1, string t2) {int m = t1.size(), n = t2.size();vector<vector<int>> f(m + 1,vector<int>( n + 1,0));// 遍历对应的索引位置for(int i = 1;i <= m;i ++){for(int j = 1;j <= n;j ++){// 这里是单边相加f[i][j] = max(f[i][j-1],f[i-1][j]);if(t1[i- 1] == t2[j - 1]) f[i][j] = f[i - 1][j - 1] + 1; }}return f[m][n];}
};
下面再leetcode上摘抄的一部分矩阵关系变化图很有参考意义
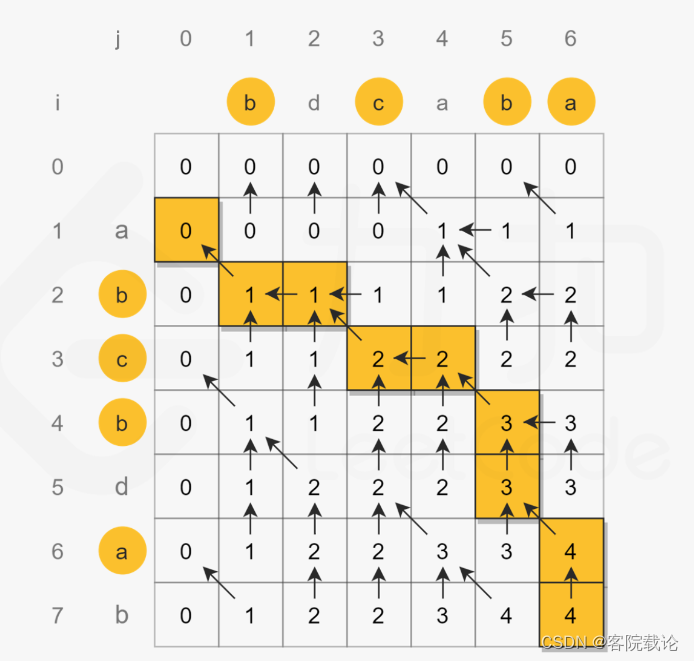
编辑距离
- 题目链接


注意
- 只有三种操作
- 插入一个新的字符==》任何位置插入元素
- 删除原来的字符==》删除任何位置的元素
- 替换对应的字符
- 将一个单词变成另外一个单词的最小操作次数
个人实现
-
首先,如果对这道题的状态限定一下,保证每一个操作之后都有固定的三种操作,就变成一个三叉树,然后进行广度优先遍历深度,是可以解决问题的,但是现在是不限定的每一层的节点数或者分支数,这个是完全没有办法的使用类似的方法。
-
首先,我们先来看看最多操作,也没有一个通用的算法,因为单词的长度的不一样。
- 目标长度单词小于当前的单词,那就先删除,保证长度是一致的,然后在替换,这个是最直接的。
- 目标长度单词大于当前的单词,那就先添加,保证的长度一致的,然后再替换,结果最直接。
-
上述方法很好实现,除此之外,我还需要确定一件事,就是删除元素之后,是否能够保证后续的元素会自动跟上,如果是的话,那么这个问题就变了,删除特定位置的元素,也能够实现单词转换。
-
动态规划,没什么思路,甚至集合都不知道怎么操作,属性表达式倒是很好说明
- f[i][j],把字符串从i变成j,所有的方案各自的步骤数量
- 属性是最小的步骤数
- 状态转换不知道了,不过和上面那道题有点像
下面的方法纯属胡扯了,没有任何必要
class Solution {
public:int minDistance(string a, string b) {int m = a.size(),n = b.size();vector<vector<int>> f(m +1 ,vector<int>(n + 1,0));for(int i =1;i <= m; i++){for(int j = 1;j <= n;j ++){if(a[i-1] == a[j-1])// 相同的话,删除中间所有的元素if(i != j) f[i][j] = f[i - 1][j - 1] + abs(i - j);else// 不同直接删除f[i][j] = f[i][j] = f[i - 1][j - 1] + 1;}}return f[m][n];}
};
忽然间有思路了,想起来了
- 计算最长公共子串的数量len,具有如下的等式关系
- 如果tar == len,直接返回sour - tar
- 如果tar > len,
- sour > tar
- sour < tar
- 如果tar < len,
- sour > tar
- sour < tar
上述几种情况需要好好理理,应该是能够解决这个问题的,但是今天又超过时间了,直接看解答。
参考实现
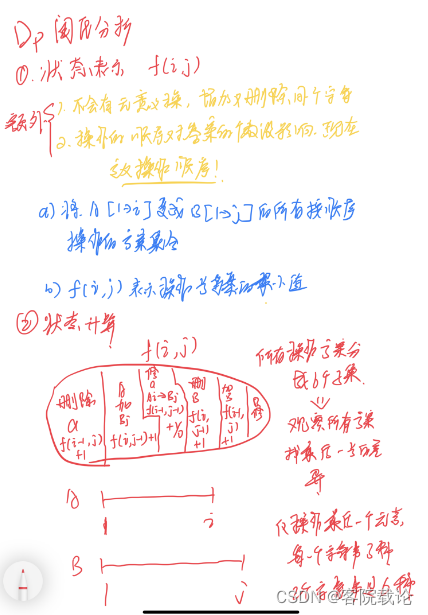

- 这道题就是属于完全想的不对,但是这种双类型的字符串的,都有一个诀窍,就是两个维度,并且都是从最后的一个元素开始考虑的,而且之前的所有元素,都是已经满足条件的,不要有额外的特殊情况。
- 这里就是假设除了最后一个元素都是匹配的,所以要对最后一个元素进行讨论和考虑,按照顺序执行三种操作即可
- 删除最后一个元素,就能保证两个字符串匹配,所以被删除的字符串的前面的所有字符串都是匹配的,f[i][j] = f[i - 1][j] + 1
- 增加一个新的元素,就能保证最后两个字符串是匹配的,并且添加地元素就是目标的最后一个元素,Bj,所以状态转移就是f[i][j] = f[i ][j- 1] + 1
- 替换掉对应的元素,两个元素都不相等
- 两个元素相等,无操作
实现代码
class Solution {
public:int minDistance(string a, string b) {int m = a.size(),n = b.size();vector<vector<int>> f(m +1 ,vector<int>(n + 1,INT_MAX));a = " " + a;b = " " + b;// 初始化边界条件for(int i = 0;i <= m;i ++) f[i][0] = i; // 目标字符串是空的,删除操作若干次for(int i = 1;i <= n;i ++) f[0][i] = i; // 当前字符串是空的,目标字符串的是有长度的,添加若干次for(int i =1;i <= m; i++){for(int j = 1;j <= n;j ++){f[i][j] = min(f[i-1][j],f[i][j-1]) + 1;int t = a[i] != b[j];f[i][j] =min(f[i][j], f[i - 1][j - 1] + t);}}return f[m][n];}
};
总结
- 为什么总是写不出来,我觉得是因为我看问题的角度和他的不一样,他的问题角度是最后一个元素就能保证当前状态完全成立,但是我会被困在中间状态,改变不了,还是改变一下。
- 这里的边界条件处理也很特殊,需要根据实际情况尽心处理。
贪心——买股票的最佳时机
题目链接


注意
- 计算能够获取的最大利润
- 当天买入,然后后续的某一天卖出,计算差价
个人实现
- 这道题就是爽题,单纯是一道状态机模型,是DP,爽题。
class Solution {
public:int maxProfit(vector<int>& prices) {vector<int> buy(prices.size() + 1,-1e6); // 持有状态:vector<int> sell(prices.size() + 1,-1e6); // 无持有状态buy[0] = 0 - prices[0];sell[0] = 0;for(int i = 1;i < prices.size();i ++){buy[i] = max(sell[i -1] - prices[i],buy[i-1]);sell[i] = max(sell[i - 1],buy[i - 1] + prices[i]);}return sell[prices.size()-1];}
};
给我整麻了,看错题了,这里是只能买入一次,然后卖出一次,不是可以操作多次
- 只能操作一次,那么直接暴力搜索就行了,平方的时间复杂度,会超时,在想想哈.
弄成下面这样,惨不忍睹
class Solution {
public:int maxProfit(vector<int>& prices) {int res = 0;vector<pair<int,int>> f(prices.size());for(int i = 0;i < prices.size();i++) {if(i + 1 < prices.size() && prices[i] == prices[i + 1]) continue;f.push_back({prices[i],i});}sort(f.begin(),f.end(),[](auto a,auto b){return a.first > b.first;});for(int i = 0;i < prices.size();i ++){if(i + 1 < prices.size() && prices[i] == prices[i + 1]) continue;// 找到往后小的元素for(auto x : f) if(x.second > i ) {res = max(res,x.first - prices[i]);break;} }return res;}
};
参考实现
- 这个思路感觉很清晰,但是我没有想到,感觉就是差点,
- 找到对于第i天的历史最低点,然后计算利润即可。遍历一次是可以记录历史最低点的,然后反复计算对应的利润就行了
class Solution {
public:int maxProfit(vector<int>& prices) {int minPrice = INT_MAX,maxPrift = 0;for(int i = 0;i < prices.size();i ++){if(prices[i] < minPrice) minPrice = prices[i];else{maxPrift = max(maxPrift,prices[i] - minPrice);}}return maxPrift;}
};
贪心——55-跳跃游戏
题目链接

注意
- 一开始位于第一个下标
- 数组的值表示你最多可以跳的次数,你可以选择[0,value]的任意一个数值作为你跳的步骤
- 数组长度边界值为一,可以跳过
- 每一个值可以为零,最大没有越界
个人实现
- 从当前的位置出发能不能到达目标点,直接使用暴力进行搜索可以试试看,遍历所有情况,如果能够找到目标点,就返回true
- 时间复杂度:最多是 1 0 9 10^9 109,应该会超时,但是可以进行剪枝,先写出来再说
- 使用dfs递归实现,具体实现如下
十五分钟写成这样,超时,只能通过一半的样例,不行
class Solution {
public:bool dfs(vector<int> nums,int idx){// 等于目标值,直接返回if(idx == nums.size() - 1) return true;for(int i = nums[idx];i >= 1;i --){if(idx + i < nums.size() && dfs(nums,idx + i)) return true; }return false;}bool canJump(vector<int>& nums) {if(nums.size() == 1) return true;if(nums[0] == 0 ) return false;// 正常情况,第一个数值不为零,并且长度超过了一return dfs(nums,0);}
};
可以将问题拆解一下,先拆成到中间某一个节点的情况
是不是思路有问题,不应该使用模拟的方式。发现了,特殊情况时针对0而言的,只要有一个非零的数字,就能够一直往下走,所以按照零进行分段就行。
class Solution {
public:// 递归调用bool dfs(vector<int> nums,int idx){// 等于目标值,直接返回if(idx == nums.size() - 1) return true;for(int i = nums[idx];i >= 1;i --){if(idx + i < nums.size() && dfs(nums,idx + i)) return true; }return false;}bool canJump(vector<int>& nums) {if(nums.size() == 1) return true;if(nums[0] == 0 ) return false;int dis = 0,sp = 0;for(int i = 0;i < nums.size() -1;i ++){if(nums[i] != 0) dis = max(dis,nums[i]);else{cout<<i<<sp<<endl;if(i - sp > dis) { return dfs(nums,i - 1);} else sp = i;}}return true;}
};
写的这个还是有问题,不伦不类的,将两个都结合了,还有问题,不过我发现,判断还是有问题的,其实不需要看整个,只需要看,零前面的那个数字是多少就行了,能不能盖过零。综合来判定,我的思路没考虑到,时间不够,认输

参考做法
- 这里跟我的思路很想,但是我没有考虑地很周全,是计算每一个点所能够访问的最远距离,如果i超过了能够访问的最远距离,就表示访问不到,直接跳过。
- 最远距离更新方式
- 判定当前的i是否可以访问到
- j = max(i + nums[i],j);
很直观的做法,没考虑到
class Solution {
public:bool canJump(vector<int>& nums) {for(int i = 0,j = 0;i < nums.size();i ++){// i超过了最远距离,不能访问了if(i > j) return false;// 没有超过最远距离,需要进行更新j = max(i + nums[i],j);}return true;}
};
总结
- 今天的进度有点慢了,为什么会这么慢,上午就刷了两道题,是因为什么?中间洗了一下衣服,然后刷了一会视频,不行,还是有点来不及。下午吃饭快点,多留点时间。
- 真的难呀,一天天的,不如开机重启!
- 难受呀,晚上两道题,没有一道题是按时AC的,那道简单题还看错题目了,然后花了很多时间,结果简答的思路都没有考虑到。不过无所谓了,学到了,练习到了,今天又刷了四道题,明天继续加油!
相关文章:

秋招突击——7/4——复习{}——新作{最长公共子序列、编辑距离、买股票最佳时机、跳跃游戏}
文章目录 引言复习新作1143-最长公共子序列个人实现 参考实现编辑距离个人实现参考实现 贪心——买股票的最佳时机个人实现参考实现 贪心——55-跳跃游戏个人实现参考做法 总结 引言 昨天主要是面试,然后剩下的时间都是用来对面试中不会的东西进行查漏补缺ÿ…...
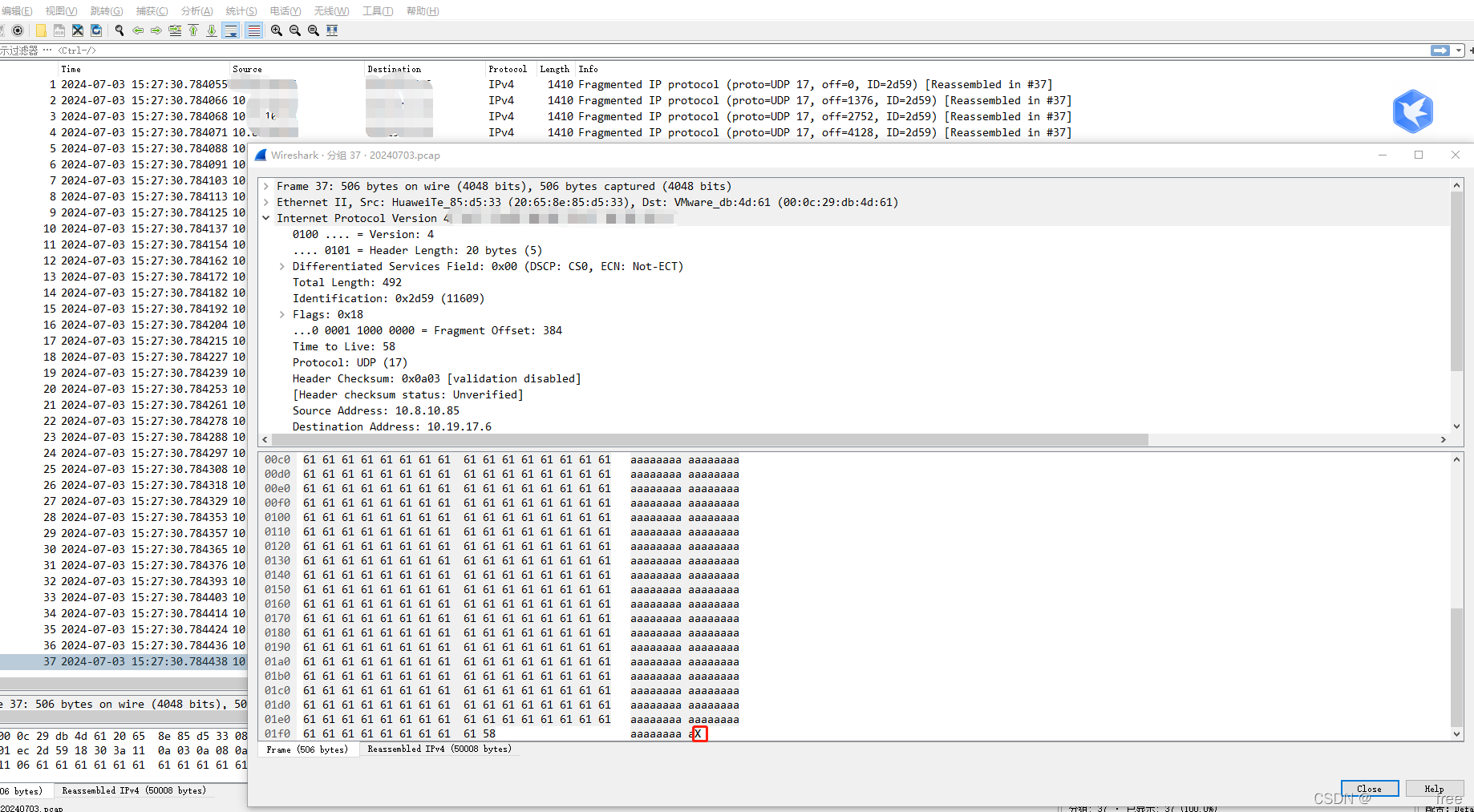
udp发送数据如果超过1个mtu时,抓包所遇到的问题记录说明
最近在测试Syslog udp发送相关功能,测试环境是centos udp头部的数据长度是2个字节,最大传输长度理论上是65535,除去头部这些字节,可以大概的说是64k。 写了一个超过64k的数据(随便用了一个7w字节的buffer)发送demo,打…...

电子电气架构 --- 智能座舱万物互联
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明自己,无利益不试图说服别人,是精神上的节…...

笔记本电脑内存不够
笔记本电脑内存不够是众多笔记本用户面临的常见问题,尤其是对于一些需要处理大型文件或者运行复杂软件的用户,这个问题可能会严重影响笔记本的使用体验。那么,我们应该如何解决笔记本电脑内存不够的问题呢?本文将从几个方面进行详…...

Vue项目使用mockjs模拟后端接口
文章目录 操作步骤1. 安装 mockjs 和 vite-plugin-mock2. 安装 axios3. 创建mock路径4. 配置 viteMockConfig5. 编写第一个mock接口6. 创建 createProdMockServer7. 配置 axios8. 编写请求接口9. 在页面中使用 操作步骤 1. 安装 mockjs 和 vite-plugin-mock vite-plugin-mock …...

Linux下使用arping检测IP地址是否冲突
arping简介 在Linux中,arping是一个用来发送ARP请求到一个相邻主机的工具,通常用于检测网络上的IP地址冲突。 使用arping检测IP地址是否冲突的方法 例1:使用如下命令检测10.206.216.95是否冲突 (使用-I参数指定网络接口) # arping -I eth…...

为什么 npm run serve 正常,npm run build 就报错:digital envelope routines::unsupported
这个错误通常与 Node.js 版本和使用的加密算法有关。让我解释一下原因和可能的解决方案: 错误原因 这个错误(“error:0308010C:digital envelope routines::unsupported”)通常发生在以下情况: 使用较新版本的 Node.js…...

模电基础 - 简介
目录 零 .简介 一. 学习方法 二. 教材推荐 三. 总结 零 .简介 “模电”即模拟电子技术,是电子信息工程、电气工程及其自动化等相关专业的一门关键基础课程。 首先,在半导体器件方面,二极管是一种具有单向导电性的器件,由 P 型…...

uniapp中实现瀑布流 短视频页面展示
直接上干货 第一部分为结构 <swiper class"list" :currentindex change"swiperchange" scrolltolower"onReachBottom"><swiper-item style"overflow: scroll;" v-for"(item,index) in 2" :key"index"&g…...
python-开关灯(赛氪OJ)
[题目描述] 假设有 N 盏灯(N 为不大于 5000 的正整数),从 1 到到 N 按顺序依次编号,初始时全部处于开启状态;第一个人( 1 号)将灯全部关闭,第二个人( 2 号)将…...
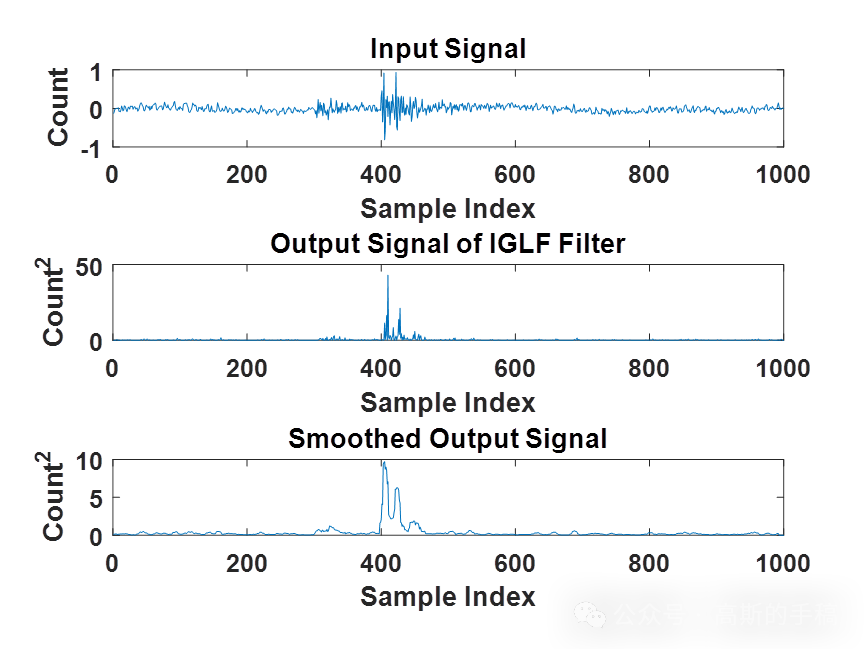
基于改进高斯-拉普拉斯滤波器的一维时间序列平滑与降噪(MATLAB)
以图像处理为例,拉普拉斯算子是基于图像的二阶导数来找到边缘并搜索过零点,传统的拉普拉斯算子常产生双像素宽的边缘,对于较暗区域中的亮斑进行边缘检测时,拉普拉斯运算就会使其变得更亮。因此,与梯度算子一样…...

计算组的妙用!!页面权限控制
需求描述: 某些特殊的场景下,针对某页看板,需要进行数据权限卡控,但是又不能对全部的数据进行RLS处理,这种情况下可以利用计算组来解决这个需求。 实际场景 事实表包含产品维度和销售维度 两个维度属于同一公司下面的…...

Self-Instruct构造Prompt的例子
人工构造一批Prompt做种子。(Starting with a small seed set of human-written tasks)每次把一些种子后来生成的Prompt,放到Input里做few-shot examples,用LLM生成更多的Prompt;(Using the LLM to generat…...
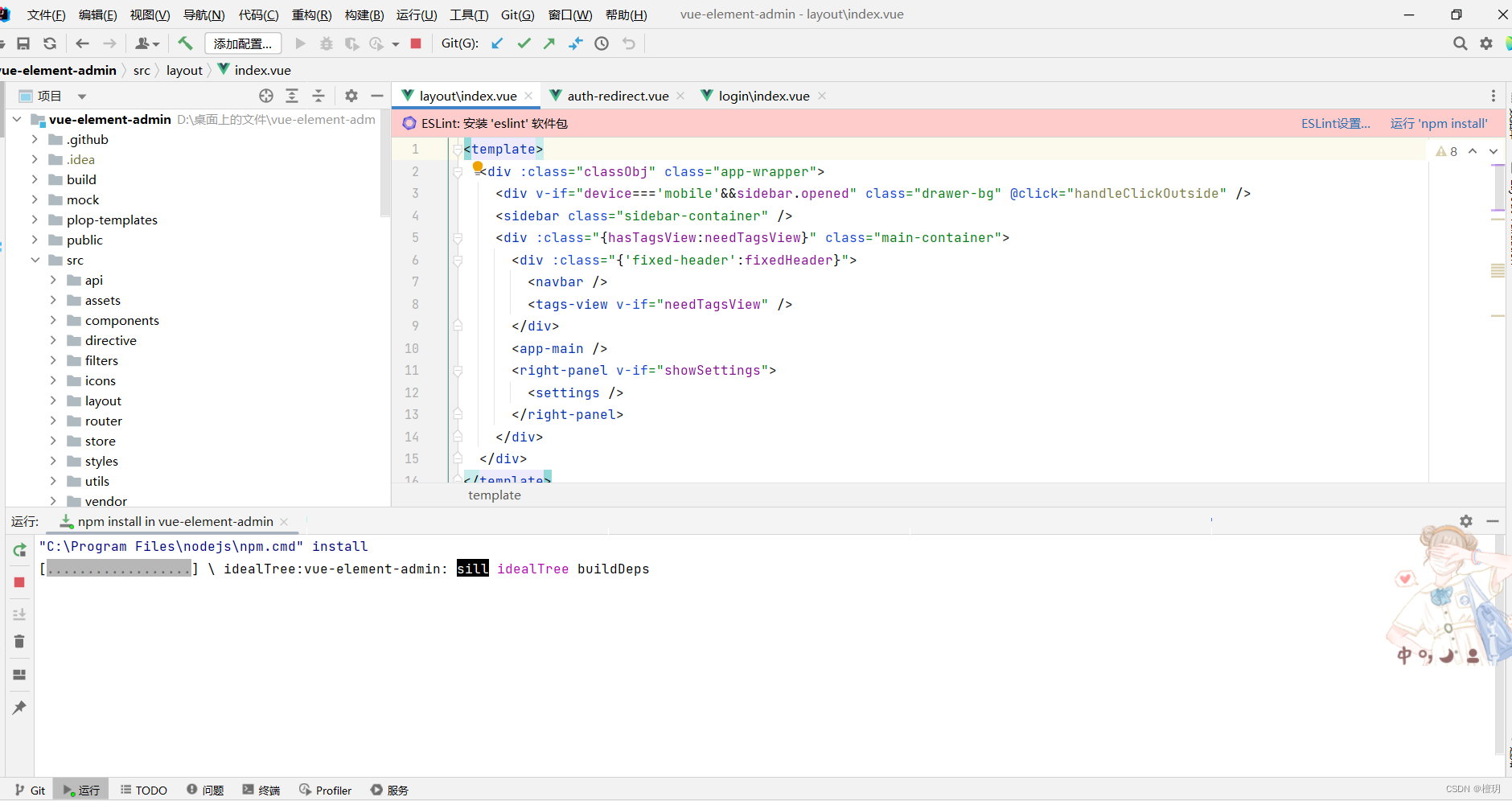
友好前端vue脚手架
企业级后台集成方案vue-element-admin-CSDN博客在哔站学习,老师说可以有直接的脚手架(vue-element-admin)立马去搜索,找到了这博主这篇文章 介绍 | vue-element-admin 官方默认英文版: git clone https:/…...
SQL Server特性
一、创建表 在sql server中使用create table来创建新表。 create table Customers( id int primary key identity(1,1), name varchar(5) ) 该表名为Customers其中包含了2个字段,分别为id(主键)以及name。 1、数据类型 整数类型ÿ…...

华为HCIP Datacom H12-821 卷25
1.单选题 Smurf攻击一般使用以下哪种协议 A、TCP B、BGP C、ICMP D、DHCP 正确答案: C 解析: Smurf攻击是一种病毒攻击,以最初发动这种攻击的程序“Smurf”来命名。这种攻击方法结合使用了IP欺骗和ICMP回复方法使大量网络传输充斥目…...

如何在 Selenium Python 中解决验证码 | 2024 完整指南
由于在进行网络自动化时遇到验证码是让许多人感到不知所措的问题。这些验证码专为区分人类用户和自动化脚本而设计,对于使用Selenium进行网络爬虫或自动化任务而言,无疑是一个巨大的挑战。2024年的完全指南将为您提供全面的解决方案,帮助您高…...

ASCII码对照表【2024年汇总】
🍺ASCII相关文章汇总如下🍺: 🎈ASCII码对照表(255个ascii字符汇总)🎈🎈ASCII码对照表(Unicode 字符集列表)🎈🎈ASCII码对照表&#x…...

刷题之买股票的最佳时机(leetcode)
买股票的最佳时机 动态规划入门题。 最简单的模拟式解法: class Solution { public:int maxProfit(vector<int>& prices) {//也可以换一种思路,因为只交易一次,那么找出股票最便宜的时候买入,最贵的时候卖出ÿ…...

Apache Seata透过源码解决SeataAT模式整合Mybatis-Plus失去MP特性的问题
本文来自 Apache Seata官方文档,欢迎访问官网,查看更多深度文章。 本文来自 Apache Seata官方文档,欢迎访问官网,查看更多深度文章。 Apache Seata透过源码解决SeataAT模式整合Mybatis-Plus失去MP特性的问题 透过源码解决SeataAT…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...

云原生时代的系统设计:架构转型的战略支点
📝个人主页🌹:一ge科研小菜鸡-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、云原生的崛起:技术趋势与现实需求的交汇 随着企业业务的互联网化、全球化、智能化持续加深,传统的 I…...

AT模式下的全局锁冲突如何解决?
一、全局锁冲突解决方案 1. 业务层重试机制(推荐方案) Service public class OrderService {GlobalTransactionalRetryable(maxAttempts 3, backoff Backoff(delay 100))public void createOrder(OrderDTO order) {// 库存扣减(自动加全…...
