《程序员面试金典(第6版)》面试题 04.05. 合法二叉搜索树
题目描述
实现一个函数,检查一棵二叉树是否为二叉搜索树。
示例 1:
输入:
2/ \1 3
输出: true
示例 2:
输入:
5/ \1 4/ \3 6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
根节点的值为 5 ,但是其右子节点值为 4 。
解题思路与代码
使用额外数据结构 + 中序遍历
这应该是最简单,并且最容易理解的一种做法了。
由二叉搜索树的性质可知,二叉搜索树的左边节点小于中间节点,中间节点小于右边节点。由这一特性我们可以得知,二叉搜索树的中序遍历是一个有序的数组。
我们只需要检查这个数组是否有序,就能判断出这个二叉树是否是二叉搜索树。
具体实现请看代码:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:bool isValidBST(TreeNode* root) {vector<int> result;inorderTraversal(root,result);int size = result.size();for(int i = 1; i < size; ++i )if(result[i-1] >= result[i]) return false;return true;}void inorderTraversal(TreeNode* root,vector<int>& vec){if(root == nullptr) return ;inorderTraversal(root->left,vec);vec.push_back(root->val);inorderTraversal(root->right,vec);}
};

复杂度分析
时间复杂度:O(n),n是这个二叉树的节点数目。我们要遍历这个二叉树的每一个节点。
空间复杂度:O(n),n是这个二叉树的节点数目,我们要将n个元素压入vector中。此外,函数的递归调用会使用一定的系统栈空间,但是由于递归深度不会超过二叉树的高度,所以可以认为空间复杂度也是 O(n) 级别的。
中序遍历不使用额外数据结构
这种做法,就是稍稍的将我刚刚的那种做法升级了一下,我们使用一个前驱指针,去记录中序遍历的前一个节点。那么中序遍历是先遍历左子树然后遍历中间节点,再去遍历右子树的。所以我们只需要一直去判断,这个前驱指针的值是否一种小于中间节点的值就行了。
具体实现请看代码:
class Solution {
public:TreeNode* pre = nullptr;bool isValidBST(TreeNode* root) {if(root == nullptr) return true;if(!isValidBST(root->left)) return false;if(pre != nullptr && pre->val >= root->val) return false;pre = root;if(!isValidBST(root->right)) return false;return true;}
};
注意:这个代码中不太容易想出来的代码在于这一行:if(!isValidBST(root->left)) return false; 我们的递归逻辑是在这个if判断里面的。这个递归就会把我们一直带到左叶子节点。然后再逐层的返回判断。

复杂度分析:
时间复杂度:O(n),n为节点的个数。不管怎样我们都要遍历这个树中的所有节点。
空间复杂度:O(h),其中 h 是二叉树的高度。最坏情况下(即二叉树退化为链表时),递归调用深度达到 n,此时栈的空间复杂度为 O(n);平均情况下树的高度是 log n,空间复杂度是 O(log n)。
这个代码优化了空间复杂度,因为没有用到额外的数据结构。但是执行代码所需要的时间缺增加了。这是因为我们每次递归都要做许多的判断。而上一次的代码只需要在for循环里做少量判断就行了。
总结
这道题不算太难。只要能及时的想起二叉搜索树的性质,就能轻松解题。
相关文章:

《程序员面试金典(第6版)》面试题 04.05. 合法二叉搜索树
题目描述 实现一个函数,检查一棵二叉树是否为二叉搜索树。 示例 1: 输入: 2/ \1 3输出: true 示例 2: 输入: 5/ \1 4/ \3 6输出: false 解释: 输入为: [5,1,4,null,null,3,6]。 根节点的值为 5 ,但是其右子节点值为 4 。 解题思路与代码 使用…...

Nginx 反向代理技术梳理
Nginx 反向代理技术梳理 使用反向代理脑图 域名 A 可以解析找到 CDN 缓存 用户点击 APP 即通过 URL 发送 HTTPS 请求域名会进入阿里云的 DNS 服务器,解析域名会做第一级负载均衡通过 CDN 解析出域名,通过阿里云配置转发到 CDN 缓存服务器 CDN 有数据则直…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 整数编码(Java) | 机试题+算法思路+考点+代码解析 【2023】
整数编码 题目 实现一种整数编码方法,使得待编码的数字越小,编码后所占用的字节数越小。 编码规则如下: 1、编码时7位一组,每个字节的低7位用于存储待编码数字的补码。 2、字节的最高位表示后续是否还有字节,置1表示后面还有更多的字节,置0表示当前字节为最后一个字…...

蓝桥杯冲击01 - 质数篇
目录 前言 一、质数是什么 二、易错点 三、试除法判断是否为质数 四、质数常考三大模型 五、真题练手 前言 距离蓝桥杯还有一个月,高效复习蓝桥杯知识, 质数相关的题目在蓝桥杯中经常出现。例如,2016年蓝桥杯省赛初赛第四题就是要求判…...

【WEB前端进阶之路】 HTML 全路线学习知识点梳理(下)
前言 本文是HTML零基础小白学习系列的第三篇文章,点此阅读 上一篇文章 文章目录前言十五.HTML布局1.使用div元素添加网页布局2.使用table元素添加网页布局十六.HTML表单和输入1.文本域2.密码字段3.单选按钮4.复选框5.提交按钮十七.HTML框架1.iframe语法2.iframe设置…...
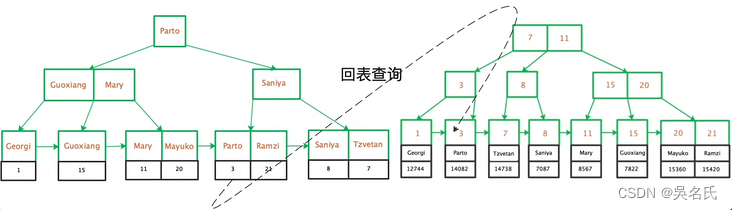
MySQL索引分类
1 MySQL索引都有哪些分类按数据结构分类可分为:Btree索引、Hash索引、Full-text索引;按物理存储分类可分为:聚簇索引、二级索引(辅助索引);按字段特性分类可分为:主键索引、普通索引、前缀索引;按字段个数分类可分为&a…...

会声会影2023最新版图文安装详细教程
会声会影2023操作简单,使用便捷,创意十足,新增的分屏功能,轨道透明度,镜头平移等功能,让用户的剪辑过程更加流畅,轻松就能制作出令人惊艳的视频作品。它不仅符合家庭或个人所需的影片剪辑功能&a…...
Java中的反射
类加载器(1)类的加载当我们的程序在运行后,第一次使用某个类的时候,会将此类的class文件读取到内存,并将此类的所有信息存储到一个Class对象中。说明:a.图中的Class对象是指:java.lang.Class类的…...

STM32入门笔记(03):STM32F103C8T6定时器的输入捕获模式和编码器模式(SPL库函数版)
目录1.定时器的输入捕获模式定时器输入捕获实验代码实现程序说明实现思路实现效果知识要点2.定时器的编码器模式定时器编码器实验代码实现实验思路知识要点参考资料先导知识 [1] STM32入门笔记(02):定时器之定时器中断、输入捕获和PWM输出(SPL库函数版)…...
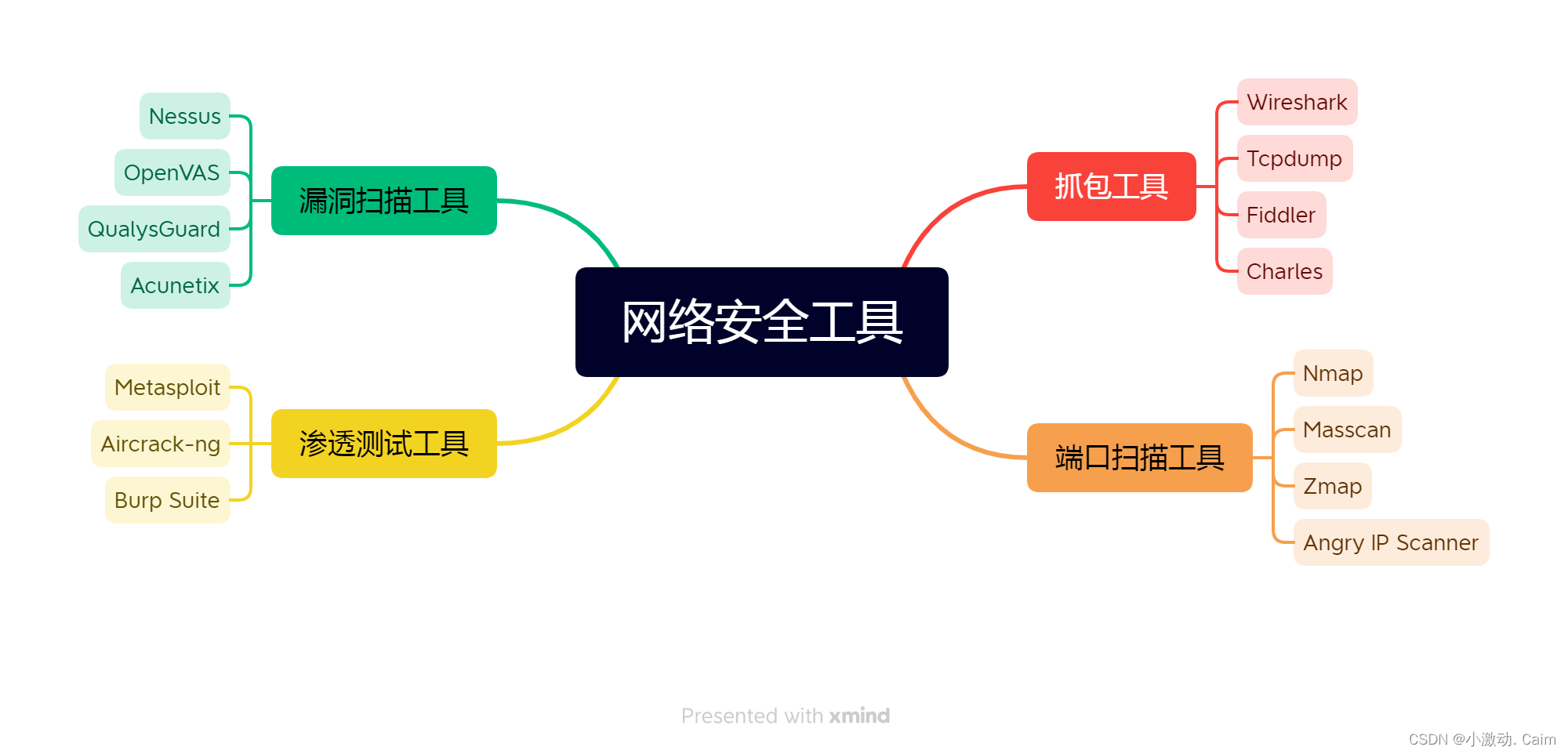
《网络安全》零基础教程-适合小白科普
《网络安全》零基础教程 目录 目录 《网络安全》零基础教程 第1章 网络安全基础 什么是网络安全 常见的网络安全威胁 网络安全的三个基本要素 网络安全的保障措施 第2章 网络攻击类型 病毒、蠕虫、木马、后门 DoS、DDoS攻击 SQL注入、XSS攻击 …...

微信小程序语言与web开发语言的区别
WXML与HTML的区别def:WXML是小程序框架设计的一套标签语言,用来构建小程序页面的结构,作用类似于web开发中的HTML区别:标签名称的不同如HTML中的div,span,img,a分别对应wxml中的view,…...
【2022-09-14】米哈游秋招笔试三道编程题
第一题:最短子串 题目描述 米小游拿到了一个字符串,她想截取一个连续子串,使得该子串中包含至少k个连续的“mihoyo”。 你可以帮米小游求出最短的子串长度,以及对应的子串位置吗? 输入描述 第一行输入两个正整数n…...

云监控能力介绍
传统监控介绍 监控系统必要性 监控系统的能力清单 市面上常见商业及开源监控工具集 传统监控体系的不足 云监控介绍 云监控(CloudMonitor)是一项针对云资源和互联网应用进行监控的服务。 云监控为云上用户提供开箱即用的企业级开放型一站式监控解决方…...

HTML 文档类型
<!DOCTYPE> 声明帮助浏览器正确地显示网页。 <!DOCTYPE> 声明 Web 世界中存在许多不同的文档。只有了解文档的类型,浏览器才能正确地显示文档。 HTML 也有多个不同的版本,只有完全明白页面中使用的确切 HTML 版本,浏览器才能完…...
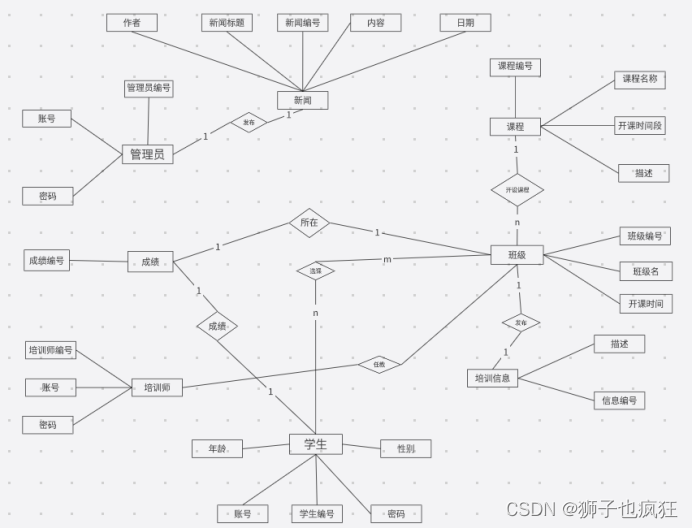
【UML】软件设计说明书 (完结)
目录一. 🦁 前言1.1 编写目的1.2 背景1.3 定义1.4 参考资料二. 🦁 总体设计2.1需求规定2.1.1 系统描述2.1.2 系统用例图2.2 运行环境2.2.1 设备2.2.2 支持软件2.2.3 接口2.2.4 控制2.3 基本设计概念2.4 系统结构三. 🦁 用例分析与设计3.1 用户…...
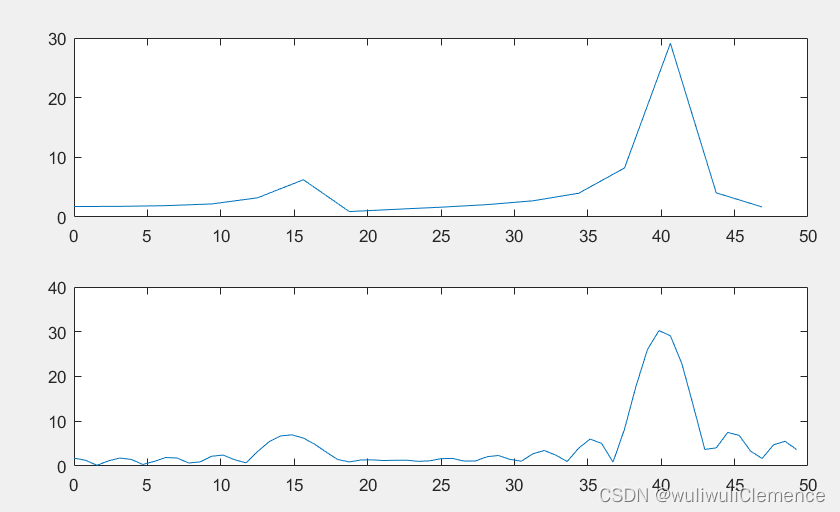
MATLAB——FFT(快速傅里叶变换)
基础知识 FFT即快速傅里叶变换,利用周期性和可约性,减少了DFT的运算量。常见的有按时间抽取的基2算法(DIT-FFT)按频率抽取的基2算法(DIF-FFT)。 1.利用自带函数fft进行快速傅里叶变换 若已知序列x[4,3,2,6…...

力扣-进店却未进行过交易的顾客
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:1581. 进店却未进行过交易的顾客二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行…...
一文解决vscode中借助CMake配置使用Opencv过程中的所有问题
vscode中借助CMake配置使用opencv过程中的问题 vscode编译工程的完整过程 编写好CMakeLists.txtvscode中 ctrlshiftp 选择cmake configurevscode中 ctrlshiftp 选择cmake build CMake问题 1. set OpenCV_FOUND to FALSE so package “OpenCV” is considered to be NOT FOU…...

Golang每日一练(leetDay0004)
10. 正则表达式匹配 Regular Expression Matching 给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 . 和 * 的正则表达式匹配。 . 匹配任意单个字符* 匹配零个或多个前面的那一个元素 所谓匹配,是要涵盖 整个 字符串 s的,而不是部分…...

手机忘记密码解锁的 6 大软件方法
您可能想要解锁手机的原因有很多。也许您正在海外旅行并想使用当地的 SIM 卡,或者您可能刚买了一部二手手机并且需要删除之前所有者的个人数据。您可能想知道如何获得可以免费解锁任何手机的软件。Android 用户可以使用他们的指纹、面部识别或 PIN。您也可以通过快速…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...
