Python28-7.5 降维算法之t-分布邻域嵌入t-SNE
t-分布邻域嵌入(t-distributed Stochastic Neighbor Embedding,t-SNE)是一种用于数据降维和可视化的机器学习算法,尤其适用于高维数据的降维。t-SNE通过将高维数据嵌入到低维空间(通常是二维或三维)中,使得在高维空间中相似的点在低维空间中仍然保持相似,而不相似的点被分离开来。
t-SNE的基本原理
t-SNE通过两步将高维数据降维:
-
计算高维空间中的相似性:在高维空间中,t-SNE使用高斯分布来计算数据点之间的相似性。给定数据点x_i和 x_j,其相似性 p_ij定义为:
这里,sigma_i 是根据Perplexity参数自动确定的。
-
计算低维空间中的相似性:在低维空间中,t-SNE使用t分布来计算数据点之间的相似性。给定低维数据点 y_i和 y_j,其相似性 q_ij定义为:
-
最小化KL散度:t-SNE通过最小化高维相似性分布 (P) 和低维相似性分布 (Q) 之间的Kullback-Leibler (KL) 散度来优化低维嵌入:
t-SNE的特点
-
保持局部结构:t-SNE在保持数据局部结构(局部相似性)方面表现非常好,能够揭示数据中的细节模式。
-
非线性降维:t-SNE是非线性降维方法,适合处理具有复杂非线性结构的数据。
-
高计算量:t-SNE计算量较大,尤其是在处理大规模数据集时。
t-SNE的应用
t-SNE广泛应用于数据可视化,特别是以下领域:
-
图像处理:用于高维图像特征的可视化。
-
自然语言处理:用于文本和词嵌入的可视化。
-
生物信息学:用于基因表达数据的可视化。
-
聚类分析:用于聚类结果的可视化。
示例代码
以下是使用Python库scikit-learn实现t-SNE的示例代码:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE
from sklearn.datasets import load_digits# 加载数据
digits = load_digits()
X = digits.data
y = digits.target# 使用t-SNE降维
tsne = TSNE(n_components=2, perplexity=30, n_iter=300)
X_embedded = tsne.fit_transform(X)# 可视化结果
plt.figure(figsize=(10, 8))
scatter = plt.scatter(X_embedded[:, 0], X_embedded[:, 1], c=y, cmap='viridis')
plt.colorbar(scatter)
plt.title("t-SNE visualization of the digits dataset")
plt.xlabel("t-SNE component 1")
plt.ylabel("t-SNE component 2")
plt.show()
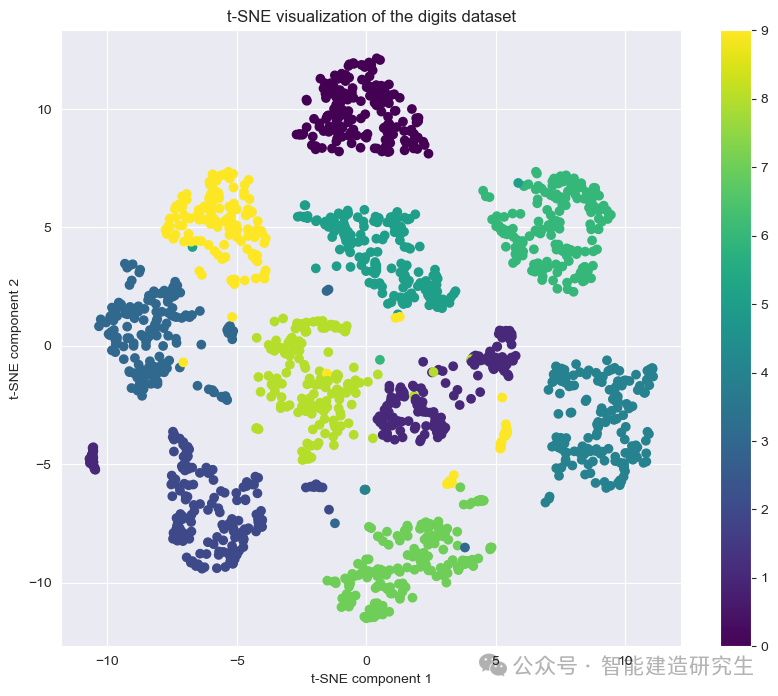
t-SNE的参数调整
-
Perplexity:影响高斯分布的方差,通常介于5到50之间,反映了考虑邻居数量的平衡。
-
学习率(learning_rate):影响梯度下降的步长,通常设置在10到1000之间。
-
迭代次数(n_iter):t-SNE优化过程的迭代次数,通常需要至少250次迭代,建议300次以上。
t-SNE是一种强大的非线性降维方法,特别适用于高维数据的可视化。通过保持高维数据的局部结构,它能够揭示数据中的复杂模式。然而,t-SNE的计算复杂度较高,需要合理选择参数来平衡性能和效果。
以上内容总结自网络,如有帮助欢迎转发,我们下次再见!
相关文章:

Python28-7.5 降维算法之t-分布邻域嵌入t-SNE
t-分布邻域嵌入(t-distributed Stochastic Neighbor Embedding,t-SNE)是一种用于数据降维和可视化的机器学习算法,尤其适用于高维数据的降维。t-SNE通过将高维数据嵌入到低维空间(通常是二维或三维)中&…...

一个最简单的comsol斜坡稳定性分析例子——详细步骤
一个最简单的comsol斜坡稳定性分析例子——详细步骤 标准模型例子—详细步骤 线弹性模型下的地应力平衡预应力与预应变、土壤塑性和安全系数求解的辅助扫描...

Java 变量类型
在Java中,变量类型包括基本数据类型和引用数据类型,每种类型有其特定的用途和存储方式。 ### 1. 基本数据类型 Java的基本数据类型包括整数类型、浮点类型、字符类型和布尔类型,它们分别是: - **整数类型**:用于存储…...
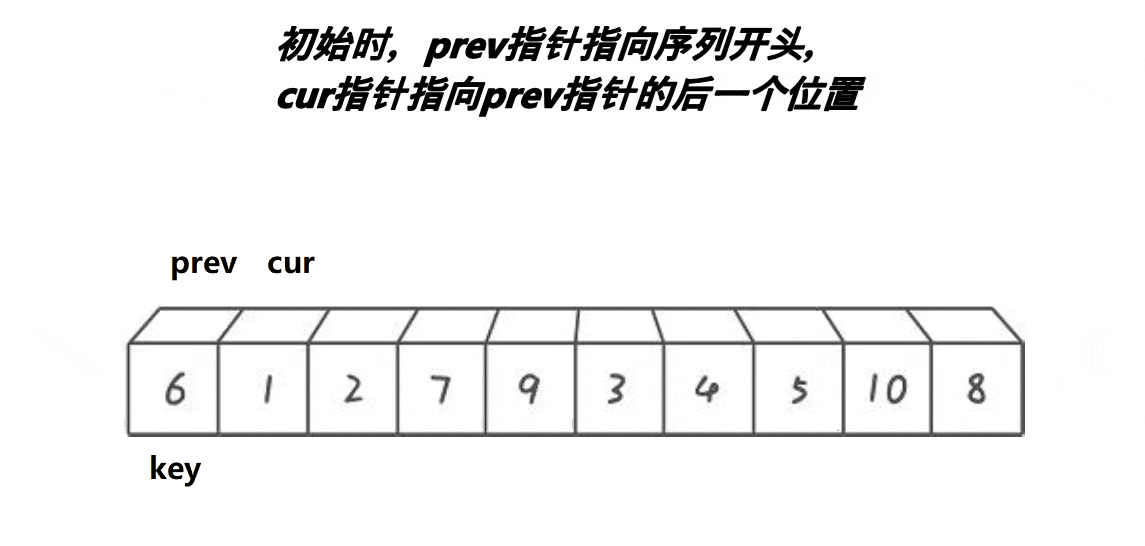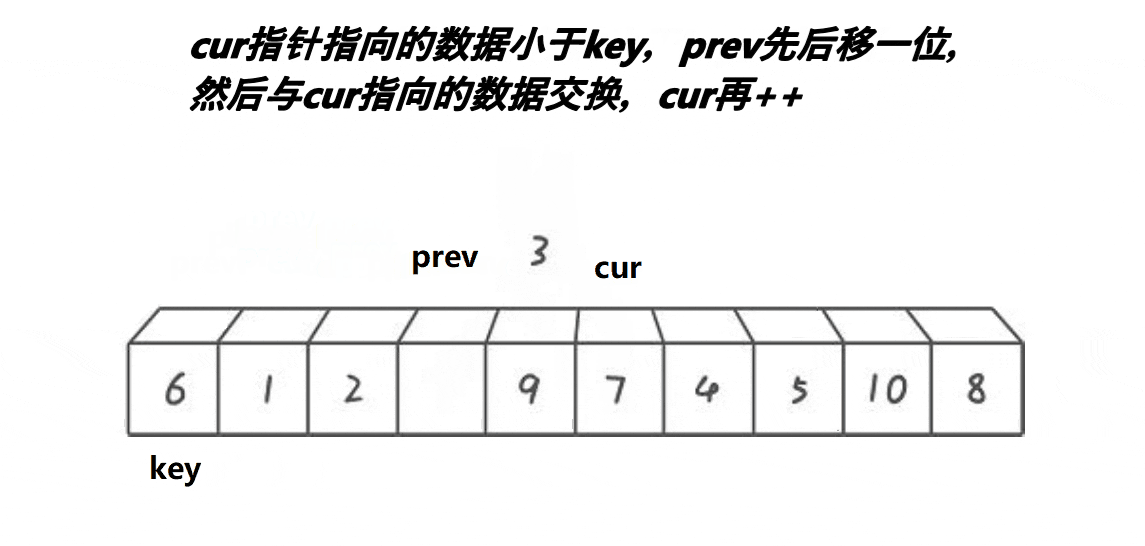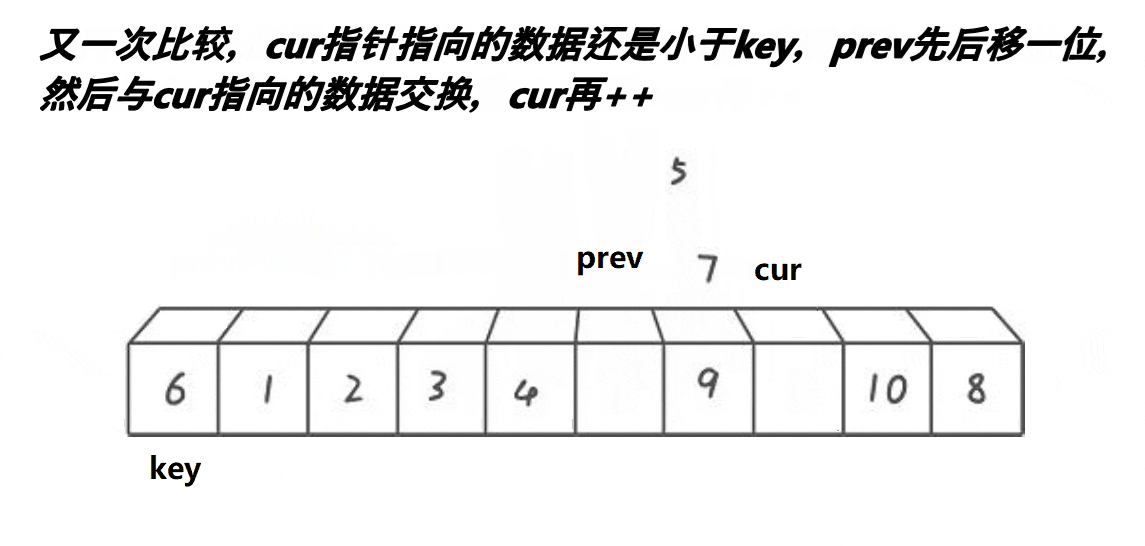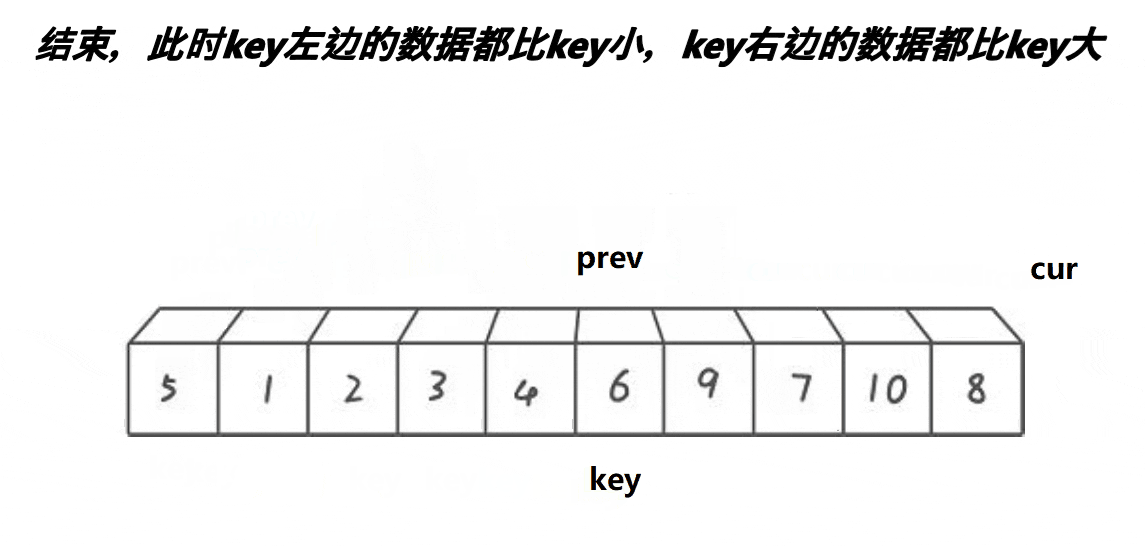
【排序算法】—— 快速排序
快速排序的原理是交换排序,其中qsort函数用的排序原理就是快速排序,它是一种效率较高的不稳定函数,时间复杂度为O(N*longN),接下来就来学习一下快速排序。 一、快速排序思路 1.整体思路 以升序排序为例: (1)、首先随…...
前端JS特效第22波:jQuery滑动手风琴内容切换特效
jQuery滑动手风琴内容切换特效,先来看看效果: 部分核心的代码如下: <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xm…...

redis的数据类型对应的使用场景
Redis提供了多种数据类型,每种数据类型都有其特定的适用场景。以下是Redis主要数据类型及其典型应用场景:1. 字符串(String) 应用场景:适用于存储简单的键值对数据,如用户基本信息、计数器(如网页访问次数&…...

ctfshow-web入门-命令执行(web118详解)Linux 内置变量与Bash切片
输入数字和小写字母,回显 evil input 查看源码,发现这里会将提交的参数 code 传给 system 函数 使用 burpsuite 抓包进行单个字符的模糊测试 fuzz: 发现过滤掉了数字和小写字母以及一些符号,下面框起来的部分是可用的 结合题目提…...

C语言 指针和数组——指针和二维数组之间的关系
目录 换个角度看二维数组 指向二维数组的行指针 按行指针访问二维数组元素 再换一个角度看二维数组 按列指针访问二维数组元素 二维数组作函数参数 指向二维数组的行指针作函数参数 指向二维数组的列指针作函数参数编辑 用const保护你传给函数的数据 小结 换个角度看…...
问题集锦1
01.inner中使用JwtTokenUtil.getUserCode() 前端调用上传(java),上传使用加购 Overridepublic Boolean insertShoppingCart(InsertShoppingCartParamsDto dto) {// 通过userCode,itemCode和supplierCode来判断当前加购人添加到购物车的商品是…...

浅析MySQL-索引篇01
什么是索引? 索引是帮助存储引擎快速获取数据的一种数据结构,类似于数据的目录。 索引的分类 按数据结构分类: MySQL 常见索引有 BTree 索引、HASH 索引、Full-Text 索引。 Innodb是MySQL5.5之后的默认存储引擎,BTree索引类型也…...

2028年企业云存储支出翻倍,达到1280亿美元
根据Omdia的研究,到2028年,企业云存储支出将从去年的570亿美元翻一番以上,达到1280亿美元。该研究分析了基础设施即服务(IaaS)和平台即服务(PaaS)数据中心的收入,作为年度存储数据服…...

ActiViz中的颜色映射表vtkLookupTable
文章目录 一、简介二、VtkLookupTable的创建与初始化三、设置数据范围四、颜色映射设置五、不透明度设置六、自定义颜色映射七、 不连续性颜色映射八、 预设颜色映射方案九、可视化效果优化十、与其他VTK组件的整合十一、 动态调整映射表十二、保存和加载颜色映射表一、简介 V…...

【Spring AOP 源码解析前篇】什么是 AOP | 通知类型 | 切点表达式| AOP 如何使用
前言(关于源码航行) 在准备面试和学习的过程中,我阅读了还算多的源码,比如 JUC、Spring、MyBatis,收获了很多代码的设计思想,也对平时调用的 API 有了更深入的理解;但过多散乱的笔记给我的整理…...

Laravel HTTP客户端:网络请求的瑞士军刀
标题:Laravel HTTP客户端:网络请求的瑞士军刀 Laravel的HTTP客户端是一个功能强大的工具,它提供了一种简洁、直观的方式来发送HTTP请求。无论是与外部API集成,还是进行网络数据抓取,Laravel的HTTP客户端都能满足你的需…...

7月07日,每日信息差
第一、6 月份,北京、上海、广州和深圳的新建商品住宅成交量分别环比增加 21%、66%、48% 和 38%,均创年内新高 第二、2024 年世界人工智能大会上,上海向四家企业发放了首批无驾驶人智能网联汽车示范应用许可,这些企业可以在浦东部…...

ubuntu 网络常用命令
在Ubuntu中,有许多网络相关的常用命令。以下是一些主要命令及其用途: ifconfig:此命令用于显示和配置网络接口信息。你可以使用它来查看IP地址、子网掩码、广播地址等。 例如:ifconfig 注意:在新版本的Linux发行版中…...
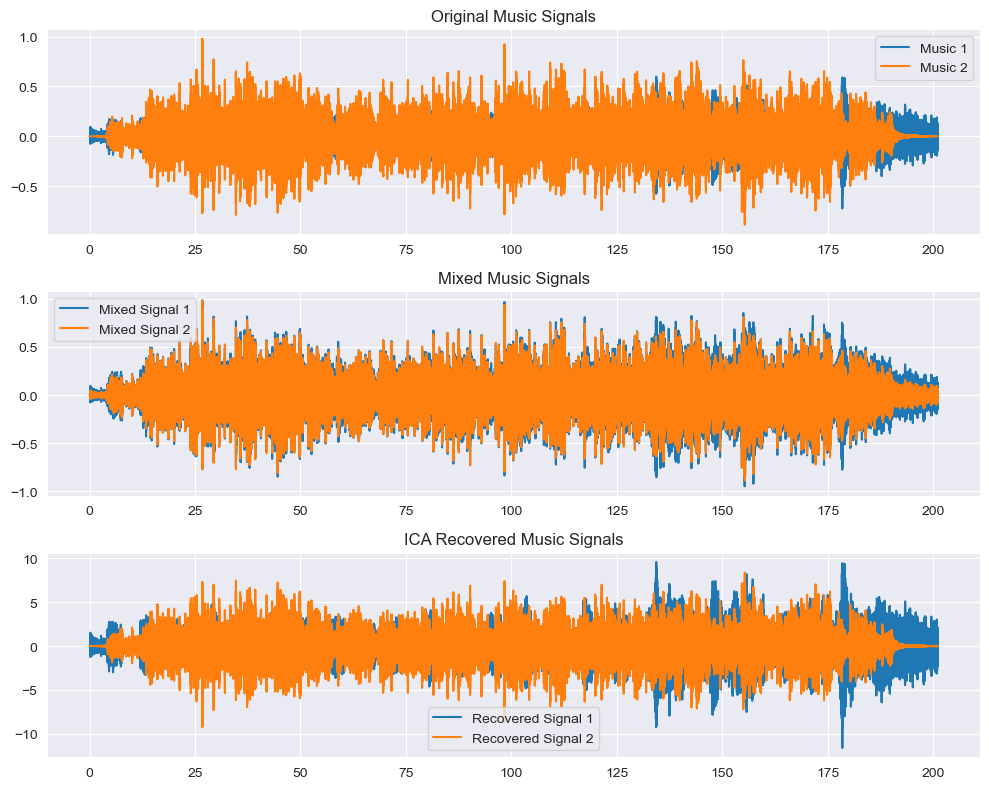
Python28-7.4 独立成分分析ICA分离混合音频
独立成分分析(Independent Component Analysis,ICA)是一种统计与计算技术,主要用于信号分离,即从多种混合信号中提取出独立的信号源。ICA在处理盲源分离(Blind Source Separation,BSS࿰…...

Spring Boot与Okta的集成
Spring Boot与Okta的集成 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将探讨如何在Spring Boot应用中集成Okta,实现身份认证和授权的功能…...
模式)
MVC(Model-View-Controller)模式
MVC(Model-View-Controller)模式三个主要组件:模型(Model),视图(View),和控制器(Controller): 模型(Model)&a…...

MuLan:模仿人类画家的多对象图像生成
在图像生成领域,处理包含多个对象及其空间关系、相对大小、重叠和属性绑定的复杂提示时,现有的文本到图像模型仍面临挑战:当文本提示中包含多个对象,并且这些对象之间存在特定的空间关系时,现有模型往往难以准确地捕捉…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现指南针功能
指南针功能是许多位置服务应用的基础功能之一。下面我将详细介绍如何在HarmonyOS 5中使用DevEco Studio实现指南针功能。 1. 开发环境准备 确保已安装DevEco Studio 3.1或更高版本确保项目使用的是HarmonyOS 5.0 SDK在项目的module.json5中配置必要的权限 2. 权限配置 在mo…...
