基于现有Docker镜像构建新的Docker镜像
1.拉取ubuntu 22.04的系统镜像
docker pull ubuntu:22.04 
拉取成功后在DockerDesktop中可发现该镜像

2.启动刚才接取的ubuntu镜像
docker run --name Ubuntu22.04 -it -d -p 22:22 -p 80:80 -p 443:443 340d9b015b194dc6e2a13938944e0d016e57b9679963fdeb9ce021daac430221启动成功会返回容器ID

查看启动的镜像:
docker ps
启动成功后,dockerdesktop中也可看到容器信息:

3.在dockerdesktop中的容器标签找到启动的窗口进行Exec中执行下面命令,安装 go环境
apt update && apt upgrade && apt install golang  4.重新封装镜像:
4.重新封装镜像:
下面为当前容器ID
ad73872b4f175b0de1c9c9fbe077b1a53590ce2ebf81ea26f4a1d972381ff24c使用当前容器封装新镜像 ,ubuntu-go:22.04为镜像名,reverse为镜像作者
Ubuntu22.04 With GO ENV为镜像描述
docker commit -m "Ubuntu22.04 With GO ENV" -a "reverse" ad73872b4f175b0de1c9c9fbe077b1a53590ce2ebf81ea26f4a1d972381ff24c ubuntu-go:22.04封装成功会返回新镜像ID:

新镜像ID:
f849fa5d8b3688db2d93be8555f5c07af14660222888e1562edebfa66797d93ddockerdesktop中可看到封装成功的镜像

启动新封装的镜像ubuntu-go
docker run --name Ubuntu-Go-22.04 -p 22:22 -p 80:80 -p 443:443 -it -d ubuntu-go:22.04
查看已启动的新容器


相关文章:

基于现有Docker镜像构建新的Docker镜像
1.拉取ubuntu 22.04的系统镜像 docker pull ubuntu:22.04 拉取成功后在DockerDesktop中可发现该镜像 2.启动刚才接取的ubuntu镜像 docker run --name Ubuntu22.04 -it -d -p 22:22 -p 80:80 -p 443:443 340d9b015b194dc6e2a13938944e0d016e57b9679963fdeb9ce021daac430221 启…...

Java 静态变量、静态代码块、普通代码块、构造方法的执行顺序
今天碰到这个问题,看了课程以及资料,做出解答。这是我自己绘制的图,按从上到下,从左到右的顺序执行。如有问题请联系我修正。 要点: 1、执行顺序分为两步,类加载和初始化阶段。 2、因为静态变量和静态代码块…...

计算机网络性能指标概述:速率、带宽、时延等
在计算机网络中,性能指标是衡量网络效率和质量的重要参数。本文将综合三篇关于计算机网络性能指标的文章,详细介绍速率、带宽、吞吐量、时延、时延带宽积、往返时延(RTT) 和利用率的概念及其在网络中的应用。 1. 速率(…...

众所周知沃尔玛1P是怎么运营?
沃尔玛的1P模式,即第一方供应商模式,是其独特的采购策略。在这种模式下,供应商先将商品卖给沃尔玛,由沃尔玛负责库存管理和销售。沃尔玛通过强大的采购和物流能力控制库存,确保商品品质,为客户提供更加…...
【Linux】静态库的制作和使用详解
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...

2.贪心算法.基础
2.贪心算法.基础 基础知识题目1.分发饼干2.摆动序列2.1.思路二:动态规划法 3.最大子序和4.买股票的最佳时机24.1.思路二:动态规划法4.2.买股票的最佳时机 5.跳跃游戏5.1.跳跃游戏2 6.K次取反后最大化的数组和7.加油站8.分发糖果 总结 基础知识 什么是贪…...

用Python轻松转换PDF为CSV
数据的可访问性和可操作性是数据管理的核心要素。PDF格式因其跨平台兼容性和版面固定性,在文档分享和打印方面表现出色,尤其适用于报表、调查结果等数据的存储。然而,PDF的非结构化特性限制了其在数据分析领域的应用。相比之下,CS…...

关于微信支付-商户平台:查询订单提示“查询失败:操作失败,请稍候重试”的分析
目录 引子 分析 应对 小结 引子 在开发和实施微信 JSAPI 支付的应用后,我们遇到了一些问题,订单的状态更新不正常,当然我们首先需要从自身寻找原因和完善解决问题的办法和方案。在支付的过程中,客户会给我们一些反馈…...

掌握【Python异常处理】:打造健壮代码的现代编程指南
目录 编辑 1. 什么是异常? 知识点 示例 小李的理解 2. 常见的内置异常类型 知识点 示例 小李的理解 3. 异常机制的意义 知识点 示例 小李的理解 4. 如何处理异常 知识点 示例 小李的理解 5. 抛出异常 知识点 示例 小李的理解 6. Python内置…...

STM32点灯闪烁
stm32c8t6引脚图 开发板引脚图 GPIO端口的每个位可以由软件分别配置成 多种模式。 ─ 输入浮空 ─ 输入上拉 ─ 输入下拉 ─ 模拟输入 ─ 开漏输出 ─ 推挽式输出 ─ 推挽式复用功能 ─ 开漏复用功能 配置GPIO端口步骤:开启时钟->使用结构体设置输出模式…...

Java-01-源码篇-04集合-05-SortedMap NavigableMap TreeMap
目录 一,SortedMap 二,NavigableMap 三,TreeMap 3.1 TreeMap 继承结构 3.2 TreeMap 属性 3.3 TreeMap 构造器 3.4 TreeMap 内部类 3.4.1 Values 3.4.2 KeySet 3.4.3 EntrySet 3.4.5 相关集合迭代器 3.4.5.1 PrivateEntryIterato…...
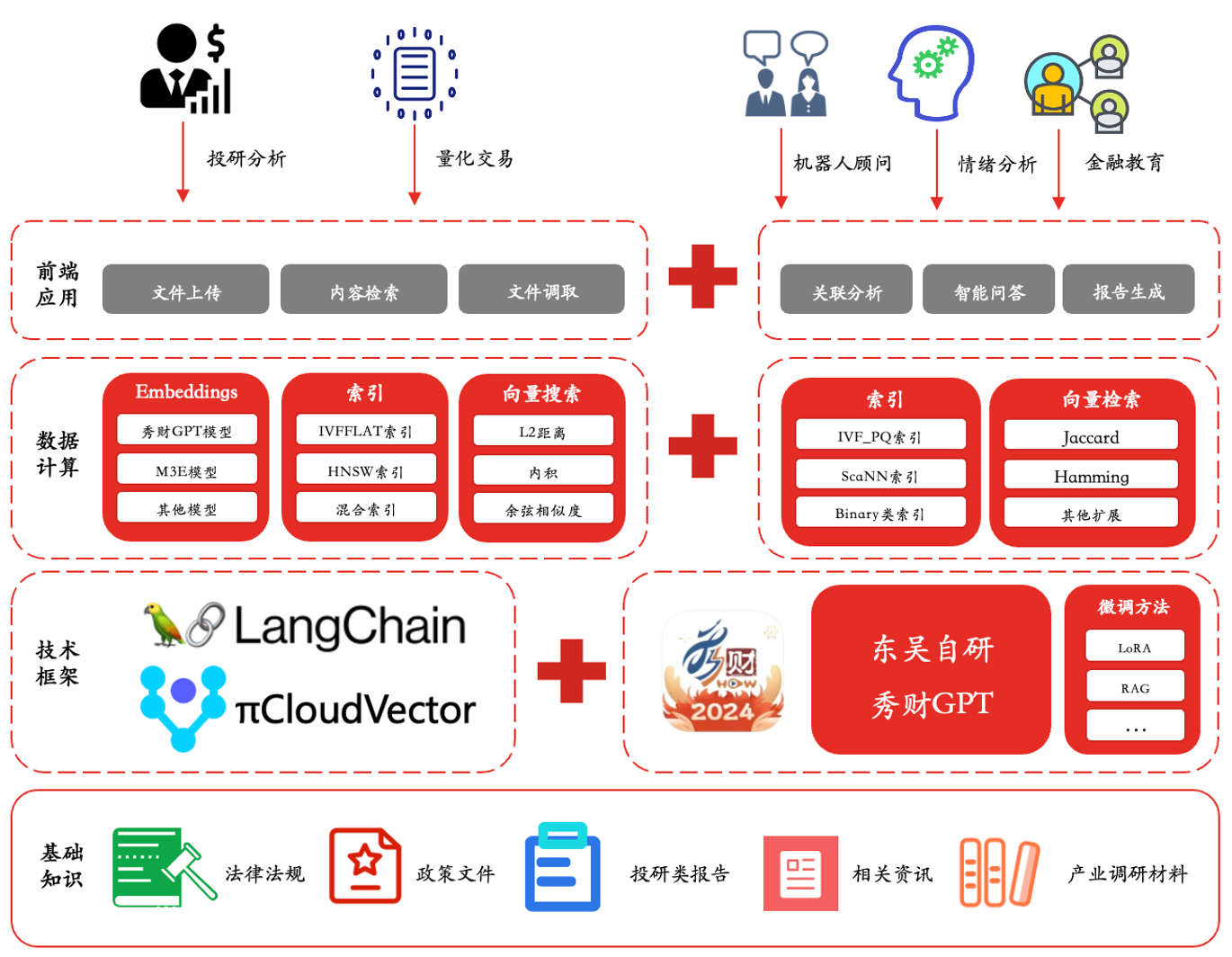
拥抱 AGI:PieDataCS 引领云原生数据计算系统新范式
自2023年后,人工智能技术进入了一个更为成熟和广泛应用的阶段,人工通用智能(AGI)这一概念也成为了科技界和产业界热议的焦点。本文将结合 AGI 时代背景,从架构设计到落地实践,详细介绍拓数派云原生数据计算…...

开放式耳机哪个品牌好?开放式耳机推荐
开放式耳机因其独特的设计,提供了更自然的听音体验和更好的环境声音感知,尤其适合长时间佩戴和户外运动使用,下面来推荐几款表现出色的开放式耳机: 悠律ringbuds pro凝声环(499元):凭借时尚潮流…...
kubernetes dashboard安装
1.查看符合自己版本的kubernetes Dashboard 比如我使用的是1.23.0版本 https://github.com/kubernetes/dashboard/releases?page5 对应版本 kubectl apply -f https://raw.githubusercontent.com/kubernetes/dashboard/v2.5.1/aio/deploy/recommended.yaml修改对应的yaml,…...

【MySQL】3.表的操作
表的操作 一.创建表二.查看表三.修改表四.删除表 一.创建表 create table [if not exists] tb_name( field1 datatype comment 说明, field2 datatype, field3 datatype) charsetutf8 collateutf8_gerenal_ci engineInnoDB//表的编码集,校验集如果不指定ÿ…...

十一、作业
1.从大到小输出 写代码将三个整数数按从大到小输出。 void Swap(int* px, int* py) {int tmp *px;*px *py;*py tmp;} int main() {int a 0;int b 0;int c 0;scanf("%d %d %d", &a, &b, &c);int n 0;if (a<b){Swap(&a, &b);}if (a &l…...

关于C#在WPF中如何使用“抽屉”控件
关于C#在WPF中如何使用“抽屉”控件 1.前提准备2.XAML代码3.对应的C#代码4.显示效果 1.前提准备 需要引用MaterialDesign控件库,关于如何引用,请参照文章——关于C#如何引用MaterialDesign控件库 2.XAML代码 <Window x:Class"MaterialDesign_…...

运维Tips | Ubuntu 24.04 安装配置 xrdp 远程桌面服务
[ 知识是人生的灯塔,只有不断学习,才能照亮前行的道路 ] Ubuntu 24.04 Desktop 安装配置 xrdp 远程桌面服务 描述:Xrdp是一个微软远程桌面协议(RDP)的开源实现,它允许我们通过图形界面控制远程系统。这里使…...

ExcelVBA运用Excel的【条件格式】(二)
ExcelVBA运用Excel的【条件格式】(二) 前面知识点回顾 1. 访问 FormatConditions 集合 Range.FormatConditions 2. 添加条件格式 FormatConditions.Add 方法 语法 表达式。添加 (类型、 运算符、 Expression1、 Expression2) 3. 修改或删除条件…...

肠道和大脑中犬尿氨酸代谢途径的紊乱
新出现的证据表明,肠道微生物群可能与宿主大脑相互作用,并在神经精神疾病的发病机制中发挥关键作用。然而,抑郁症中微生物-肠-脑轴相互作用的潜在机制仍不清楚。在这项研究中,建立了慢性约束应激 (CRS) 的小鼠模型,以研…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...
