Python蓝桥杯训练:基本数据结构 [二叉树] 中
Python蓝桥杯训练:基本数据结构 [二叉树] 中
文章目录
- Python蓝桥杯训练:基本数据结构 [二叉树] 中
- 一、[翻转二叉树](https://leetcode.cn/problems/invert-binary-tree/)
- 二、[对称二叉树](https://leetcode.cn/problems/symmetric-tree/)
- 三、[二叉树的最大深度](https://leetcode.cn/problems/maximum-depth-of-binary-tree/)
- 四、[二叉树的最小深度](https://leetcode.cn/problems/minimum-depth-of-binary-tree/)
- 五、[完全二叉树的节点个数](https://leetcode.cn/problems/count-complete-tree-nodes/)
- 六、[平衡二叉树](https://leetcode.cn/problems/balanced-binary-tree/)
一、翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:

输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:

输入:root = [2,1,3]
输出:[2,3,1]
示例 3:
输入:root = []
输出:[]
提示:
- 树中节点数目范围在
[0, 100]内 -100 <= Node.val <= 100
这道题目要求我们翻转一棵二叉树,可以使用递归的思路来解决问题。对于一个二叉树而言,可以将它的左右子树看作两个独立的小问题,因此可以先将左右子树分别翻转,然后再将整个树进行翻转。
具体实现时,可以编写一个递归函数,对于每一个节点而言,先分别翻转左右子树,然后将左右子树交换即可。如果节点为空,直接返回即可。
class Solution:def invertTree(self, root: TreeNode) -> TreeNode:if not root:return None# 递归翻转左右子树left = self.invertTree(root.left)right = self.invertTree(root.right)# 交换左右子树root.left = rightroot.right = leftreturn root
上面算法我们使用的遍历顺序是后序遍历,使用前序遍历也可以解决,该算法的时间复杂度为 O(n)O(n)O(n),其中 nnn 是二叉树的节点个数,因为每个节点都会被访问一次。空间复杂度为 O(n)O(n)O(n),因为递归函数会使用系统栈,最坏情况下系统栈的深度等于二叉树的高度,即为 O(n)O(n)O(n)。
二、对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:

输入:root = [1,2,2,3,4,4,3]
输出:true
示例 2:

输入:root = [1,2,2,null,3,null,3]
输出:false
提示:
- 树中节点数目在范围
[1, 1000]内 -100 <= Node.val <= 100
**进阶:**你可以运用递归和迭代两种方法解决这个问题吗?
首先,可以通过递归的方法来判断一棵二叉树是否是镜像对称的。对于一棵二叉树而言,如果它是镜像对称的,那么它的左右子树也是镜像对称的。因此,可以编写一个递归函数来判断左右子树是否镜像对称,然后判断根节点的左右子树是否镜像对称即可。
具体实现时,可以编写一个递归函数 isMirror,该函数接受两个参数 left 和 right,分别表示两棵子树。如果两棵子树均为空,返回 True;如果其中一棵子树为空,返回 False;如果两棵子树的根节点的值不相等,返回 False;否则,递归判断两棵子树的左右子树是否镜像对称。
class Solution(object):def isSymmetric(self, root):# 如果二叉树为空,则直接返回 Trueif not root:return True# 如果二叉树不为空,则递归判断其左右子树是否镜像对称return self.isMirror(root.left, root.right)def isMirror(self, left, right):# 如果两棵二叉树均为空,则返回 Trueif not left and not right:return True# 如果其中一棵二叉树为空,则返回 Falseif not left or not right:return False# 如果两棵二叉树的根节点的值不相等,则返回 Falseif left.val != right.val:return False# 递归判断两棵二叉树的左右子树是否镜像对称return self.isMirror(left.left, right.right) and self.isMirror(left.right, right.left)
三、二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3/ \9 20/ \15 7
返回它的最大深度 3 。
题目要求找出二叉树的最大深度,因此可以通过深度优先搜索的方式,而且推荐使用后序遍历来遍历二叉树,记录每个节点的深度,然后返回最大深度即可。
具体实现时,可以编写一个递归函数 maxDepth,该函数接受一个参数 node,表示当前节点。如果当前节点为空,则返回 0;否则,分别递归遍历当前节点的左右子树,返回左右子树深度的较大值加上 1,即为当前节点的深度。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution(object):def maxDepth(self, root):# 如果二叉树为空,则返回 0if not root:return 0# 分别递归遍历当前节点的左右子树left_depth = self.maxDepth(root.left)right_depth = self.maxDepth(root.right)# 返回左右子树深度的较大值加上 1,即为当前节点的深度return max(left_depth, right_depth) + 1
四、二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
**说明:**叶子节点是指没有子节点的节点。
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:2
示例 2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
提示:
- 树中节点数的范围在
[0, 105]内 -1000 <= Node.val <= 1000
题目要求找出二叉树的最小深度,因此我妈可以通过深度优先搜索的方式来遍历二叉树,记录每个节点的深度,然后返回最小深度即可。
具体实现时,可以编写一个递归函数 minDepth,该函数接受一个参数 node,表示当前节点。如果当前节点为空,则返回 0;否则,分别递归遍历当前节点的左右子树,如果当前节点有左右子树,则返回左右子树深度的较小值加上 1,否则返回左右子树深度的较大值加上 1,即为当前节点的深度。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution(object):def minDepth(self, root):# 如果二叉树为空,则返回 0if not root:return 0# 分别递归遍历当前节点的左右子树left_depth = self.minDepth(root.left)right_depth = self.minDepth(root.right)if not root.left or not root.right:# 如果当前节点只有一个子节点,则返回另一个子树的深度加上 1return left_depth + right_depth + 1else:# 如果当前节点有左右子树,则返回左右子树深度的较小值加上 1return min(left_depth, right_depth) + 1
这里需要注意的是,在计算当前节点只有一个子节点的情况时,我们需要将其另一个子树的深度加上 1,因为当前节点不是叶子节点,而是只有一个子节点的非叶子节点。
五、完全二叉树的节点个数
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2h 个节点。
示例 1:

输入:root = [1,2,3,4,5,6]
输出:6
示例 2:
输入:root = []
输出:0
示例 3:
输入:root = [1]
输出:1
提示:
- 树中节点的数目范围是
[0, 5 * 104] 0 <= Node.val <= 5 * 104- 题目数据保证输入的树是 完全二叉树
**进阶:**遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗?
在这里我们可以直接当作普通二叉树来处理,也就是之前练习的层序遍历,直接使用那个模板,记录遍历的节点数量就可以了。
在这里我们主要来着重利用完全二叉树的性质来解决问题,由于完全二叉树的特殊性质,我们可以先分别求出左子树和右子树的高度,然后根据它们的高度分情况讨论。
- 如果左右子树的高度相同,说明左子树是一棵满二叉树,右子树是一棵完全二叉树,那么左子树的节点个数可以直接计算,右子树的节点个数可以递归地求解。
- 如果左右子树的高度不同,说明右子树是一棵满二叉树,左子树是一棵完全二叉树,那么右子树的节点个数可以直接计算,左子树的节点个数可以递归地求解。
最终,根据上述讨论的结果,我们可以递归地求解出完全二叉树的节点个数。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution(object):def countNodes(self, root):if not root:return 0# 分别求出左子树和右子树的高度left_height = self.get_height(root.left)right_height = self.get_height(root.right)# 如果左右子树的高度相同,说明左子树是一棵满二叉树,右子树是一棵完全二叉树if left_height == right_height:# 左子树的节点个数可以直接计算return (1 << left_height) + self.countNodes(root.right)# 如果左右子树的高度不同,说明右子树是一棵满二叉树,左子树是一棵完全二叉树else:# 右子树的节点个数可以直接计算return (1 << right_height) + self.countNodes(root.left)def get_height(self, node):height = 0while node:height += 1node = node.leftreturn height
我们也可以换一个实现思路,首先判断二叉树是否为空,若为空则节点个数为0,直接返回;否则,记录左子树和右子树的根节点,同时记录左子树和右子树的深度,初始值都为0。
接着,通过循环,不断地遍历左子树和右子树,直到无法遍历,统计出左子树和右子树的深度。
如果左子树的深度等于右子树的深度,说明左子树是满二叉树,右子树是完全二叉树,此时可以利用满二叉树的节点数公式计算出总节点数,即 2leftDepth+1−12^{leftDepth+1}-12leftDepth+1−1,其中 leftDepthleftDepthleftDepth 表示左子树的深度。
如果左子树的深度不等于右子树的深度,说明左子树是完全二叉树,右子树是满二叉树,此时可以递归计算左子树和右子树的节点个数,并将它们加起来再加上根节点,即可得到总节点数。
最终返回计算出的节点数即可。
class Solution:def countNodes(self, root) -> int:if not root:return 0left = root.leftright = root.rightleftDepth = 0 #这里初始为0是有目的的,为了下面求指数方便rightDepth = 0while left: #求左子树深度left = left.leftleftDepth += 1while right: #求右子树深度right = right.rightrightDepth += 1if leftDepth == rightDepth:return (2 << leftDepth) - 1 #注意(2<<1) 相当于2^2,所以leftDepth初始为0return self.countNodes(root.left) + self.countNodes(root.right) + 1
六、平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:true
示例 2:

输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
示例 3:
输入:root = []
输出:true
提示:
- 树中的节点数在范围
[0, 5000]内 -104 <= Node.val <= 104
首先我们需要思考的是对于一棵二叉树,如果它是一棵空树,则它是平衡二叉树,因为它没有任何节点,高度为0。
接着,我们可以通过递归的方式判断以每个节点为根的子树是否是平衡二叉树。
对于每个节点,我们需要计算它的左子树和右子树的高度,并判断它们的高度差是否大于1,如果大于1,则说明该节点的子树不是平衡二叉树;否则,递归判断它的左子树和右子树是否是平衡二叉树,如果左子树和右子树都是平衡二叉树,则该节点的子树也是平衡二叉树。
最终,如果整个二叉树是平衡二叉树,则返回True,否则返回False。
class Solution:def isBalanced(self, root) -> bool:# 调用方法 getHeight 来获取二叉树的高度if self.getHeight(root) != -1:return Trueelse:return Falsedef getHeight(self, root):# 如果当前节点是空节点,则返回0if not root:return 0# 分别计算当前节点的左右子树的高度# 如果左右子树的高度差大于1,则说明该节点不是平衡二叉树,返回-1# 否则,返回该节点的高度if (leftHeight := self.getHeight(root.left)) == -1:return -1if (rightHeight := self.getHeight(root.right)) == -1:return -1if abs(leftHeight - rightHeight) > 1:return -1else:return 1 + max(leftHeight, rightHeight)
相关文章:

Python蓝桥杯训练:基本数据结构 [二叉树] 中
Python蓝桥杯训练:基本数据结构 [二叉树] 中 文章目录Python蓝桥杯训练:基本数据结构 [二叉树] 中一、[翻转二叉树](https://leetcode.cn/problems/invert-binary-tree/)二、[对称二叉树](https://leetcode.cn/problems/symmetric-tree/)三、[二叉树的最…...
 – UDS 协议)
读取 DTC 信息服务 (0x19) – UDS 协议
总目录链接>> AutoSAR入门和实战系列总目录 0x19读取 DTC 信息服务概述 读取 DTC 信息服务在 UDS 协议中用于从车辆或特定 ECU 或节点读取 DTC。UDS 协议的主要任务之一是故障诊断。每当车辆发生任何故障时,与该故障相对应的诊断故障代码(DTC&a…...

Hive 分区表新增字段 cascade
背景 在以前上线的分区表中新加一个字段,并且要求添加到指定的位置列。 模拟测试 加 cascade 操作 创建测试表 create table if not exists sqltest.table_add_column_test(org_col1 string comment 原始数据1,org_col2 string comment 原始数据2 ) comment 增…...

【Java版oj】day08两种排序方法、最小公倍数
目录 一、两种排序方法 (1)原题再现 (2)问题分析 (3)完整代码 二、最小公倍数 (1)原题再现 (2)问题分析 (3)完整代码 一、两种…...

FinOps,从概念到落地 | UGeek大咖说第一期直播回顾(上)
2023年2月28日,由优维科技联合FinOps产业推进方阵举办了第1期「UGeek大咖说-极致用云共济FinOps」线上直播活动,来自中国信通院及美图公司技术专家共同带来了一场精彩的技术视听盛宴。 直 播 背 景 目前,许多以“上云”为数字化转型路径的企…...

k8s java程序实现kubernetes Controller Operator 使用CRD 学习总结
k8s java程序实现kubernetes Controller & Operator 使用CRD 学习总结 大纲 原理Controller 与 Operator自定义资源定义 CRD ( CustomResourceDefinition)kubernetes-client使用java fabric8io/kubernetes-client操作k8s 原生资源使用java abric8io/kubernetes-clientt操…...
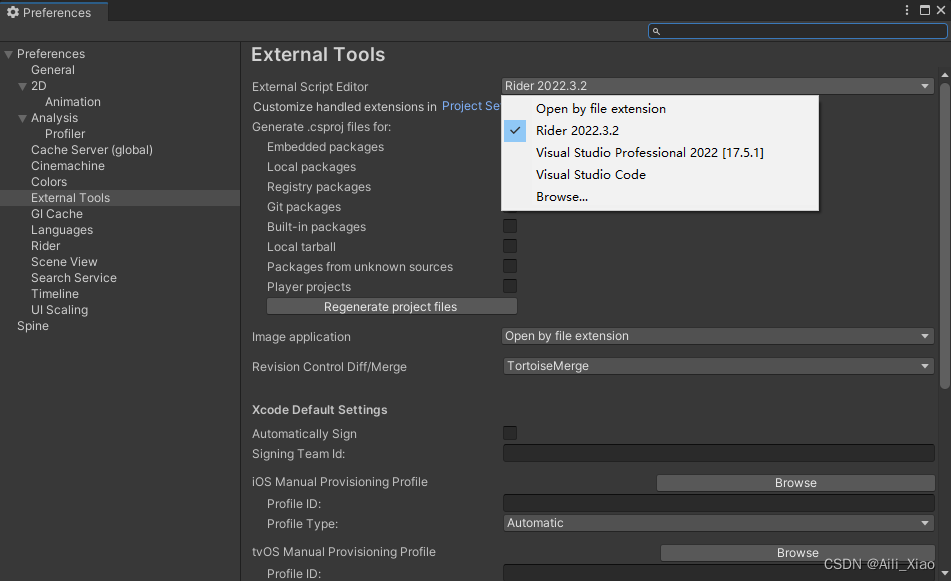
Unity笔记:修改代码执行的默认打开方式
使用 External Tools 偏好设置可设置用于编写脚本、处理图像和进行源代码控制的外部应用程序。 External Script Editor:选择 Unity 应使用哪个应用程序来打开脚本文件。Unity 会自动将正确的参数传递给内置支持的脚本编辑器。Unity 内置支持 Visual Studio Commun…...

Linux IPC:匿名管道 与 命名管道
目录一、管道的理解二、匿名管道三、命名管道四、管道的通信流程五、管道的特性进程间通信方式有多种,本文介绍的是管道,管道分为匿名管道和命名管道。 一、管道的理解 生活中的管道用来传输资源,例如水、石油之类的资源。而进程间通信的管道…...

阿里研发工程师JAVA暑期实习一面
文章目录先说一下我自己的情况面试过程总结先说一下我自己的情况 我就读于湖南大学,软件工程专业,现在大三下 很巧的是,我在大二的时候就在相同的时间面过相同的部门和相同的岗位,所以我没有做笔试就直接让我去面试了。我当时还纳…...
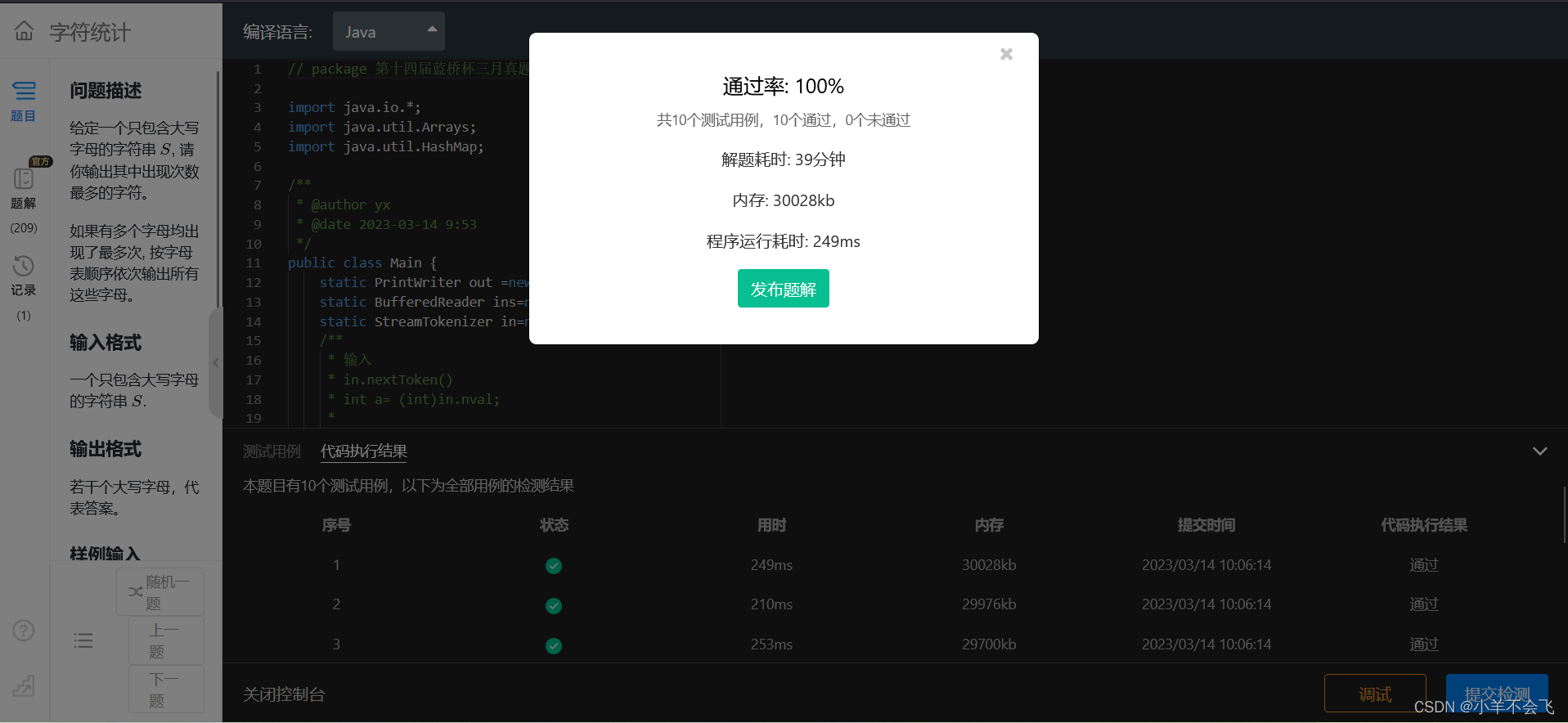
第十四届蓝桥杯三月真题刷题训练——第 11 天
目录 第 1 题:卡片 题目描述 运行限制 第 2 题:路径_dpgcd 运行限制 第 3 题:字符统计 问题描述 输入格式 输出格式 样例输入 样例输出 评测用例规模与约定 运行限制 第 4 题:费用报销 第 1 题:卡片 题…...
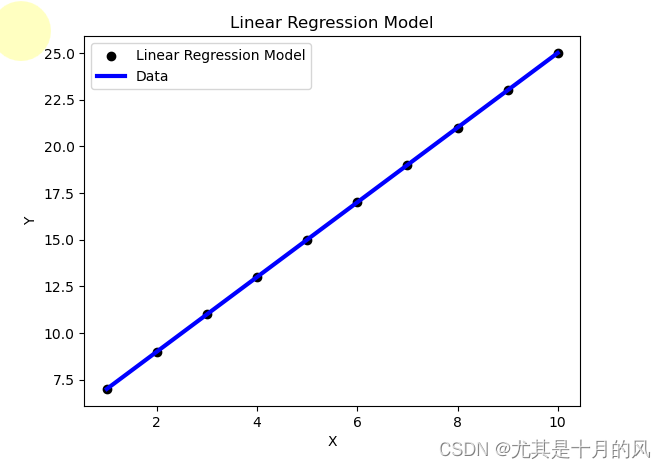
机器学习入门——线性回归
线性回归什么是线性回归?回归分析:线性回归:回归问题求解单因子线性回归简单实例评估模型表现可视化模型展示多因子线性回归什么是线性回归? 回归分析: 根据数据,确定两种或两种以上变量间相互依赖的定量…...
)
Microsoft Word 远程代码执行漏洞(CVE-2023-21716)
本文转载于: https://mp.weixin.qq.com/s?__bizMzI5NTUzNzY3Ng&mid2247485476&idx1&sneee5c7fd1c4855be6441b8933b10051e&chksmec535547db24dc516d013d3d76097e985aaad7f10f82f15b4e355a97af75fd333acdab6232af&mpshare1&scene23&srci…...
SharedPreferences存储及测试)
Android kotlin 系列讲解(数据篇)SharedPreferences存储及测试
文章目录 一、什么是SharedPreferences1、将数据存储到SharedPreferences中2、从SharedPreferences中读取数据二、登录使用SharedPreferences一、什么是SharedPreferences SharedPreferences是使用键值对的方式来存储数据的。也就是说,当保存一条数据的时候,需要给这条数据提…...
一文了解Web Worker
一、概述 众所周知,JavaScript最初设计是运行在浏览器中的,为了防止多个线程同时操作DOM带来的渲染冲突问题,所以JavaScript执行器被设计成单线程。但是随着前端技术的发展,JavaScript要处理的工作也越来越复杂,当我们…...
接口文档包含哪些内容?怎么才能写好接口文档?十年测试老司机来告诉你
目录 接口文档结构 参数说明 示例 错误码说明 语言基调通俗易懂 及时更新与维护 总结 那么我们该如何写好一份优秀的接口文档呢? 接口文档结构 首先我们要知道文档结构是什么样子的。接口文档应该有清晰明确的结构,以便开发人员能快速定位自己需…...
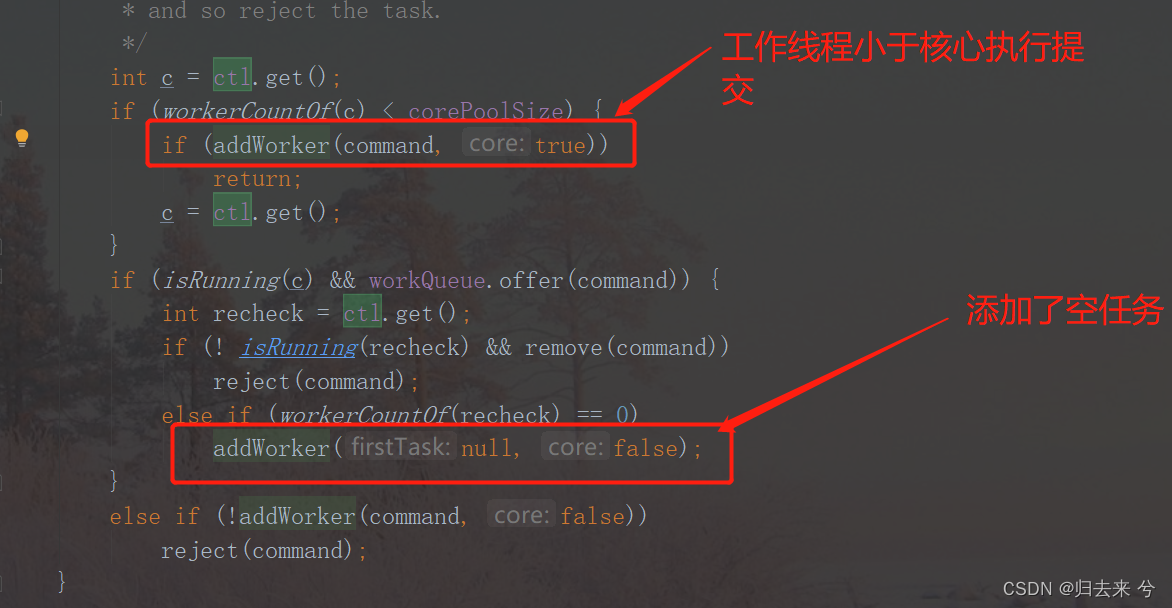
java面试八股文之------Java并发夺命23问
java面试八股文之------Java并发夺命23问👨🎓1.java中线程的真正实现方式👨🎓2.java中线程的真正状态👨🎓3.如何正确停止线程👨🎓4.java中sleep和wait的区别👨…...

CANoe中使用CAPL刷写流程详解(Trace图解)(CAN总线)
🍅 我是蚂蚁小兵,专注于车载诊断领域,尤其擅长于对CANoe工具的使用🍅 寻找组织 ,答疑解惑,摸鱼聊天,博客源码,点击加入👉【相亲相爱一家人】🍅 玩转CANoe&…...

【MySQL】002 -- 日志系统:一条SQL更新语句是如何执行的
此文章为《MySQL 实战 45 讲》的学习笔记,其课程链接可参见:MySQL实战45讲_MySQL_数据库-极客时间 目录 一、日志系统 1、重做日志:redo log(引擎层) 2、归档日记:binlog(Server层) …...
)
C++---背包模型---数字组合(每日一道算法2023.3.14)
注意事项: 本题是"动态规划—01背包"的扩展题,优化思路不多赘述,dp思路会稍有不同,下面详细讲解。 题目: 给定 N个正整数 A1,A2,…,AN,从中选出若干个数,使它们的和为 M,…...
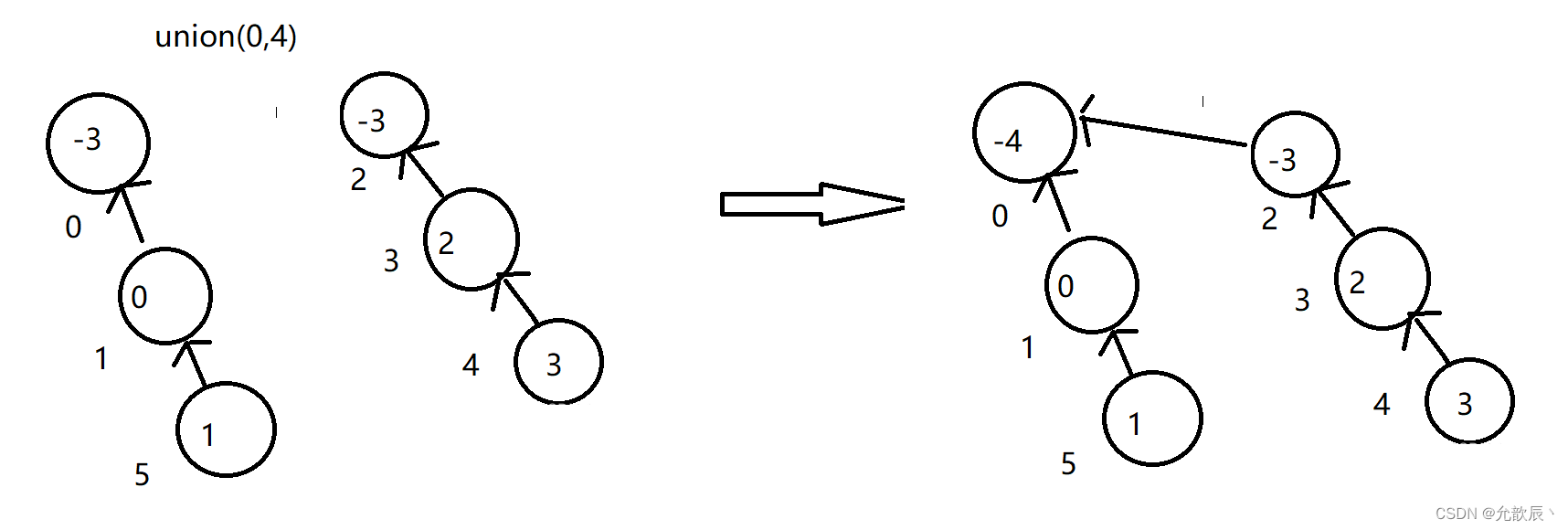
并查集(不相交集)详解
目录 一.并查集 1.什么是并查集 2.并查集的基本操作 3.并查集的应用 4.力扣上的题目 二.三大操作 1.初始化 2.查找 3.合并 三.省份数量 1.题目描述 2.问题分析 3.代码实现 四.冗余连接 1.题目描述 2.问题分析 3.代码实现 一.并查集 1.什么是并查集 并查集&…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
