「ML 实践篇」分类系统:图片数字识别
目的:使用 MNIST 数据集,建立数字图像识别模型,识别任意图像中的数字;
文章目录
- 1. 数据准备(MNIST)
- 2. 二元分类器(SGD)
- 3. 性能测试
- 1. 交叉验证
- 2. 混淆矩阵
- 3. 查准率与查全率
- 4. P-R 曲线
- 5. ROC 曲线
- 6. RandomForestClassifier vs. SGDClassifier
- 4. 多类分类器
- 5. 误差分析
- 6. 多标签分类
- 7. 多输出分类
- 1. 消除图片中的噪声
1. 数据准备(MNIST)
MNIST,一组由美国高中生和人口调查局员工手写的 70000 个数字图片;每张图片都用其代表的数字标记;因广泛被应用于机器学习入门,被称作机器学习领域的Hello World;也可用于测试新分类算法的效果;
使用 Scikit-Learn 下载数据集的前置工作
import ssl
ssl._create_default_https_context = ssl._create_unverified_context
Scikit-Learn 使用 Python 的 urllib 包通过 HTTPS 协议下载数据集,这里全局取消证书验证(否则 Scikit-Learn 可能无法建立 ssl 连接);
使用 Scikit-Learn 下载 MNIST
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1)
mnist.keys()dict_keys(['data', 'target', 'frame', 'categories', 'feature_names', 'target_names', 'DESCR', 'details', 'url'])### 查看数组
X, y = mnist["data"], mnist["target"]
X.shape(70000, 784)y.shape
(70000,)
共 70000 张图片,每张图片由 784 个特征(28 * 28 个像素,每个像素用 0(白色) 到 255(黑色) 表示);
Scikit-Learn 数据集通用字典结构
DESCR,描述数据集;data,包含一个数组,每个实例为一行,每个特征为一列;target,包含一个带有标记的数组;
使用 Matplotlib 查看数字图片
- 编写绘图函数;
import matplotlib.pyplot as plt
import matplotlib as mpldef plot_digit(data):image = data.reshape(28, 28)plt.imshow(image, cmap = mpl.cm.binary, interpolation="nearest")plt.axis("off")def plot_digits(instances, images_per_row=10, **options):size = 28images_per_row = min(len(instances), images_per_row)# This is equivalent to n_rows = ceil(len(instances) / images_per_row):n_rows = (len(instances) - 1) // images_per_row + 1# Append empty images to fill the end of the grid, if needed:n_empty = n_rows * images_per_row - len(instances)padded_instances = np.concatenate([instances, np.zeros((n_empty, size * size))], axis=0)# Reshape the array so it's organized as a grid containing 28×28 images:image_grid = padded_instances.reshape((n_rows, images_per_row, size, size))# Combine axes 0 and 2 (vertical image grid axis, and vertical image axis),# and axes 1 and 3 (horizontal axes). We first need to move the axes that we# want to combine next to each other, using transpose(), and only then we# can reshape:big_image = image_grid.transpose(0, 2, 1, 3).reshape(n_rows * size, images_per_row * size)# Now that we have a big image, we just need to show it:plt.imshow(big_image, cmap = mpl.cm.binary, **options)plt.axis("off")
- MNIST 的第一个图片展示;
some_digit = X[:1].to_numpy()
plot_digit(some_digit)
plt.show()

# 查看图片对应标签,验证是一个数字 '5'
y[0]'5'
- MNIST 的多图样例展示;
plt.figure(figsize=(9,9))
example_images = X[:100]
plot_digits(example_images, images_per_row=10)
# save_fig("more_digits_plot")
plt.show()

将字符标签转换成整数
import numpy as npy = y.astype(np.uint8)
创建测试集
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
MNIST 数据集已经分成训练集(前 6 万张图片)和测试集(最后 1 万张图片);
可以对训练集进行混洗,保障在做交叉验证时所有折叠的实例分布相当;有一些算法对训练实例的顺序敏感,连续输入相同的实例可能导致性能不佳;也有一些情况时间序列也是实例特征(如股市架构或天气状态),则不可混洗数据集;
2. 二元分类器(SGD)
二元分类器,在两个类中区分;
简化问题,图片数字识别,先从识别图片 是 5 和 非 5 开始;
转换图片的标签
y_train_5 = (y_train == 5) # True for all 5s, False for all other digits
y_test_5 = (y_test == 5)
使用 Scikit-Learn 的 SGDClassifier 训练随机梯度下降(SGD)分类器
SGD,独立处理训练实例,一次一个,非常适合处理大型的数据集,也适合在线学习;
from sklearn.linear_model import SGDClassifiersgd_clf = SGDClassifier(random_state=42)
sgd_clf.fit(X_train, y_train_5)
给 random_state 设置固定值,如 =42 可以让 SGD 的随机训练变得结果可复现;
sgd_clf.predict(X[:1])array([ True])
SGD 分类器预测这是一张 5,结果正确;
3. 性能测试
准确率,正确预测的比率;
1. 交叉验证
自定义实现交叉验证
from sklearn.model_selection import StratifiedKFold
from sklearn.base import cloneskfolds = StratifiedKFold(n_splits=3, random_state=42, shuffle=True)for train_index, test_index in skfolds.split(X_train, y_train_5):clone_clf = clone(sgd_clf)X_train_folds = X_train.iloc[train_index]y_train_folds = y_train_5.iloc[train_index]X_test_fold = X_train.iloc[test_index]y_test_fold = y_train_5.iloc[test_index]clone_clf.fit(X_train_folds, y_train_folds)y_pred = clone_clf.predict(X_test_fold)n_correct = sum(y_pred == y_test_fold)print(n_correct / len(y_pred))0.9669
0.91625
0.96785
StratifiedKFold,实现分层抽样;让每个折叠中各个类的比例与整体比例相当;clone,为每个迭代创建一个分类器的副本,用于对训练集的训练和测试集的预测;
使用 Scikit-Learn 的 cross_val_score() 实现 K-折交叉验证
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")array([0.95035, 0.96035, 0.9604 ])
K-折交叉验证,将训练集分解成 K 个折叠(这里是 3 折),每次留 1 个折叠用于测试集,剩余用于训练集;
所有折叠交叉验证的准确率都超过了 91%,这看似很准确,实则准确率不足以衡量这个分类器的优劣;
自定义 非 5 分类器
from sklearn.base import BaseEstimatorclass Never5Classifier(BaseEstimator):def fit(self, X, y=None):return selfdef predict(self, X):return np.zeros((len(X), 1), dtype=bool)never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train, y_train_5, cv=3, scoring="accuracy")array([0.91125, 0.90855, 0.90915])
使用自定义 非 5 分类器进行交叉验证,得到所有折叠的准确率也在 90% 以上;这是因为所有图片中只有约 10% 是数字 5,90% 非 5 是正确的;这进一步说明准确率不足以评判分类器的性能(特别是处理有偏数据集时);
2. 混淆矩阵
-
混淆矩阵,对多个二分类或多分类进行训练/测试,统计 A 类实例被分类为 B 类别的次数;是评估分类器性能的常见方法; -
使用 cross_val_predict() 进行 K-折交叉预测
from sklearn.model_selection import cross_val_predicty_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
cross_val_predict 与 cross_val_score 类似,但返回的不是交叉验证的评分,而是每个折叠的预测值;
- 使用 confusion_matrix() 获取混淆矩阵
from sklearn.metrics import confusion_matrixconfusion_matrix(y_train_5, y_train_pred)array([[53892, 687],[ 1891, 3530]])
混淆矩阵的行表示实际类别(实际为 非 5、5),列表示预测类别(预测为 非 5、5);
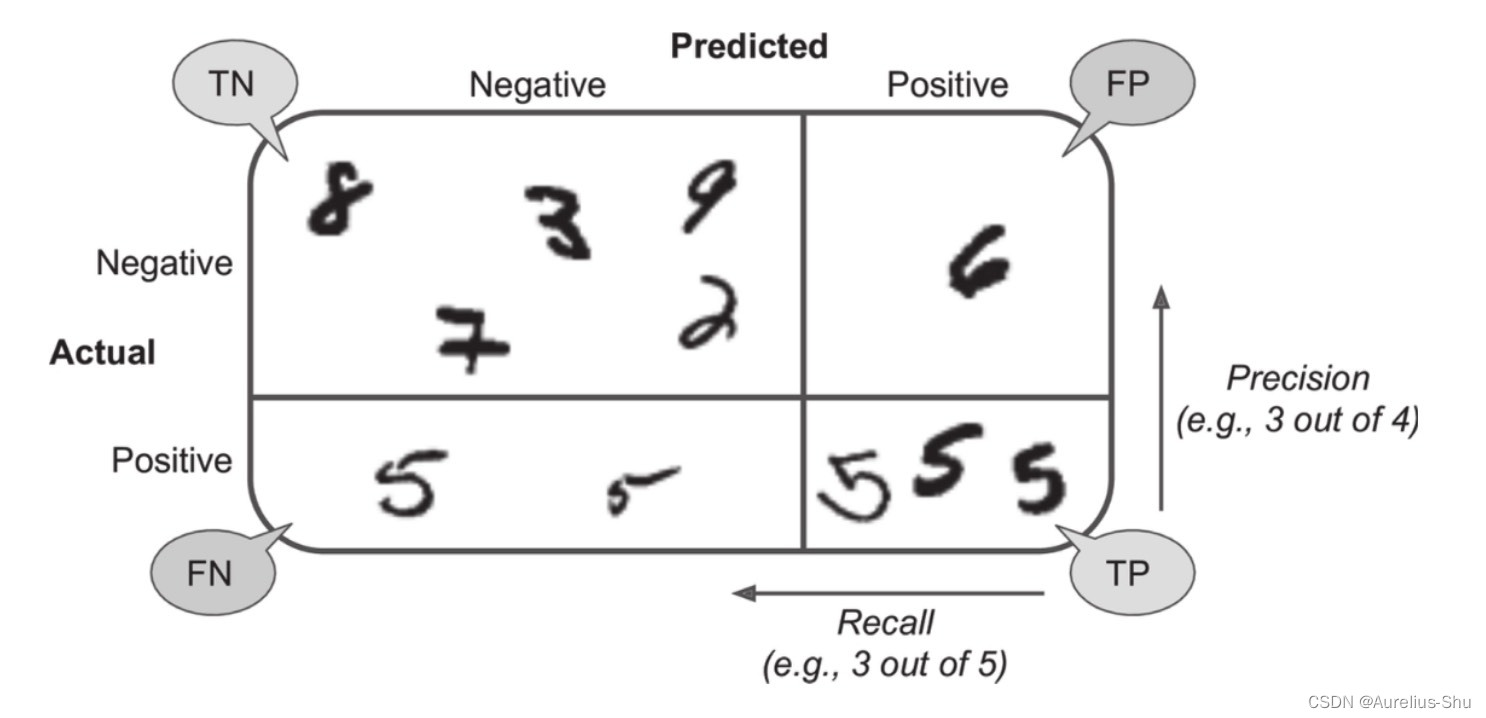
负类(Negative):实际为非 5真负类(TN):53892 个正确分类为非 5;假正类(FP):687 个错误分类为5;
正类(Positive):实际为5假负类(FN):1891 个错误分类为非 5;真正类(TP):3530 个正确分类为5;
完美的分类器只存在真正类与真负类,混淆矩阵的对角线(左上和右下)有非零值;
y_train_perfect_predictions = y_train_5 # pretend we reached perfection
confusion_matrix(y_train_5, y_train_perfect_predictions)array([[54579, 0],[ 0, 5421]])
3. 查准率与查全率
查准率(precision),真正类占真正类和假正类之和的比例;将忽略这个正类实例之外的所有内容;
precision=TPTP+FPprecision = \frac{TP}{TP + FP} precision=TP+FPTP
查全率(recall):召回率,灵敏度或真正类率,真正类占所有正类(真正类和假负类)之和的比例;正确检测到的正类实例的比率;
recall=TPTP+FNrecall = \frac{TP}{TP + FN} recall=TP+FNTP
使用 Scikit-Learn 计算查准率和查全率
from sklearn.metrics import precision_score, recall_scoreprecision_score(y_train_5, y_train_pred) # == 3530 / (3530 + 687)0.8370879772350012recall_score(y_train_5, y_train_pred) # == 3530 / (3530 + 1891)0.6511713705958311
这说明,当这个 5-检测器 说一张图片是 5 时,只有 83% 时准确的,且只有 65% 的 5 被检测出来了;
- F1F_1F1 分数,查准率与查全率的谐波平均值,会给予低值更高的权重;更适用于查准率和查全率相近的分类器;
F1=21precision+1recall=2×precision×recallprecision+recall=TPTP=FN+FP2F_1 = \frac{2}{\frac{1}{precision} + \frac{1}{recall}} = 2 \times \frac{precision \times recall}{precision + recall} = \frac{TP}{TP = \frac{FN + FP}{2}} F1=precision1+recall12=2×precision+recallprecision×recall=TP=2FN+FPTP
使用 f1_score() 计算 F1F_1F1 分数
from sklearn.metrics import f1_scoref1_score(y_train_5, y_train_pred)0.7325171197343846
鱼与熊掌不可得兼,不能同时兼顾查准率和查全率;
-
对于
宁缺毋滥类型的分类器,更在乎查准率(如给小孩子推荐视频); -
对于
宁杀错不放过类型的分类器,更在乎查全率(如小区监控抓小偷);
4. P-R 曲线
P-R 曲线,将实例按预测为正类的概率高低排序,然后逐个把样本作为正类进行预测评估,计算其查准率和查全率,以查全率为横轴,查准率为纵轴绘制一个曲线图;
SGDClassifier 的分类决策
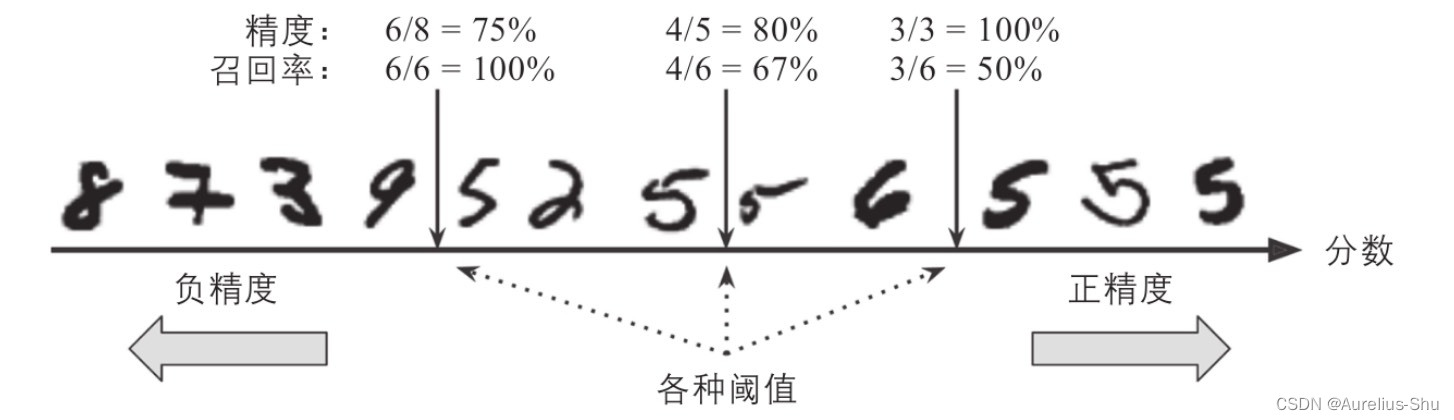
基于决策函数计算处每个实例的分值;将每个实例按分数从低到高从左到右排列;取一个阈值,大于该阈值的实例为正类,否则为负类;(通常阈值越高,查全率越低,查准率越高);
- 若决策阈值在中间箭头位置(两个 5 之间),查准率为 80%(4/5),查全率为 67%(4/6);
- 若决策阈值在右边箭头位置(提升阈值),查准率为 100%(3/3),查全率为 50%(3/6);
- 若决策阈值在左边箭头位置(降低阈值),查准率为 75%(6/8),查全率为 100%(6/6);
使用 decision_function() 获取每个实例的分数
y_scores = sgd_clf.decision_function(some_digit)
y_scoresarray([2164.22030239])
- 通过阈值控制预测结果;
threshold = 0
y_some_digit_pred = (y_scores > threshold)
y_some_digit_predarray([ True])
- 提升阈值控制预测结果;
threshold = 8000
y_some_digit_pred = (y_scores > threshold)
y_some_digit_predarray([False])
提升阈值可以降低查全率(将本是 5 的图片判定为了非 5);
使用 cross_val_predict() 获取训练集的实例分数
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3, method="decision_function")
使用 precision_recall_curve() 计算所有阈值对应的查准率和查全率
from sklearn.metrics import precision_recall_curveprecisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
绘制查准率和查全率与决策阈值的关系曲线
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)plt.legend(loc="center right", fontsize=16)plt.xlabel("Threshold", fontsize=16)plt.grid(True)plt.axis([-50000, 50000, 0, 1])recall_90_precision = recalls[np.argmax(precisions >= 0.90)]
threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]plt.figure(figsize=(8, 4))
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.plot([threshold_90_precision, threshold_90_precision], [0., 0.9], "r:")
plt.plot([-50000, threshold_90_precision], [0.9, 0.9], "r:")
plt.plot([-50000, threshold_90_precision], [recall_90_precision, recall_90_precision], "r:")
plt.plot([threshold_90_precision], [0.9], "ro")
plt.plot([threshold_90_precision], [recall_90_precision], "ro")
plt.show()
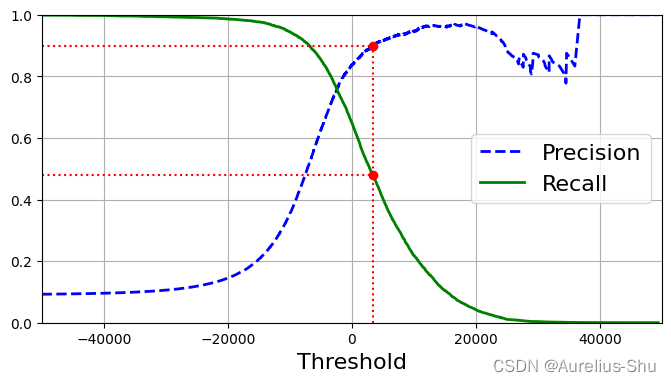
查准率比查全率曲线要崎岖一些,因为随着阈值的提升,查准率可能会下降,但查全率只会下降;
绘制 P/R 曲线
以查全率为横轴,查准率为纵轴,将上文决策阈值关系图转化成一张 P-R 曲线;
def plot_precision_vs_recall(precisions, recalls):plt.plot(recalls, precisions, "b-", linewidth=2)plt.xlabel("Recall", fontsize=16)plt.ylabel("Precision", fontsize=16)plt.axis([0, 1, 0, 1])plt.grid(True)plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
plt.plot([recall_90_precision, recall_90_precision], [0., 0.9], "r:")
plt.plot([0.0, recall_90_precision], [0.9, 0.9], "r:")
plt.plot([recall_90_precision], [0.9], "ro")
plt.show()
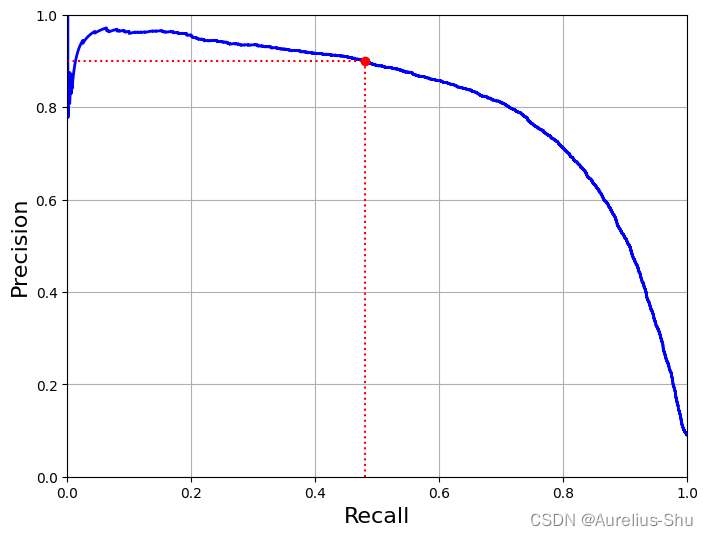
查全率在 80% 之后,查准率急剧下降,说明可能需要在此之前选择一个权衡点;
通常若学习器 A 的 P-R 曲线能完全包住学习器 B 的,则可断言 A 优于 B;若存在交叉,可采用面积比较法,或平衡点比较法;
查找指定查准率/查全率的最低/最高阈值
>>> threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]
3370.0194991439557 # 第一个 True 的最大索引>>> threshold_90_recall = thresholds[np.argmin(recalls >= 0.90)]
-6861.032537940274 # 第一个 True 的最小索引
使用实例分数与阈值进行预测
>>> y_train_pred_90 = (y_scores >= threshold_90_precision)array([False, False, False, ..., True, False, False])
- 查看预测的查准率与查全率;
>>> precision_score(y_train_5, y_train_pred_90)
0.9000345901072293>>> recall_score(y_train_5, y_train_pred_90)
0.4799852425751706
查准率确实是指定的 90%;
5. ROC 曲线
-
ROC(Receiver Operating Characteristic,受试者工作特征),以真正类率为纵轴,以假正类率为横轴;描述的是查全率与(1 - 特异度)的关系;与 P-R 图相似,若学习器 A 的曲线完全包住学习器 B 的曲线,则可可断言 A 优于 B; -
真正类率,查全率、灵敏度、召回率、True Positive Rate,TPR= TPTP+FN\frac{TP}{TP + FN}TP+FNTP,所有正类中被测出来的正类的概率; -
假正类率,False Positive Rate,FPR= FPTN+FP\frac{FP}{TN + FP}TN+FPFP,所有负类中被错认为正类的概率; -
真负类率,TNR,特异率,正确被分类为负类的负类实例比率;
使用 roc_curve() 计算多种阈值的 TPR 和 FPR
from sklearn.metrics import roc_curvefpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
通过 Matplotlib 绘制 ROC 曲线
def plot_roc_curve(fpr, tpr, label=None):plt.plot(fpr, tpr, linewidth=2, label=label)plt.plot([0, 1], [0, 1], 'k--') # dashed diagonalplt.axis([0, 1, 0, 1])plt.xlabel('False Positive Rate (Fall-Out)', fontsize=16)plt.ylabel('True Positive Rate (Recall)', fontsize=16)plt.grid(True)plt.figure(figsize=(8, 6))
plot_roc_curve(fpr, tpr)
fpr_90 = fpr[np.argmax(tpr >= recall_90_precision)]
plt.plot([fpr_90, fpr_90], [0., recall_90_precision], "r:")
plt.plot([0.0, fpr_90], [recall_90_precision, recall_90_precision], "r:")
plt.plot([fpr_90], [recall_90_precision], "ro")
plt.show()
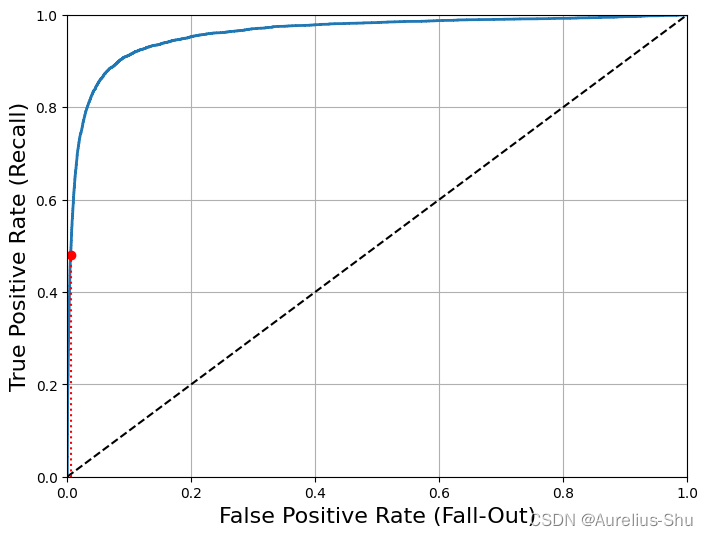
召回率(TPR)越高,分类器的假正类(FPR)就越多(虚线表示纯随机分类器的 ROC 曲线,越高于虚线的 ROC 曲线,对应的分类器越优);
使用 Scikit-Learn 计算 ROC 的 AUC
AUC,Area Under ROC Curve,ROC 曲线下的面积;当 ROC 曲线相交时,可通过 AUC 判定学习器的好坏;
from sklearn.metrics import roc_auc_score>>> roc_auc_score(y_train_5, y_scores)
0.9604938554008616
这里 ROC AUC 分值看着很高,是因为正类(数字 5)比负类(非 5)的数量少很多;
P-R 曲线与 ROC 曲线的选择
当正类非常少见或者更关注假正类而非假负类是,选择 P-R 曲线;反之选择 ROC 曲线;
6. RandomForestClassifier vs. SGDClassifier
RandomForestClassifier 没有 decision_function(),代替的是 dict_proba();
dict_proba(),返回一个数组,每行代表一个实例,每列表示一个类别,代表某个实例属于某个给定类别的概率;
训练 RandomForestClassifier 分类器
from sklearn.ensemble import RandomForestClassifierforest_clf = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3, method="predict_proba")y_scores_forest = y_probas_forest[:, 1] # score = proba of positive class
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5, y_scores_forest)
这里将正类率作为分数传递给 roc_curve();
绘制 RandomForestClassifier 分类器的 ROC 曲线
plt.plot(fpr, tpr, "b:", label="SGD")
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
plt.legend(loc="lower right")
plt.show()
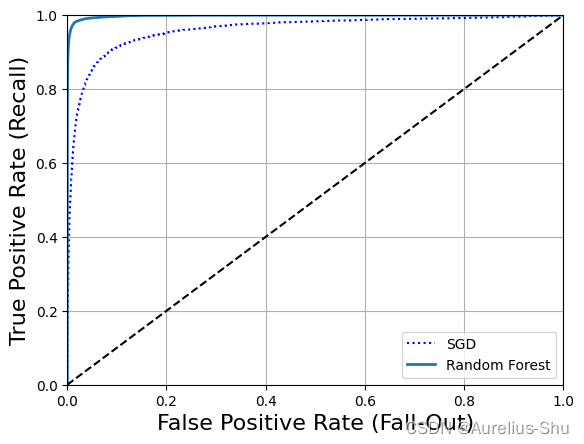
RandomForestClassifier 的 ROC 曲线比 SGDClassifier 好很多;
# ROC AUC 分数
>>> roc_auc_score(y_train_5, y_scores_forest)
0.9983436731328145# 查准率
y_train_pred_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3)
>>> precision_score(y_train_5, y_train_pred_forest)
0.9905083315756169# 查全率(召回率)
>>> recall_score(y_train_5, y_train_pred_forest)
0.8662608374838591
RandomForestClassifier 的效果确实好很多(查准率与查全率都比较高);
4. 多类分类器
多元分类器,多项分类器,在两个以上的类别中区分;
随机森林、朴素贝叶斯等分类器可以直接处理多个类;支持向量机、线性分类器则是严格的二元分类器,但是可以通过一些策略让二院分类器实现多分类的目的;
OvR,一对剩余,一对多(one-versus-all),训练 10 个二元分类器(0-检测器、1-检测器、2-检测器…),当需要检测一张图片时,先获取每个分类器的决策分数,哪个分类器的分值最高,图片归为哪一类;OvO,一对一,训练 N×(N−1)2\frac{N \times (N - 1)}{2}2N×(N−1) 个分类器,为每一对数字训练一个二元分类器(0-1 分类器、0-2 分类器、1-2 分类器…);优点是,每个分类器只需要用到部分训练集对其必须区分的两个类进行训练;
支持向量机在数据规模较大时表现较差,因此应优先选择 OvO 策略,但对于大多数二分类器来书,OvR 是更好的选择;
使用 Scikit-Learn 训练 SVM 分类器
>>> from sklearn.svm import SVC
>>> svm_clf = SVC()
>>> svm_clf.fit(X_train, y_train) # y_train, not y_train_5
>>> svm_clf.predict([some_digit])
array([5], dtype=uint8)
Scikit-Learn 检测到尝试使用二元分类算法进行多类分类任务时,会自动运行 OvR 或 OvO;
这里 Scikit-Learn 实际训练了 45 个二元分类器,获得它们对图片的决策分数,然后选择了分数最高的类;
使用 decision_function() 查看 SVM 分类器的分数
>>> some_digit_scores = svm_clf.decision_function(some_digit)
>>> some_digit_scores
array([[ 1.72501977, 2.72809088, 7.2510018 , 8.3076379 , -0.31087254,9.3132482 , 1.70975103, 2.76765202, 6.23049537, 4.84771048]])
查看分数最高的分类
>>> np.argmax(some_digit_scores)
5
>>> svm_clf.classes_
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8)
>>> svm_clf.classes_[5]
5
classes_,存储目标类的列表,按值的大小排序(索引与类值不一定相同);
强制使用 OneVsRestClassifier 策略训练 SVC 多类分类器
>>> from sklearn.multiclass import OneVsRestClassifier
>>> ovr_clf = OneVsRestClassifier(SVC())
>>> ovr_clf.fit(X_train, y_train)
>>> ovr_clf.predict(some_digit)
array([5], dtype=uint8)
>>> len(ovr_clf.estimators_)
10
OneVsRestClassifier,OvR 策略实现类;OneVsOneClassifier,OvO 策略实现类;
训练 SGDClassifier 的多类分类器
>>> sgd_clf.fit(X_train, y_train)
>>> sgd_clf.predict([some_digit])
array([3], dtype=uint8)
SGC 分类器可以直接将实例分为多个类,不必运行 OvR 或 OvO;
使用 decision_function() 计算每个实例分类为每个类的概率
>>> sgd_clf.decision_function(some_digit)
array([[-31893.03095419, -34419.69069632, -9530.63950739,1823.73154031, -22320.14822878, -1385.80478895,-26188.91070951, -16147.51323997, -4604.35491274,-12050.767298 ]])
第 3 类得分 1823,其他都是负分值(预测错误,实际是 5);
使用 scross_val_score() 评估 SGDClassifier 的准确性
>>> cross_val_score(sgd_clf, X_train, y_train, cv=3, scoring="accuracy")
array([0.87365, 0.85835, 0.8689 ])
每个折叠的准确率在 85% 以上(随机分类器准确率约为 10%);
通过缩放对 SGD 分离进行优化
>>> from sklearn.preprocessing import StandardScaler
>>> scaler = StandardScaler()
>>> X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
>>> cross_val_score(sgd_clf, X_train_scaled, y_train, cv=3, scoring="accuracy")
array([0.8983, 0.891 , 0.9018])
简单缩放训练集数据后,准确率提升到 89%;
5. 误差分析
使用 cross_val_predict() 进行预测并计算混淆矩阵
>>> y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
>>> conf_mx = confusion_matrix(y_train, y_train_pred)
>>> conf_mx
array([[5577, 0, 22, 5, 8, 43, 36, 6, 225, 1],[ 0, 6400, 37, 24, 4, 44, 4, 7, 212, 10],[ 27, 27, 5220, 92, 73, 27, 67, 36, 378, 11],[ 22, 17, 117, 5227, 2, 203, 27, 40, 403, 73],[ 12, 14, 41, 9, 5182, 12, 34, 27, 347, 164],[ 27, 15, 30, 168, 53, 4444, 75, 14, 535, 60],[ 30, 15, 42, 3, 44, 97, 5552, 3, 131, 1],[ 21, 10, 51, 30, 49, 12, 3, 5684, 195, 210],[ 17, 63, 48, 86, 3, 126, 25, 10, 5429, 44],[ 25, 18, 30, 64, 118, 36, 1, 179, 371, 5107]])
使用 Matplotlib 的 matshow() 查看混淆矩阵
plt.matshow(conf_mx, cmap=plt.cm.gray)
plt.show()
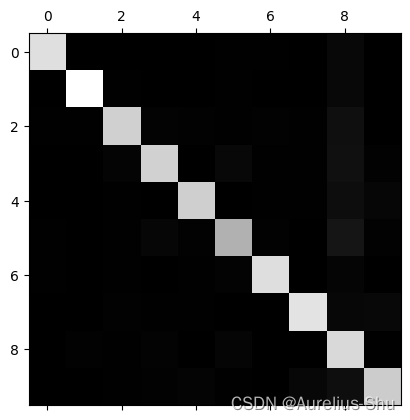
大多数图片被分到对角线上,说明它们被正确分类了;数字 5 略暗,说明可能数字 5 较少,也可能数字 5 的分类效果不如其他数字;
将混淆矩阵中的每个值除以相应类中的图片数量,这样比较的就是错误率(而非错误的绝对值)
row_sums = conf_mx.sum(axis=1, keepdims=True)
norm_conf_mx = conf_mx / row_sums
重新绘制混淆矩阵效果图
用 0 填充对角线,只看错误部分;
np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx, cmap=plt.cm.gray)
plt.show()
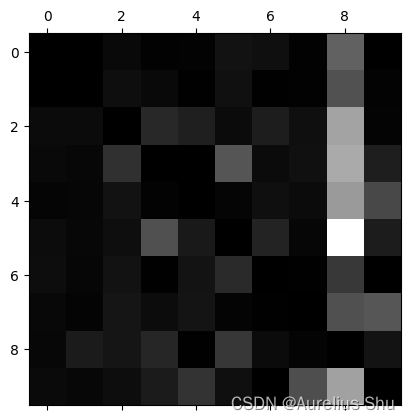
每行代表实际类、每列代表预测类;
- 第 8 列比较亮,说明许多图片被错误的分类为了 8;
- 改进数字 8 的分类错误,可以试着收集更多像数字 8 的训练数据,以便分类器学会将它们与真实的数字 8 区分开;也可以开发一些新特征用来改进分类器(计算闭环的数量,如 8 有两个、6 有一个、5 没有);还可以对图片进行预处理(Scikit-Image、Pillow、OpenCV 等),让某些模式更为突出,如闭环等;
- 数字 3 和数字 5 经常被混淆,两个方向的交叉处较亮;
- 可以分析单个错误示例在做什么,为何失败;
查看数字 3 和数字 5
cl_a, cl_b = 3, 5
X_aa = X_train[(y_train == cl_a) & (y_train_pred == cl_a)]
X_ab = X_train[(y_train == cl_a) & (y_train_pred == cl_b)]
X_ba = X_train[(y_train == cl_b) & (y_train_pred == cl_a)]
X_bb = X_train[(y_train == cl_b) & (y_train_pred == cl_b)]
plt.figure(figsize=(8,8))
plt.subplot(221); plot_digits(X_aa[:25], images_per_row=5)
plt.subplot(222); plot_digits(X_ab[:25], images_per_row=5)
plt.subplot(223); plot_digits(X_ba[:25], images_per_row=5)
plt.subplot(224); plot_digits(X_bb[:25], images_per_row=5)
plt.show()

左侧两个 5×55 \times 55×5 矩阵显示了呗分类为数字 3 的图片,右侧两个 5×55 \times 55×5 矩阵显示了被分类为数字 5 的图片(左下和右上为分类错误示例);
SGD 是一个简单的线性模型,它为每一个像素分配一个各个类别的权重,当它看到新图片时,将加权后的 像素强度汇总,从而得到一个分数进行分类;而 3 和 5 的像素位大多重叠,因此容易混淆;
减少 3 和 5 之间混淆的方式可以是对图片进行预处理,如确保他们在中心位置且没有选择;
6. 多标签分类
多标签分类,分类器为每个实例输出多个类(如一张图片识别出多个人);
使用 KNeighborsClassifier 创建多标签分类
KNeighborsClassifier,支持多标签分类,不是所有分类器都支持;
>>> from sklearn.neighbors import KNeighborsClassifier
>>> y_train_large = (y_train >= 7) # 大数标签
>>> y_train_odd = (y_train % 2 == 1) # 奇数标签
>>> y_multilabel = np.c_[y_train_large, y_train_odd] # 多标签数组
>>> knn_clf = KNeighborsClassifier()
>>> knn_clf.fit(X_train, y_multilabel)
>>> knn_clf.predict(some_digit)
array([[False, True]])
分类正确:数字 5 不是大数,是奇数;
多标签分类器的性能评估
>>> y_train_knn_pred = cross_val_predict(knn_clf, X_train, y_multilabel, cv=3)
>>> f1_score(y_multilabel, y_train_knn_pred, average="macro")
0.976410265560605
假设所有标签都同等重要,可以通过测量每个标签的 F1F_1F1 分数(或其他任何二元分类器指标),并计算它们的平均分数;
但实际往往并发如此,比如识别图片中的多个人,其中有的人可能拍了很多照片,那这个人的权重就要高很多;这时需要给每个标签设置一个相当的权重(可以是具有该目标标签的实例的数量);
7. 多输出分类
多输出分类,或称多输出多分类,是多标签分类的泛化,其标签也可以是多类的;
1. 消除图片中的噪声
目标:构建一个系统,输入一张有噪声的图片,系统输出一张干净的数字图片;
分类和回归之间有时是模糊的,这个示例即可一说是多输出分类任务,也可以说是像素强度的回归任务;
使用 NumPy 的 randint() 为 MNIST 图片添加噪声
noise = np.random.randint(0, 100, (len(X_train), 784))
X_train_mod = X_train + noise
noise = np.random.randint(0, 100, (len(X_test), 784))
X_test_mod = X_test + noise
y_train_mod = X_train
y_test_mod = X_test
查看图片样例
plt.subplot(121)
plot_digit(X_test_mod[:1].to_numpy())
plt.subplot(122)
plot_digit(y_test_mod[:1].to_numpy())
plt.show()
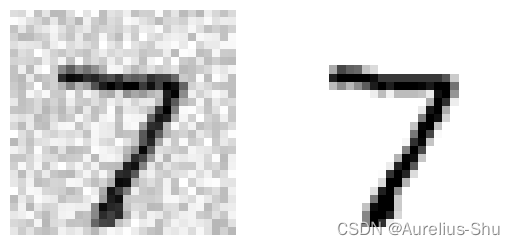
通过训练分类器,清洗噪声图片
knn_clf.fit(X_train_mod, y_train_mod)
clean_digit = knn_clf.predict(X_test_mod[:1].to_numpy())
plot_digit(clean_digit)

清洗后的效果与原图相近了!
- 上一篇:「ML 实践篇」回归系统:房价中位数预测
- 专栏:《机器学习》
PS:欢迎各路道友阅读与评论,感谢道友点赞、关注、收藏!
参考资料:
- [1]《机器学习》
- [2]《机器学习实战》
相关文章:

「ML 实践篇」分类系统:图片数字识别
目的:使用 MNIST 数据集,建立数字图像识别模型,识别任意图像中的数字; 文章目录1. 数据准备(MNIST)2. 二元分类器(SGD)3. 性能测试1. 交叉验证2. 混淆矩阵3. 查准率与查全率4. P-R 曲…...

从大专到测开,上海某字母站大厂的面试题,岗位是测开(25K*16)
简单介绍一句,大专出身,三年经验。跳了四次槽,面试了无数次,现在把自己的面试经验整理出来分享给大家,堪称必杀技! 1,一切从实际出发,对实际工作进行适当修饰 2,不会的简…...

【面试题】Python软件工程师能力评估试题(一)
文章目录前言应试者需知(一)Python 语言基础能力评估1、理解问题并完成代码:2、阅读理解代码,并在空白处补充完整代码:3、编写一个装饰器:exposer4、阅读代码并在空白处补充完整代码:5、自行用P…...
)
Java八股文(Java多线程面试题)
并行和并发的区别?(1)并行是指两个或者多个事件在同一时刻发生;而并发是指两个或多个事件在同一时间间隔发生;(2)并行是在不同实体上的多个事件,并发是在同一实体上的多个事件&#…...
小程序当前页面如何分享别的页面内容呢?
需求分析 因为功能的需要分为两点 他需要调转转发,并且有首页转发点击button按钮进行转发邀请好友帮忙助力,如何做到一个页面多种转发 如何区分,是button转发还剩右上角三个点转发呢? 通过onShareAppMessage()这个函数的事件…...
编写Java哪个编译器好
现在能够编写Java代码的工具简直不要太多,各种各样五花八门,但目前效率最高的还是Intellij Idea。但这个工具对于完全零基础的小白来说,第一次用起来是比较复杂的,因为它的功能太多了。这就好比你要学开车,如果上来就给…...

第十六章 Java为什么使用序列化
为何要指定serialVersionUID的值如果不指定显示serialVersionUID的值,jvm在序列化时会自动生成一个serialVersionUID,跟属性一起序列化,再进行持久化或者网络传输,在反序列化时,jvm会根据属性自动生成一个新版的serial…...

28岁小公司程序员,无车无房不敢结婚,要不要转行?
大家好,这里是程序员晚枫,又来分享程序员的职场故事了~ 今天分享的这位朋友叫小青,我认识他2年多了。以前从事的是土木行业,2年前找我咨询转行程序员的学习路线和职业规划后,通过自学加入了一家创业公司,成…...

出道即封神的ChatGPT,现在怎么样了?
从互联网的普及到智能手机,都让广袤的世界触手而及,如今身在浪潮中的我们,已深知其力。前阵子爆火的ChatGPT,不少人保持观望态度。现如今,国内关于ChatGPT的各大社群讨论,似乎沉寂了不少,现在怎…...
【计算机视觉】CNN 可视化算法
文章目录一、CAM算法1.1 概述1.2 CAM算法介绍二、Grad-CAM算法2.1 概述2.2 Guided Backpropagation2.3 Occlusion Sensitivity2.4 Grad-CAM 整体结构和效果2.5 Grad-CAM 实现细节一、CAM算法 1.1 概述 本文介绍 2016 年提出的 CAM (Class Activation Mapping) 算法࿰…...

自动抓取服务器巡检、登录、执行命令记录+备份脚本
文章目录 引抓取【巡检日志】语言&时区设置语言设置时区巡检脚本执行效果抓取【登录信息】登录脚本登录脚本低版本的last命令执行效果抓取【history记录】说明配置history授权日志文件显示时间戳持久化到日志未配置history的配置过history的执行脚本执行脚本...
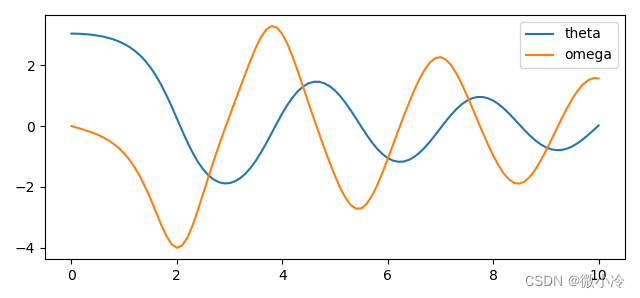
如何用Python求解微分方程组
文章目录odeint简介示例odeint简介 scipy文档中将odeint函数和ode, comples_ode这两个类称为旧API,是scipy早期使用的微分方程求解器,但由于是Fortran实现的,尽管使用起来并不方便,但速度没得说,所以有的时候还挺推荐…...

【微信小程序】-- 自定义组件 - behaviors(三十九)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

【微信小程序】-- 自定义组件 - 父子组件之间的通信(三十八)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &…...

Java Web 实战 11 - 多线程进阶之常见的锁策略
常见的锁策略常见的锁策略1. 乐观锁 VS 悲观锁2. 普通的互斥锁 VS 读写锁3. 重量级锁 VS 轻量级锁4. 自旋锁 VS 挂起等待锁5. 公平锁 VS 非公平锁6. 可重入锁 vs 不可重入锁7. 常见面试题大家好 , 这篇文章给大家带来的是多线程中常见的锁策略 , 我们会给大家讲解 6 种类别的锁…...
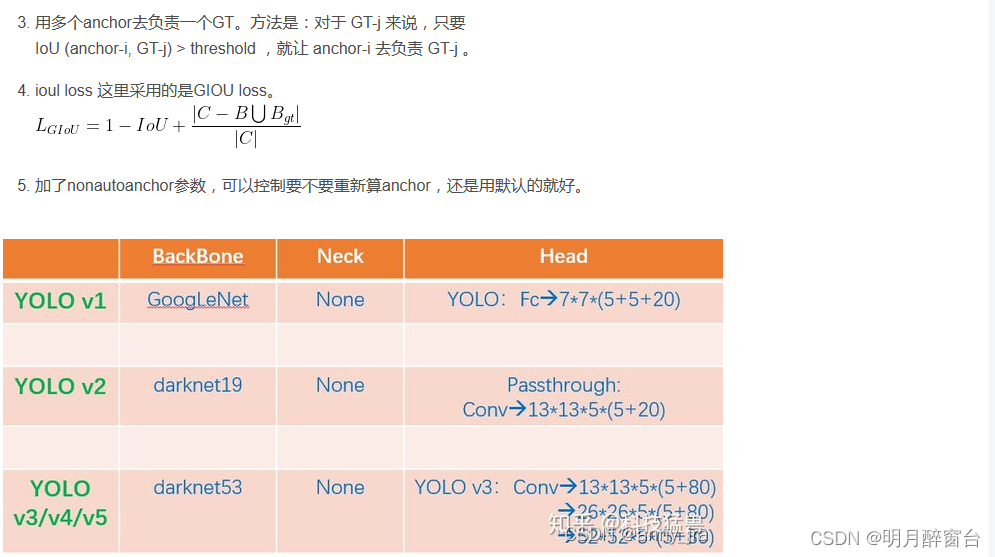
(20)目标检测算法之YOLOv5计算预选框、详解anchor计算
目标检测算法之YOLOv5计算预选框、详解anchor计算 单节段目标检测算法中:预选框的设定直接影响最终的检测精度众所周知,yolov5中采用自适应调整预选框anchor的大小,但万事开头难,配置文件config中的预设还是很重要yolo算法作为on…...
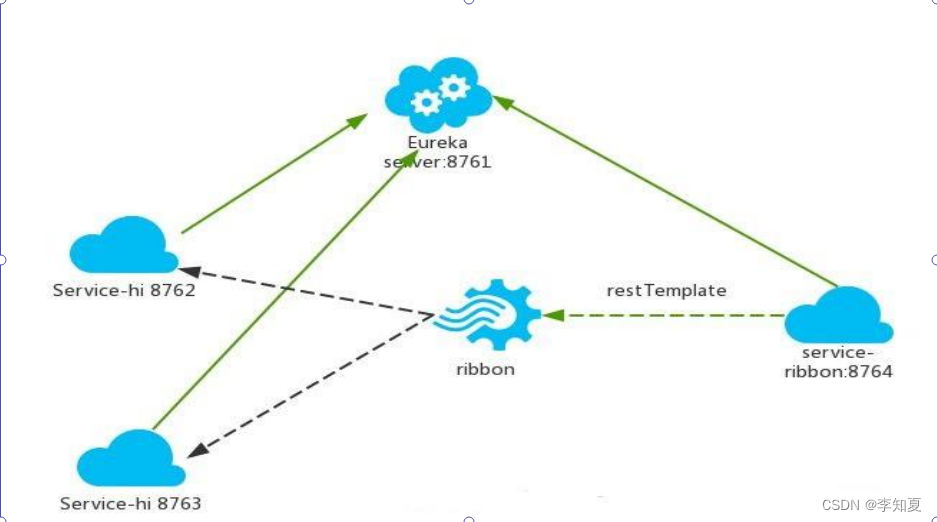
3-1 SpringCloud快速开发入门: Ribbon 是什么
接上一章节Eureka 服务注册中心自我保护机制,这里讲讲Ribbon 是什么 Ribbon 是什么 通常说的负载均衡是指将一个请求均匀地分摊到不同的节点单元上执行,负载均和分为硬件负载均衡和软件负载均衡: **硬件负载均衡:**比如 F5、深信…...
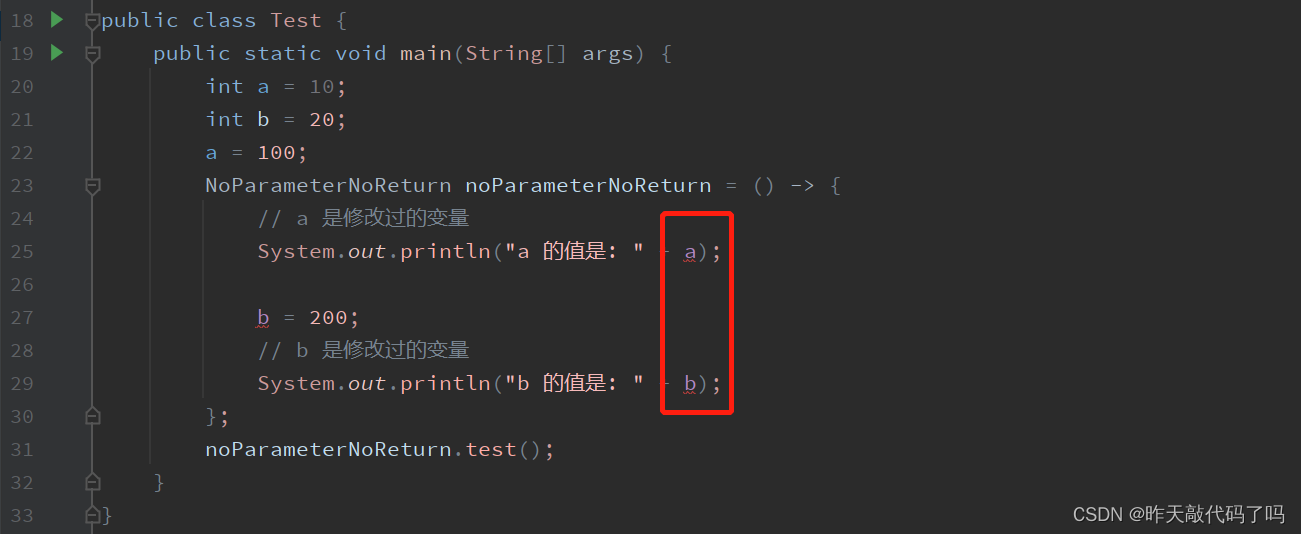
Java【lambda表达式】语法及使用方式介绍
相关文章目录 第一篇: Java【EE初阶】进程相关知识 进程管理 内存管理 文章目录相关文章目录前言一、lambda表达式 是什么?1, lambda表达式 的背景2, 什么是 函数式接口3, lambda表达式 的语法二、lambda表达式 的使用方式1, 无参无返回值2, 有一个参…...
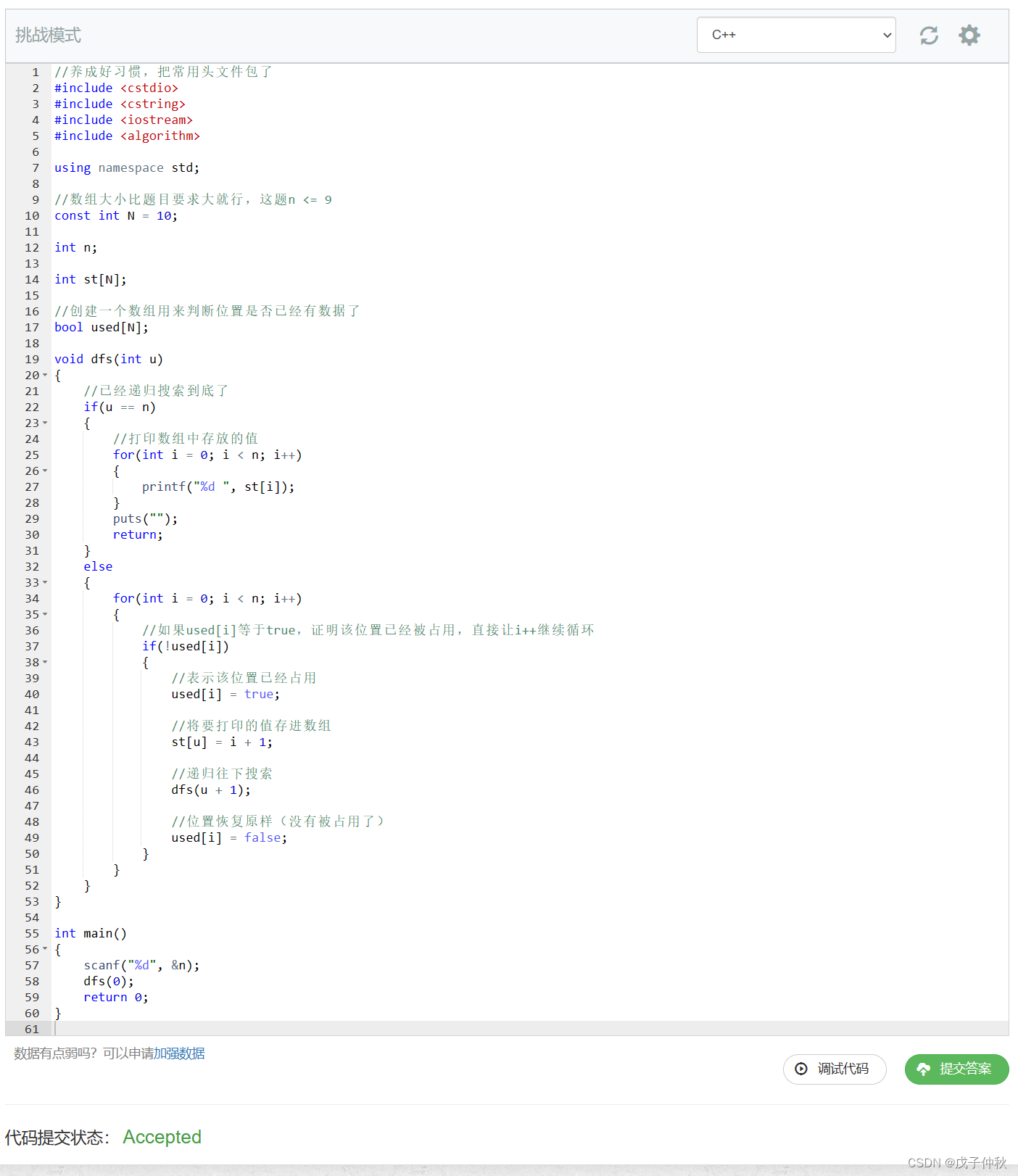
【AcWing】蓝桥杯备赛-深度优先搜索-dfs(2)
目录 写在前面: 题目:94. 递归实现排列型枚举 - AcWing题库 读题: 输入格式: 输出格式: 数据范围: 输入样例: 输出样例: 解题思路: 代码: AC &…...

‘conda‘不是内部或外部命令,也不是可运行的程序或批处理文件。
Anaconda环境搭建常见问题 conda不是内部或外部命令,也不是可运行的程序或批处理文件。 解决方案:配置环境变量 1.找到Anaconda Nvaigator单机右键 2.更多 3.打开文件所在位置 4.继续Anaconda Nvaigator单机右键,更多,选择文件…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...
